组合荷载作用下基桩水平承载特性的简化半解析解

饶文昌， 竺明星

(1.江苏开放大学 建筑工程学院， 江苏 南京 210019； 2.江苏科技大学 土木工程与建筑学院)

1 前言

随着工程需求的变化以及基桩承载特性理论研究的逐步深入，现实工程中的桩基通常不但承担桩顶竖向荷载作用，还同时受到水平荷载作用，即组合荷载的作用，如桥梁桩基础，海上风机单桩基础等。当桩身产生水平挠曲变形时，由于竖向荷载的存在会对桩身产生不利影响的附加弯矩，即p-Δ效应，这类问题引起了越来越多的学者关注。

对于组合作用下基桩承载机理，目前已有许多学者开展了相关的试验研究、数值分析和理论研究工作。Anagnostopoulos与Georgiadis、皇甫明等、梁发云等均开展了竖向荷载对水平受荷桩影响的室内模型试验。试验结果均表明：竖向荷载的存在对水平受荷桩的桩身弯矩有一定的影响，但不大；赵明华与吴鸣等开展了轴、横向荷载下桥梁基桩的试验研究，结果表明：在基桩自由长度和轴向荷载较大时，由于p-Δ效应，桩身最大弯矩和桩顶位移提高很大，在设计计算中不容忽视；Achmus等采用三维有限元分析了组合荷载作用单桩承载特性，研究结果表明：竖向荷载对水平受荷桩影响很小；Poulos、梁发云等根据弹性地基梁模型建立了组合受荷桩承载特性的解析模型并采用有限单元法进行求解，计算表明：轴向荷载的存在对于柔性桩上部的内力和侧向挠曲影响比较显著，而对其深部的影响相对较小，且认为轴向力作为常量的假设一般可以满足工程实际要求；赵明华等采用有限层单元法和改进有限杆单元法分析了倾斜荷载作用下基桩受力特性并指出p-Δ效应受多种因素影响且不容忽略；Zhu等根据传递矩阵法求得组合荷载作用下基桩桩身响应半解析解并得出p-Δ效应受桩的嵌入比影响显著的结论。

该文基于传递矩阵原理，采用Laplace正逆变换方法推导出简化的组合荷载作用下桩身传递矩阵系数，并通过迭代求解得出桩身响应。通过案例对比分析验证该文方法和解的正确性。最后开展竖向荷载对水平受荷桩承载特性影响分析。

2 桩身响应模型建立与求解

2.1 桩身受力模型

如图1所示，总桩长为L的基桩垂直嵌入到成层地基土中。地面上桩长为La，地面下桩长为Lb。地面上桩因等直变截面被等分为na段，则等分后每段桩的长度、桩径和抗弯刚度分别为Hai、dai和EIai。地面下的桩被成层地基土和等直变截面分成nb层，则每段桩的桩长、桩径和抗弯刚度分别为Hbi、dbi和EIbi；桩顶分别作用竖向荷载Vt、水平荷载Ft和弯矩荷载Mt；桩侧受到分布荷载qa的作用。推导过程中桩身变形y以向右为正，转角θ以逆时针旋转为正；桩顶水平力Ft与桩身截面剪力Q以绕研究对象顺时针旋转为正；桩顶弯矩Mt与桩身截面弯矩M以研究对象右侧受压为正；地面上桩侧分布荷载qa以向右作用为正；桩侧土抗力以向左为正。

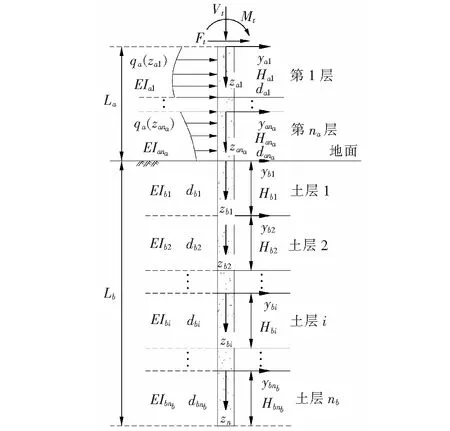
图1 成层地基土中桩身受力分析

2.2 地面上桩身传递矩阵系数求解

2.2.1 地面上任意截面处桩身受力模型

取地面上桩任意深度处微单元进行受力分析，如图2所示，图中所有物理量的符号均为正。

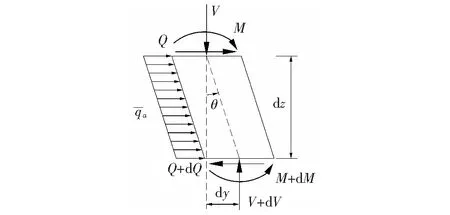
图2 地面上桩微单元受力分析

根据图2中桩身微单元水平方向受力平衡得：

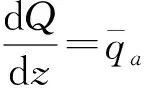
(1)

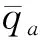
根据桩身微单元弯矩平衡可得：

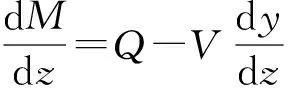
(2)

从图2可知：桩身轴力荷载会产生一个附加弯矩Vdy作用；同时由于θ=dy/dz，因此令：

Mva=Vθ

(3)

式中：Mva定义为竖向荷载引起的附加弯矩，单位量纲为[力×长度/长度]，其物理含义为沿桩身深度分布的单位长度附加弯矩作用。

将式(3)代入式(2)可得：

(4)

2.2.2 地面上任意深度处桩身传递矩阵系数求解

如图3所示为地面上自由段桩离散示意图。

图3 地面上桩离散示意图

采用Laplace正逆变换方法推导地面上桩身传递矩阵系数，根据图3建立如下微分方程组：

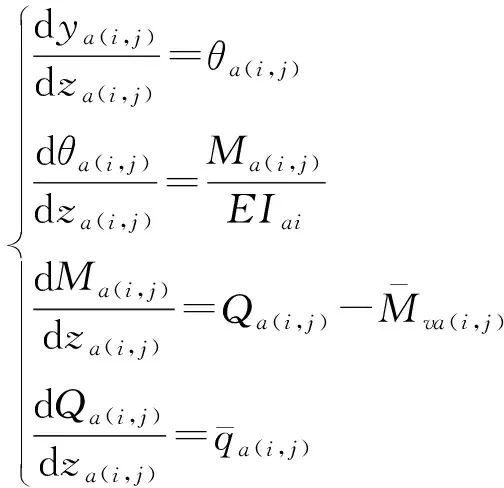
(5)

式中：ya(i,j)、θa(i,j)、Ma(i,j)和Qa(i,j)分别为第i层桩(根据直径进行分层)中第j小段桩(等分数量为mai)的桩端位移、转角、弯矩和剪力，如图3所示。

(6)

式中：qa(i,j-1)和qa(i,j)分别为第i层桩中第j小段桩的顶部与底部位置处分布荷载。

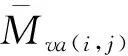
(7)

式中：Mva(i,j-1)和Mva(i,j)分别为第i层桩中第j小段桩的顶部与底部位置处附加弯矩。

Mva(i,j)采用下式进行计算：

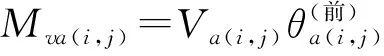
(8)

式中：Va(i,j)为第i层桩中第j小段桩的底部位置处桩身轴向荷载。赵明华、文献[13,15]均假定地面上桩身轴力因桩体自重随深度呈线性变化，则得：

(9)

式中：za(i,j)为从第i层桩顶至第j小段桩段的深度；ψai(=γaiAsai)为地面上第i层桩的桩身轴力增长系数，γai和Asai分别为地面上第i层桩的桩有效重度与横截面面积；ψak为地面上第k层(k=1，…，i-1)桩的桩身轴力增长系数；Hak为等分后地面上第k层(k=1,…，i-1)桩的长度。

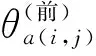
根据文献[13,15]对公式(5)进行Laplace正逆变换后可得：

Sa(i,j)=Ua(i,j)Sa(i,j-1)

(10)

式中：Ua(i,j)为地面上第i层桩中第j小段桩的桩身传递矩阵系数，如式(11)所示：

Ua(i,j)=

(11)

式中：hai(=Hai/mai)为地面上长度为Hai的第i层桩经过等分数量为mai等分后每小段长度；Sa(i,j)和Sa(i,j-1)分别为：

(12a)

Sa(i,j-1)=[ya(i,j-1)θa(i,j-1)Ma(i,j-1)Qa(i,j-1)1]T

(12b)

通过与文献[13,15]对比发现：该文式(11)的形式非常简洁；更重要的是该文解克服了文献[13,15]中自由段桩身传递矩阵系数轴力不能为0的局限性。因此，该文式(11)的解更具有实用性。

2.3 地面下弹性段桩身传递矩阵系数求解

2.3.1 弹性段范围内任意截面处桩身受力模型

取地面下桩土相互作用处于弹性阶段范围内的桩任意深度处一微单元进行受力分析，如图4所示，图中所有物理量的符号均为正。

根据图4中桩身微单元水平方向受力平衡得：

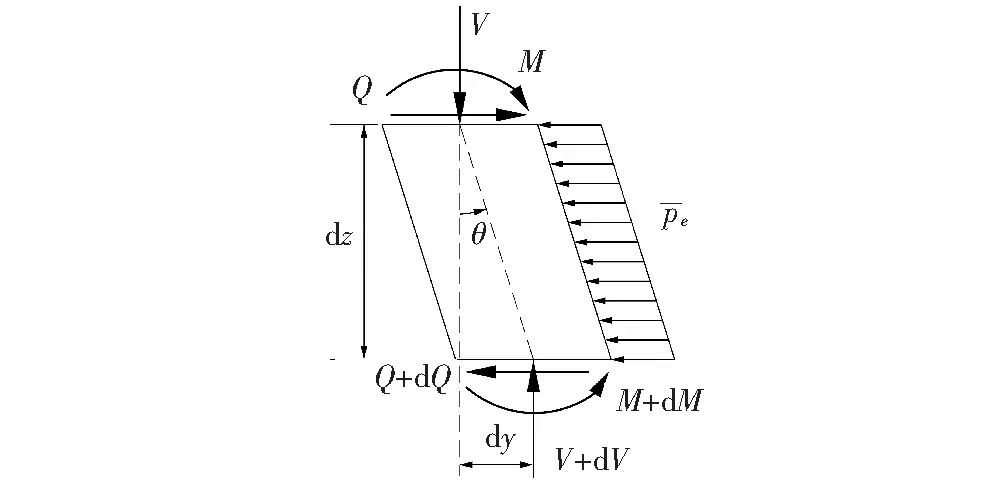
图4 弹性段桩微单元受力分析

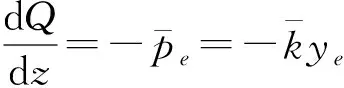
(13)

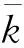
根据桩身微单元弯矩平衡可得：

(14)

式中：Mve为竖向荷载引起的弹性范围内桩身附加弯矩作用。

2.3.2 弹性段桩身传递矩阵系数求解

如图5所示为地面下弹性段桩离散示意图。

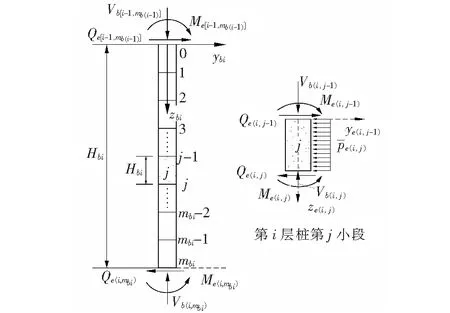
图5 地面下弹性阶段桩离散示意图

为采用Laplace正逆变换方法推导弹性段桩身传递矩阵系数，建立如下微分方程组：

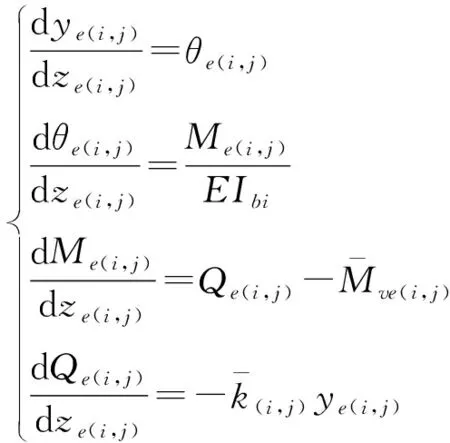
(15)

式中：ye(i,j)、θe(i,j)、Me(i,j)和Qe(i,j)分别为处于弹性阶段的第i层桩中第j小段桩(等分数量为mbi)的桩端位移、转角、弯矩和剪力(图5)。

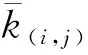
(16)

式中：k(i,j-1)和k(i,j)分别为第i层桩中第j小段桩的顶部与底部位置处土抗力模量。

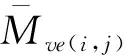
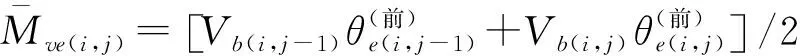
(17)

式中：Vb(i,j)为第i层桩中第j小段桩的底部位置处桩身轴向荷载。文献[13,15,17]均假定地面上桩身轴力因桩体自重和桩侧摩阻力随深度呈线性变化，则得：

(18)

式中：ze(i,j)为从第i层桩顶至第j小段桩段的深度；ψbi为地面下第i层桩的桩身轴力增长系数，采用如下公式计算：

ψbi=γbiAsbi-μτmax/2

(19)

式中：γbi和Asbi分别为地面下第i层桩的有效重度与横截面面积；μ为桩身横截面周长；τmax为第i层桩-土极限侧摩阻力。需要注意的是：如果式(17)计算所得桩身轴力Vb(i,j)小于0，则取Vb(i,j)=0。

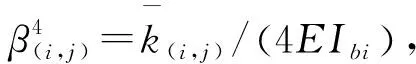
Se(i,j)=Ue(i,j)Se(i,j-1)

(20)

式中:Ue(i,j)为地面下第i层桩中第j小段桩(处于弹性阶段)的桩身传递矩阵系数，如下式所示：

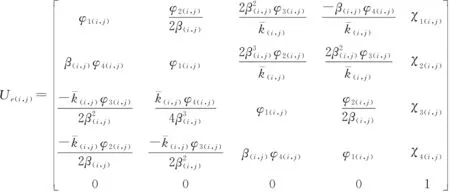
(21)

其中χ1(i,j)、χ2(i,j)、χ3(i,j)和χ4(i,j)分别为：

(22)

上述两式中：φ1(i,j)、φ2(i,j)、φ3(i,j)以及φ4(i,j)分别为：

(23)

其中：t(i,j)=β(i,j)hbi；hbi(=Hbi/mbi)为地面下第i层长度为Hbi的桩经过mbi数量等分后每小段长度。Se(i,j)和Se(i,j-1)扩充为5阶向量后如下所示：

(24a)

Se(i,j-1)=

[ye(i,j-1)θe(i,j-1)Me(i,j-1)Qe(i,j-1)1]T

(24b)

通过与文献[13,15]对比发现：该文式(21)～(23)极大地简化了考虑轴力作用时弹性段传递矩阵系数解的形式；更克服了文献[13,15]中弹性段传递矩阵系数轴力不能等于0的局限性。因此，该文式(21)、(22)的解更具有通用性。

2.4 地面下塑性段桩身传递矩阵系数求解

2.4.1 塑性段范围内任意截面处桩身受力模型

取地面下桩土相互作用处于塑性阶段范围内的桩任意深度处一微单元进行受力分析，如图6所示，图中所有物理量的符号均为正。

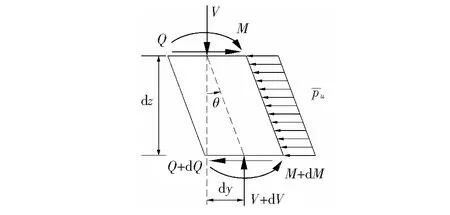
图6 塑性段桩微单元受力分析

根据图6中桩身微单元水平方向受力平衡得：

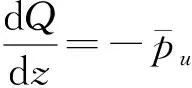
(25)

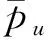
根据桩身微单元弯矩平衡可得：

(26)

式中：Mvp为竖向荷载引起的塑性范围内桩身附加弯矩作用。

2.4.2 塑性段桩身传递矩阵系数求解

如图7所示为地面下塑性段桩离散示意图。

根据图7建立如下微分方程组：

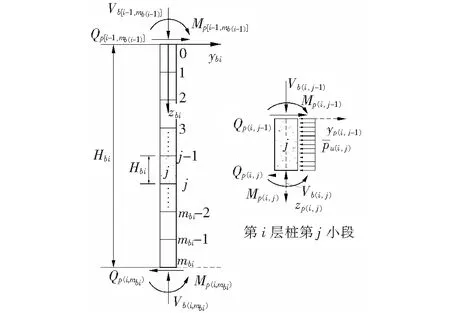
图7 地面下塑性阶段桩离散示意图

(27)

式中：yp(i,j)、θp(i,j)、Mp(i,j)和Qp(i,j)分别为处于塑性阶段的第i层桩中第j小段桩(等分数量为mbi)的桩端位移、转角、弯矩和剪力。

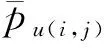
(28)

式中：pu(i,j-1)和pu(i,j)分别为第i层桩中第j小段桩的顶部与底部位置处极限土抗力值。

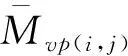
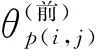
根据文献[13、15]对公式(27)进行Laplace正逆变换后可得：

Sp(i,j)=Up(i,j)Sp(i,j-1)

(29)

式中：Up(i,j)为地面下第i层桩中第j小段桩(处于塑性阶段)的桩身传递矩阵系数，如下式所示：

Up(i,j)=

(30)

Sp(i,j)和Sp(i,j-1)为扩充为5阶向量后如下所示：

(31a)

Sp(i,j-1)=

[yp(i,j-1)θp(i,j-1)Mp(i,j-1)Qp(i,j-1)1]T

(31b)

通过与文献[13,15]对比发现：该文式(30)不但表达方式简洁，更克服了文献[13,15]中塑性段传递矩阵系数轴力不能等于0的局限性。因此，该文式(30)所示塑性阶段传递矩阵系数更具有通用性。

2.5 组合荷载作用下桩身响应求解

在传递矩阵法原理的基础上，根据该文所求解的传递矩阵系数[式(11)、(21)以及(30)]可得整个桩身的传递矩阵方程：

Sb=Ub(nb,mbn)Ub(nb,mbn-1)…Ub(i,j)…Ub(1,1)×Ua(na,man)Ua(na,man-1)…Ua(i,j)…Ua(1,1)S0=US0

(32)

式中：Sb=[ybθbMbQb1]T和S0=[y0θ0M0Q01]T分别为桩端和桩顶处的变形、转角、弯矩和剪力的状态矩阵向量。Ub(i,j)为地面下第i层地基土中第j小段桩的传递矩阵系数，当该段桩土相互作用为弹性阶段时则采用式(21)计算，当该段桩土相互作用为塑性阶段时则采用式(30)计算；Ua(i,j)为地面上第i层桩中第j小段桩的传递矩阵系数，采用式(11)进行计算。Ub称为地面下桩的总传递矩阵系数，其值为从桩端至地面处的每小段桩身传递矩阵系数连续乘积；Ua称为地面上桩的总传递矩阵系数，其值为从地面处至桩顶的每小段桩身传递矩阵系数连续乘积；U(=UbUa)称为桩身总传递矩阵系数，其值为从桩端至桩顶的每小段桩身传递矩阵系数连续乘积。

方程(32)本质上是一个含有8个未知量(桩顶和桩端的变形、转角、弯矩和剪力)的方程组。为解得方程(32)，需引入桩顶、桩端的边界条件。常见的边界约束条件主要有自由、铰接和嵌固，因此可得如下桩顶和桩端初始边界条件：

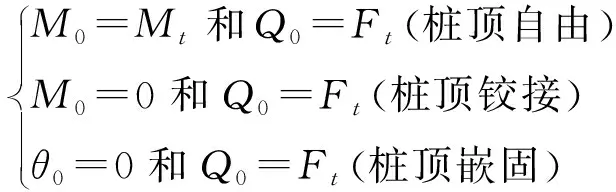
(33)

(34)

根据桩顶、桩端边界条件情况，将式(33)和(34)中对应的值代入方程(32)即可解得桩顶处的变形、转角、弯矩和剪力的状态矩阵向量S0，则地面上任意位置处的桩身响应为：

Sa(i,j)=Ua(i,j)Ua(i,j-1)…Ua(1,1)S0

(35)

地面下任意位置处的桩身变形、转角、弯矩和剪力值为：

Sb(i,j)=Ub(i,j)Ub(i,j-1)…Ub(1,1)UaS0

(36)

3 案例验证与轴力影响分析

3.1 案例验证

吴鸣与赵明华开展了组合荷载作用下模型桩承载特性试验。桩长L=0.8 m，桩外径d=0.016 m，壁厚t=0.002 m，抗弯刚度EI=0.189 kN·m2。文献[13]采用如下桩土相互作用p-y曲线模型进行分析：

(37)

式中：nhs(=5.84×103kN/m3)为土抗力系数值；z0(=0.3 m)为等效深度；m(=0.8)为指数系数；yu(=3d/80=6×10-4m)为塑性位移。桩顶、桩端均为自由边界。该文取桩身轴力为等于桩顶竖向荷载的一个常量值，则地面下桩身弯矩理论计算值与实测值对比如图8所示。

由图8可知：该文方法所得解与文献[13]所得解完全一致，证明了该文简化思路和推导过程的正确性；同时，该文解与文献[7]中的有限层单元解和实测值结果均非常接近，说明了该文解的合理性和有效性。

图8 桩身弯矩计算值与实测值对比

3.2 桩身轴力对水平承载力影响的参数分析

Han认为地面上自由段桩长对组合荷载作用下基桩水平承载特性有显著的影响，并引入嵌入比概念开展桩身轴力对水平承载力的影响分析。嵌入比，即嵌入地基土中的桩长(Lb)与整个桩长(L)的比值(Lb/L)。该文以上述案例验证中的桩为模型，假定嵌入比Lb/L分别为0.6、0.7、0.8、0.9、1.0。桩顶水平荷载为Ft=0.15 kN，桩顶竖向荷载Vt分别为0Ft、0.5Ft、1.0Ft、1.5Ft和2.0Ft。则桩顶最大变形计算结果如图9所示。从图9可知：不同桩顶竖向荷载作用下，桩顶最大变形随嵌入比Lb/L的变化规律相同，即桩顶变形均随着嵌入比的增加而减小。相同嵌入比情况下，桩顶变形随着桩顶竖向荷载的增加而增加；但是当嵌入比Lb/L为0.9～1.0时，桩顶水平变形非常接近，几乎不受桩顶竖向荷载作用的影响。

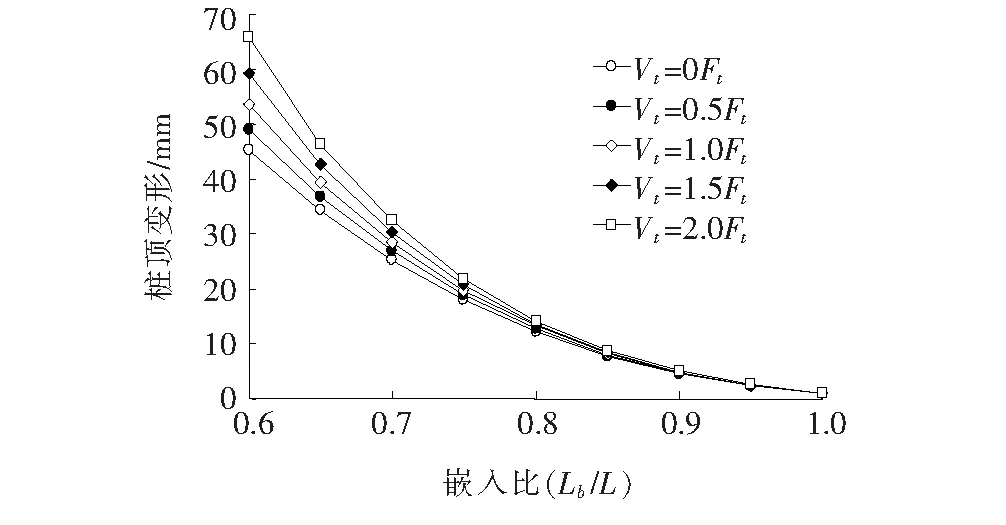
图9 桩顶竖向荷载及嵌入比对桩顶变形的影响

嵌入比Lb/L对桩身附加弯矩的影响如图10所示。如果附加弯矩为负值，则表明该附加弯矩的作用方向与桩身截面弯矩正方向一致，对桩受力而言是不利的；如果附加弯矩为正值，则对桩受力是有利的。从图10可明显得出：在恒定桩顶竖向荷载作用时(Vt=1.0Ft)，桩身附加弯矩随着嵌入比Lb/L的减小而显著增加，这说明p-Δ效应随着地面上自由段桩长增加而逐渐明显。尽管在接近桩端处附加弯矩为正值，但与负值的附加弯矩相比可以忽略。

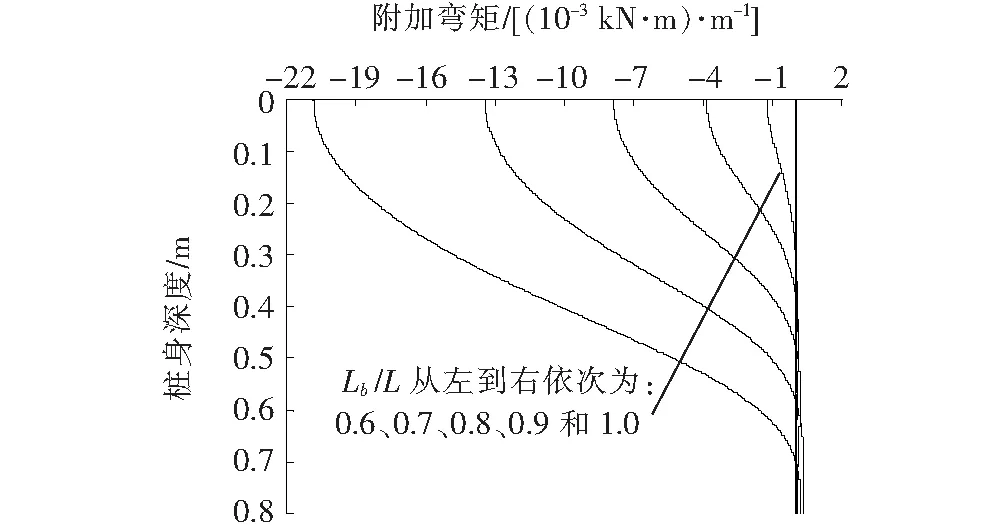
图10 嵌入比对附加弯矩的影响(Vt=1.0Ft)

图11为桩身轴力对附加弯矩的影响(Lb/L=0.7)。从图11可知：在恒定嵌入比时，桩身附加弯矩值随着桩顶竖向荷载的增加而显著增加。综合图9～11可知：当嵌入比Lb/L较小时，如果桩顶存在竖向荷载作用，则需要考虑p-Δ效应对桩水平承载力的影响。

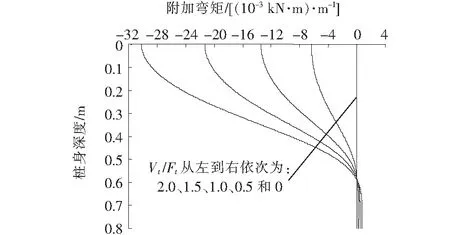
图11 轴力对附加弯矩的影响(Lb/L=0.7)

4 结论

为研究竖向荷载对水平受荷桩承载特性的影响，引入附加弯矩概念并建立任意截面处桩身轴力作用引起的附加弯矩计算表达式。在传递矩阵法原理的基础上，通过Laplace正逆变换解得地面上自由段桩、地面下弹性段以及塑性段桩的传递矩阵系数解析解，并通过迭代求解得出桩身响应。通过案例对比分析验证了该文方法和解的正确性。与既有文献半解析解相比，该文解的形式更加简洁，且克服了既有文献方法中传递矩阵系数轴力不能为0的缺陷。最后该文开展了竖向荷载对水平受荷桩承载特性参数影响分析，得出以下结论：

(1) 桩顶变形随着嵌入比的增加而减小；相同嵌入比情况下，桩顶变形随着桩顶竖向荷载的增加而增加；但当嵌入比Lb/L为0.9～1.0时，桩顶水平变形几乎不受桩顶竖向荷载作用的影响。

(2) 在恒定桩顶竖向荷载作用时，桩身附加弯矩随着嵌入比Lb/L的减小而显著增加，这说明p-Δ效应随着地面上自由段桩长增加而逐渐明显。

(3) 在恒定嵌入比时，桩身附加弯矩值随着桩顶竖向荷载的增加而显著增加。

(4) 当嵌入比Lb/L较小时，如果桩顶存在竖向荷载作用，则需要考虑p-Δ效应对桩水平承载力的不利影响。