基于CEEMD和SVD的路面纹理与抗滑性能研究
2022-01-12彭慧婷呙润华司有强
彭慧婷 呙润华 徐 粒 司有强
(新疆大学建筑工程学院1) 乌鲁木齐 830046) (清华大学土木工程系2) 北京 100084)
0 引 言
抗滑性能是衡量路面安全性能的主要评价指标.其测量方法主要是传统的接触式方法如摆式摩擦仪等.英国道路运输研究所发明了摆式摩擦系数测定仪,最早是用于评价路面抗滑性能的切实可行的方法和标准.Fwa等[1]采用Abaqus模拟摆式摩擦仪测定过程,发现该数值模拟可以较好地模拟实际测量过程中摩擦块滑移的长度、摆值的大小,与真实测试结果相吻合.随着计算机技术的发展,非接触式检测技术逐渐发展起来,激光技术和相机拍照技术在路面上逐渐应用起来.Zahouani等[2]应用激光跟踪聚焦方法测试了沥青路面纹理形貌,提取出了路面微观纹理形貌,但该方法仅用于二维形貌轮廓的测量.通过激光三角法原理设备可以对车辙深度、平整度以及宏观纹理等重构表面形貌[3].Fang等[4]采用矩阵实验室算法对单颗集料图像进行处理和傅里叶分析发现基于傅里叶函数的矩阵实验室算法结果准确,并可用于表征集料的表面形态特征.
目前,常用的路面抗滑性能评价指标主要有基于摩擦系数指标(british pendulum number,BPN)、纹理分形维数(D)、平均构造深度(mean texture depth,MTD)和平均断面深度(mean profile depth,MPD)等.大量学者通过考察纹理指标与道路摩擦系数间的相关性,建立预测模型[5-6].Chou等[7]在现有的MPD和MTD的基础上提出一种新的基于激光技术的评价指标(mean difference of elevation,MDE),MDE为测量长度上每两个相邻点间距固定的高差之和除以测量长度上的点个数.Meegoda等[8]研究摩擦系数与MPD值间的关系,研究发现MPD值分布不同与摩擦系数具有正负相关性,在此基础上研究纹理构造深度与胎路接触面积,水膜厚度等与摩擦系数间的关系.周兴林等[9]基于分形理论,研究不同磨光状态下路面纹理的分形特征,提出截止波长概念作为评价普通磨光和差异磨光的指标,水平截止波长表示平均微凸体尺寸,垂直截止波长表示骨料的平均高度,应用三维激光扫描仪,提取不同磨光纹理信息.杨国峰等[10]用多功能路况快速检测系统(CiCs)采集路面构造深度信息,计算路面磨耗率,对比分析无路面磨耗与有磨耗路面的MTD与MPD值,建立路面磨耗与路面纹理的平均构造深度之间的评价模型,并拟将该模型应用于纹理评价指标标准中.Rado等[11-12]提出利用希尔伯特-黄变换对二维纹理信号进行处理,通过希尔伯特变换得到联合固有模态函数BIMF的瞬时频率和瞬时振幅,提取峰值包络线并求均值研究与摩擦系数间的相关性.
文中通过三维激光断面仪获取不同车辙板样本的表面信息,针对表面高程数据特点引入了一种新的路面纹理采集滤波方法,提出了新的抗滑评定指标σi(纹理抗滑参数),该指标与摆值BPN呈现良好的相关性,可作为未来非接触式抗滑评定参考.
1 基本原理
1.1 三维激光断面仪工作原理
三维激光断面仪见图1.该设备由高速三维相机、线激光发射器、轴编码器DMI、千兆网信号传输线、控制中心组成,脉冲激光以线形呈现在靶材上,长270 mm,相机调查宽度为2 048 mm,意味着激光分散到像素点间距为0.12 mm.其总体布置架构见图2,通过高速3D相机捕捉激光线,随着靶材高度变化,表面激光亮条纹在相机网格阵中与原来的位置发生相对移动,激光条纹与背景存在明显强度差,采用门限处理将其与背景进行二值化,通过重心算法[13](获取激光条纹中心)和数字图像滤波技术计算出每个目标点与预设零位面之间的距离,从而得到线激光扫描过的道面三维高程信息.

图1 三维激光断面仪
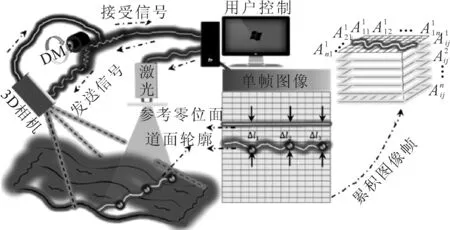
图2 三维激光断面仪架构示意图
在实际的采集过程中,高速3D相机图像帧采集模式分为静态模式和距离触发模式,静态模式由控制中心发出采集信号,该模式通常在室内模拟不同速度采集状况,距离触发模式由数字轴编码器DMI(固定于车轮轴)触发采集信号.
1.2 CEEMD原理
激光扫描仪采集的三维纹理数据包含了丰富的表面高程信息.它由300列二维非线性非平稳信号组成,包括各种噪声干扰和多频混合信号.对于这种类型的数据处理,Huang等[14-15]提出EMD(empirical mode decomposition)算法,将原始信号s(t)分解为n个固有模态函数IMF和一个余项.
(1)
式中:IMFi(t)为固有模态函数;rn(t)为余项.
由于EMD算法存在严重的模态混叠现象,对原始信号的重构较差,因此Wu等[16]提出改进的EEMD算法(ensemble empirical mode decomposition).EEMD通过向原始信号中不断添加高斯白噪声消除EMD存在的模态混叠现象,
(2)
式中:N为添加的白噪声个数;Ci,j(t)为添加第j个白噪声处理后第i个IMF.EEMD由于添加白噪声,在信号处理过程中不能完全的消除,影响信号的纯度.
补充集合经验模态分解(CEEMD)[17]是一种基于EEMD的优化算法,能够有效克服模态混叠和白噪声干扰,并对信号实现精确地重构.主要通过在原信号中加入N个正、负辅助白噪声,得到2N个信号,对每个信号进行EMD分解,最后将计算结果进行组合.CEEMD过程与EEMD相同,不同之处在于在添加噪声之后添加相反符号的噪声,按照EMD分解得到IMFs.
1.3 奇异值分解原理
奇异值分解(SVD)是一种重要的矩阵分解方法.实际生活中,大多数矩阵都不是方阵,特征值分解一般只适用于方阵,而奇异值分解可以应用于任何矩阵的分解.奇异值分解是主成分分析的主要步骤,通过提取主成分将复杂的大数据矩阵简化为低维数据矩阵.假设C为m×n阶矩阵.
C=UΣVT
(3)
式中:U为m×m阶酉矩阵;Σ为半正定m×n阶对角矩阵;VT为V的转置矩阵,是n×n阶酉矩阵.这样的分解就称作C的奇异值分解.Σ对角线上的元素δi即为C的奇异值.通常分解后的奇异值按照由大到小的顺序排列,δ1>δ2>δ3>…>δi(1 在热拌沥青(HMA)试块表面共选取了8个300 mm×300 mm的试验区域,利用激光线匀速扫描测试表面,三维纹理中的任一界面高程曲线见图3a),运动过程中获得的累积图像帧见图3b),该过程将获取测试区域的原始纹理信息.其次为了与英国摆式摩擦仪的测试区域相同,取中心面积为100 mm×100 mm的中心区域作为测试对象,激光传感器采集到的相应数据为800×300矩阵,实际操作过程中获取得到的原始高程信息还包含有噪声值(利群异常值),因此将原始数据通过上述CEEMD原理进行滤波处理,并对其表面高程数据进行三维重构得到图3c)效果,依次将所有样本表面100×100数据进行奇异值分解得到σi.最后采用英国摆式摩擦仪测量了表面的抗滑性见图3d),并记录了5次摆测值及其平均值,摆值的大小根据温度变化进行了修正. 图3 实验采集流程 将300列原始数据中的每一列二维原始信号进行CEEMD分解,在图4中,将固有模态函数个数设置为8,分解后得到9个IMFs和一个余项Rs10,其中IMF1为原始信号,IMF2~IMF9分别为原信号的单一模态分解函数.其次把各IMF按照频率由大到小依次排列,高频部分包含部分微观和宏观纹理信息.IMF6及以上为低频信号,具有大量纹理信息,余项代表信号变化趋势和信号分解的稳定程度.将原始信号和余项去掉,对IMF2~IMF9组成的800×8矩阵利用式(4)进行奇异值分解,得到奇异值矩阵Σ800×8,并提取每一列的非零奇异值向量,见图4. 图4 CEEMD分解IMF函数及余项 (4) 接着将300原始数据中每列的奇异值分别求和式(5),式中σij为300列原始数据的第j列经奇异值分解的第i行奇异值;σi为300列数据第i行奇异值的总和. (5) 此次试验中,对每个试件的300列二维信号进行CEEMD分解.一个800×8矩阵由8个IMF组成,用于奇异值分解,每次分解后提取并累积奇异值.表1为基于八组测试区域数据的回归分析,并与通过摆式摩擦仪测量的摆值进行线性拟合.结果表明σ1~σ5与路面摩擦系数R2拟合优度大于0.8,具有良好的线性相关性;σ6~σ8的R2拟合优度小于0.6,拟合较差.其中σ3与摆值的R2拟合优度最高为0.877,拟合直线如图5. 表1 σi和BPN的相关性 图5 σ3与BPN线性拟合方程 拟合方程为 y=0.007 8x+34 (6) 为了进一步验证σi参数的可靠性,对采集数据进行了轮廓算术平均偏差Ra的计算,来验证σi与抗滑性能的相关性.Ra为轮廓偏差绝对值在采样范围内的算术平均值.从统计学意义上讲,它是以路面表面纹理高程形貌大小分布取其平均,反映了地形的轮廓振值相对于基准线的离散程度,被广泛用于评价表面形貌特征的粗糙程度.其计算式为 (7) 式中:z(x,y)为基于基准线的形貌高程数据;M,N为相互垂直的两个方向上的采样点数. 通过对三维纹理数据进行计算,并与测量的摆值和σi进行线性拟合.在表2中,可以明显的观察到,σ1~σ5与轮廓算术平均偏差Ra拟合优度超过0.9,具有非常良好的线性相关性,其中σ1达到最高的相关性为0.944;而σ6~σ8的R2拟合较差.最后,Ra与BPN的拟合优度为0.772.其拟合直线见图6,式(8)~式(9)分别为σ1与Ra、BPN与Ra的线性拟合方程 图6 σi、BPN与Ra线性拟合方程 表2 σi、BPN和Ra的相关性 Yσ1=0.69x-0.11 (8) YBPN=0.26x+0.33 (9) 起初,将CEEMD分解时设定分解个数为8.由图7可知,当分解个数大于8时,IMF9与IMF10函数变化趋势一致,只是分解频率降低;当分解个数小于8时,原始信号分解不充分,无法完全提取原始信号的特征信息.当改变固有模态函数IMF分解个数时,即当IMF个数大于8时,分解后的σi与摆值的拟合度在i≤5时具有良好的相关性,与IMF等于8时相同;当IMF个数设置小于8时,每次分解的最后两项σx(i-2≤x≤i)与摆值的拟合度较差,而σx(x≤i-2)与摆值的拟合度均大于0.8.由此说明当IMF分解个数大于8时,σ1~σ5对于不同个数IMF与纹理摩擦值都具有良好的相关性;当IMF分解个数小于8时,σi与摆值的拟合度大于0.8的个数逐渐减少. 图7 R2大于0.8的个数与IMF分解次数的对比 综上所述,路面纹理信号具有复杂性,线激光传感器可以从空间域直接采集纹理信息.在本研究中,将复杂的原始信号,利用CEEMD和SVD分解为单一模态函数和奇异值向量.通过对奇异值求和,得到纹理抗滑参数σi,并发现其与路面摩擦值具有很好的相关性.通过底部非接触式纹理采集模块收集丰富的路面三维纹理信息,通过计算σi可以快速获得抗滑性能指标. 1) 通过三维激光构造仪获取车辙板二维和三维纹理信息,通过CEEMD算法对二维原始信号进行分解得到800×10的矩阵;将IMF1和RS10去掉,对800×8的矩阵进行奇异值分解得到信号的特征值向量σij并对其求和得到σi. 2) 分别对σi与摆值进行线性拟合,σ1~σ5具有良好的相关性,拟合优度大于0.8.当IMF分解个数大于8时,σ1~σ5对于不同个数IMF与纹理摩擦值都具有良好的相关性.当IMF分解个数小于8时,σi与摆值的拟合度大于0.8的个数逐渐减少. 随着道路检测养护管理的发展,快速检测评价技术越来越重要.通过对σi与摩擦系数间的相关性分析,可以快速高效的为交通基础设施管理平台提供数据支持,为我国网级路面管理决策平台建设提供技术支持.2 实验方法

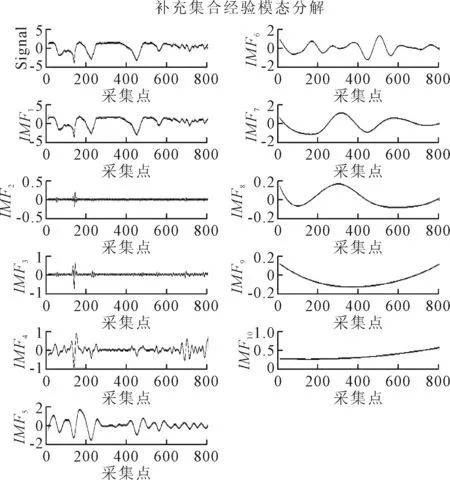
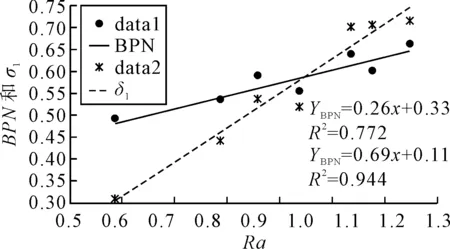
3 数据处理与讨论


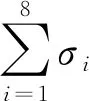

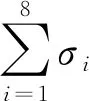
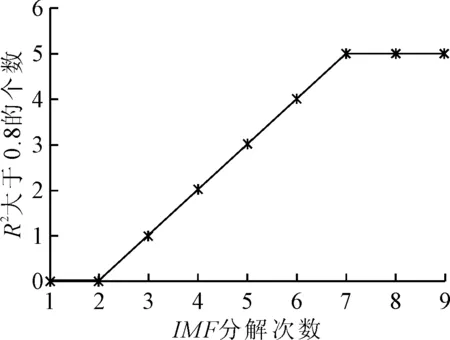
4 结 论
