基于LSTM神经网络的随机横浪中船舶横摇运动极短期预报

易文海 高志亮

(武汉理工大学船海和能源动力工程学院1) 武汉 430063) (高性能船舶技术教育部重点实验室2) 武汉 430063)

0 引 言

船舶运动极短期预报[1]是指对船舶未来几秒到十几秒的运动姿态进行预报，其有效实现有助于保障船舶在海上航行及作业安全.船舶运动极短期预报理论多种多样，已发展出自回归法[2]、卡尔曼滤波法[3]、周期图法[4]、支持向量机法[5]、人工神经网络法[6]等方法.

近年来，随着人工神经网络算法的蓬勃发展，越来越多的学者运用人工神经网络进行船舶运动极短期预报.刘婉婷[7]分别采用卡尔曼滤波法、径向基神经网络和Elman神经网络对船舶升沉运动进行预报，结果表明Elman神经网络有更好的预报精度.张泽国等[8]提出了一种自适应变异的粒子群优化算法与反向传播(back-propagation，BP)神经网络结合的组合模型，运用该模型对科研教学船“育鲲”轮的横摇运动数据进行实时预报，验证了该方法的可行性和有效性.Li等[9]通过BP神经网络对船舶横摇运动进行了预报，并与自回归滑动平均方法进行了比较分析，结果表明：BP神经网络有更好的预报精度.王国栋[10]用自回归模型、传统循环神经网络模型及长短期记忆(long short-term memory，LSTM)神经网络模型对实船横摇和纵摇运动数据做了预测分析，结果表明LSTM神经网络有更好的预报精度.Zhang等[11]通过组合卷积神经网络和LSTM神经网络对实验测得的横摇数据进行了预测研究，证明了方法的有效性.彭秀艳等[12]在LSTM神经网络算法上整合了粒子群算法和经验模态分解算法，结果表明该混合模型有效提高了预报精度.

目前，在运用人工神经网络进行船舶运动预报方面，大多学者均基于船舶自身摇荡运动历时数据进行建模，而通过波高历时数据进行船舶运动历时预报的研究报道甚少.实际上，船舶摇荡运动与波浪运动密切相关，为了验证利用波高历时数据预报船舶运动历时的可行性，文中基于Tensorflow平台构建LSTM神经网络模型，对基于随机横浪波高数据的船舶横摇运动极短期预报方法进行研究.

1 LSTM神经网络模型

1.1 LSTM神经网络原理

LSTM神经网络是一种特殊的循环神经网络，它首次由Hochreiter等[13]提出，它的出现有效解决了传统循环神经网络梯度爆炸问题，同时LSTM神经网络能够处理长时间序列数据，具有长时记忆能力.波浪与船舶摇荡运动存在着响应关系，故可采用LSTM神经网络建立波浪和船舶运动时间序列的映射关系，从而进行船舶运动姿态的预报.

LSTM单元结构由遗忘门、输入门、输出门和单元状态组成，具体数学模型见文献[14]，单元结构见图1.在当前t时刻，LSTM网络输入参数有三个：当前时刻输入值xt(如波高)、上一时刻输出值ht-1(如船舶运动)、上一时刻单元状态ct-1.输出参数有两个：当前时刻输出值ht和当前时刻单元状态ct.LSTM通过激活函数σ实现对三个门的控制，从而实现对历史信息的保留与遗忘.

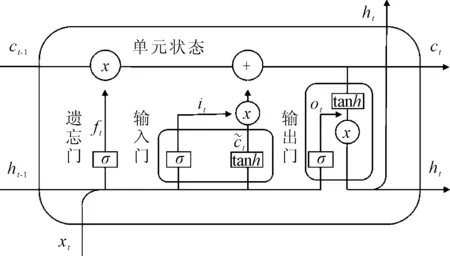
图1 LSTM单元结构图

1.2 基于LSTM神经网络船舶运动预报

LSTM神经网络预报模型流程主要有数据输入、数据预处理、LSTM模型参数设置、LSTM模型训练及预测、预测结果评估.

1.2.1船舶运动数据

通过基于势流理论的船舶水动力计算软件AQWA对DTMB5415舰船进行时域仿真，获得LSTM模型所需数据，船型参数见表1.首先将AQWA计算得到的横摇频率响应函数与试验测量结果[15]进行了对比验证，证明了AQWA计算结果的可靠性，见图2.接着通过AQWA时域计算模块得到零航速下DTMB5415在三、四、五级随机横浪下的入射波高历时数据以及船舶横摇运动历时数据，用于LSTM模型训练预报，海况参数见表2，数据的采样间隔为0.4 s，每组数据4 500个，总共时长1 800 s.

表1 DTMB5415船型参数

θ-横摇角幅值；K-波数；A-波幅；ω-波浪圆频率；L-船舶水线长；g-重力加速度

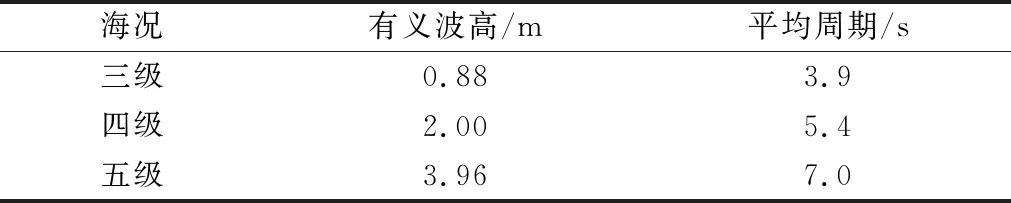
表2 海况参数

1.2.2数据预处理

对训练数据进行归一化处理，归一化数学表达如下.

(1)

式中：x*为归一化数据；x为原始数据；xmin和xmax分别为原始数据中最小值和最大值数据.

1.2.3LSTM模型参数

LSTM神经网络参数主要有输入步数、神经元节点数、隐藏层数、优化器类型及学习率、训练迭代轮数、训练批次大小等.其中有些参数设置不仅影响着模型训练效率，同时影响预报精度，所以需通过选取合适的模型参数，在保证预报精度的同时有效提高训练效率.

文中主要对输入步数对结果的影响进行分析.输入步数代表着输入数据的时间序列长度，它直接影响着预测结果的准确性.理论上输入步数越多，神经网络越能抓取时间序列数据的特征；但输入步数过多，LSTM神经网络可能会提取无用信息导致出现过拟合现象，影响预报精度，同时输入步数过大会导致计算量加大，增加训练时间，所以要选取合适的输入步数来保证预报精度和计算效率.

1.2.4LSTM模型训练及预测

分别建立基于波高历时数据和基于船舶自身横摇历时数据作为输入数据的LSTM模型，用于预报船舶横摇运动历时.假设波高时间序列数据为(h1，h2，…，ht)，船舶横摇角度数据为(θ1，θ2，…，θt)；在进行训练及预测时，对输入数据进行滑窗，组成输入向量组X，窗口长度为j(j小于t)，窗口长度即为输入步数.输出向量组Y为每个窗口对应的船舶横摇角度数据θj+n，其中:n为预测间隔步数，用来控制提前预报时长，提前预报时长为n乘以数据采样间隔.当n=0时，预测模型为用当前时刻及前一段时间的输入数据预测当前时刻的船舶横摇角度；当n>0时，预测模型为用当前时刻及前一段时间的波数据预测未来第n个数据时刻对应的船舶横摇角度.

1.2.5预测结果评估

预测结果采用最大绝对误差(maximum absolute error，MAE)和均方根误差(root mean square error，RMSE)方式来评判，其中最大绝对误差给出了预测过程中误差的最大值，均方根误差则体现了整体预测误差情况.MAE和RMSE数学表达如下.

MAE=max(|predictioni-labeli|)

(2)

(3)

式中：prediction为预测值；label为理论值.

2 LSTM模型验证结果及分析

LSTM模型主要参数设置如下：神经元节点数为16，隐藏层层数为2，优化器选择为Adam(adaptive moment estimation)，学习率设置为0.000 6，训练迭代轮数为30 000，训练批次大小为32.训练样本数为4 000个，时长为1 600 s.考虑到三、四、五级海况周期不同，测试样本数分别为100、150和200个，测试时长则分别为40、60、80 s.

2.1 输入步数影响分析

基于波高输入数据的LSTM模型，采用三、四、五级海况波高和船舶横摇角度数据，分析输入步数对模型预报精度的影响.预测间隔步数n为0，分别用50、100、200、300、400、500、600、700的输入步数代入模型进行预测分析，结果列于表3.

由表3可知，随着输入步数增加，均方根误差和最大绝对误差呈现出先减小后增大的趋势.对于三级海况，当输入步数取600时有最好的预报精度，其预测值基本与真实值相吻合，图3a)为三级海况输入步数为50、200、400、600的结果比较.对于四级和五级海况，当输入步数取500时有最好的预报精度，图3b)～c)分别给出了四级和五级海况输入步数为50、100、300、500的结果比较.上述比较结果表明，随着输入步数增加，LSTM神经网络能更有效捕捉数据规律特征；但输入步数过大，会导致LSTM神经网络提取无用信息进行数据拟合，从而导致预测精度有所下降.此外，相比于四级和五级海况，三级海况下船舶横摇角度较小，分析认为需要更长的输入步数来挖掘波高与船舶横摇数据间的内在联系.

表3 不同输入步数预报结果

图3 不同输入步数结果比较

2.2 两种模型预报结果对比分析

选取三、四、五级海况波高和船舶横摇角度作为研究数据，对基于波高输入数据的LSTM模型和基于横摇输入数据的LSTM模型在不同提前时长下的船舶横摇预报精度进行比较分析.两种模型采用相同的参数设置，三级海况输入步数为600，四级和五级海况输入步数为500.提前预报时长取2、4、6和8 s四种情况，所对应的预测间隔步数(n)分别为5、10、15、20.

表4～5分别汇总了两种模型得到的不同海况下船舶横摇预报精度，图4～7为船舶横摇理论值和预测值的历时对比.由表4～5可知:随着提前预报时长的增加，两种模型的预报精度都逐渐下降，这是因为随着提前预报时长增大，时间序列数据之间的相关性减弱，使得预报精度降低.在三级海况下，基于波高输入数据模型和基于横摇输入数据模型的均方根误差接近；对于最大绝对误差而言，当提前时长为6和8 s时，基于波高输入数据模型预报精度分别提升了11%和49%.在四级海况下，基于波高输入数据模型均方根误差和最大绝对误差均相比于基于横摇输入数据模型有所改善；当提前预报时长为6 s时，均方根误差和最大绝对误差分别下降了6%和7%；当提前预报时长为8 s时，均方根误差和最大绝对误差分别下降了19%和26%.在五级海况下，基于波高输入数据模型的预报精度有更大的提升；当提前预报时长为6 s时，均方根误差和最大绝对误差分别下降了58%和46%；当提前时长为8 s时，均方根误差降和最大绝对误差分别下降了44%和46%.

表4 不同提前预报时长预报结果(基于波高输入数据)

表5 不同提前预报时长预报结果(基于横摇输入数据)

图4 三级海况不同提前预报时长结果

图5 四级海况不同提前预报时长结果

图6 五级海况不同提前预报时长结果

图7 五级海况下两种模型结果对比图

总体而言，基于波高输入数据模型预报精度整体比基于横摇输入数据模型要好.分析认为基于横摇输入数据模型是通过挖掘自身数据规律特征进行预报，当样本量不够庞大时峰值点特征难以训练得到，进行峰值预报时结果往往不够准确.波浪是船舶摇荡运动的激励因素，基于波高输入数据模型是通过挖掘波高与船舶运动之间的响应关系，分别以波高和船舶横摇作为输入和输出，理论上能更有效地预报船舶横摇运动，故横摇角峰值点预报更加准确.此外，随着海况提高，波浪增大，波高与船舶运动之间有更强的响应关系，故在高海况下利用波高与船舶横摇角进行映射训练，能取得更好的预报结果.

3 结 论

1) 模型预报精度总体上随输入步数增加而提高，但当输入步数增加到一定值时，分析认为由于过拟合问题会使模型预报精度有所下降.

2) 对于不同提前时长预报，两种模型都呈现出随提前时长增加而预报精度下降的趋势，但随着海况的提高，在相同提前时长条件下，基于波高输入数据的LSTM模型能得到精度更高的结果.当提前预报时长为6和8 s时，与基于横摇输入数据的模型相比，基于波高输入数据模型在四级海况下预报精度可提高约5%和20%，而在五级海况下精度均可提高约50%.

由于本文通过线性势流理论得到的研究数据与真实情况下的波浪和船舶运动数据的特征还存在一定差别，后续将采用更为真实的数据对本文方法有效性进行验证.