基于准无限时域MPC的无人艇轨迹跟踪控制器

王 浩 董早鹏 刘 洋 张海胜 齐诗杰

(武汉理工大学船海与能源动力工程学院 武汉 430063)

0 引 言

水面无人艇(unmanned surface vehicle，USV)轨迹跟踪的定义是给定一条与时间相关的曲线，通过设计控制器算法使USV设定时间内跟踪到该轨迹的特定位置上.

准无限时域模型预测控制(model predictive control，MPC)因为能处理PID较难解决的多变量约束优化控制问题[1]，逐渐被采用在船舶运动控制领域.文献[2]提出了一种带有干扰观测器、基于非线性模型预测控制方法的欠驱动船舶路径跟踪控制器设计方法；文献[3]提出了一种基于模型预测控制的直线航迹跟踪的设计方法；文献[4]提出了一种基于LMI(linear matrix inequalities)的非线性模型预测控制方法，实现了对USV的镇定控制；文献[5]提出了基于线性模型预测控制的USV轨迹跟踪控制方法，但没有提出相对应的理论证明所设计控制器的稳定性.对于MPC的稳定性分析问题，文献[6]指出保证MPC的稳定性最直接的办法是采取无限时域；文献[7]提出了可以证明连续时间上准无限时域的模型预测控制的方法，解决了无限时域无法直接实现的问题；文献[8]提出加入终端惩罚函数，可以证明离散时间准无限时域的模型预测控制的稳定性方法,但是未曾在USV轨迹跟踪上有所应用.

根据以上研究得知：虽然MPC在USV的运动控制中应用很多，但缺少相对应的可以使控制器稳定的方法.文中将离散时间准无限时域模型预测控制理论运用到USV轨迹跟踪中，并证明了所设计的控制器的稳定性.通过仿真验证了所设计控制器收敛性较传统线性MPC控制器更强，跟踪过程中误差更小.

1 控制器设计

1.1 系统模型

USV属于多输入多输出系统，所以采用状态空间模型进行研究，选取Perez 等[9]提出的船舶状态空间模型作为USV的动力学模型.

只考虑船舶前进、横漂和艏摇三个自由度，驱动力只有纵向推力和转艏力矩，USV轨迹跟踪示意图见图1.

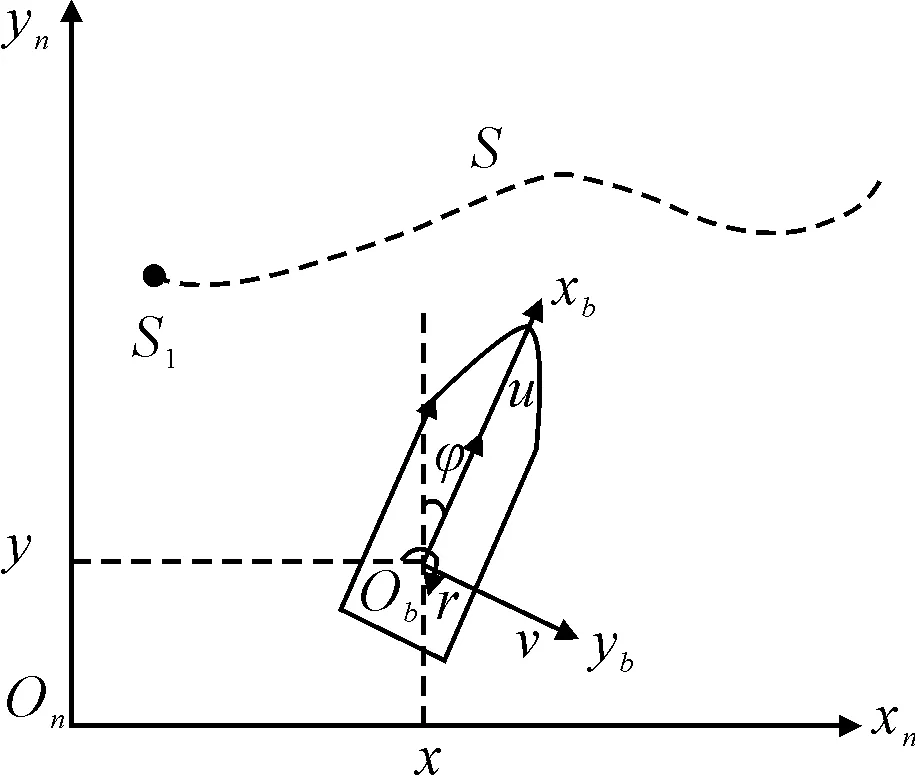
xnonyn-大地坐标系；xbobyb-USV的随体坐标系；s-目标轨迹；s1-轨迹的起始点

USV的水平面三自由度运动模型为

(1)

式中：x,y,φ为位置和姿态角信息；u,v,r为速度信息；τu为USV纵向推力；τr为USV转艏力矩，由于文中考虑的是欠驱动船舶，所以无侧向推力；m11,m22,m33为含附加质量系数在内的惯性系数；d11,d22,d33为阻尼系数.

1.2 模型的线性化及离散化

由于本文旨在追踪任意一条直接给点的轨迹，参考文献[10]中近似化方法，假设参考系统已经跟踪了给定的轨迹，得到了轨迹中每个时刻的状态量和控制量，通过对参考系统与当前实际系统的偏差处理，设计模型预测控制器以达到轨迹跟踪的目的.其中，参考系统的系统方程为

(2)

式中：χR=[xR,yR,φR,uR,vR,rR]T为参考系统的状态量；τR=[τuR,τrR]T为参考系统的输入控制量.

实际系统在任意点(χR,uR)进行泰勒展开，保留一阶项可得：

(3)

式中：χ为USV实际系统的状态量；τ为实际系统的输入控制量.结合式(2)～(3)可得：

(4)

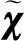
结合式(1)，可得A,B矩阵为

(5)

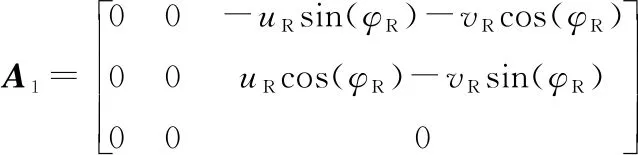
考虑到模型预测控制器需要离散式的模型，对式(5)采取欧拉法离散，可得：

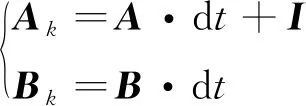
(7)

式中：dt为时间步长；I为单位矩阵；k为任意时刻.

1.3 设计目标函数

(8)

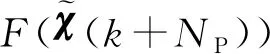
为使目标函数便于数值求解，以Δτ(k+i)为参量，设计：

(9)

结合式(7)，可得新的系统表达式：

(10)

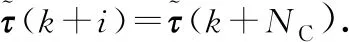
Ak+i=Ak,Bk+i=Bk,i=1,2,…,NP

(11)

参考文献[8]，求式(8)中的终端惩罚函数.

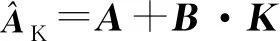
选取一个参数κ使其满足条件：

κ>1

(12)

求解离散形式的Lyapunov方程：

(13)

可得唯一确定的正定矩阵P，且存在α∈(0，∞)，使平衡点的某一邻域：

(14)

(15)

结合式(8)、式(15)，可将目标函数改写为

(16)

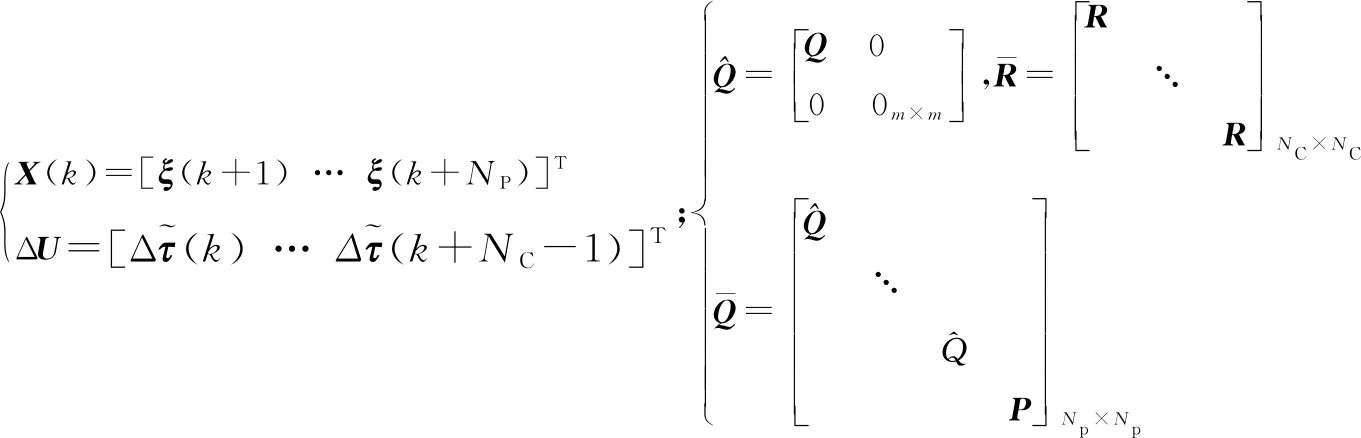
则系统的模型预测表达式可写为

X(k)=Ωξ(k)+ΓΔU

(17)

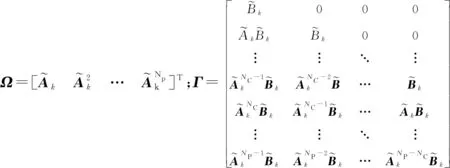
将式(17)代入式(16)并忽略掉与ΔU无关的项可得：

(18)

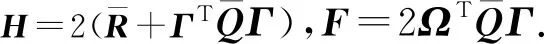
1.4 约束条件设置

USV在实际工况中受执行机构如螺旋桨、舵等机械结构的限制，映射到控制算法中就是需要对USV的输入力τu、力矩τr以及输入增量Δτu、Δτr进行限制.同时考虑到USV操纵性能，需要对其输出量进行约束，本文研究的是轨迹跟踪，需要同时考虑对6个状态量的要求，所以将6个状态量均看作输出量，进行约束限制，参考文献[5]，具体约束形式如下.

Δτmin≤Δτ(k+i)≤Δτmaxi=0,1,2,…,NC-1

(19)

τmin≤τ(k+i)≤τmaxi=0,1,2,…,NC-1

(20)

(21)

结合式(18)，可以把控制问题转化为下式的优化问题求解：

s.t. ΔUmin≤ΔU(k)≤ΔUmax

Umin≤C·ΔU(k)+U(k)≤ΔUmax

ζmin≤ζ(k)≤ζmax

(22)

式中：ΔUmin=INC⊗Δτmin,ΔUmax=INC⊗Δτmax

Umin=INC⊗τmin,Umax=INC⊗τmax

ζmin=INC⊗χmin,ζmax=INC⊗χmax

式中：INC为行数为NC的单位列向量；INu为维数为控制输入维度的单位矩阵；⊗为克罗内克积.

2 稳定性证明

参考文献[8]，分两步证明本文设计的控制器稳定性问题，首先证明终端惩罚函数可以替代无限预测时域.

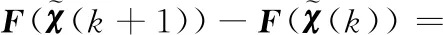
(23)

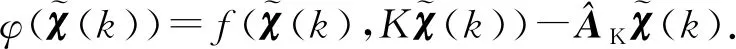
(24)

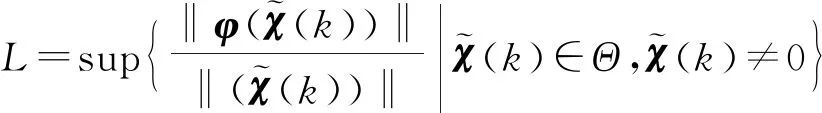
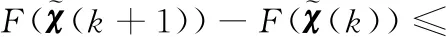
(25)

当κ>1且α→0时，下式成立

(26)

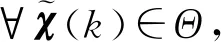
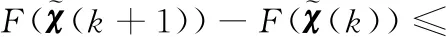
(27)

对式(27)从k→∞时刻进行求和，则有

(28)

(29)

第二步证明系统稳定性.

结合式(4)可得，(0,0)点为系统的平衡点，且(0,0)表示任意一处USV实际系统跟踪上参考轨迹点的工况，与USV实际系统根据模型预测控制的原理，结合式(8)，式(10)可以将k时刻目标函数的最小值即最优值记为

(30)

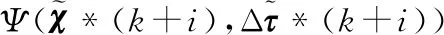
k+1时刻考虑可行解的目标函数值可写为

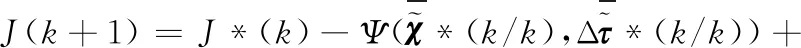
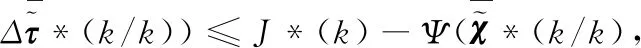
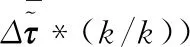
(31)

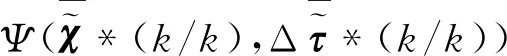
考虑到最优解应该小于可行解，则有：

J*(k+1)≤J(k+1)≤

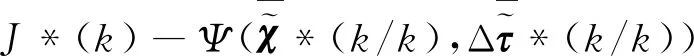
(32)

可证J*(k)是单调不增的，即系统在设计控制器作用下渐进稳定.

3 仿 真

3.1 仿真参数

为验证算法可行性，参考文献[11]中简化后的模型，模型参数见表1.

表1 USV模型参数

3.2 仿真工况与参数

为证明文中所设计算法的普适性和优越性，分别进行直线与正弦曲线轨迹的仿真实验，并与文献[5]中的算法进行比较.具体工况与参数如下.

工况1跟踪直线，跟踪参考轨迹为

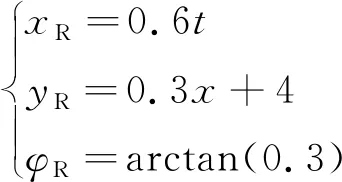
期望轨迹的速度量可以通过给定轨迹位置量微分得到，为

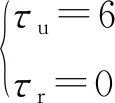
约束条件为

与文献[5]中的基于线性模型预测USV轨迹跟踪控制器进行结果比较，将优化问题式(22)进行仿真，得到的仿真结果见图2～4.

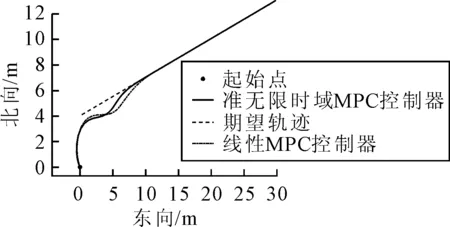
图2 跟踪轨迹比较

由图2可知:所设计控制器与线性模型预测控制器均可跟踪给定轨迹，但在初始位置与目标轨迹偏差较大的情况下，加入终端惩罚函数即本文设计的准无限时域模型预测控制器相对于线性模型预测控制器在跟踪直线轨迹时，误差幅值更小，且可以更快的收敛于给定轨迹.

由图4可知:所设计控制器输入力和力矩收敛于定值，由图3可知，USV状态量在此控制器输入下收敛于定值，符合所跟踪直线轨迹的期望状态量，验证了所设计控制器的稳定性.

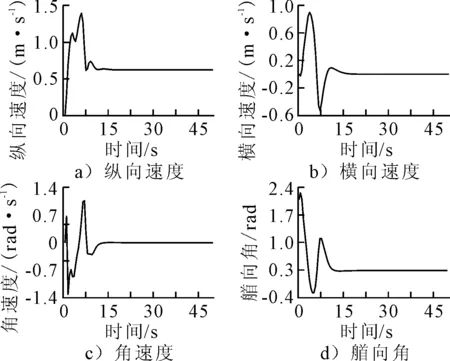
图3 USV状态量

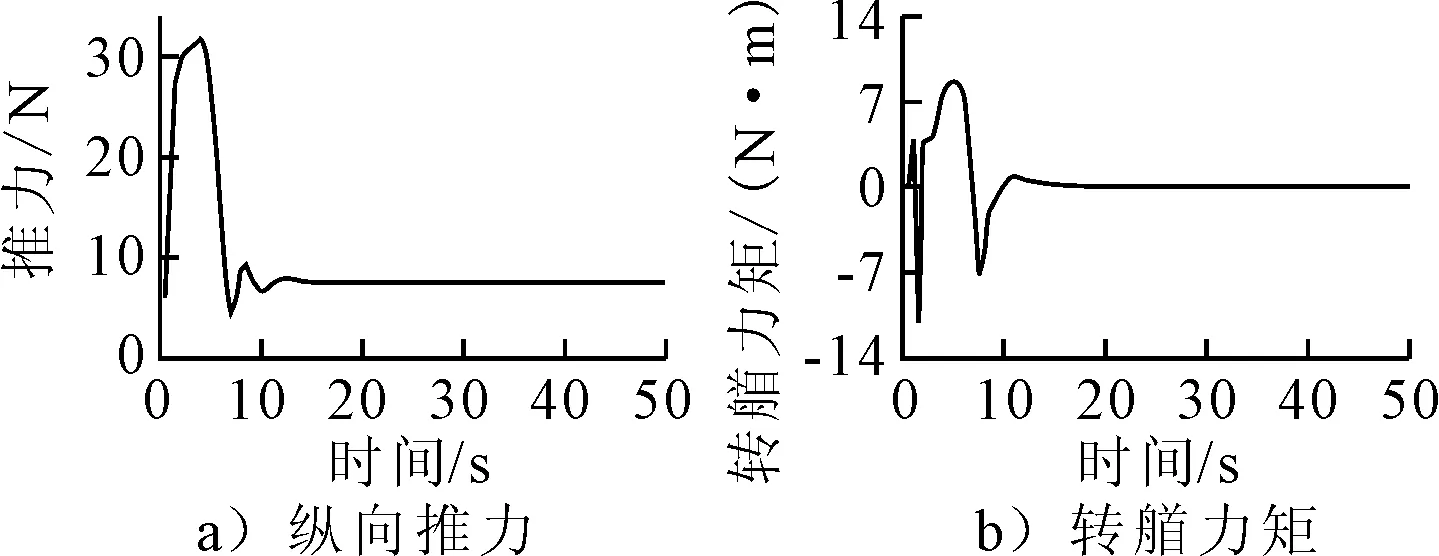
图4 USV控制量

工况2 跟踪正弦曲线,选取参考轨迹为

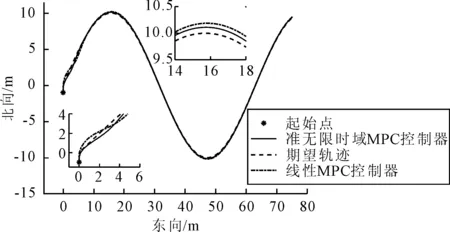
图5 跟踪轨迹比较

由图5可知:本文所设计控制器与线性模型预测控制器均能跟踪上期望轨迹，但在初始位置有偏差时，USV在本文所设计控制器控制作用下，可以更快地收敛于期望轨迹且误差幅值要比线性模型预测控制器要小.在正弦曲线轨迹曲率最大处，文中所设计控制器跟踪期望轨迹误差更小.

由图6可知，USV状态量在此输入下也呈现周期性变化，符合USV航行轨迹为正弦曲线时的状态量变化趋势.由图7可知，所设计控制器输入力和力矩呈周期性变化.

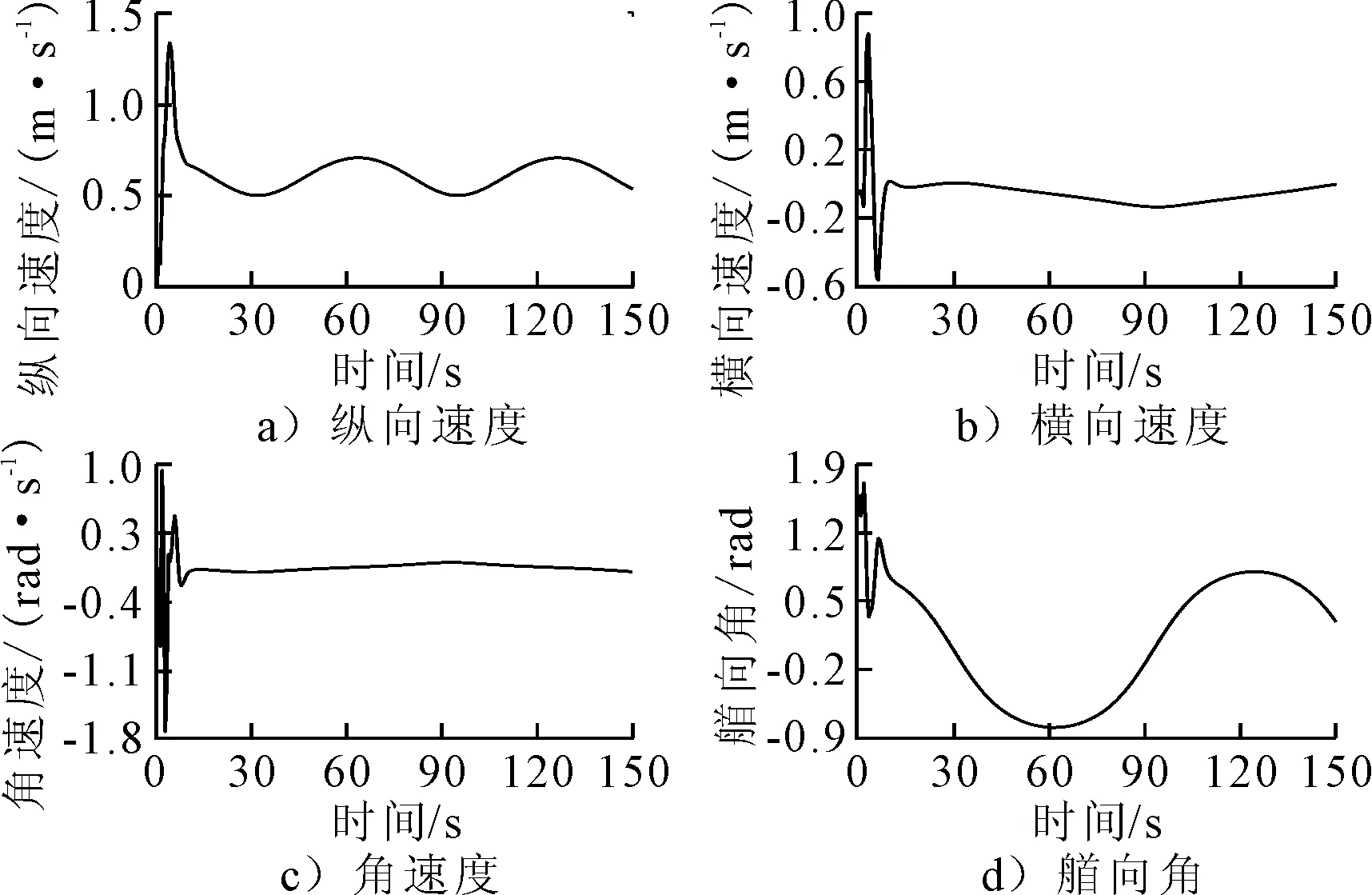
图6 USV状态量

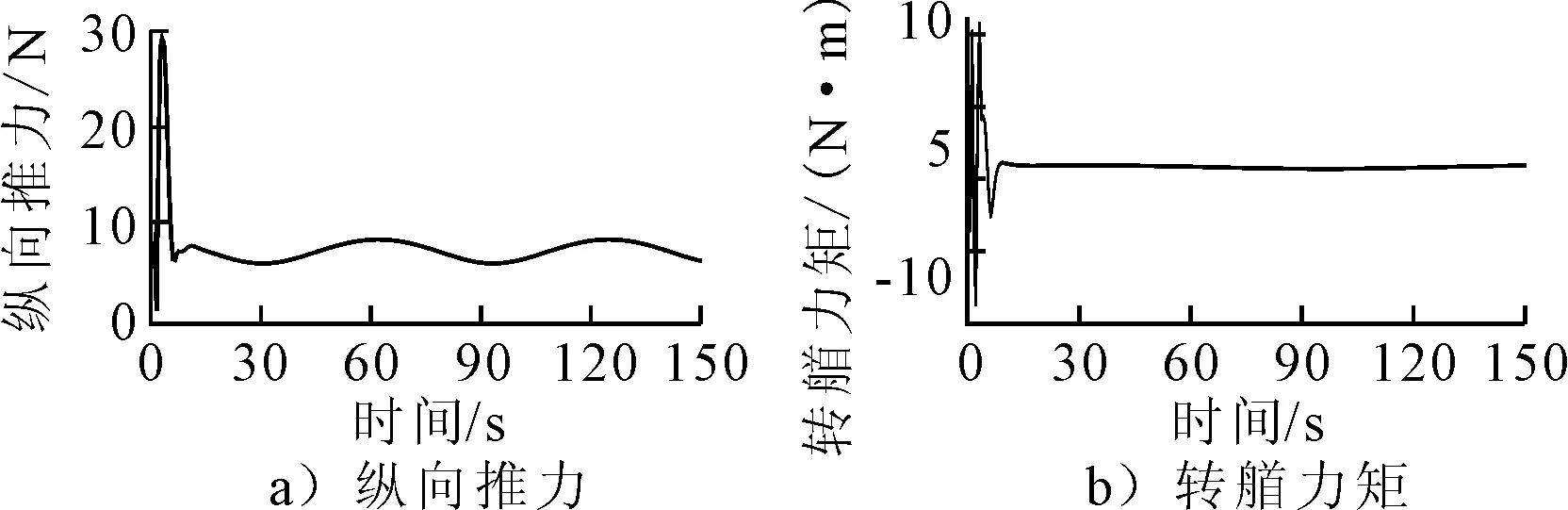
图7 USV控制量

4 结 论

1) 将准无限时域模型预测控制理论拓展到USV轨迹跟踪控制器设计中.设计了一种基于准无限时域的模型预测控制器，并证明了所设计的控制器是稳定的.

2) 通过在仿真平台上进行直线轨迹以及正弦曲线轨迹的仿真验证，证实了本文所设计控制器的稳定性和普适性.相较于线性模型预测控制器，本文所设计控制器可以更快的收敛到期望轨迹，且在跟踪轨迹过程中，与期望轨迹的误差更小.本文的不足之处在于未考虑扰动的影响，后续将作进一步研究.