城市干道分段绿波协调控制模型研究

2022-01-12徐文洁

武汉理工大学学报（交通科学与工程版） 2021年6期

酆磊赵欣* 李林张赛徐文洁

(武汉理工大学交通与物流工程学院1) 武汉 430063) (桂林电子科技大学建筑与交通工程学院2) 桂林 541004)(智能交通系统广西高校重点实验室3) 桂林 541004)

城市路网密度的不断增加会导致交叉口数量的急剧增加.城市交通需求的不断扩张，会直接导致城市整体交通服务水平的降低，排队拥堵现象也日益严重.因此，加强交叉口之间的相关性，对城市干道协调控制是必然的结果[1].

Little等[2-3]提出了绿波协调控制理论.经典绿波控制考虑的交通模型比较理想，但随着交叉口数量的增多其控制效果逐渐变差.随着协调控制范围的需求不断扩大，现有文献主要是对模型的改进和扩展[4-8]，虽提高了模型的适用性，但其控制范围并没有得到扩大.尤其是在现有城市干道，信号控制交叉口众多且跨度较长，路口特征及交通流量差异较大.现有绿波协调控制模型无法对城市长干道进行大范围协调控制.需要解决干道如何根据不同交通特征实现精准分区分段控制及相邻绿波段之间的协调控制.

1 多段绿波控制模型

1.1 绿波分段

随着现在道路路网密度不断增加，路段和交叉口差异性不断拉大.经典绿波协调控制方法显得效率低下，难以实现较为理想的控制效果.为提高绿波协调控制的控制效果，需将差异较大的路段和交叉口分段协调.

绿波分段首先要满足关联性的要求，为表征交叉口间的关联性，采用简易的耦合度模型，给出协调子区的合并阈值Rcom，为

(1)

(2)

通过比较绿波带宽最大通行能力与实际流量的大小找到绿波带宽的瓶颈点，对主干道绿波进行分段，为

(3)

Qsi,i+1=Qsm,i+Qsl,i+Qsr,i-Qsl,i+1-Qsr,i+1

(4)

式中：NVi,i+1为一个周期从路口i到路口i+1不停车通过的车辆数；BWi,i+1为路口i至路口i+1的绿波带宽；LNi,i+1为路口i或路口i+1在协调方向的直行方向的车道数；C为信号公共周期时长；ht为车辆通过路口的饱和车头时距；Qsi,i+1为协调方向上驶入路口i的直行车辆数；Qsm,i为路口i的直行车流量；Qsl,i为路口i的左转车流量；Qsr,i为路口i的右转车流量；Qsl,i+1为路口i+1的左转车流量；Qsr,i+1为路口i+1的右转车流量；通过比较NVi,i+1与Qsi,i+1的大小找到绿波瓶颈点，此处为饱和度较高的路段，对其进行分段.结合上述两个因素考虑，通过图1流程图进行主干道分区分段.

图1 绿波分段子区划分算法流程图

1.2 多段绿波控制模型

在经典绿波控制模型的基础上[9]，通过上述绿波分段方法将主干道分成若干段绿波，形成多段绿波，其控制模型为

(5)

s.t.

(6)

1/Csi,max≤z≤1/Csi,min

(7)

wsi,i+bsi≤1-rsi,i

(8)

(9)

(10)

(11)

(12)

2 相邻绿波段间的协调模型

绿波分段后需对相邻绿波进行协调，通过集合的运算方法，将单向拓展成双向绿波协调[10]，其具体模型如下.

2.1 相邻绿波段间的协调模型

图2 相邻绿波间协调模型示意图

由于上游子区公共周期与下游子区公共周期不同，考虑双向交通对车辆达到时间区间和绿灯时间区间的分析均以两个相邻子区周期时长的最小公倍数K为单位.在时间区间[0,K]内，上游子区周期循环次数为n，下游子区周期循环次数为m，假定在零时刻，上游子区最后一个路口与下游子区第一个路口的相对相位差为φ，那么可以做以下分析.

1) 车辆从i路口达到i+1路口的时间区间为

(13)

那么，在[0,K]内，从路口i到路口i+1的到达时间区间的集合为

X=x1,x2,x3,…,xn

(14)

2) 路口i+1的绿灯时间区间

(15)

则在[0,K]内，路口i+1的绿灯时间区间集合为

Y=y1,y2,y3,…,ym

(16)

3) 同理，可以得到反向车辆从路口i+1到路口i的时间区间和路口i的绿灯时间区间，为

(17)

则在[0,K]内，车辆从路口i+1到路口i的时间区间集合为

(18)

路口i的绿灯时间区间：

(19)

则在[0,K]内，路口i的绿灯时间区间集合为

(20)

要得到两相邻子区最佳协调相位差φbest，通过求解最优φ将上、下游绿波带连接起来形成整体协调系统.φ的求解为一个线性规划问题：max{(X∩Y)∪(X′∩Y′)}：

maxz(φbest)={(X∩Y)∪(X′∩Y′)}

(21)

(22)

2.2 分段绿波协调模型控制结构

分段绿波协调控制模型可分为子区内部协调控制与子区外部协调控制，子区内部即同一个子区内采用最大绿波带宽协调控制，而子区外部采用1.2所阐述的连接算法控制，可将无协调的绿波带间接连接协调.其控制结构可分为三级:一级控制单位指需要协同控制的城市干道；二级控制单位指各协调子区，即单段绿波；三级控制单位指节点交叉口，每个实际控制的单点信号控制路口.

3 试验设计及仿真

3.1 仿真设计

仿真以桂林市中山路北段为案例，南至芦笛路口北至芳华路口，共七个信号控制交叉口，具体仿真模型见图3.

图3 仿真模型

通过实际调查得到交通流量数据和信号控制数据后，利用Synchro进行节点信号配时统一周期时长.再利用Lingo得出绿波协调控制对应相位差及绿波带宽，最后通过VISSIM对不同控制方案下进行仿真试验.方案一采用经典绿波协调控制，方案二采用分段绿波协调控制.仿真时长共计1 200 s，剔除仿真初期车流不稳定数据，得出最终仿真结果.

根据实际调查数据，通过Synchro、Lingo等软件的计算，可得到经典绿波控制与分段绿波控制的信号控制基本参数见表1～2.

表1 经典绿波协调控制参数

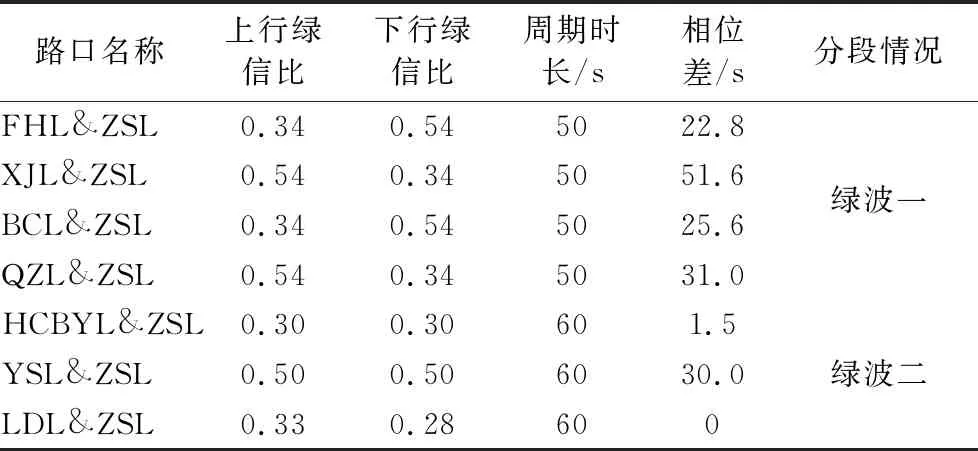
表2 分段绿波协调控制参数

3.2 仿真结果分析

通过仿真输出结果汇总分析可得实施经典绿波控制和分段绿波控制下的各路口延误时间、停车次数以及排队情况见图4.各评价指标节点优化效果见表3.

表3 各评价指标节点优化效果单位：%

图4 优化前后各路口延误时间、停车次数以及排队情况

仿真试验中，把芳华路口至群众路口分为第一段绿波，环城北一路口至芦笛路口分为第二段绿波.从仿真的试验数据可以看出：芳华路口至群众路口各项指标相似，环城北一路口至芦笛路口也比较接近，这也验证了上述绿波分段的原理.从仿真效果来看，除虞山路口外，其余路口均有不同程度的优化效果.虞山路口处在环城北一路口与芦笛路口之间，这两个路口均为饱和度比较高的路口，绿波分段时将其划分到了一个绿波段子区.由于上、下游相邻的两个路口均为流量比较大的路口，所处子区的公共周期变大，导致虞山路口产生不必要的停车延误时间.因此在优化整体路段时，可能会引起个别路口延误增加，这也是模型下一步需要优化改进之处.

协调控制系统的优化需遵循整体最优原则，根据仿真输出结果，其整体评价结果见表4.