协同自适应巡航控制车辆跟驰模型优化及仿真分析

宋成举

(东北林业大学交通学院 哈尔滨 150040)

0 引 言

跟驰理论是智能车辆系统的技术基础，也是智能车路合作的关键技术，在实际的交通流运行过程中，驾驶员需要结合具体交通环境而做出不同的驾驶决策，受制于个体的辨别能力的差异，车辆的跟驰行为表现存在较大差别，往往容易导致交通流的不稳定状态，产生交通紊流，进而可能诱发各种交通问题.

经过多年的理论研究，针对不同的跟驰行为已经建立起多种跟驰模型.陈斌等[1]针对三种跟驰模型的稳定性、真实性开展数值模拟分析，引入主观意愿、驾驶环境等不确定因素，提出了具有良好综合性能的跟驰模型.王殿海等[2]将跟驰模型划分为统计物理角度和交通工程角度，明确了各种跟驰模型的归属于特征，阐释典型模型的建模思路及发展趋势.Tang等[3]考虑了驾驶员的预判，建立了融合驾驶员预测的跟驰模型，并证实了该模型具有良好的时间稳定性.邱小平等[4]依据经典Gipps安全距离规则对NaSch模型改进，提出了基于安全距离的自动驾驶元胞自动机交通流模型，可以明显提高道路通行能力，且混合交通流条件下可以缓解拥堵.张立东等[5]采用状态空间法和控制系统的稳定性判据对全速度差最优模型进行了稳定性分析，得到了弯道情况下的交通流稳定条件.何兆成等[6]通过引入横向分离参数，建立了考虑横向分离与超车期望的车辆跟驰模型.秦严严等[7-8]建立了基于非线性动态车头间距策略的协同自适应巡航控制(CACC)跟驰模型，推导不同CACC比例下的混合交通流基本图模型，给出混合交通流稳定性判别条件，计算混合交通流稳定域，分析混合交通流稳定条件下临界比例与车头时距的解析关系，提出可变车头时距设计策略.Vicente等[9]在量产车辆上实现了智能驾驶模型的应用，在不同交通情况下对控制器进行了响应测试.章军辉等[10]针对高速公路车队稳定性问题，根据Lyapunov稳定性理论，采用加权二次型性能泛函以及线性矩阵不等式约束，将协同式多目标自适应巡航设计转化成带约束的在线凸二次规划问题，并实现了仿真分析.

上述研究都在不同角度对跟驰理论的完善与技术应用起到了积极作用.但相关文献并未给出前车行驶状态动态变化的条件下，后车的响应状态.鉴于此，文中考虑前后车辆动态跟驰状态下的跟驰行为，改进CACC模型，对比模型跟驰效果，并进一步分析不同参数变化对于跟驰队列的影响，获取跟驰队列的时变规律.

1 模型构建与数值仿真

1.1 模型简介

跟驰模型是驾驶环境对驾驶行为影响的数学描述.经典跟驰模型起源于驾驶动力学，采用车辆加速度反映跟驰决策，而跟驰决策的制定则取决于前车运行决策、前后车辆的速度差和空间位置关系，还与自身的运行状态有关.经典跟驰模型的一般公式为

(1)

式中：an+1(t+T)为t+T时刻n+1车的加速度；vn+1(t+T)为t+T时刻n+1车的速度；Δv(t)为t时刻前后相邻车的速度差；Δx(t)为t时刻前后相邻车的距离；α，m，d均为待标定常数.

美国加州伯克利大学在总结前期关于CACC模型研究成果的基础上，提出了恒定车间距的CACC跟驰模型，模型认为跟驰车辆的加速度取决于三部分：前车的加速度、前后车辆的速度差和实际车头间距与期望车头间距之间的误差项，其中，恒定车间距被视为影响车头间距误差项的关键因素，其模型结构为

(2)

Bart等[11]给出待定系数的建议值：α=1.0，β=0.2，γ=3.0.该模型具有结构简单、含义清晰具体的特点，是基于恒定车时距的最为常用的跟驰模型.

1.2 模型改进

跟驰车辆之间车头间距与前后车辆的速度之间存在一定的相关性，即在不同速度条件下，期望间距存在一定差异.

1) 在自由流状态下，期望车头间距往往不存在约束，数值表现为极大值.

2) 在交通拥堵状态下，期望车头间距近似为车身长度与安全距离之和，数值表现为L+S0.

3) 在正常交通状态下，期望车头间距应为车速的增函数.

基于以上特性，期望车头间距Hd(t)为

Hd(t)=(L+S0)/(1-(v(t)/v0)k)

(3)

设y(t)=v(t)/v0，z(t)=(L+S0)/Hd(t)，公式(3)变为

z(t)=1-y(t)k

(4)

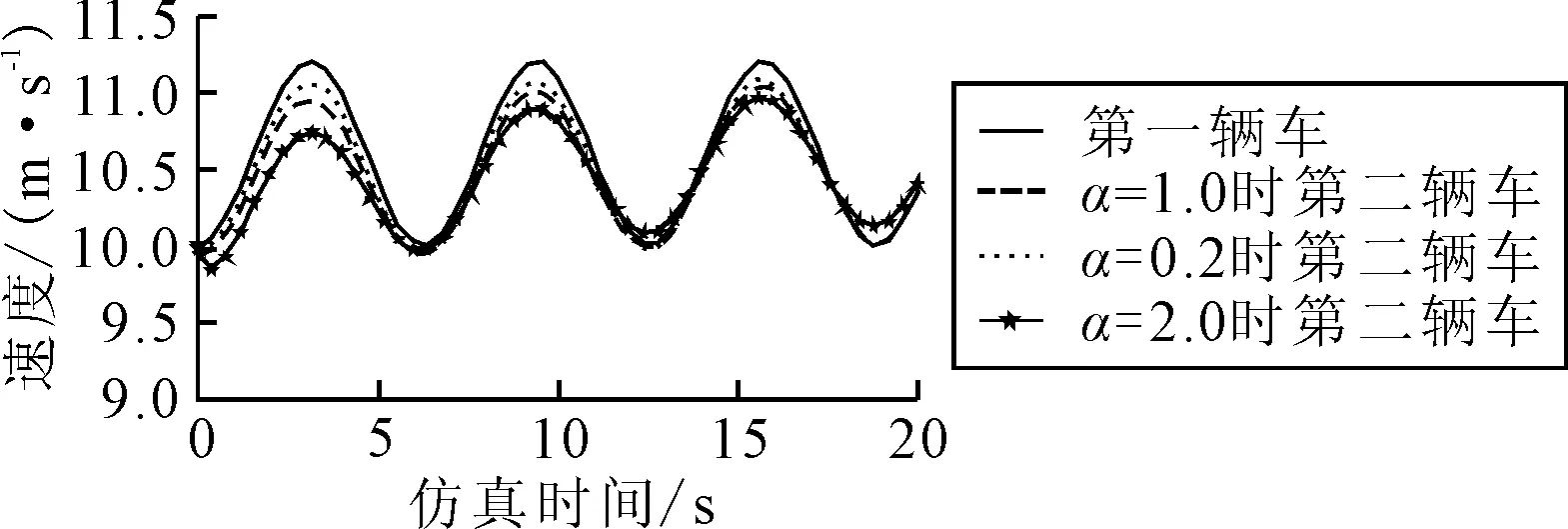
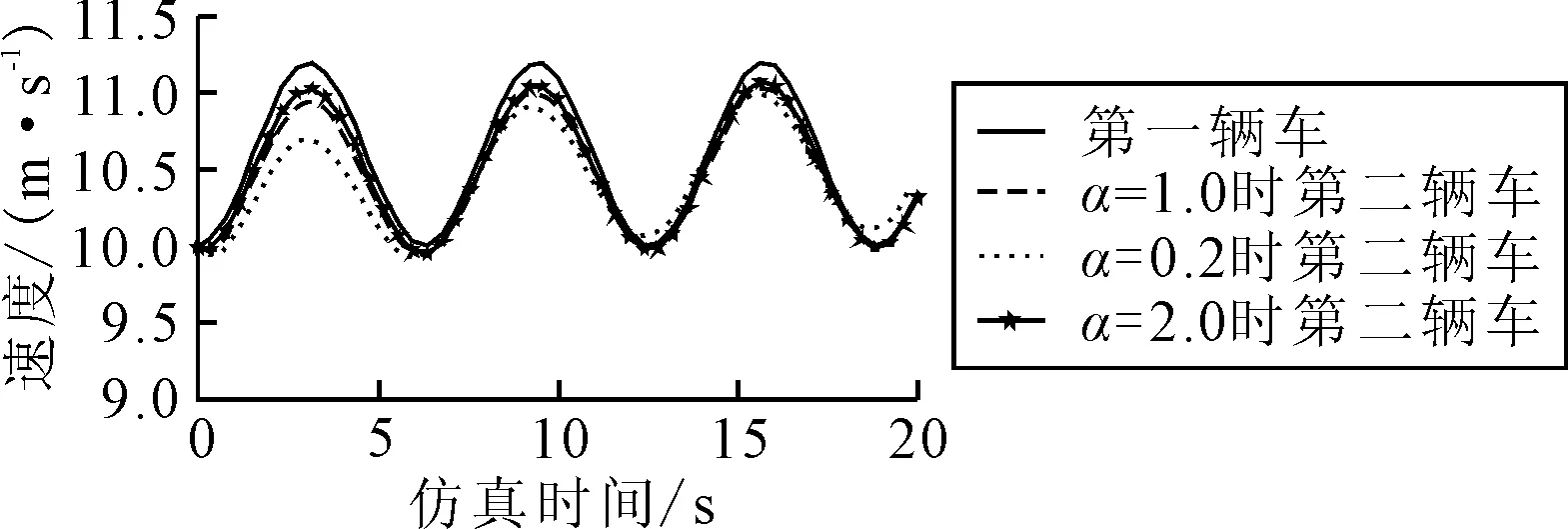
由参数定义可知，0

1) 为了保证函数有效，可知k≠0.

2) 当k<0时，由于v(t)

3) 当k>0时，Hd(t)与k值正相关，分别取01，式(4)呈不同的增长态势，对比见图1.

图1 不同k值条件下z值变化

改进的模型充分保留了原CACC模型的基本结构，并反映了不同车速条件下，车头间距的动态变化特征，将式(3)代入式(2)可得：

(5)

1.3 数值仿真环境构建

该队列由5辆标准车组成，以某一初始速度v0匀速运动，假定在时刻t，该队列首车受到干扰，首车在干扰下要做出加速或减速的行驶决策，为便于仿真分析，本文将车辆加、减速决策变化规律视为正弦波动，后续车辆的运行状态由前车及跟驰函数决定，前车加、减速变化的函数形式为

v=Asin(ωt)

(6)

式中：A为首车加速度的幅值，m/s2；ω为首车加速度的角频率，rad/s.

取跟驰队列车辆v0=10 m/s，L=20 m，S0=5 m.考虑到行驶舒适性，加、减速度最大值取0.6 m/s2，即首车加速度振幅A=0.6 m/s2，角频率取ω=1.0 rad/s.

2 模型对比分析

2.1 原CACC模型中跟驰队列速度变化

参考Bart van Arem推荐的跟驰模型参数，将其输入到仿真环境下的跟驰队列，为了简化仿真过程，假定式(5)中k=1.设定跟驰队列环境，扰动条件同前，队列中各车辆速度变化见图2.

图2 原CACC模型跟驰队列车速变化

由图2可知：队列车辆均与首辆车速度变化趋势相同，但速度波动幅度逐渐减小，这符合交通波的传导规律，也说明后车的运行状态受到前车制约，随着跟驰时间的延长，队列中的车辆速度有趋近统一的倾向，保持稳定的车辆间距行进.

2.2 改进CACC模型中跟驰队列速度变化

同样设置改进CACC模型的队列环境，扰动条件同前，队列中各车辆速度变化见图3.

图3 改进CACC模型跟驰队列车速变化

由图3可知，队列车辆速度变化趋势相同，速度差最大值出现在第一个波峰，后续波峰的速度差值逐渐缩小，队列车辆速度的波动幅度逐渐降低，直至速度统一，维持队列稳定.

2.3 改进前后队列速度变化对比

为了对比两个模型的跟驰效果，本文仅对比两个队列的第二辆车的跟驰效果，见图4.

图4 不同模型条件下跟驰队列速度变化曲线

由图4可知：原CACC模型和改进后的CACC模型的车速状态均与第一辆车的速度保持同步变化，且随着车队的行进，跟驰车辆与队列第一辆的速度差呈缩小趋势，这与车队跟驰间距初始值偏大有关，随着仿真时间延长，跟驰队列的跟驰间距逐渐趋于稳定状态，但在相同观测时间节点，改进后的CACC模型与队列第一辆车的速度差更小，当仿真时间延长时，改进后的CACC队列的间距可以很快趋于稳定，且间距更小.

通过仿真对比，可以看出改进的CACC模型可以更好的引导跟驰队列的跟驰行为，缩小跟驰车辆之间的车头间距，相同条件下，跟驰控制更精细.

3 改进CACC跟驰模型特性分析

3.1 不同值条件下跟驰特性

参考前文中改进CACC模型，原模型中假定k=1，保持其他参数不变，分别输入k=1，0.5，2，观察跟驰队列第二辆车的速度变化情况，见图5.

图5 不同k值条件下模型跟驰特性对比

由图5可知：k值的大小并不影响跟驰队列中车速的变化趋势，均与前车速度变化趋势相同，当k值小于1时，跟驰车辆的速度值明显小于前车，表明跟驰车辆有进一步扩大车头间距的趋势；而当k值大于1时，跟驰车辆的速度值比前车速度大，表明跟驰车辆有进一步缩小车头间距的趋势.为了进一步说明不同k值对车头间距的影响，延长仿真时间至100s，观察不同k值条件下车头间距的变化情况，见图6.

图6 不同k值条件下车头间距对比

由图6可知:车头间距均从初始值快速达到稳定态，k值影响跟驰队列稳定态大小，k值越大，跟驰队列稳定态车头间距越小，但k值并不影响达到稳定态的时间，扰动幅值与频率的变化对稳定态及达到稳定态的过程影响微弱.

3.2 不同α值条件下跟驰特性分析

参考前文中改进CACC模型，原模型中α=1，保持其他参数不变，分别输入α=1.0，0.2，2.0，不同α值条件下跟驰特性和车头间距对比见图7.

图7 不同α值条件下跟驰特性和车头间距对比

由图7a)可知：当α<1.0时，跟驰车辆状态变化不大，速度的波动幅度略有降低，跟驰队列运行状态表现较为稳定，具有一定的自我修复能力；当α>1.0时，由于初始条件并不是跟驰最优状态，跟驰车辆速度的波动幅度均呈增加的趋势，但后车跟驰行为受到前后车辆速度差的反馈控制，跟驰车辆速度很快又调节到前车速度值以下，随着波动时间的增加，前后车辆间速度差值趋于稳定，表明跟驰模型具有较强的纠错能力，其对应的车头间距变化见图7b).

由图7b)可知：车头间距总体呈波动式递增趋势，不同取值条件下，车头间距存在一定范围的交错，交错范围呈增大趋势，直至达到稳定态，此外，波动周期、达到稳定态的时间均与α值无关；随着α值越大，前后车辆车头间距的波动范围越小.

3.3 不同β值条件下跟驰特性分析

参考前文中改进CACC模型，原模型中β=0.2，保持其他参数不变，分别输入β=0.2，0.1，0.5，观察跟驰队列第二辆车的速度变化情况，见图8.

图8 不同值条件下模型跟驰特性对比

由图8可知：β值并不影响跟驰队列的车速响应趋势，但随着β值的增大，队列中跟驰车辆的速度波动幅度变小，说明车头间距呈现往复变化，当第一辆车在加速状态时，队列之间的车头间距逐渐扩大，当第一辆车车速下降到与后车车速相同时，车头间距达到最大值，而后逐渐降低，且车头间距最大值逐渐变小，直到达到车头间距最小值，之后往复直至在某一范围内波动.

3.4 不同γ值条件下跟驰特性分析

参考前文中改进CACC模型，原模型中γ=3.0，保持其他参数不变，分别输入γ=3.0， 1.0，5.0，观察跟驰队列第二辆车的速度变化情况，见图9.

图9 不同值条件下模型跟驰特性对比

由图9可知：随着γ值的增加，达到稳定状态时跟驰车辆的与前车的速度差越小，速度的波动频率保持不变，γ值越大，跟驰车辆与前车达到稳定跟驰状态的时间越短，且稳定跟驰状态时车头间距越小.

4 结 论

1) 考虑跟驰车辆期望间距与当前车速之间存在相关性，对经典CACC跟驰模型中的期望间距进行改进，构建了动态期望间距条件下的CACC跟驰模型，该模型能够更好的维持跟驰效率，符合不同交通流条件下的跟驰特征.

2) 改进的CACC模型中，拟定前车扰动条件，观测不同参数条件下的跟驰效果，当k<1时，跟驰车辆逐渐拉大与前车间距；当k>1时，跟驰车辆有主动缩小与前车间距的趋势，直至稳定态；α取值影响跟驰车辆速度的幅值，但并不影响波动频率，α值越大，跟驰队列车头间距波动范围越大，并最终达到稳定态；β值影响车头间距稳态的波动范围，β值越大，其车头间距的波动范围越宽；γ值越大，跟驰队列达到稳定跟驰状态的时间越短，且稳定跟驰状态时车头间距越小.