一种宏微观结合的主干路交通流状态分类方法

张小丽 郭志勇 李红伟 周云月

(河海大学土木与交通学院1) 南京 210098) (武汉理工大学交通与物流工程学院2) 武汉 430070)(诸暨市交通运输局3) 绍兴 311800)

0 引 言

交通流状态的准确识别是实施车路协同、检测交通事件和快速路交通联合控制[1]等智能交通管理手段的基础.目前，交通状态分类方法主要包括基于微观交通流理论的车头时距法、基于宏观统计理论的聚类方法以及基于宏观交通流理论的相位法三种.

基于微观交通流理论的车头时距法通常利用车头时距将交通流分为自由流和跟驰状态两种[2-3].王福建等[4]将跟驰行为进一步分为强跟驰和弱跟驰，并证明了强跟驰和弱跟驰状态的存在，但同时也指出强弱跟驰状态的临界值很难给出.基于微观交通流理论的方法侧重个体车辆之间而非交通流整体的物理意义.

基于宏观统计理论的聚类方法是基于交通流宏观参数通过k-means、Fuzzy等聚类方法进行状态划分[5-6].通常按照道路服务水平标准或者聚类效果评价指标确定聚类的数量，一般为3～6个.该类方法注重交通流整体的拟合效果，但不能解释交通流的物理意义.

基于宏观交通流理论的相位法主要是三相流法[7-8]，并在此基础上进一步划分，达到4阶段[9]或者6状态[10].总体而言，相位法主要对非自由流进行分类，且很难获得交通状态的阈值，适用于高速公路匝道这些连续流交通设施，可得到交通流整体的物理意义，但忽略了个体车辆间的影响且无法给出各状态的确切阈值，不能满足交通管理实践中对交通流状态进行判断和评价的需求.

有学者结合宏观交通流理论和统计理论建立新的交通状态分类方法.如，Silgu等[11]结合两相法和k-means法设计了一种动态交通流状态分类方法.Celikoglu等[12]则采用了多变量聚类方法对动态交通流模态进行分类.此类方法基于传统两相流法，使用仿真数据划分交通流状态，其划分结果的有效性和可应用性值得商榷.

由此可知，现有交通状态划分方法仅考虑宏观参数或微观参数，而且多用于高速公路、快速路等非阻断交通流，针对城市道路阻断交通流状态分类的研究则相对较少.与高速公路连续交通流运行状态不同，城市道路受信号控制的影响，绿灯放行时，红灯期间排队等待的车流以车群形式通过路段，而后续到达的车辆大概率无需排队直接通过.文中提出一种适用于城市阻断交通流的状态分类方法.该方法基于实测数据，既考虑微观交通流中车辆之间的相互作用，也考虑宏观交通流中车流的总体特征，同时保证交通流整体的拟合性.与此同时，比较本文方法以及已有常用方法在城市主干路交通流划分的效果，验证本文所提方法的有效性.

1 数据采集与预处理

1.1 数据采集

选择南京市北京西路和中山北路作为调查道路，调查路段具体属性如表1所示.根据李笑语等[13]的研究，南京主干道上工作日早上交通流量由低峰转为高峰的时段为06:50-08:10时段.因此，选择晴朗天气的工作日上午06:50-08:10作为调查时间段，并采用录像法进行数据采集.

表1 调查路段属性

北京西路为不可跨线路段，摄像机1、2、3分别放置在距上游交叉口出口道约75 m(断面1)、路段中点(断面2)、距下游交叉口入口道约75 m处(断面3).中山北路为可跨线路段，摄像机1、2、3分别放置在距上游交叉口出口道约75 m(断面1)、路段可跨线处(距出口道约135 m)(断面2)、距下游交叉口入口道约100 m处(断面3).

将车型划分为小型车、中型车和大型车三类.北京西路共采集6 720辆车，小型车占96.63%，中型车占0.77%，大型车占2.60%，平均小时交通流量为1 500 veh/h，高峰小时交通流量为1 600 veh/h；中山北路共采集3 600辆车，其中小、中、大型车分别占79.42%、1.13%、19.45%，平均小时交通流量和高峰小时交通量分别为800，840 veh/h.北京西路车速范围为[2.44,53.00 km/h]，平均车速为18.93 km/h.中山北路车速范围为[2.64,64.51 km/h]，平均车速为19.61 km/h.两条路段虽然限速值不同，但实际车速接近.

1.2 数据预处理

1) 车头时距 仅考虑频率较高的车头时距区间.通过统计发现，北京西路车头时距大于15 s和大于25 s的频率百分比分别为10.70%和1.64%；中山北路车头时距大于15 s和大于25 s的频率百分比分别为13.20%和3.24%.因此，本文选取(0,25]s作为车头时距频率分布区间.

2) 车速 北京西路和中山北路超速车辆分别占总流量的0.65%和0.78%.违章行为不在本文的研究范围内，因此剔除超速车辆的交通数据.

3) 超车换道 北京西路和中山北路超车换道车辆数占车辆总数的0.061%和0.076%，可知，超车换道行为在两条道路发生频率较少.因此，调查路段适合用微观交通流理论对其交通状态进行分类.

1.3 统计间隔确定

稳定性是交通流特征分析的必要条件.标准差是衡量交通流稳定性的常用指标，并受统计间隔的影响.文献[14]建议公路交通流统计间隔是5 min，Jian等[15]选取1 min作为高速公路交通流数据的统计间隔.本文比较各统计间隔下的交通参数标准差以确定最佳的统计间隔.如图1所示，北京西路和中山北路在各统计间隔内流量的标准差均大于6 veh/period，速度标准差在1～3 min统计间隔内大于5 km/h，在4 min以后逐渐趋于稳定且小于5 km/h，当速度标准差在5 min时达到最小.选择5 min作为统计间隔.图1也可以看出，速度比流量稳定，更适合作为交通流状态分析的参数.

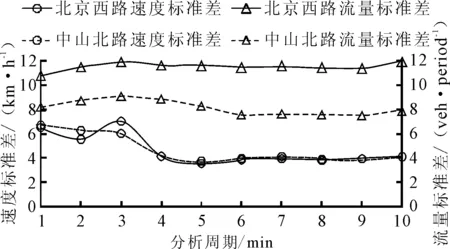
图1 统计间隔与交通参数标准差的关系

2 方法和应用结果

2.1 参数的选取

1) 宏观参数的选取 交通流量、速度和密度是交通流状态划分的常用宏观参数.在实际应用中，某一流量可能对应两个交通状态(如自由流和拥堵流)，不足以准确地反应交通流状态.Wang等[16]对高速公路实际数据研究发现交通拥堵并不是随着密度的增加而成比例的增加，密度不能准确反映交通流拥堵状态.对于速度，研究证明对拥堵交通流的分类效果很好[17].本文选择调查断面间的平均速度作为交通流状态分类的宏观参数.

2) 微观参数的选取 车头时距是最常见的微观参数，它既反映车辆之间相互跟驰情况，又反映交通流的随机性以及驾驶员反应时间等宏观交通参数无法反映的交通信息.Li等[18]研究表明，流量-密度图上的曲线形状依赖车辆的车头时距.Krbálek等[19]研究得出当交通流拥堵时，车头时距与速度相关.因此，本文将车头时距作为交通状态分类的微观参数.

2.2 方法设计

使用宏观交通参数和微观交通参数划分交通流状态的具体步骤如下.

步骤1利用k-means方法对速度进行聚类，得到初始交通流状态.

交通流通常被划分为2～6个状态.本文基于5 min的车速数据，利用k-means聚类法将交通流划分2～6个状态，并根据CH(Calinski-Harabasz)值选择最优的聚类数量，CH值越大，聚类效果越好.选取CH最大值对应的簇数作为最优的交通状态聚类数量，并得到各交通状态的速度阈值.

步骤2基于车头时距法对各状态交通流进行自由流和跟驰状态划分.

对k-means聚类出的每个状态使用相对速度绝对值法进行自由流和跟驰状态的划分.过程如下.

1) 在步骤1基础上进一步计算各个交通状态内的车头时距和相对速度.假设在调查路段中车辆匀速行驶，车头时距为断面2测得的数据.相对速度为

(1)

式中：Δv为相对速度，m/s；v前车和v后车分别为前车和后车的速度，km/h；Δt前车为前车通过断面1和断面3的时间差；Δt后车为后车通过断面1和断面3的时间差；X为断面1与断面3的距离.

2) 在各交通状态内，绘制车辆的车头时距与相对速度绝对值的曲线，从而建立车头时距与宏观速度之间的关系.曲线横坐标为车头时距，纵坐标为各车头时距下的相对速度绝对值的平均值.

3) 在各交通状态中，寻找车头时距与相对速度变化曲线里由倾斜转化为水平的转折点.曲线倾斜表示交通流处于跟驰状态，曲线水平说明交通流处于自由流，转折点则为自由流和跟驰状态的分界点.

步骤3利用坐标转换法得到明确的车头时距阈值.

相对速度法可以将交通流划分为自由流状态与跟驰状态，但不能得到确切的阈值.利用坐标变换法得到确切阈值，转换过程见图2.

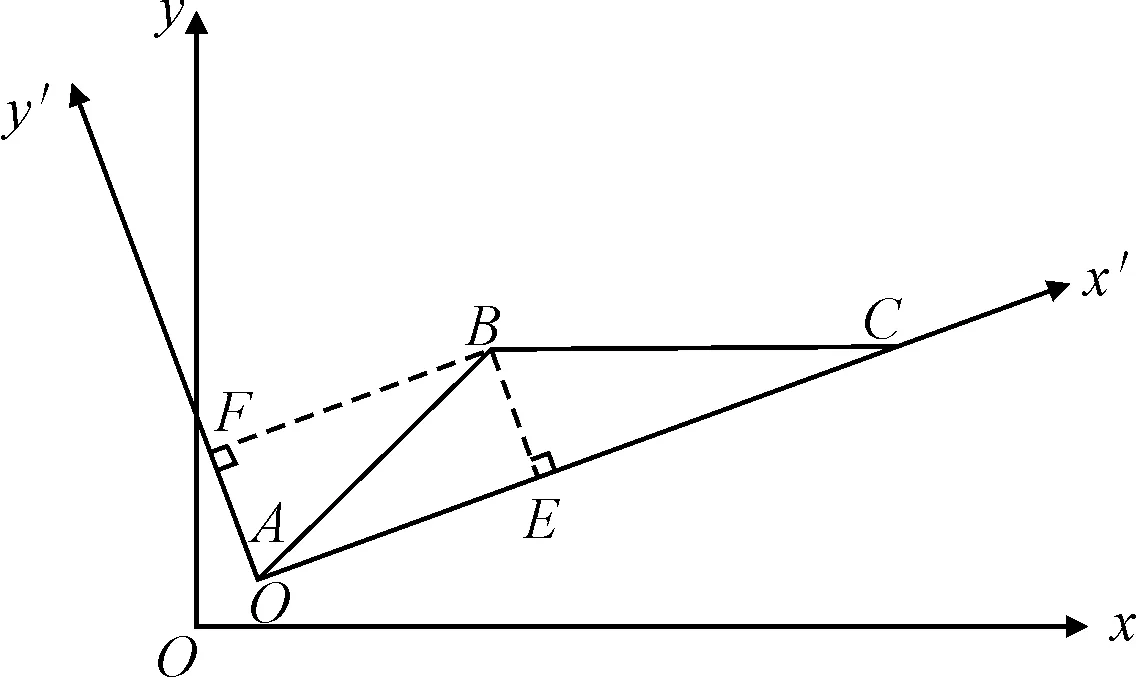
图2 坐标变换法确定自由流与跟驰状态阈值的过程

1) 建立坐标系 以车头时距为x轴，相对速度绝对值为y轴，建立车头时距与相对速度绝对值曲线坐标系.标出点A、C，点A和点C分别为车头时距为1 s和25 s时的相对速度绝对值.

2) 建立新坐标系 点A为新坐标系的原点，直线AC的延长线x’是新坐标系的x轴，作直线AC的垂直线y’，y’为新坐标系的y轴.

3) 计算曲线各点在新坐标下的坐标值 在车头时距与相对速度曲线上任取一点，以点B为例.画点B到新坐标系x轴和y轴的垂线，垂足分别为点E和点F，直线BE和BF的长度分别为B点在新坐标系中的y值和x值.

4) 确定车辆自由流与跟驰状态的阈值 新坐标系中y值最大的点就是曲线ABC的转折点，旧坐标系与之对应的x值，即自由流与跟驰状态的车头时距阈值.

2.3 案例应用

利用k-means聚类方法对速度进行聚类.CH值与交通状态种类数量曲线见图3.当聚类数量K为3时，两条道路上的CH均为最大值.因此，交通流分为三种状态：畅通、缓慢和拥堵，具体阈值见表2.

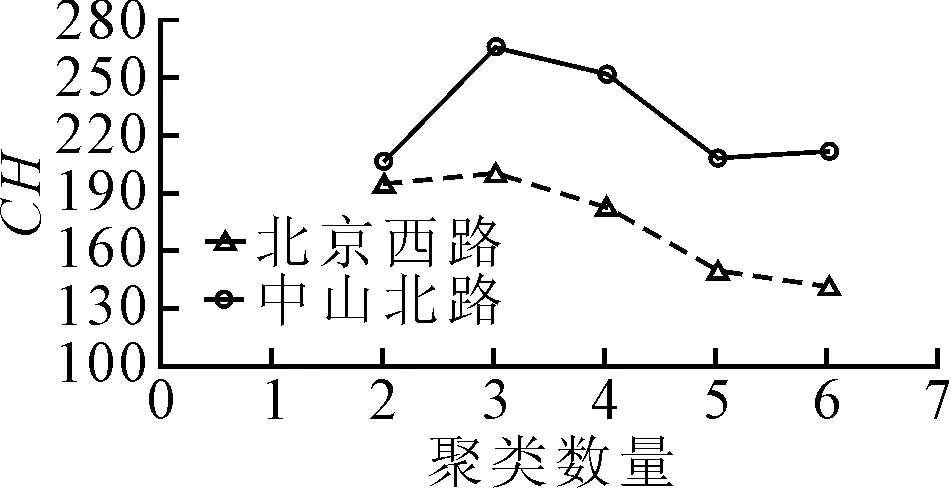
图3 CH与聚类数量关系

表2 基于k-means的交通状态划分结果 单位：km/h

在畅通、缓慢和拥堵三种交通流状态下绘制的车头时距与相对速度绝对值曲线见图4.有图4可知：①缓慢状态下，车头时距与相对速度曲线的关系发生变化.随着车头时距的增加，相对速度先线性增加，随后在某一数值范围内水平波动.缓慢状态存在自由流和跟驰两种交通状态.②畅通状态和拥堵状态下，车头时距与相对速度关系未发生改变.畅通状态下，随着车头时距的增加相对速度变化不大，交通流为自由流；拥堵状态下，相对速度与车头时距线性正相关，交通流为跟驰状态.

图4 不同交通流状态下车头时距与相对速度绝对值关系

对处于缓慢交通状态下的样本进行坐标转换，结果见表3.由表3可知：不可跨线路段跟驰临界值均为5 s，可跨线路段跟驰临界值均为8 s.当车头时距大于跟驰临界值时，为自由流状态；车头时距小于跟驰临界值时，为跟驰状态.在同区域同时间段内，可跨线路段比不可跨线路段更早出现跟驰行为.

表3 缓慢交通流坐标转换结果

由上文可知，基于速度的宏观聚类方法将交通流分为畅通、缓慢和拥堵3个状态.相对速度法又将缓慢交通状态划分为自由流和跟驰状态.因此，本文将交通流分为四个状态，分别为畅通自由流、缓慢自由流、缓慢跟驰、拥堵跟驰.见表4.

表4 主干路交通状态划分

3 对比分析

3.1 基于微观交通流理论的车头时距方法

基于微观交通流理论的车头时距法中，选择相对速度绝对值法进行比较.图5为按照车头时距划分的2状态结果.任一数据点与原点所连直线的斜率表示当前流量、密度下的速度.直线斜率越大，说明交通流的速度越大.实际交通中，当交通流为自由流时，密度随着流量的增加而增加，由于车辆之间的相互影响较小，因此速度变化较小；当交通流为拥堵状态时，密度继续增加，车辆之间的相互影响增大，速度和流量随着密度的降低而降低.在图5中每条道路出现两处与真实交通流不符的现象.如图5中黑圈Ⅰ中的交通流速度极高，却将这部分交通流划分为跟驰；黑圈Ⅱ中的交通流密度极高，速度相对较小，却将交通流划分为自由流.说明相对速度绝对值法会将自由流中前后车辆距离较近的交通流划分为跟驰，例如，早高峰之前，流量尚未达到拥挤流时，路段上游交叉口等待的车辆在绿灯放行后，车流中车辆之间间隔较近，但此时，交通流为自由流.在拥堵状态时，拥挤的车辆由于路段下游交叉口绿灯的放行使得路段较空，车辆以较大的车头时距通过路段，从而将交通流误判为自由流.因此，基于微观交通流理论的车头时距法适用于高速公路等非阻断交通流，在城市主干路上的应用效果较差.

图5 基于车头时距划分的交通流状态划分结果

3.2 基于宏观统计理论的聚类方法

对速度采用k-means法聚类得到的3～6个状态流量-密度，如图6所示.由图6可见：当交通状态数大于3时，自由流均被分为两个状态，两个状态数据分布在两条夹角很小的区域内且交替出现，无法达到聚类对同簇数据差异最小的要求.实际交通中，密度随流量增大而增大，交通流状态应逐步过渡，不应出现交通状态近似周期性交替的现象.此种情况的出现，可能是由于交通流受城市主干路信号灯管控导致的.

图6 基于k-means法的交通流状态划分结果

除自由流外，其他交通流状态的速度不重合，符合密度越大速度越低的实际情况.由此可知，聚类分析对拥挤状态划分的准确性较高.其中，基于宏观统计理论的聚类方法所得到的三状态分类效果最符合实际交通状态.

3.3 基于宏观交通流理论的三相位法

三相位法划分的交通状态流量-密度结果见图7.由图7可见，三相流理论将拥堵进一步划分为亚稳态同步流与稳定同步流，此结论与现有研究一致.亚稳态同步流与稳定同步流的速度范围基本重合.即同一个速度的交通流，可能是亚稳态同步流，也可能是稳定同步流.但实际交通流中，密度与速度线性相关，不应出现同一个速度对应两个交通状态的情况.

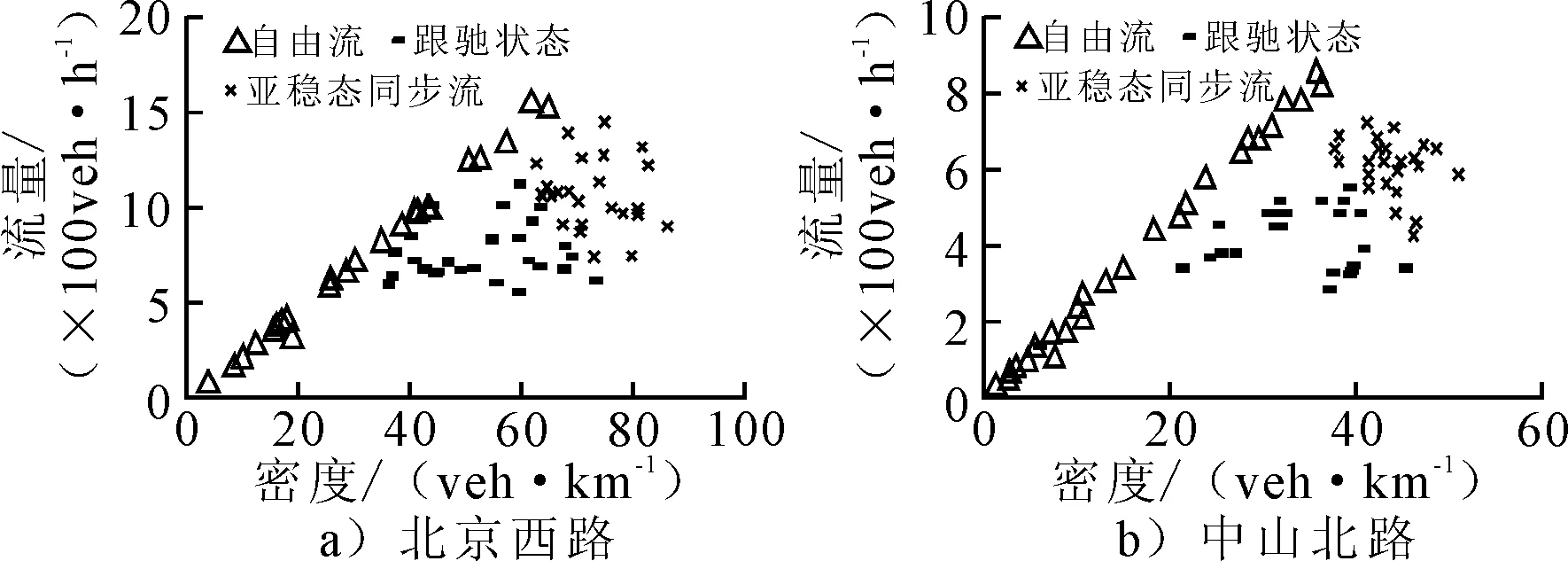
图7 基于三相位法的交通流状态划分结果

3.4 本文所提划分方法

本文所提方法将交通流划分为四个状态，分别为畅通自由流、稳定自由流、稳定跟驰和拥堵跟驰，其中，畅通自由流、稳定自由流均为自由流.分类结果见图8.图中K1～K4为从坐标轴原点画出的直线，其斜率分别表示各状态的速度阈值，由图8可以看出：

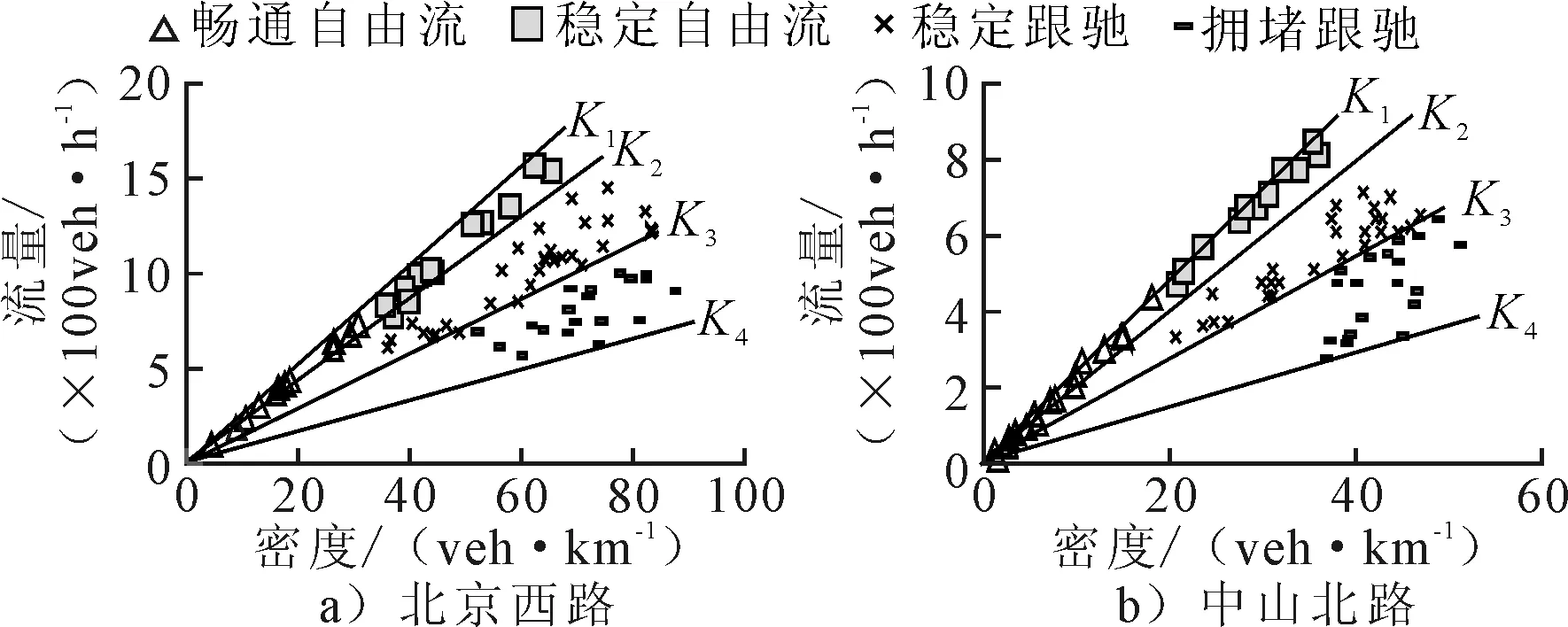
图8 本文方法划分的交通流状态

1) 畅通自由流状态下，车流速度快，密度低，所有数据近乎在同一条从坐标轴原点画出的直线上.该状态下所有点的斜率几乎大于其他状态下所有点的斜率.说明该状态下，车速近乎相同.此结论符合在低密度情况下，驾驶员自由驾驶，车辆几乎不受前后车辆影响的实际情况.

2) 稳定自由流状态下，车流速度与畅通自由流状态下的车流相比稍微降低.该状态下的所有数据不在同一直线上，而是在两条夹角很小的直线之间(K1与K2)，其中K1与自由流状态下数据描绘的直线近乎重合，K2位于此条直线下方.说明该状态下，随着流量的增加，车速稍有下降，道路依然保持畅通状态.

3) 稳定跟驰状态下，流量随着密度的增加而降低.该状态下，所有数据在K2与K3两条直线之间，且K2与K3夹角大于稳定自由流状态下K1与K2的夹角.说明在稳定跟驰状态下，速度降低幅度较大.这符合实际交通流中，当道路通行能力达到最大值后交通逐渐拥堵，车辆之间的影响加强的实际交通流情况.

4) 拥堵跟驰状态下，流量随着密度的增加继续降低.该状态的数据位于夹角最大的K3与K4两条直线之间.说明该状态下，速度、流量降低幅度最大.该情况符合在交通密度较高时交通开始阻塞，整条道路交通流呈现同步跟驰的交通流情况.

综上，本文将自由流分为畅通自由流、稳定自由流符合城市主干道受路段两端交叉口信控影响形成的阻断交通流运行特征.流量相对较少时交通处于畅通自由流阶段，信号灯可以较好地适应交通流的运行情况，车辆大概率可以不停车直接通过交叉口，且不受前后车辆影响；自由流流量增加到一定数量时处于稳定自由流阶段，路段上游交叉口出现少量等待绿灯放行的车辆，当绿灯亮起时，排队等待的车辆成群通过路段，但群内车辆之间的微小干扰使得车辆速度略微降低.除自由流外，稳定跟驰和拥堵跟驰两个状态的速度不重合，符合密度越大速度越低，密度与速度线性相关的实际情况.

4 结 束 语

本文设计了一种适用于城市主干路的交通流状态划分方法，该方法克服了现有方法只包含微观交通流信息或宏观交通流信息的不足.将主干路交通流划分为4个状态，分别为畅通自由流、稳定自由流、稳定跟驰和拥堵跟驰.与车头时距法相比，本文所提方法能有效区分自由流和拥堵流，不存在将拥堵流判断为自由流，自由流判断为拥堵流的情况.与k-means聚类方法将自由流划分为两个在自由流阶段交替出现的交通状态相比，本文划分的畅通自由流、稳定自由流更符合聚类同簇内的数据差异较小，不同簇内的数据差异较大的要求，与城市道路阻断交通流运行特征相符.与三相流相比，本文将自由流划分为畅通自由流、稳定自由流，该划分符合城市阻断交通流的运行特征，符合密度与速度线性相关的实际情况，且本方法能得到确切的交通流状态阈值.因此本文所提方法分类效果优于常用交通状态划分方法，能有效地对城市主干路交通流状态进行分类.未来将进一步验证本方法是否适用于城市次干路、无信号控制路段以及高速公路.