多过程耦合动力学数值模拟在热液矿床研究中的应用及发展前景

黄沁怡, 李增华, 许德如, 池国祥, 邓 腾, 赵朝霞, 于得水

多过程耦合动力学数值模拟在热液矿床研究中的应用及发展前景

黄沁怡1, 2, 李增华3, 4*, 许德如1, 4, 池国祥5, 邓 腾4, 赵朝霞1, 2, 于得水1, 2

(1.中国科学院 广州地球化学研究所 矿物学与成矿学重点实验室, 广东 广州 510640; 2.中国科学院大学, 北京 100049; 3.东华理工大学 江西省放射性地学大数据技术工程实验室, 江西 南昌 330013; 4.东华理工大学 核资源与环境国家重点实验室, 江西 南昌 330013; 5.Department of Geology, University of Regina, Regina S4S 0A2, Canada)

热液矿床的形成是一个复杂的多因素耦合过程, 包括传热、流体运移以及物质的传输和沉淀。近年来, 随着计算机技术和计算数学的发展, 多过程耦合动力学数值模拟在成矿研究中的应用越来越深入, 主要模拟成矿系统中的热传递、流体流动、构造变形和化学反应过程以及它们之间的相互作用。本文首先介绍了数值模拟的基本方法、常用的数值模拟软件及其应用范围, 其次总结了多过程耦合动力学数值模拟在热液成矿理论研究和成矿预测中的应用, 最后总结了数值模拟的优缺点并讨论其发展趋势。数值模拟是解决一些成矿问题的有效分析工具, 将会推动矿床研究从定性、半定量往定量的方向转变。

数值模拟; 数值模拟软件; 成矿作用; 耦合动力学

0 引 言

金属热液矿床的形成, 通常包括源区金属元素的获取及溶解、流体搬运以及在合适的场所沉淀聚集(图1)(Cox, 2005), 这一动力学过程十分复杂, 既包括物理过程, 如流体流动、热量传递和岩石变形等, 又包括化学过程, 如矿物溶解和沉淀、水岩反应等(Chi and Xue, 2011), 而且这些过程之间还有全反馈耦合, 如不同地质单元间的渗透性差异和局部的渗透率变化可以为矿物沉淀提供机制(Weis, 2014), 而矿物的沉淀也能影响岩石渗透率, 反过来影响流体的运移速度(Hobbs et al., 2000)。另外, 成矿系统一般都具有巨大的时空尺度特点, 因此, 利用传统地学研究方法, 在实验室内对成矿动力学过程进行研究具有一定的局限性(Elder, 1967; Sondergeld and Turcotte, 1977; Menand et al., 2003; Emmanuel and Berkowitz, 2006, 2007)。

数值模拟技术在矿床动力学研究方面具有一定的优势(Chi and Xue, 2011), 常见的模拟研究包括流体运移(Cline et al., 1992; Griebel et al., 1998; Yang et al., 2004)、构造变形(Sorjonen-Ward et al., 2002; Lin et al., 2006; Zhang et al., 2011)、热传递(Zhao et al., 1998, 2000, 2006; Andersen and Weis, 2020), 以及化学反应(Aghbelagh and Yang, 2014; Zou et al., 2019), 对这些因素的研究有助于理解与成矿相关的流体动力学过程(Yapparova et al., 2019)。近年来, 随着计算机技术的发展, 数值模拟技术在成矿过程动态化和定量化的研究中越来越普遍(Hobbs et al., 2000; Cooke and McPhail, 2001; Oliver et al., 2006; 周叶, 2007; Chi and Xue, 2011; 赵义来和刘亮明, 2011; 张嵩松, 2011; 贾蔡等, 2014; Zhao et al., 2018; 李增华等, 2019; 戴文强, 2020; Takahashi et al., 2020)。理想情况下, 热液系统中多相流的数值模拟可能会成为研究瞬态过程的常规工具(Driesner and Geiger, 2007)。本文通过总结多过程耦合动力学数值模拟的基本理论, 结合其在热液矿床研究中的应用实例, 探讨数值模拟在矿床研究方面的应用, 并提出其存在的问题及今后的发展方向。

1 数值模拟方法

1.1 成矿动力学过程的数学表达

深刻认识矿床的成因机制和成矿规律能为成矿预测提供依据。矿床的形成是热力场、流体场、应力场以及化学场耦合作用的结果(Hobbs et al., 2000)。研究矿床成矿过程, 最理想的状态就是将物理和化学过程结合起来进行研究, 因此对热力场‒流体场‒应力场‒化学场(THMC: thermal-hydraulic-mechanical- chemical)耦合作用的研究至关重要(图2)。

成矿过程中, 流体流动起到了关键性的作用, 所以对成矿系统中流体流动的研究是建立成矿模式的重要因素(Chi and Xue, 2011)。成矿流体流动通常伴随着岩石变形和热量的传递, 因此流体流动(质量守恒)方程需要与热量流动(热能守恒)方程和岩石变形(介质连续)方程耦合。此外, 由于化学反应(矿物溶解与沉淀)可以改变岩石的孔隙度和渗透率, 进而影响流体的流动, 所以质量平衡方程也需要与化学反应有关的方程耦合(Hobbs et al., 2000; Chi and Xue, 2011)。

在耦合体系中, 由应力场引起的构造变形是成矿最基本的因素之一。大型构造的形成和演化控制着有关的沉积、岩浆、变质和流体作用。在岩石圈尺度, 深部构造可驱动深部流体活动, 而流体与围岩相互反应制约着热液成矿系统的形成和演化。在矿田尺度, 不同的构造样式可控制矿床的分布以及矿体的形态和产状。在不同的构造应力背景下, 成矿的热动力条件以及物理和化学条件均有所不同, 形成不同的流体循环方式、水岩反应强度、蚀变规模与类型等(邓军等, 2001; 席先武等, 2003)。而构造变形会引起岩石体积的变化, 进一步改变岩石的渗透率和孔隙度等物性参数, 变形本身也可以造成局部或区域性的流体势梯度, 为流体运移提供动力并且创造通道。同时热液流体的运移可以改变周围岩石的温度, 并通过与周围岩石反应、水解等来弱化、降低岩石强度以及矿物颗粒间的摩擦系数, 进而影响岩石的力学性质, 从而影响岩石的变形与破坏。而温度对成矿作用的影响体现在温度的改变会导致流体密度、黏度的变化, 甚至使流体发生相变。反之, 流体流速的改变也会引起温度发生一定的变化。

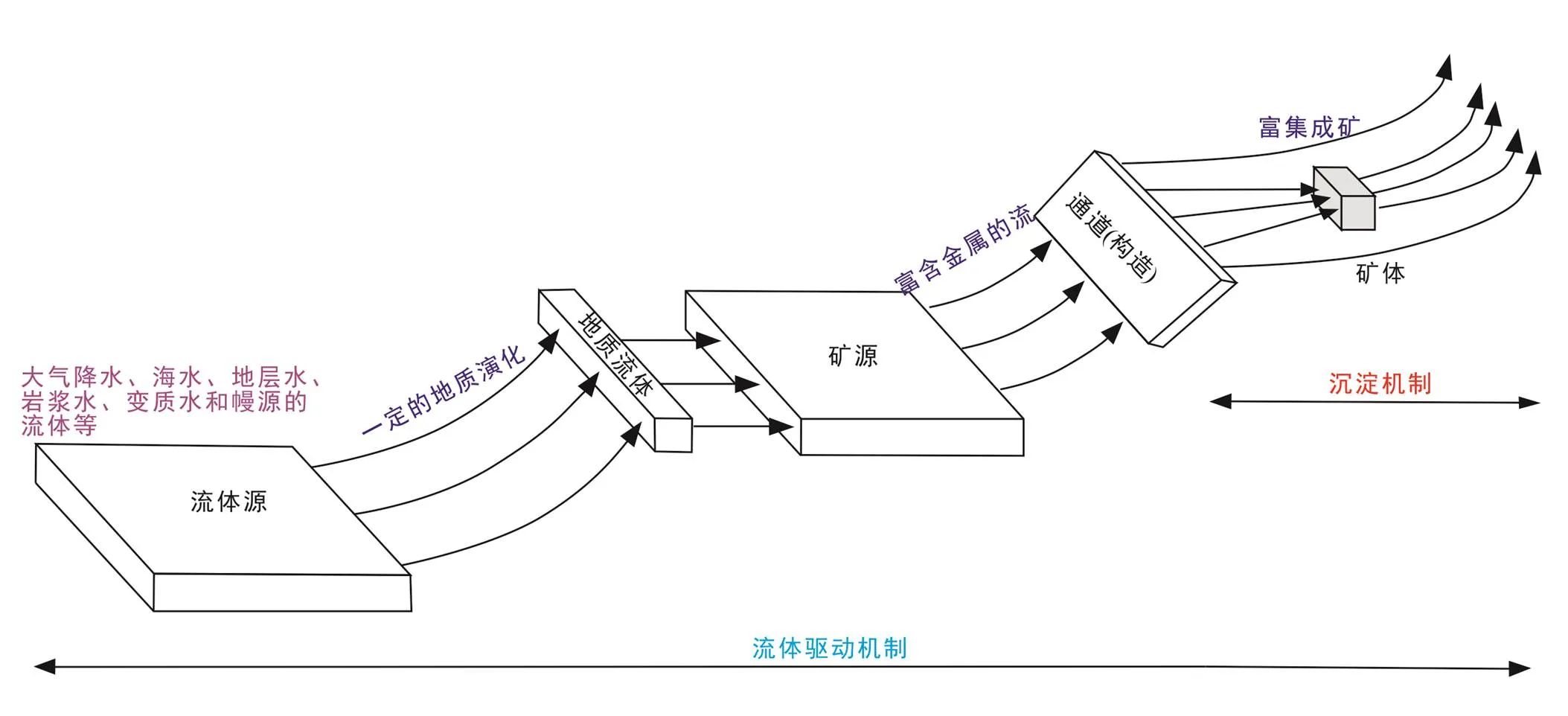
图1 热液成矿系统及其演化示意图(据Cox, 2005修改)

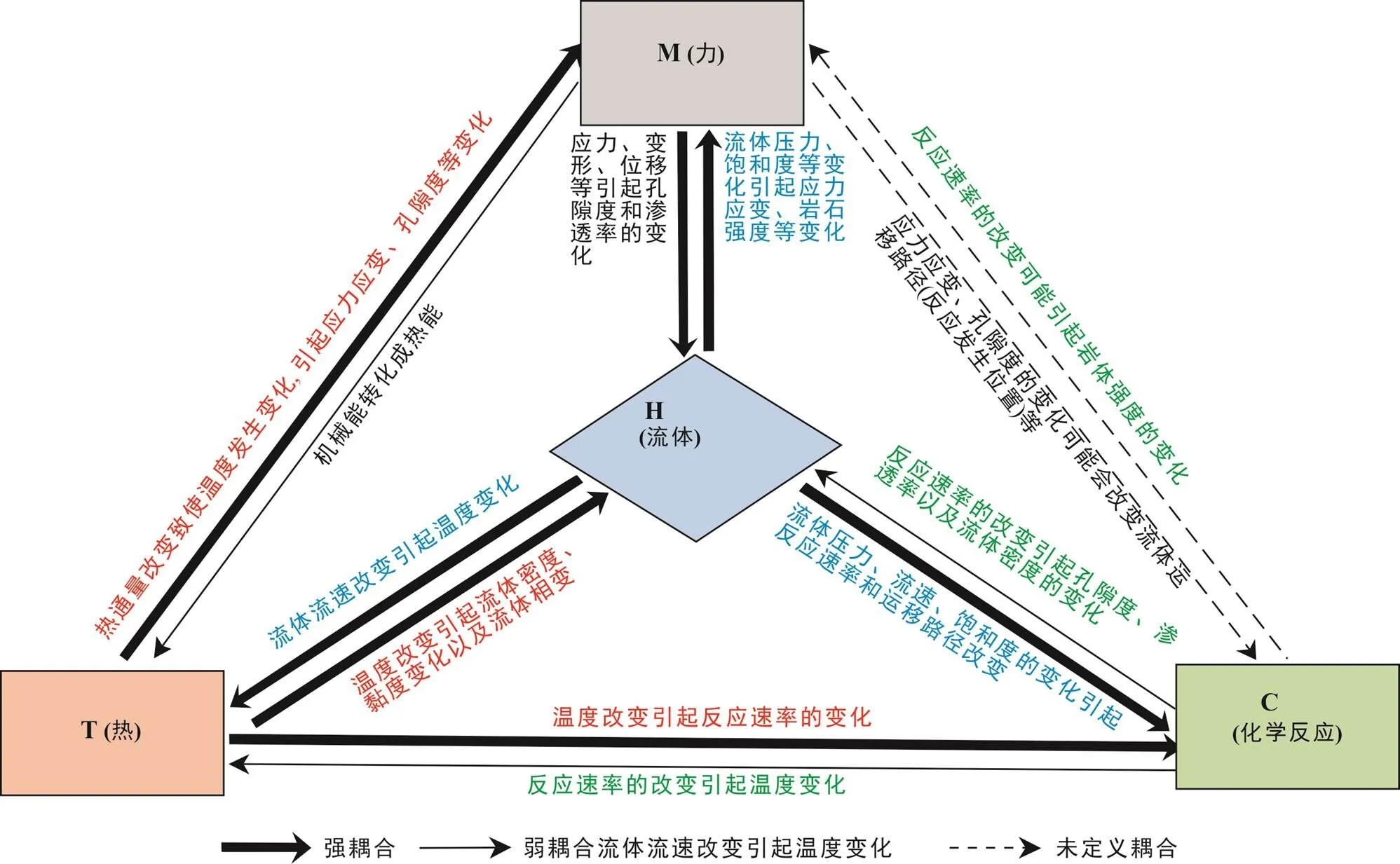
图2 THMC耦合机制示意图(据Hobbs et al., 2000; Jing and Feng, 2003修改)

因此, 热液矿床矿体的最终产出状态与位置实际上是热(T: thermal)‒流体动力(H: hydraulic)‒应力(M: mechanical)‒化学反应(C: chemical)(THMC)之间耦合的结果(图2)(贾跃明, 1996; Jing and Feng, 2003; Joshua et al., 2009; 戴文强, 2020)。这四个过程之间相互耦合加强使得矿化速率得到优化, 进而形成矿体(Hobbs et al., 2000)。

对THMC四个过程的刻画是通过一系列的偏微分方程来实现的, 包括达西定律、应力应变方程、热传导方程、能量和质量守恒方程等(Hobbs et al., 1976; Jaeger and Cook, 1979; Garven and Freeze, 1984; Vermeer and DeBorst, 1984; Mandl, 1988; Ord, 1991; Ord and Oliver, 1997; Oliver et al., 2006; Cui et al., 2012; Ingebritsen and Appold, 2012)。

1.2 数值计算常见方法和模拟软件

由于地质复杂性和边界条件的设置, 基本不可能求得成矿过程的偏微分方程的解析解, 因此偏微分方程只能通过数值方法来求解。目前在地质领域常用的数值计算方法有六种, 分别是有限单元法(Finite Element Method)、有限差分法(Finite Difference Method)、积分有限差分法(Integral Finite Differences Method)、离散单元法(Discrete Element Method)、控制体积有限元法(Control Volume Finite Element Method)和有限体积法(Finite Volume Method) (Narasimhan and Witherspoon, 1976; 王勖成和邵敏, 1988; 王仁, 1994; Aavatsmark, 2002; Lee et al., 2002; Weis et al., 2012)。

根据解决地质问题的不同, 所选用的数值模拟软件也会有差异。如美国Itasca公司开发的FLAC软件(Fast Lagrangian Analysis of Continua, 包括2D和3D), 常用于模拟涉及岩石构造变形的问题, 还可进行与热力场和流体场的耦合研究, 在矿床学中常用来研究构造变形与流体运移的耦合过程(刘波和韩彦辉, 2005; Liu et al., 2005; Zhang et al., 2006, 2011; Liu and Dai, 2014)。

FEFLOW(Finite Element subsurface FLOW system)是由德国水资源规划和系统研究所于20世纪70年代末基于有限单元法开发的用于模拟地下水流和污染物运移的专业软件, 能够模拟多孔介质中饱和、不饱和地下水流以及溶质运移和热量运移过程。它不考虑构造变形, 主要研究流体和热的耦合作用(Diersch and Kolditz, 1998), 可以模拟多孔介质和裂缝介质中的地下水流动、传质和传热, 主要用来研究各种流体对流系统(Diersch, 2002; Cui et al., 2010; Ju et al., 2011)。

MODFLOW(Modular Three-dimensional Finite- difference Ground-water Flow Model)是美国地质调查局于20世纪80年代开发的一套用于孔隙介质中地下水流的三维有限差分数值模拟程序, 主要用于模拟现代地下水的流动(McDonald and Harbaugh, 1984; Sanford, 1994; Harbaugh, 2005)。由于其模块化的结构以及多样化的求解方法为结合其他模拟性能提供了一个稳健的结构, 现已成为最为普及的地下水运动数值模拟的计算软件。

Basin2是用来研究贯穿地质时期的沉积盆地中地下水流体系变化过程的软件(Bethke et al., 1993, 2007)。可研究沉积盆地的古地温史、压力场、流场、有机质热成熟度等的变化, 常应用于与沉积盆地相关的成矿系统中(Bethke, 1986; Chi and Savard, 1998; Chi, 2001; Chi et al., 2006, 2010; Xue et al., 2010, 2011)。

TOUGH2(Transport of Unsaturated Groundwater and Heat)是由美国劳伦斯伯克利国家实验室开发的用于模拟多组分多相流的软件(Pruess, 1991), 具有对孔隙和裂隙介质中水流和热运移的强大模拟能力。TOUGHREACT是在TOUGH2基础上, 用于模拟孔隙裂隙介质中多相流体非等温流化学反应的软件, 采用积分有限差分法来模拟地下多相流体运动和地球化学运移耦合过程与机理。在CO2地质储存、地热能的开发、核废料的地质处理等领域应用广泛(Xu et al., 2004, 2006), 现已用于各种热液系统中, 包括地下水流在内的多相、多组分的问题(Todesco et al., 2003; Mannington et al., 2004)。

PFC(Particle Flow Code)软件是由Itasca公司开发的颗粒流分析程序(Itasca, 2002), 目前有二维和三维两种, 该软件属于离散元范畴。与传统的基于网格的数值方法不同的是, 它是通过离散单元法来模拟由许多单个圆形颗粒单元集合而成的岩石域, 例如可用于模拟露头尺度矿化脉结构的发展(Zhang et al., 2011)。

CSMP++(Complex System Modelling Platform)是由苏黎世联邦理工学院和伦敦帝国理工学院的研究小组开发的模拟平台, 采用的是控制体积有限元方法, 能够模拟热液系统中的气液相分离和运移。Driesner et al. (2015)介绍了该软件的技术特性及其在研究超临界和岩浆环境下的地热系统的应用实例。CSMP++现已成功应用于与斑岩铜矿形成(Weis et al., 2012)、超临界和高焓地热源(Scott et al., 2015, 2016)以及岩浆侵入体上方的地热盐水沸腾(Scott et al., 2017)等相关的热液流体问题。CSMP++GEM耦合代码可以模拟两相沸腾热液系统中的流体流动和基于焓的热传导, 以及溶质运移和化学反应(Yapparova et al., 2019)。

FEHM(Finite Element Heat and Mass Transfer Code)是为模拟地热和干热岩储层而开发的计算机程序, 它采用有限单元法求解多孔渗透介质中多相流的传热传质方程。

FISHES(Fully Implicit Seafloor Hydrothermal Event Simulator)采用的是有限体积法, 能够模拟NaCl-H2O体系中两相流体的流动。其所使用的状态方程最高只能应用于800 ℃的温度(Lewis, 2007)。

HYDROTHERM采用有限差分法模拟三维多相地下水流和相关的热传递。它可以处理高达1×109Pa (104大气压)的高流体压力和高达1200 ℃的高温问题, 但只能模拟单一流体成分的地下水流动(Kipp et al., 2008)。

2 多过程耦合动力学数值模拟应用现状

如前所述, 解决复杂的成矿过程, 实现热‒流‒应力‒化学等四个场(THMC)的耦合, 数值模拟是最为理想的。但是由于数值模拟软件的限制, 目前在矿床学的实际研究中, 根据研究的矿床类型和实际地质情况, 采取的模拟场可能是单一的(如只有流体场)(Bethke, 1985; Xue et al., 2011; Chi et al., 2013)或者多个(McLellan et al., 2004; Schaubs et al., 2006; 鞠明辉, 2011; 贾蔡等, 2014; 赵鹏飞等, 2017; 陈亮等, 2018; 闵令帅等, 2020), 四场(THMC)耦合的模拟在矿床学中的应用并不多见(Zhao et al., 2000; Taron and Elsworth, 2009; Taron et al., 2009; Poulet et al., 2010)。本文主要以研究较多的热液矿床为例, 讨论多过程耦合数值模拟在矿床学中的应用。

2.1 数值模拟在热液矿床成矿理论中的应用

2.1.1 密西西比河谷型矿床

产于沉积环境中的矿床如密西西比河谷型(MVT)铅锌矿床、沉积型块状硫化物矿床(SMS)和板状铀矿床大多是在没有明显局部同期构造变形的情况下形成的(Ingebritsen and Appold, 2012)。所以对于这种类型矿床的数值模拟着重考虑的是流体对于成矿的影响, 而一般不考虑力学变形的作用。下面以MVT矿床为例讨论数值模拟的应用。

MVT矿床是在50～250 ℃条件下从稠密的盆地卤水中沉淀形成的, 是与岩浆活动无关或者无直接相关的浅成后生层控矿床(Leach and Sangster, 1993)。证据表明, 区域尺度的流体流动是MVT矿床形成的重要机制。Sharp (1978)利用一维模型对Arkansas州北部Missouri东南地区Ouachita盆地进行了模拟, 结果显示采用合理的断层和含水层水力传导率, 大量的流体可以迅速迁移到Ozark穹丘附近的露头区域, 表明铅锌矿化可能是由于盆地内热的孔隙流体多次进入形成的。Bethke (1985)研究了克拉通内沉积盆地演化过程中沉积压实造成的流体超压的作用, 流场模拟结果显示沉积盆地在演化过程中并未发生显著的流体超压, 深部流体倾向于向两侧运移, 而近地表流体往上运移, 该结论对于认识盆地内次生石油运移、卤水渗透富集和密西西比河谷型矿床的形成具有重要意义。Appold and Nunn (2005)研究了Ouachita造山运动末期Arkoma盆地抬升过程中的流体流动对密西西比河谷型铅锌矿形成的影响, 结果显示地形驱动是地下水流动的一个重要机制, 而Arkoma盆地深部压实作用产生的超压在隆起早期贡献较小。

这些研究表明数值模拟在探究MVT矿床形成过程中流体流动的驱动机制和路径方面发挥了重要作用。但是除了浅部的重力驱动流体对流系统之外, 还有深部可能存在的热和构造作用所产生的影响, 更复杂的矿床成因模型还需要通过定量耦合过程建模进行测试。

2.1.2 不整合面型铀矿床

不整合面型铀矿床受切穿不整合面的基底断层控制, 但其成矿流体的动力学机制一直存在争议, 不同学者通过多过程耦合模拟的方法, 对此展开了深入研究。Chi et al. (2013)对加拿大Athabasca盆地演化过程中不平衡压实作用下的超压情况进行了流体场的数值模拟, 结果表明, 在整个沉积史上, 盆地内未发现明显的流体超压, 且沉积压实驱动的流体流动非常缓慢, 温度剖面不受干扰。Cui et al. (2010)通过热‒流耦合模拟, 显示盆地地层中发生的自由对流对铀的运移起到重要作用, 而最大流速在不整合面附近这一模拟结果也符合铀在不整合面附近聚集的事实。Li et al. (2016)继续研究了加拿大Athabasca盆地基底断层对盆地热对流系统的控制作用, 发现基底断层的位置、间距、产状和热导率对热对流发生的位置和对流圈的大小有影响, 其影响程度取决于断层在模型中的热导率和相对位置, 盆地流体可以沿断层进入基底然后再返回盆地, 这一发现对认识不整合面型铀矿的成矿模式有重要意义。

针对不整合面型铀矿受基底断层控制的现象, 不同学者研究了构造变形对流体运移的控制作用。Cui et al. (2012)利用FLAC 3D软件模拟了挤压和拉张应力条件下的流体运移机制, 发现挤压背景下流体可通过基底断层进入砂岩盆地内, 而在拉张应力条件下流体可从盆地沿基底断层流入基底。针对这些断层均为逆断层的特点, Li et al. (2017)专门研究了在挤压环境下, 基底断层发生活化而引起的流体流动方向变化的问题, 结果表明流体流动方向取决于挤压的程度: 在挤压程度相对较低时流体可以沿着断层流出基底进入盆地, 但当挤压程度相对较高时, 基底断层切穿不整合面的位置发生扩容, 导致流体从盆地沿断层进入基底, 这说明在不同构造变形阶段下, 不同流动方向的流体所形成的矿体可以存在于同一个断层系统中, 这对于找矿是一个新的指示, 可以根据变形程度来寻找砂岩内或基底内的矿床。同时, 对比盆地内不同矿床的数值模拟能够发现, 基底的岩性差异会控制扩容区的产生位置以及流体运移的方向和速率, 最终控制矿体产出的位置(Li et al., 2018a, b)。李增华等(2019)认为活化断层不仅为流体提供流动通道, 还提供了部分驱动力。Li et al. (2020)对挤压应力、热以及流体的耦合作用进行了研究, 从而评价变形驱动流体流动与热驱动流体对流之间的关系以及它们对铀矿化的相对重要性, 其研究结果表明, 相对较高应变率的构造挤压能够瞬间破坏盆地内已形成的热对流, 而随着时间的推移、变形的进行和超压的减弱, 对流可能重新出现; 相比之下, 低应变率的构造挤压对已经形成的热对流没有影响, 且基底内变形驱动的流体流动与盆地内的热驱动流体对流共存, 模拟结果说明在与远场构造事件有关的构造活跃期, 基底断层的挤压活化使其渗透率增大, 并导致流体向伴随个别地震事件形成的剪胀带处流动, 然而在构造静止期, 流体流动模式以热对流为主。

当重点考虑热和流体流动与化学反应之间的关系时, 可进行THC耦合数值模拟。Aghbelagh and Yang (2014)采用TOUGHREACT软件, 研究石墨断层带对不整合面型铀矿形成的影响, 建立了有甲烷和无甲烷的两种模型, 结果显示在有甲烷的模型中, 矿体主要产出在不整合面附近, 而在无甲烷的模型中, 矿体主要在不整合面以下的断层带远端出现, 并且沉淀时间较长, 体积分数较低, 其中物理化学参数如氧逸度和温度对于铀矿的沉淀位置有着很大的影响, 在不整合面以下沉淀的铀矿与氧逸度的降低有关, 一般是因为氧化性的含铀流体与还原性物质发生了相互反应。

2.1.3 斑岩型矿床

斑岩型矿床形成于近岩浆环境中, 许多金属元素从硅酸盐熔体中被提取出来, 并由岩浆热液输送到成矿部位。在这个过程中, 时间也是影响矿床成因的重要参数。Vigneresse et al. (2019)建立了一个金属从熔体扩散到岩浆挥发相(MVP)过程的动力学模型, 并计算了不同金属(Cu、Au、Ag、Mo、W、Sn)的富集因子, 研究结果表明, 岩浆房的快速充填和长时间的侵入期是形成斑岩型矿床的必要条件。在该类矿床形成过程中, 活性岩浆流体在温度和化学成分上都有较大的梯度(Sillitoe, 2010), 所以热和化学也是模拟需要考虑的重要因素。Ague and Brimhall (1989)利用流体动力‒化学反应耦合模拟方法对斑岩铜矿床的表生富集过程进行了研究, 模拟表明, 氧含量是成矿系统的关键控制因素, 矿石矿物沉淀的主要硫源来自原矿石带中的含硫矿物, 而不是从淋滤带迁移来的硫酸盐。依据Geiger et al. (2002)建立的蒙大拿州Butte斑岩铜矿中热液脉形成的流体动力‒化学反应耦合模型, 厘米尺度的绢云母蚀变包壳仅需要几十年就能形成, 它是由脉中流动的岩浆液扩散增加的钾离子和氢离子所形成。Eldursi et al. (2009)通过热‒流耦合数值模拟, 认为侵位深度是控制对流散热区的范围和几何形状的关键物理参数, 而浅层顶部作为对流流体和矿化带的聚集点, 改变了流体流动的模式, 他们认为由花岗岩侵位引起的对流作用是花岗岩型金矿形成的主要原因, 并且该类型矿床的形成受侵入体周围断裂热晕的控制。Yapparova et al. (2019)采用CSMP++GEM耦合代码对Butte岩浆热液系统进行了热‒流‒化学过程的耦合数值模拟研究, 并与TOUGHREACT和OpenGeoSys- GEM的模拟结果进行比较, 结果吻合较好, 但CSMP++GEM耦合软件可以执行反应传输模拟热液条件下(600 ℃, 100 MPa)的水岩相互作用, 包括非理想固溶体(如斜长石和碱长石), 这是其他反应传输软件所做不到的。斑岩型矿床所特有的蚀变分带对于研究其形成过程有一定的帮助, 在不同的斑岩系统中, 蚀变分带会有所不同, 这取决于成矿流体体系的性质及发育程度、产出的构造环境、岩体和围岩性质及后期剥蚀程度等, 也可利用数值软件来模拟不同流体体系下的斑岩系统, 从而研究其异同之处。Weis et al. (2012)将岩浆流体的排出与岩石渗透率的瞬态演化和两相流的动力学联系起来, 对斑岩系统的水文情况进行了模拟, 其研究结果表明, 在静岩压力下上涌的热岩浆流体与静水压力下的冷大气流体对流的边界处, 响应岩浆流体排出的动态渗透率能够使金属稳固沉淀。

2.1.4 矽卡岩型矿床

矽卡岩矿床既可由接触作用形成, 也可由区域交代作用形成。世界上绝大多数重要的矽卡岩矿床基本都产于中小型不整合火成岩侵入体的接触带, 并被认为主要或完全与侵入体释放的岩浆热液有关(Misra, 2000)。在接触带这种特殊环境中沉淀成矿, 其动力学环境需要满足两个条件, 即存在新的扩容空间和有序的动力条件(热与构造变形)(刘亮明等, 2008)。汇流与扩容之间存在着重要的相互关系, 在应力集中区容易发生岩石破裂形成新的扩容空间, 从而引起流体汇聚, 而随着流体的增加, 流体压力也会增大, 进而诱发水压致裂, 再一次使得流体汇聚, 如此往复循环, 并在一定的化学条件下沉淀成矿。刘亮明等(2008)以凤凰山铜矿和安庆铜矿两个典型的矽卡岩矿床为例, 模拟岩体主体基本固结并形成了早期矽卡岩后的退化蚀变和热液成矿的物理过程, 探讨了岩体冷却过程中汇流扩容空间的形成及其对矽卡岩矿床的控制, 并分析了汇流扩容空间控矿模式对深部找矿的意义。Liu et al. (2010, 2012, 2016)分别对安徽安庆矽卡岩铜矿区和广西大王顶金矿区进行了构造控矿规律数值模拟研究, 通过建立构造‒热‒流体成矿体系的三维数值模型, 确定侵入体冷却过程中成矿流体及温压条件和热液演化过程。戴文强(2020)利用数值模拟方法研究了安庆铜矿热液蚀变及成矿过程, 结果显示温度驱动流体流动下的成矿物质空间分布特征与实际矿体形态特征更吻合, 表明安庆铜矿形成过程可能以温度驱动的流体运移为主。张婉秋和邹艳红(2020)采用TOUGHREACT软件对虎头崖铅锌多金属矿床进行成矿过程化学反应数值模拟研究, 探究不同温压条件下成矿元素化学平衡浓度变化的趋势, 并考虑其对闪锌矿和方铅矿矿物溶解沉淀情况的影响, 模拟结果表明, 不同温度和压力对成矿元素化学平衡浓度影响不同, 温度是控制方铅矿和闪锌矿沉淀的核心因素, 其中方铅矿的最佳成矿温度范围为155～250 ℃, 闪锌矿为100～300 ℃, 压力对其沉淀的影响不大。在矽卡岩型矿床的成矿过程中, 引起热液流动的动力除了温度梯度和压力梯度之外, 浓度梯度也是比较重要的影响因素。胡训宇(2020)对麻姑山矽卡岩型铜钼矿床进行了多过程耦合数值模拟, 假定流体与灰岩地层发生反应并在接触带及其附近生成石榴子石, 结果显示在向斜两翼岩体与地层接触带均有矽卡岩典型矿物石榴子石生成, 且位于向斜北西翼的低浓度石榴子石比位于南东翼麻姑山矿床的要多, 但其高浓度石榴子石却比南东翼的要少, 说明该地区向斜北西翼也具有一定的成矿潜力, 但可能没有已探明的麻姑山矿床大。在矽卡岩矿床形成的交代过程中, 浓度梯度会随着反应带厚度的增加以及交代作用的停止而减小。这一方面, 还需进一步的模拟研究。

2.2 数值模拟在成矿预测中的应用

实现科学找矿的重要方法是进行成矿预测, 需要寻求可以达到成矿预测过程客观化、预测结果最优化、预测精度定量化的途径(赵鹏大, 2007)。数值模拟的目的是理解成矿的因果过程, 首先是确定成矿的主导过程, 然后研究这些过程对矿石的形成可能产生的影响, 而一旦确定了这些因素, 就可以利用三维建模分析或野外观察结果进行预测和勘探(Vigneresse, 2019; Vigneresse and Truche, 2020)。如任梦依(2016)利用FLAC 3D软件模拟印度洋中脊研究区多金属硫化物的成矿过程, 并结合Surpac软件的三维建模结果, 开展了西南印度洋龙旂热液区双向预测评价, 提高找矿概率。

Liu et al. (2011, 2012)在安庆矿田地质和地球物理资料的基础上, 采用数值模型模拟了与成矿有关的侵入体同构造冷却过程中的耦合地球动力学过程, 模型的计算结果表明, 不同来源的孔隙流体都集中在剪胀区, 且这些剪胀区与侵入体接触带的形状密切相关, 这意味着对深部矿床的勘探应以靠近侵入体接触边界的深部剪胀区为目标, 并根据这一模拟结果圈定了找矿靶区。

Hu et al. (2020)采用数值模拟的方法, 确定了传统分析方法难以识别的茶亭铜金矿床成矿系统的主要特征, 其中包括成矿事件的持续时间, 模型将传热、应力、流体流动、化学反应和物质迁移联系在一起, 模拟出了与已知矿化分布相匹配的矿化区域, 并预测出矿床−1800 m以下具有潜在矿化带, 以及计算出茶亭矿床的形成持续时间为9600～75000 a。这些模拟结果不仅可用于深入了解斑岩型铜金矿床的成因、持续时间和斑岩成矿作用特征等, 也可用于未来进一步的建模工作和深部找矿勘探。

利用数值模拟对矿床进行预测时, 可以采用两阶段建模的方法: 首先建立多个模型反演矿区的矿体情况, 选出与真实地质条件最接近的一个模型, 这一阶段可以帮助我们较为准确地理解成矿的过程和控制因素; 其次通过利用这个最优模型来指导隐伏矿床的预测。这种方法可应用于具有已知矿床的区域, 然后使用从模型中获得的信息, 对新的或者更大的区域进行进一步的成矿预测(Zhang et al., 2011)。如Zhang et al. (2011)对广东阳春石菉铜矿成矿流体及构造变形进行了数值模拟实验, 根据所建立的二维离散变形模型以及连续介质变形‒流体耦合模型的模拟结果, 研究控制石菉铜矿脉体特征形成的关键结构因素, 并且证实了模型预测的成矿区域与实际成矿带的位置具有一致性, 可以用来帮助找矿。

基于数值模拟的勘查方法也在不断涌现。如Li et al. (2019)提出了一种基于三维数值模拟的勘探建模方法, 该方法集成了三维数值模拟、三维地质建模、三维地球物理建模和三维空间分析方法, 将概念或经验知识转化为三维成矿预测图, 最终圈定了安徽月山矿田深部隐伏矿化的多个勘探目标。其所建立的三维找矿模型不仅清晰地识别了已知矿化区, 而且有效地圈定了月山矿田深部矽卡岩型铁铜矿化的新靶区, 突出了该地区未来勘探的潜力。此外, 对结果数据的分析表明, 数值模拟方法可以为矿产勘查提供额外的预测信息, 这预示着数值模拟方法对未来三维建模技术在勘探方面的发展和使用具有重要的作用, 该方法可以有效提高成矿预测结果的预测能力, 不仅为下一步的勘探工作提供了智能化的数据支持和分析指导, 也为找矿预测提供了新的科学方法和强大的技术支持(周永章等, 2021)。

3 存在问题和发展趋势

数值模拟是研究成矿过程的重要工具, 可以量化有利于矿床形成的地质因素(Ord and Oliver, 1997; McLellan et al., 2004; Schaubs et al., 2006; Chi et al., 2013, 2014; Li et al., 2017; 陈亮等, 2018)。但现阶段的数值模拟还不能完全重现完整的成矿过程。如对于岩浆热液成矿作用, 目前无法模拟岩浆的凝固和热液的分异过程, 不能模拟气液相分离, 且对于开放的热液体系研究较少。对于断裂控制的热液成矿作用, 也没办法模拟岩石的破裂和愈合过程。尽管如此, 数值模拟为研究在不同地质环境中流体系统的运行方式仍然提供了有价值的见解, 其中包括量化可能的驱动机制、流体流动的速率和路径、矿石矿物的沉淀机制、热液系统的寿命、热液流体获得其温度和成分的机制, 以及渗透性和其他岩石性质对热液流体行为的控制效应等(Ingebritsen and Appold, 2012)。数值模拟作为一个研究方法, 具有不可比拟的优势, 不仅可以再现巨大时空尺度下成矿过程中主要因素的动态变化, 还能反演出测试分析可能无法得到的局部地区的地质特征, 且具有低成本试错的特点, 这是其他研究方法如室内实验分析以及传统地质研究方法所不具备的。

探索成矿元素聚集‒运移‒沉淀过程是研究成矿流体系统演化的主要目的, 其中包括成矿流体的运移、构造‒流体耦合作用和与成矿元素聚集‒沉淀有关的成矿流体自身演化特征(邓军等, 2005)。在矿床研究中, 定性和定量地了解矿床的形成过程中不同成矿因素发挥了何种作用, 多过程耦合的动力学数值模拟无疑是最理想的工具。但多过程耦合作用的模拟有一些问题仍未完全解决, 包括以下几个问题:

(1) 模型构建及其精度的问题。当涉及复杂地质体时, 需要考虑的因素很多, 比如模型尺度、单元类型、网格划分等。当建立的模型较复杂, 网格划分较细, 就会面临计算量过大的问题, 所需要耗费的计算时间也会成倍增长。而模拟耦合的过程越多, 也会增加计算的复杂度。为了提高计算效率, 可以考虑进行并行化计算。将地质问题分解成多层次的并发性子任务, 进行网格分区, 使各个区域进行独立计算, 再利用消息传递通信完成分区之间的任务并行和存储共享, 即实现了多层次的并行计算方法(徐传福等, 2020)。

(2) 受制于模拟软件的特点, 无法还原成矿过程中的真实物理化学条件。如目前很难在反应传输模型中实现大范围温压条件下的热‒流‒化学耦合, 许多软件限制了温度压力的范围, 如TOUGHREACT中饱和水蒸汽压力下的温度限制为300 ℃(Xu et al., 2004), 并只能模拟不可压缩单相流(如Open-GeoSys- GEM), 也根本无法模拟固溶体(如Geochemists’ Workbench)(Yapparova et al., 2019)。为了解决这些问题, 需要不断改进我们模拟多相系统中耦合热液流体流动、变形和反应传输的能力(Ingebritsen et al., 2010)。所以对软件的性能进行拓展或者是开发出更适用于大范围温压条件的软件和程序, 是实现复杂物理化学条件下的多过程耦合动力学数值模拟, 甚至是THMC全耦合数值模拟的必经之路。由于现阶段没有任何一个软件能进行THMC全耦合计算, 采用多软件耦合计算来完成对THMC耦合过程的模拟也是近期研究的一个发展趋势。Zhao et al. (2000)采用有限差分软件FLAC和有限元软件FIDAP建立耦合THMC模型, 考虑了不平衡化学反应的温度相关反应速率, 开发了求解可变形流体饱和多孔介质中的材料变形、孔隙流体流动、传热和化学反应全耦合问题的一般数值计算方法。Taron and Elsworth (2009)利用TOUGHREACT模拟热‒流‒化学(THC)耦合过程, 同时叠加 FLAC 3D软件模拟的力学(M)过程, 开发出一种能够再现裂隙岩体不排水加载特性的耦合THMC模拟系统。Poulet et al. (2010)开发了一个用于在统一的多尺度热力学框架内模拟地质应用中THMC过程的数值代码, 其中, 热‒力部分遵循Regenauer-Lieb et al. (2010)的方法, 水文部分遵循多孔介质中的达西渗流假设, 并使用基于吉布斯自由能最小化的HCH软件(Shvarov and Bastrakov, 1999)的组件WinGibbs来处理水岩反应, 化学部分使用PreMDB软件(Siret et al., 2009)来考虑化学反应对材料特性(密度和比热)的影响, 将耦合问题分解为两个子问题, 交互式地进行求解, 直到满足收敛要求。其数值计算结果表明, 所提出的求解方法适用于科学与工程领域中大多数的全耦合问题(Poulet et al., 2010)。

(3) 选取的边界条件和模型参数的问题。施加的边界条件基本上很难跟实际情况一致。目前的研究一般是围绕成矿期流体与各种因素的耦合模拟, 而我们现在能得到的数据大部分都是与现今的地质环境有关的, 而因为矿床后期受到了剥蚀和改造, 很难再获取成矿年代的真实边界条件数据, 所以模型的边界条件只能结合各种已有的地质资料合理地选取。另外, 模型中岩石物性参数选取之后, 大多数都是一个固定值, 而在复杂的地质过程中, 岩石的特性会发生改变, 这些动态变化的参数很难应用于解决问题的模拟当中。比如渗透率的变化, 一旦岩石发生了水力压裂, 流体超压为了加强流体流动从而增大渗透率, 最终使得流体压力下降至低于破裂标准值, 在释放超压后裂隙会关闭, 并且渗透率会回到初始值。然而, 在数值模拟研究中应用了不同的方法, 但是没有一种简单的方法可以实现这种反馈(Weis et al., 2012)。这些存在的问题都是数值模拟在矿床学应用当中需要解决的。

尽管存在着一些还未解决的难题, 但是现阶段计算机数值模拟技术仍可以帮助我们更好地认识成矿动力学机制, 在一定程度上合理地再现复杂地质构造事件的演化过程, 以及推断矿床的时空分布规律, 并可以与地质‒地球物理‒地球化学方面的资料进行联系对比, 从而推动矿床学研究进一步从现象到机理, 从静态到动态, 从定性到定量, 从局部到整体, 同时也为进一步开展找矿预测提供更好的指导。

近年来不断发展的三维成矿预测理论方法, 其理论和实践均已趋向成熟(Yuan et al., 2014; Li et al., 2015; 刘静和陈建平, 2017; 李晓晖等, 2018; 袁峰等, 2018, 2019; 黄松, 2020; Qin et al., 2021; 周永章等, 2021)。国内外的模型模拟研究也已经开始从二维向三维转变, 从单一物理场模拟发展到求解多场耦合问题, 模型边界条件的选取也逐渐从简化往复杂的方向发展, 这意味着所建立的模型将更贴近于真实的地质环境, 使得三维数值模拟方法在真实的三维地质模型和边界条件的约束下能够进行深入的研究(赵义来和刘亮明, 2011; Li et al., 2019), 模拟和预测成矿有利区域, 相关成果可以为深部找矿预测提供新的三维预测信息(袁峰等, 2019)。Li et al. (2019)和胡训宇(2020)将三维数值模拟方法与三维成矿预测方法相结合, 有利于数值模拟方法在矿床学理论研究与成矿预测实践中的发展与应用, 结果表明数值模拟方法能有效提高成矿预测结果的预测能力, 并提供新的深部找矿预测信息。

4 结 语

数值模拟是成矿过程定量化研究的重要手段。数值模拟在热液矿床研究中得到了广泛应用, 为不同矿床的成因提供了有价值的见解, 是其他研究方法的重要补充。对成矿过程中不同影响因素耦合作用的研究, 可查明影响矿床形成的核心因素。在过去四五十年里数值模拟已经取得了巨大进展, 对于热‒流‒力‒化(THMC)全耦合作用的研究仍是数值模拟在矿床学中应用的一块短板, 包括应用三维数值模拟进行成矿预测仍处于初级阶段。因此, 数值模拟研究在矿床学领域的发展仍然具有很大的潜力。

感谢合肥工业大学袁峰教授和中南大学刘亮明教授中肯的修改建议！

陈亮, 陈良波, 唐振平, 胡杨, 刘江, 王正庆, 刘珊, 黄伟, 韩世礼. 2018. 湖南金狮岭地区成矿动力学数值模拟与成矿预测. 南华大学学报(自然科学版), 32(2): 62–69.

戴文强. 2020. 安庆铜矿床热液蚀变及成矿过程数值模拟研究. 合肥: 合肥工业大学硕士学位论文: 41–57.

邓军, 高帮飞, 王庆飞, 杨立强. 2005. 成矿流体系统的形成与演化. 地质科技情报, 24(1): 49–54.

邓军, 孙忠实, 王建平, 杨立强, 王庆飞. 2001. 动力系统转换与金成矿作用. 矿床地质, 20(1): 71–77.

胡训宇. 2020. 南陵‒宣城矿集区成矿过程数值模拟与三维成矿预测. 合肥: 合肥工业大学博士学位论文: 55–94.

黄松. 2020. 山博赛金矿床地质统计学模型构建与三维成矿预测. 北京: 北京科技大学博士学位论文: 93–121.

贾蔡, 袁峰, 张明明, 李晓晖, 周涛发, 邵尉, 郑通科, 高道明. 2014. 宁芜盆地白象山铁矿床成矿作用过程数值模拟. 岩石学报, 30(4): 1031–1040.

贾跃明. 1996. 流体成矿系统与成矿作用研究. 地学前缘, 3(3–4): 94–99.

鞠明辉. 2011. 广西大厂矿田非线性成矿动力耦合过程数值模拟研究. 长沙: 中南大学博士学位论文: 62–108.

李晓晖, 戴文强, 袁峰, 张明明, 胡训宇, 周涛发, 李建设, 陆三明. 2018. 三维成矿预测数据整合过程不确定性研究——以宁芜盆地钟姑矿田为例. 岩石学报, 34(11): 3235–3243.

李增华, 池国祥, 邓腾, 许德如. 2019. 活化断层对加拿大阿萨巴斯卡盆地不整合型铀矿的控制. 大地构造与成矿学, 43(3): 518–527.

刘波, 韩彦辉. 2005. FLAC原理、实例与应用指南. 北京: 人民交通出版社: 1–5.

刘静, 陈建平. 2017. 我国三维成矿预测的研究现状及发展趋势. 地质学刊, 41(3): 441–447.

刘亮明, 疏志明, 赵崇斌, 万昌林, 蔡爱良, 赵义来. 2008. 矽卡岩矿床的汇流扩容空间控矿机制及其对深部找矿的意义: 以铜陵‒安庆地区为例. 岩石学报, 24(8): 1848–1856.

闵令帅, 程惠红, 石耀霖. 2020. 区域岩浆热液成矿的数值模拟——以熊耳山前河地区金矿为例. 中国科学院大学学报, 37(3): 324–335.

任梦依. 2016. 海底多金属硫化物定量预测理论与实践. 北京: 中国地质大学(北京)博士学位论文: 58–160.

王仁. 1994. 有限单元等数值方法在我国地球科学中的应用和发展. 地球物理学报, 37(S1): 128–139.

王勖成, 邵敏. 1988. 有限单元法基本原理与数值方法. 北京: 清华大学出版社: 482–507.

席先武, 杨立强, 王岳军, 邓军, 林舸, 王建平, 雷小青. 2003. 构造体制转换的温度场效应及其耦合成矿动力学数值模拟. 地学前缘, 10(1): 47–55.

徐传福, 车永刚, 李大力, 王勇献, 王正华. 2020. 天河超级计算机上超大规模高精度计算流体力学并行计算研究进展. 计算机工程与科学, 42(10): 1815–1826.

袁峰, 李晓晖, 张明明, 贾蔡, 胡训宇. 2018. 三维成矿预测研究进展. 甘肃地质, 27(1): 32–36.

袁峰, 张明明, 李晓晖, 葛粲, 陆三明, 李建设, 周宇章, 兰学毅. 2019. 成矿预测: 从二维到三维. 岩石学报, 35(12): 3863–3874.

张嵩松. 2011. 岩浆热液成矿系统的数值模拟——以云南个旧锡多金属矿区为例. 北京: 中国地质大学(北京)硕士学位论文: 26–45.

张婉秋, 邹艳红. 2020. 基于TOUGHREACT的成矿过程化学反应数值模拟——以虎头崖铅锌多金属矿床为例. 地质找矿论丛, 35(3): 354–362.

赵鹏大. 2007. 成矿定量预测与深部找矿. 地学前缘, 14(5): 1–10.

赵鹏飞, 王功文, 韩小梦, 牛仲行, 王兵. 2017. 基于FLAC3D成矿过程数值模拟: 以南泥湖钼矿床为例. 中国矿业, 26(S1): 286–290+297.

赵义来, 刘亮明. 2011. 复杂形态岩体接触带成矿耦合动力学三维数值模拟: 以安庆铜矿为例. 大地构造与成矿学, 35(1): 128–136.

周叶. 2007. 挤压应力作用下的构造变形数值模拟研究. 广州: 中国科学院研究生院(广州地球化学研究所)博士学位论文: 45–69.

周永章, 左仁广, 刘刚, 袁峰, 毛先成, 郭艳军, 肖凡, 廖杰, 刘艳鹏. 2021. 数学地球科学跨越发展的十年: 大数据、人工智能算法正在改变地质学. 矿物岩石地球化学通报, 40(3): 556–573+777.

Aavatsmark I. 2002. An introduction to multipoint flux approximations for quadrilateral grids., 6(3–4): 405–432.

Aghbelagh Y B and Yang J. 2014. Effect of graphite zone in the formation of unconformity-related uranium deposits: Insights from reactive mass transport modeling., 144: 12–27.

Ague J J and Brimhall G H. 1989. Geochemical modeling of steady state fluid flow and chemical reaction during supergene enrichment of porphyry copper deposits., 84(3): 506–528.

Andersen C and Weis P. 2020. Heat transfer from convecting magma reservoirs to hydrothermal fluid flow systems constrained by coupled numerical modelling., 47(23): e2020GL089463.

Appold M S and Nunn J A. 2005. Hydrology of the Western Arkoma basin and Ozark platform during the Ouachita orogeny: Implications for Mississippi Valley-type ore formation in the Tri-State Zn-Pb district., 5(4): 308–325.

Bethke C M. 1985. A numerical model of compaction-driven groundwater flow and heat transfer and its application to the paleohydrology of intracratonic sedimentary basins.:, 90(B8): 6817–6828.

Bethke C M. 1986. Hydrologic constraints on the genesis of the Upper Mississippi Valley mineral district from Illinois basin brines., 81(2): 233–249.

Bethke C M, Lee M K and Park J. 2007. Basin Modeling with Basin 2, a Guide to Using the Basin 2 Software Package, Release 5. 0. 1. Hydrogeology Program. University of Illinois.

Bethke C M, Lee M K, Quinodoz H and Kreiling W N. 1993. Basin modeling with Basin2: A guide to using Basin 2, B2plot, B2video, and B2view.University of Illinois Hydrogeology Program: 1–225.

Chi G X. 2001. BsnMod: A WindowsTMprogram for simulating basin-scale fluid flow and heat transfer processes related to sediment compaction and tectonicuplifting in two dimensions. Natural Resources Canada, Geological Survey of Canada: 1–14.

Chi G X, Bosman S and Card C. 2013. Numerical modeling of fluid pressure regime in the Athabasca basin and implications for fluid flow models related to the unconformity-type uranium mineralization., 125: 8–19.

Chi G X, Lavoie D, Bertrand R and Lee M K. 2010. Downward hydrocarbon migration predicted from numericalmodeling of fluid overpressure in the Paleozoic Anticosti Basin, eastern Canada., 10(3): 334–350.

Chi G X, Li Z H and Bethune K. 2014. Numerical modeling of hydrocarbon generation in the Douglas Formation of the Athabasca basin (Canada) and implications for unconformity-related uranium mineralization., 144: 37–48.

Chi G X, Qing H R, Xue C J and Zeng R. 2006. Modeling of fluid pressure evolution related to sediment loading and thrust faulting in the Lanping basin: Implications for the formation of the Jinding Zn-Pb deposit, Yunnan, China., 89(1–3): 57–60.

Chi G X and Savard M M. 1998. Basinal fluid flow models related to Zn-Pb mineralization in the southern margin of the Maritimes Basin, eastern Canada., 93: 896–910.

Chi G X and Xue C J. 2011. An overview of hydrodynamic studies of mineralization., 2(3): 423–438.

Cline J S, Bodnar R J and Rimstidt J D. 1992. Numerical simulation of fluid flow and silica transport and deposition in boiling hydrothermal solutions: Application to epithermal gold deposits.:, 97(B6): 9085–9103.

Cooke D R and McPhail D C. 2001. Epithermal Au-Ag-Te mineralization, Acupan, Baguio district, Philippines: Numerical simulations of mineral deposition., 96(1): 109–131.

Cox S F. 2005. Coupling between deformation, fluid pressures, and fluid flow in ore-producing hydrothermal systems at depth in the crust., 100: 39–75.

Cui T, Yang J W and Samson I M. 2010. Numerical modelingof hydrothermal fluid flow in the Paleoproterozoic Thelon Basin, Nunavut, Canada., 106(1–3): 69–76.

Cui T, Yang J W and Samson I M. 2012. Tectonic deformation and fluid flow: Implications for the formation of unconformity-related uranium deposits.,107(1): 147–163.

Diersch H J G. 2002. FEFLOW Finite Element Subsurface Flow and Transport Simulation System: User’s Manual/ Reference Manual/White Papers. WASY Ltd, Berlin Release: 5.

Diersch H J G and Kolditz O. 1998. Coupled groundwater flow and transport: 2. Thermohaline and 3D convection systems., 21(5): 401–425.

Driesner T and Geiger S. 2007. Numerical simulation of multiphase fluid flow in hydrothermal systems., 65(1): 187–212.

Driesner T, Weis P and Scott S. 2015. A new generation of numerical simulation tools for studying the hydrology of geothermal systems to “supercritical” and magmatic conditions. World Geothermal Congress: 1–4.

Elder J W. 1967. Steady free convection in a porous medium heated from below., 27(1): 29–48.

Eldursi K, Branquet Y, Guillou-Frottier L and Marcoux E. 2009. Numerical investigation of transient hydro­thermal processes around intrusions: Heat-transfer and fluid-circulation controlled mineralization patterns., 288(1–2): 70–83.

Emmanuel S and Berkowitz B. 2006. An experimental analogue for convection and phase separation in hydrothermal systems.:, 111(B9).

Emmanuel S and Berkowitz B. 2007. Phase separation and convection in heterogeneous porous media: Implicationsfor seafloor hydrothermal systems.:, 112(B5).

Garven G and Freeze R A. 1984. Theoretical analysis of the role of groundwater flow in the genesis of stratabound ore deposits: 1, Mathematical and numerical model., 284(10): 1085–1124.

Geiger S, Haggerty R, Dilles J H, Reed M H and Matthai S K. 2002. New insights from reactive solute transport modeling: The formation of sericitic vein envelopes during early hydrothermal alteration at Butte, Montana., 2: 185–201.

Griebel M, Dornseifer T and Neunhoeffer T. 1998. Numerical simulation in fluid dynamics: A practical introduction. Society for Industrial and Applied Mathematics: 1–17.

Harbaugh A W. 2005. MODFLOW-2005, The U. G. Geological Survey Modular Groundwater Model: The Groundwater Flow Process. U. S. G. S. Techniques and Methods 6–A16: 253.

Hobbs B E, Means W D and Williams P F. 1976. An outline of structural geology. New York, Wiley: 571.

Hobbs B E, Zhang Y, Ord A and Zhao C. 2000. Application of coupled deformation, fluid flow, thermal and chemical modelling to predictive mineral exploration., 69: 505–509.

Hu X Y, Li X H, Yuan F, Ord A, Jowitt S M, Li Y, Dai W Q and Zhou T F. 2020. Numerical modeling of ore-formingprocesses within the Chating Cu-Au porphyry-type deposit, China: Implications for the longevity of hydrothermal systems and potential uses in mineral exploration., 116: 103230.

Ingebritsen S E and Appold M S. 2012. The Physical Hydrogeology of Ore Deposits., 107(4): 559–584.

Ingebritsen S E, Geiger S, Hurwitz S and Driesner T. 2010. Numerical simulation of magmatic hydrothermal systems., 48(1).

Itasca. 2002. PFC2D, Particle Flow Code in 2 Dimensions. User Manual, Version 3.0. Itasca Consulting Group, Inc., Minneapolis.

Jaeger J C and Cook N G W. 1979. Fundamentals of rock mechanics. Chapman and Hall, London: 593.

Jing L R and Feng X T. 2003. Numerical Modeling for Coupled Thermal-Hydro-Mechanical and Chemical Processes (THMC) of Geological Media—International and Chinese Experiences., (10): 1704–1715.

Joshua T, Derek E and Min K B. 2009. Numerical simulation of thermal-hydrologic-mechanical-chemical processes in deformable, fractured porous media., 46(5): 842–854.

Ju M H, Zhao C, Dai T G and Yang J W. 2011. Finite element modeling of pore-fluid flow in the Dachang ore district, Guangxi, China: Implications for hydrothermal mineralization., 2(3): 463–474.

Kipp K L, Hsieh P A and Charlton S R. 2008. Guide to the Revised Ground-Water Flow and Heat Transport Simulator: HYDROTHERM-Version 3. US Department of the Interior, US Geological Survey.

Leach D L and Sangster D F. 1993. Mississippi Valley-type lead-zinc deposits., 40(3): 108–117.

Lee S H, Jenny P and Tchelepi H A. 2002. A finite-volume method with hexahedral multiblock grids for modeling flow in porous media., 6(3–4): 353–379.

Lewis K C. 2007. Numerical modeling of two-phase flow in the sodium chloride-water system with applications to seafloor hydrothermal systems. Georgia Institute of Technology: 1–178.

Li X H, Yuan F, Zhang M M, Jia C, Jowitt S M, Ord A, Zheng T K, Hu X Y and Li Y. 2015. Three-dimensional mineral prospectivity modeling for targeting of concealedmineralization within the Zhonggu iron orefield, Ningwu Basin, China., 71: 633–654.

Li X H, Yuan F, Zhang M M, Jowitt S M, Ord A, Zhou T F and Dai W Q. 2019. 3D computational simulation- based mineral prospectivity modeling for exploration for concealed Fe-Cu skarn-type mineralization within the Yueshan orefield, Anqing district, Anhui Province, China., 105: 1–17.

Li Z H, Chi G X and Bethune K M. 2016. The effects of basement faults on thermal convection and implications for the formation of unconformity-related uranium deposits in the Athabasca Basin, Canada., 16: 729–751.

Li Z H, Chi G X, Bethune K M, Eldursi K, Quirt D, Ledru P and Gudmundson G. 2018a. Numerical simulation of strain localization and its relationship to formation of the Sue unconformity-related uranium deposits, eastern Athabasca Basin, Canada., 101(July): 17–31.

Li Z H, Chi G X, Bethune K M, Eldursi K, Quirt D, Ledru P and Thomas D. 2020. Interplay between thermal convection and compressional fault reactivation in the formation of unconformity-related uranium deposits.: 1–16. https: //doi.org/10.1007/s00126-020- 01011-6.

Li Z H, Chi G X, Bethune K M, Eldursi K, Thomas D, Quirt D and Ledru P. 2018b. Synchronous egress and ingress fluid flow related to compressional reactivation of basement faults: The Phoenix and Gryphon uranium deposits, southeastern Athabasca Basin, Saskatchewan, Canada., 53(2): 277–292.

Li Z H, Chi G X, Bethune K M, Thomas D and Zaluski G. 2017. Structural controls on fluid flow during compressionalreactivation of basement faults: Insights from numerical modeling for the formation of unconformity-related uranium deposits in the athabasca Basin, Canada., 112(2): 451–466.

Lin G, Zhou Y, Wei X R and Zhao C B. 2006. Structural controls on fluid flow and related mineralization in the Xiangshan uranium deposit, Southern China., 89(1–3): 231–234.

Liu L M, Li J F, Zhou R C and Sun T. 2016. 3D modeling of the porphyry-related Dawangding gold deposit in south China: Implications for ore genesis and resources evaluation., 164: 164–185.

Liu L M, Wan C L, Zhao C B and Zhao Y L. 2011. Geodynamicconstraints on orebody localization in the Anqing orefield, China: Computational modeling and facilitating predictive exploration of deep deposits., 43(1): 249–263.

Liu L M, Yang G Y, Peng S L and Zhao C. 2005. Numerical modeling of coupled geodynamical processes and its role in facilitating predictive ore discovery: An example from Tongling, China., 55(1): 21–31.

Liu L M, Zhao Y L and Sun T. 2012. 3D computational shape- and cooling process-modeling of magmatic intrusion and its implication for genesis and exploration of intrusion-related ore deposits: An example from the Yueshan intrusion in Anqing, China., 526: 110–123.

Liu L M, Zhao Y L and Zhao C B. 2010. Coupled geodynamics in the formation of Cu skarn deposits in the Tongling- Anqing district, China: Computational modeling and implications for exploration., 106(1–3): 146–155.

Liu Y and Dai T G. 2014. Numerical modeling of pore-fluid flow and heat transfer in the Fushan iron ore district, Hebei, China: Implications for hydrothermal mineralization., 144: 115–127.

Mandl G. 1988. Mechanics of tectonic faulting. Amsterdam, Elsevier: 704.

Mannington W, O’ Sullivan M and Bullivant D. 2004. Computer modeling of the Wairakei-Tauhara geothermal system, New Zealand., 33: 401–419.

McDonald M G and Harbaugh A W. 1984. A modular three-dimensional finite-difference groundwater flow model (Open-file report 83-875). US Department of the Interior. US Geological Survey, Reston, VA: 528.

McLellan J G, Oliver N H S and Schaubs P M. 2004. Fluid flow in extensional environments; numerical modelling with an application to Hamersley iron ores., 26(6–7): 1157–1171.

Menand T, Raw A and Woods A W. 2003. Thermal inertia and reversing buoyancy in flow in porous media., 30(6): 24.

Misra K C. 2000. Skarn deposits // Understanding mineral deposits. Springer, Dordrecht: 414–449.

Narasimhan T N and Witherspoon P A. 1976. An integrated finite difference method for analyzing fluid flow in porous media., 12(1): 57–64.

Oliver N H, McLellan J G, Hobbs B E, Cleverly J S, Ord A and Feltrin L. 2006. Numerical models of extensional deformation, heat transfer, and fluid flow across basement- cover interfaces during basin-related mineralization., 101(1): 1–31.

Ord A. 1991. Deformation of rock: A pressure-sensitive, dilatant material., 137(4): 337–366.

Ord A and Oliver N H S. 1997. Mechanical controls on fluid flow during regional metamorphism: Some numerical models., 15(3): 345–359.

Poulet T, Karrech A, Regenaur-Lieb K, Gross L, Cleverley J S and Georgiev D. 2010. Thermal-mechanical-hydrological-chemical simulations using escript, Abaqus and WinGibbs // Abstract for the GeoMod 2010 Conference, 27e29 September.

Pruess K. 1991. TOUGH2: A General-Purpose numerical Simulator for Multiphase Fluid and Heat Flow. Report LBL-20700, Berkeley, California: Lawrence Berkeley Laboratory.

Qin Y Z, Liu L M and Wu W C. 2021. Machine Learning- Based 3D Modeling of Mineral Prospectivity Mapping in the Anqing Orefield, Eastern China.: 1–22. https: //doi.org/10.1007/s11053-021- 09893-7.

Regenauer-Lieb K, Karrech A, Chua H T, Horowitz F G and Yuen D. 2010. Time-dependent, irreversible entropy production and geodynamics.:,, 368(1910): 285–300.

Sanford R F. 1994. A quantitative model of groundwater flow during formation of tabular sandstone uranium deposit., 89: 341–360.

Schaubs P M, Rawling T J, Dugdale L J and Wilson C J L. 2006. Factors controlling the location of gold mineralisation around basalt domes in the Stawell corridor: Insights from coupled 3D deformation-fluid-flow numerical models., 53(5): 841–862.

Scott S, Driesner T and Weis P. 2015. Geologic controls on supercritical geothermal resources above magmatic intrusions., 6(1): 1–6.

Scott S, Driesner T and Weis P. 2016. The thermal structure and temporal evolution of high-enthalpy geothermal systems., 62: 33–47.

Scott S, Driesner T and Weis P. 2017. Boiling and condensation of saline geothermal fluids above magmatic intrusions., 44(4): 1696–1705.

Sharp J M. 1978. Energy and momentum transport model of the Ouachita basin and its possible impact on formation of economic mineral deposits., 73(6): 1057–1068.

Shvarov Y V and Bastrakov E. 1999. HCh: A software package for geochemical equilibrium modeling // User’s guide. Australian Geological Survey Organisation, Department of Industry. Science and Resources.

Sillitoe R H. 2010. Porphyry copper systems., 105(1): 3–41.

Siret D, Poulet T, Regenauer-Lieb K and Connolly J A D. 2009. PreMDB, a thermodynamically consistent material database as a key to geodynamic modelling., 4(2): 107–115.

Sondergeld C H and Turcotte D L. 1977. An experimental study of two-phase convection in a porous medium with applications to geological problems., 82(14): 2045–2053.

Sorjonen-Ward P, Zhang Y and Zhao C. 2002. Numerical modelling of orogenic processes and gold mineralisation in the southeastern part of the Yilgarn Craton, Western Australia., 49(6): 935–964.

Takahashi H, Tomita S A, Koike K and Yoshiyama H. 2020. A cold-water trap as an essential process for the generation of low-sulfidation epithermal deposits: Geological and numerical studies of the Hosokura deposit, northern Japan., 128: 103780.

Taron J and Elsworth D. 2009. Thermal-hydrologic-mechanical- chemical processes in the evolution of engineered geothermal reservoirs., 46(5): 855–864.

Taron J, Elsworth D and Min K B. 2009. Numerical simulation of thermal-hydrologic-mechanical-chemical processes in deformable, fractured porous media., 46(5): 842–854.

Todesco M, Chiodini G and Macedonio G. 2003. Monitoring and modeling hydrothermal fluid emission at La Solfatara (Phlegrean Fields, Italy): An interdisciplinary approach to the study of diffuse degassing., 125: 57–79.

Vermeer P A and DeBorst R. 1984. Non-associated plasticity for soils, concrete and rock., 29(3): 1–64.

Vigneresse J L. 2019. Addressing ore formation and exploration., 10(4): 1613–1622.

Vigneresse J L and Truche L. 2020. Modeling ore generation in a magmatic context., 116: 103223.

Vigneresse J L, Truche L and Richard A. 2019. How do metals escape from magmas to form porphyry-type ore deposits?, 105: 310–336.

Weis P. 2014. The physical hydrology of ore-forming magmatic-hydrothermal systems // Building Exploration Capability for the 21st Century. Society of Economic Geologists, 18: 59–75.

Weis P, Driesner T and Heinrich C A. 2012. Porphyry- copper ore shells form at stable pressure-temperature fronts with dynamic fluid plumes., 338: 1613– 1616.

Xu T F, Sonnenthal E, Spycher N and Pruess K. 2004. TOUGHREACT user’s guide: A simulation program for non-isothermal multiphase reactive geochemical transportin variable saturated geologic media (No. LBNL-55460). Lawrence Berkeley National Lab. (LBNL), Berkeley, CA (United States): 1‒206.

Xu T F, Sonnenthal E, Spycher N and Pruess K. 2006. TOUGHREACT—A simulation program for non-isothermal multiphase reactive geochemical transport in variably saturated geologic media: Applications to geothermal injectivity and CO2geological sequestration., 32(2): 145–165.

Xue C J, Chi G X and Xue W. 2010. Interaction of two fluid systems in the formation of sandstone-hosted uranium deposits in the Ordos Basin: Geochemical evidence and hydrodynamic modeling., 106: 226–235.

Xue C J, Chi G X and Xue W. 2011. Effects of hydrocarbon generation on fluid flow in the Ordos Basin and relationship with uranium mineralization., 2(3): 439–448.

Yang J, Bull S and Large R. 2004. Numerical investigation of salinity in controlling ore-forming fluid transport in sedimentary basins: Example of the HYC deposit, Nor­thern Australia., 39(5–6): 622–631.

Yapparova A, Miron G D, Kulik D A, Kosakowski G and Driesne T. 2019. An advanced reactive transport simulation scheme for hydrothermal systems modelling., 78: 138‒153.

Yuan F, Li X H, Zhang M M, Jowitt S M, Jia C, Zheng T K and Zhou T F. 2014. Three-dimensional weights of evidence-based prospectivity modeling: A case study of the Baixiangshan mining area, Ningwu Basin, Middle and Lower Yangtze Metallogenic Belt, China., 145: 82–97.

Zhang Y H, Robinson J and Schaubs P M. 2011. Numerical modeling of structural controls on fluid flow and mineralization., 2(3): 449–462.

Zhang Y H, Sorjonen-Ward P, Ord A and Southgate P N. 2006. Fluid flow during deformation associated with structural closure of the Isa superbasin at 1575 Ma in the central and northern Lawn Hill platform, northern Australia., 101(6): 1293–1312.

Zhao C B, Hobbs B E and Mühlhaus H B. 1998. Finite element modelling of temperature gradient driven rock alteration and mineralization in porous rock masses., 165(1–4): 175–187.

Zhao C B, Hobbs B E, Mühlhaus H B, Ord A and Lin G. 2000. Numerical modelling of double diffusion driven reactive flow transport in deformable fluid-saturated porous media with particular consideration of temperature-dependent chemical reaction rates., 17: 367–385.

Zhao C B, Hobbs B E and Ord A. 2018. Modeling of mountain topography effects on hydrothermal Pb-Zn mineralization patterns: Generic model approach., 190: 400–410.

Zhao C B, Hobbs B E, Ord A, Kühn M, Mühlhaus H B and Peng S L. 2006. Numerical simulation of double- diffusion driven convective flow and rock alteration in three-dimensional fluid-saturated geological fault zones., 195(19–22): 2816–2840.

Zou Y H, Yao L, Yong P, Yang K D, Dai T G, Mao X C, Lai J Q and Tian H L. 2019. Numerical simulation of hydrothermal mineralization associated with simplified chemical reactions in Kaerqueka polymetallic deposit, Qinghai, China., 29(1): 165–177.

Application and Prospect of Numerical Simulation of Dynamics on Coupled Multi-processes in Hydrothermal Deposit Research

HUANG Qinyi1, 2, LI Zenghua3, 4*, Xu Deru1, 4, CHI Guoxiang5, DENG Teng4, ZHAO Zhaoxia1, 2and YU Deshui1, 2

(1.510640,; 2.100049,; 3.330013,; 4.330013,; 5.)

Formation of hydrothermal deposit is a complex multi-coupled process, which involves heat transfer, fluid flow and solute transport. With the development of computer technology and computational mathematics, numerical simulation of dynamics on coupled multi-processes has been applied more and more widely in researches of mineralization in recent years, mainly simulating the thermal (T), hydraulic (H), mechanical (M) and chemical (C) processes in the mineralization system as well as their interactions. In this paper, we review the application of numerical simulation methods in the study of ore deposits, including (1) a brief introduction of general theories and the commonly used numerical simulation software; (2) the application of numerical simulation of dynamics on coupled multi-processes in the studies of the Mississippi Valley-type Pb-Zn, unconformity-related uranium, porphyry, skarn deposits and the metallogenetic prediction; and (3) a discussion of the significance and limitations of numerical simulation for the study of metallogenic processes and its future directions. Numerical simulation is an effective analytical tool to solve some complicated geological problems, which will promote the transformation of ore deposit research from qualitative and semi-quantitative to quantitative.

numerical simulation; numerical simulation software; mineralization; coupled dynamics

P611, P628+.3

A

1001-1552(2021)06-1146-015

10.16539/j.ddgzyckx.2021.06.002

2020-06-23;

2021-07-08

国家自然科学基金(41930428、42002090)和东华理工大学江西省放射性地学大数据技术工程实验室开放基金(JELRGBDT202006)联合资助。

黄沁怡(1996–), 女, 博士研究生, 主要从事成矿构造与矿产预测的数值模拟研究。Email: huangqinyi@gig.ac.cn

李增华(1983–), 男, 教授, 从事成矿流体动力学研究。Email: lizenghua@ecut.edu.cn