The Depth Distribution of Constacyclic Codes Over the Ring Fp+vFp+v2Fp
2022-01-11
Abstract:In this paper,we studied the depth spectrum and the depth distribution of constacyclic codes over the non-chain ring R=Fp+vFp+v2Fp,where v3=v.By decomposing the linear codes C over R into the linear codes over the finite field Fp,three corresponding constacyclic codes C1,C2,C3 over Fp were obtained.Furthermore,considering the depth spectrum of constacyclic codes over the finite filed Fp,and the relationship between constacyclic codes C1,C2,C3 and C,the depth spectrum and the depth distribution of constacyclic codes over R were discussed.
Keywords:Constacyclic code;Depth spectrum;Depth distribution;Non-chain ring
§1.Introduction
The depth distribution was first introduced by Etzion [1] as an important characterization of linear codes.Soon afterwards,Mitchell [7] studied the depth spectrum and depth distribution for the cyclic codes over finite fields.Luoet al.[6] obtained a number of properties about the depth distribution of linear codes over Fpand determined the depth distribution of Reed-Muller codes.Deng [2] studied the properties of the binary linear codesCand their depth spectrums.
In recent years,there have been many related researches on depth spectrum and depth distribution of linear codes over finite rings.For example,the depth spectrum of cyclic codes over Z4of odd length was introduced by Zhuet al[12].Soon,Kaiet al[4] determined the depth spectrum of negacyclic codes over Z4of even length.The depth spectrum of simple-root constacyclic codes over a finite chain ring was discussed by Konget al[5].Yaoet al[9] obtained the depth spectrums and depth distribution of linear codes over F2+uF2+u2F2withu3=1.Wood [8] showed that finite Frobenius rings are suitable for coding alphabets,which leads to many works on non-chain rings.For instance,Zhang studied self-dual codes over the non-chain ring Fp+vFpwithv2=vin [11],later,the depth distrubution of constacyclic codes over that ring was studied in [10].
Motivated by those work mentioned above,we extend the ring further toR=Fp+vFp+v2Fpwithv3=v,which is a non-chain ring.We will determine the depth spectrum and depth distribution of constacyclic codes over the ringR.The rest of this paper is arranged as follows.In Section 2,we introduce some necessary notation and recall some preliminaries.In Section 3,the depth spectrum of linear codes overRare studied.In Section 4,we first determine the depth spectrum of constacyclic codes overR,and then we give the depth distribution of constacyclic codes.Section 5 is the conclusion of the paper.
§2.Preliminaries
Let Fpbe a finite field withpelements,wherepis an odd prime,and letRbe the finite ring Fp+vFp+v2Fpwithv3=v,which is a finite communicative ring with identity.The derivative operationDoverRnis defined to be
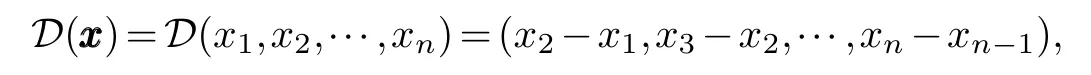
for∀xxx=(x1,x2,···,xn)∈Rn.If there is a smallest positive integerisuch thatDi(xxx)=(0n−i),whereDi(xxx) representsiderivative operations on vectorxxxand (0m) stands for the all-0 vector of lengthm,then the integeriis referred to as thedepthofxxxand denoted bydepth(xxx),i.e.,depth(xxx)=i.If no suchiexists,then the depth ofxxxis defined to ben.
For a linear codeCoverR,we denote byDi(C) the number of codewords inCof depthi.The numbersD0(C),D1(C),···,Dn(C) are referred to as thedepth distributionofC.ObviouslyD0(xxx)=1.Further,thedepth spectrumofC,denoted byDepth(C),is defined asDepth(C)={i|1≤i≤n,Di(C)/=0}.Let|Depth(C)|be the number of elements ofDepth(C).
A linear codeCof lengthnover the finite field Fpis calledλ−constacyclicif(c0,c1,···,cn−1)∈Cimplies that (λcn−1,c0,···,cn−2)∈C.In particular,1-constacyclic codes are calledcyclic codes.It is known that eachλ-constacyclic code of lengthnover Fpis regarded as an ideal of Fp[x]/〈xn −λ〉.Thus anyλ-constacyclic codeCis generated byg(x)+〈xn −λ〉,whereg(x)∈Fp(x)is a unique minor factor polynomial ofxn −λ.The polynomialg(x)is referred to as thegenerator polynomialof theλ-constacyclic codesCover Fp.
We define the Gray map as in [3]:
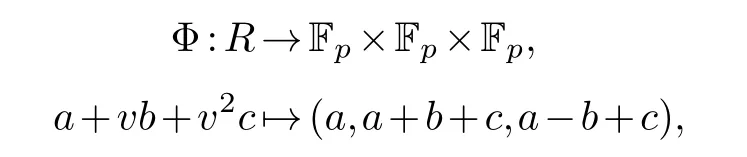
wherea,b,c∈Fp.Note that every elementαinRnhas the following expression:
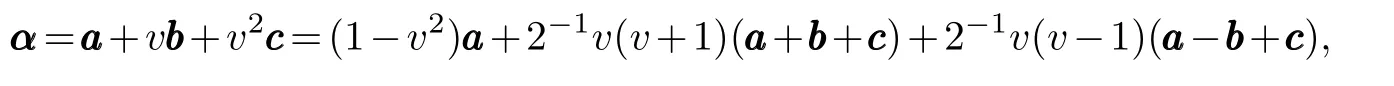
whereDefineC1,C2andC3as follows:
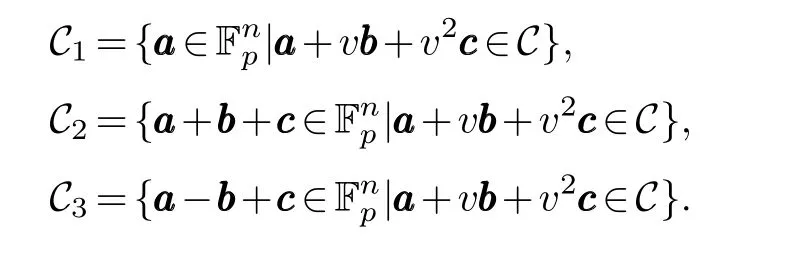
ThenC1,C2andC3are obviously linear over Fp.
By virtue of the Gray map Φ we know that any linear code of lengthnover Fp+vFp+v2Fphas the following unique direct decomposition.
Theorem 2.1.[3] Let C be a linear code of length n over R.Then C can be uniquely expressed as
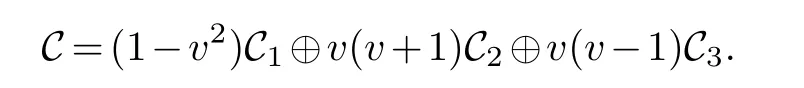
§3.Depth spectrum of linear codes over R
In this section,we first recall two results on depth and depth spectrum of constacyclic codes over Fpin the following lemmas,respectively,and then characterize the spectrum of linear codes overR.
Lemma 3.1.[6]Let C be an[n,k]linear codes overFp.Then for all nonzero codewords of C,there are exactly k distinct depths d1 Lemma 3.2.[10] Let α be a nonzero element ofFp satisfying α/=1.Suppose that C is an[n,k]α-constacyclic code overFp.Then the depth spectrum of C is {n,n−1,···,n−k+1}. LetC=(1−v2)C1⊕v(v+1)C2⊕v(v−1)C3be a linear code of lengthnoverRwith generator matrixG.LetG1,G2andG3be generator matrices ofC1,C2andC3,and let their dimensions arek1,k2andk3,respectively.Assume that the depth spectrums ofC1,C2andC3are{r1,r2,···,rk1},{s1,s2,···,sk2}and{t1,t2,···,tk3},respectively,wherer1 Theorem 3.1.With the above notation,let C be a linear code of length n over R.Then andmax{k1,k2,k3}≤|Depth(C)|≤k1+k2+k3. Proof.Note thatCcan be uniquely expressed asC=(1−v2)C1⊕v(v+1)C2⊕v(v−1)C3.Therefore,it suffices to compute the depth spectrum of (1−v2)C1⊕v(v+1)C2⊕v(v−1)C3.Letccc1,ccc2andccc3be three nonzero codewords satisfyingccc1∈C1,ccc2∈C2andccc3∈C3.Writecccas(1−v2)ccc1+v(v+1)ccc2+v(v−1)ccc3.Hence Thereforedepth(ccc)∈{max{ri,sj,tl}|1≤i≤k1,1≤j ≤k2,1≤l ≤k3}. In addition,since (1−v2)C1,v(v+1)C2andv(v−1)C3are three subcodes ofC,we immediately get thatDepth((1−v2)C1)⊆Depth(C),Depth(v(v+1)C2)⊆Depth(C) andDepth(v(v−1)C3)⊆Depth(C).Thus from the fact thatDepth((1−v2)C1)=Depth(C1),Depth(v(v+1)C2)=Depth(C2) andDepth(v(v−1)C3)=Depth(C3) we obtain It is obvious that max{k1,k2,k3}≤|Depth(C)|≤k1+k2+k3. Letλ=χ+vψ+v2ω,whereχ,ψ,ω ∈Fp.We can now establish: Lemma 4.1.A linear code of length n over R can be represented as C=(1−v2)C1⊕v(v+1)C2⊕v(v−1)C3.Then C is λ-constacyclic if and only if C1is χ-constacyclic,C2is(χ+ψ+ω)-constacyclic over and C3is(χ−ψ+ω)-constacyclic overFp,respectively. Proof.Suppose thatCisλ-constacyclic.Let Writexi=(1−v2)ai+v(v+1)bi+v(v−1)ci,0≤i≤n−1.Then Therefore, It follows that (λcn−1,c0,···,cn−2)∈Cfrom the fact thatCisλ-constacyclic.This yields that which shows that (χan−1,a0,···,an−2)∈C1,((χ+ψ+ω)bn−1,b0,···,bn−2)∈C2and ((χ−ψ+ω)cn−1,c0,···,cn−2)∈C3.ThereforeC1isχ-constacyclic,C2is (χ+ψ+ω)-constacyclic andC3is(χ−ψ+ω)-constacyclic. Conversely,let (x0,x1,···,xn−1)∈C,wherexi=(1−v2)ui+v(v+1)zi+v(v−1)wi,0≤i≤n−1.That is to say,(1−v2)(u0,u1···un−1)+v(v+1)(z0,z1,···zn−1)+v(v−1)(w0,w1,···,wn−1)=(x0,x1,···,xn−1)∈C,which implies that SinceC1isχ-constacyclic,C2is (χ+ψ+ω)-constacyclic andC3is (χ−ψ+ω)-constacyclic codes,we have that ThusCisλ-constacyclic. Corollary 4.1.Let C=(1−v2)C1⊕v(v+1)C2⊕v(v−1)C3be a linear code of length n over R.Then C is a cyclic code of length n over R if and only if all of C1,C2and C3are cyclic codes of length n overFp. LetC=(1−v2)C1⊕v(v+1)C2⊕v(v−1)C3be aλ-constacyclic code of lengthnoverR,we have the following depth spectrum theorem. Theorem 4.1.Let λ=χ+vψ+v2ω be a unit of R with χ/=1,χ+ψ+ω/=1and χ−ψ+ω/=1.Then Proof.From Lemma 4.1,we know thatC1is [n,k1]χ-constacyclic code,C2is [n,k2](χ+ψ+ω)-constacyclic code andC3is [n,k3] (χ−ψ+ω)-constacyclic code over Fp,respectively.Then the depth spectrums ofCi(i=1,2,3) are{n,n−1,···,n−ki+1}(i=1,2,3).According to Theorem 3.1,we obtain depth spectrum ofC. IfCi(i=1,2,3) is a cyclic code,then we suppose that (x−1)λi‖(xn −1)/gi(x) (i=1,2,3),where“‖”denotes“exactly divides”,i.e.,a(x)r‖b(x) means thata(x)r|b(x) anda(x)r+1łb(x). Lemma 4.2.[9]Suppose that C is an[n,k]cyclic code overFp which has the generator polynomial g(x).Let deg(g(x))=n−k and(x−1)ξ‖(xn −1)/g(x).Then Theorem 4.2.Let λ=χ+vψ+v2ω be a unit of R with χ=1,χ+ψ+ω=1and χ−ψ+ω=1.Then Proof.It’s easy to know from the conditions thatC1,C2andC3are cyclic codes of lengthnover Fp.From Lemma 4.2 and Theorem 3.1,we obtain depth spectrum ofC. Similar to Theorems 4.1 and 4.2,we can obtain the depth spectrum in all cases.Letλ=χ+vψ+v2ωbe a unit ofR.We write out the depth spectrum in Table 1. Table 1 Depth spectrum of C. According to Table 1,we compare it with the depth spectrum of constacyclic codes in [10].The methods of discussing the classification of constacyclic codeCover finite field are similar.But it is different from the ring in [10] in that the non-chain ring is further expanded to Fp+vFp+v2Fpwithv3=v.Ifv2=v,it can degenerate to the result of [10]. Theorem 4.3.With the notation as in Case 1 in Table 1.Suppose that k1≥k2≥k3.Then the depth distribution of C is given by Proof.If 1≤i≤k1-k2,then Ifk1-k2+1≤i≤k1-k3,then Ifk1-k3+1≤i≤k1,then Thus,we complete the proof. Remark 4.1.Here we give the depth distribution when k1≥k2≥k3,and other ordering situations of k1,k2and k3are similar and omitted. With the notation as in Case 2 in Table 1.Suppose thatλ1=max{λ1,λ2,λ3}.Denote For convenience,we will only study the depth distribution ofCforλ1≥λ2≥λ3andk1−λ1≥k2−λ2≥k3−λ3.Other situations are similar and neglected. Theorem 4.4.With the notation as in Case 2 in Table 1.Suppose that λ1≥λ2≥λ3,and let k1−λ1≥k2−λ2≥k3−λ3.Then the depth distribution of C is given by Proof.We have five cases: (1) 1≤i≤λ3, (2)λ3+1≤i≤λ2, (3)λ2+1≤i≤k1−k2+λ2, (4)k1−k2+λ2+1≤i≤k1−k3+λ3, (5)k1−k3+λ3+1≤i≤k1, Thus,we complete the proof. With the notation as in Case 3 in Table 1,we denote Then we have For convenience,we only study the depth distribution corresponding to the depth spectrum{d1,···,dk3},and other cases can be discussed similarly and are omitted. Theorem 4.5.With the notation as in Case 3 in Table 1.Suppose k1≤k2≤k3−λ3,then the depth distribution of C is given by Proof.Ifk1≤k2≤k3−λ3,then we have the following three cases: (1) 1≤i≤k3-k2, (2)k3-k2+1≤i≤k3-k1, (3)k3-k1+1≤i≤k3, Thus,we complete the proof. Remark 4.2.The depth distribution corresponding to the depth spectrum in Cases 4 and 5 can be obtained by using the similar method as that in Theorem 4.5.The result can be obtained only by making corresponding substitution. With the notation as in Case 6 in Table 1.Assumeλ1=max{λ1,λ2,λ3}and denote Then we have Again for convenience,only the depth distribution corresponding to the depth spectrum{d1,···,dk1}is discussed here. Theorem 4.6.With the notation as in Case 6 in Table 1.Suppose λ2≤λ1and k3≤k2−λ2≤k1−λ1,then the depth distribution of C is given by Proof.We have four cases: (1) 1≤i≤λ2, (2)λ2+1≤i≤k1-k2+λ2, (3)k1-k2+λ2+1≤i≤k1-k3, (4)k1-k3+1≤i≤k1. Thus,we complete the proof. Remark 4.3.Similarly,the depth distribution corresponding to the depth spectrum in Cases 7 and 8 in Table 1 can be obtained by using the same method as that in Theorem 4.6. In this paper,we determine the depth spectrum and the depth distribution of constacyclic codes over the ringR=Fp+vFp+v2Fp.The depth spectrum of constacyclic codes over the finite field Fpand the direct decomposition in Theoreom 2.1 are used to obtain the depth spectrum of constacyclic codes overR.For the further work,we will consider the constacyclic codes with multiple roots and quasicyclic codes over the ringR.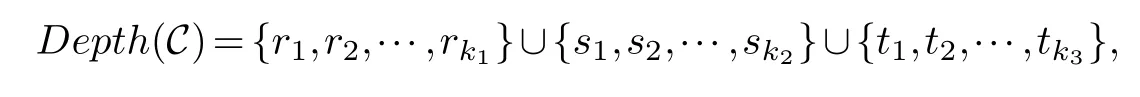
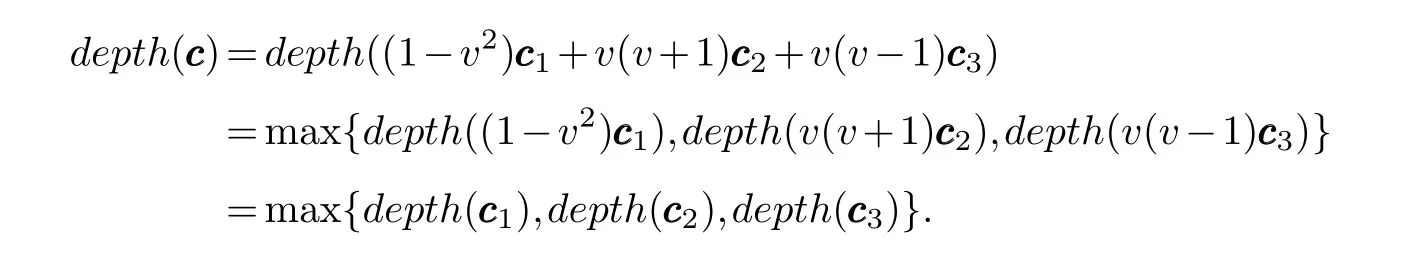
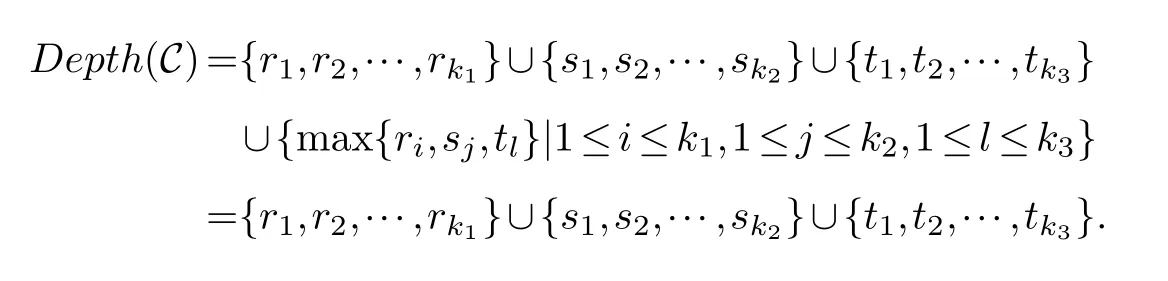
§4.Depth spectrum and depth distribution of constacyclic codes over R
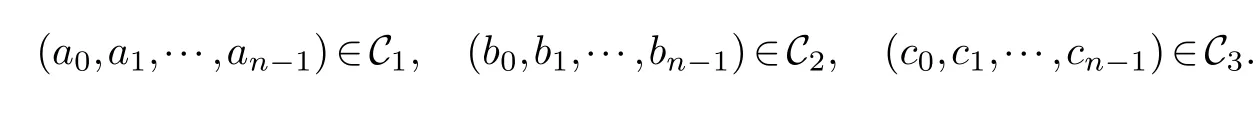
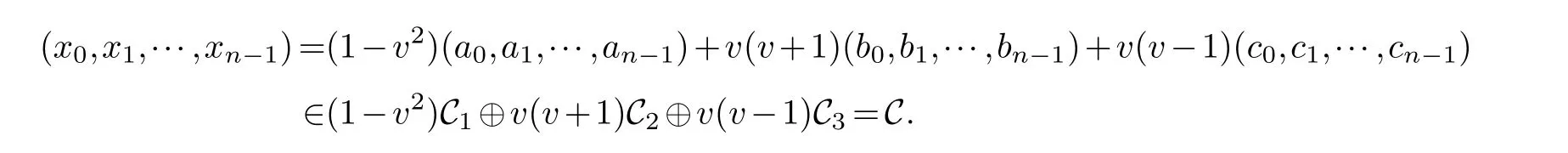
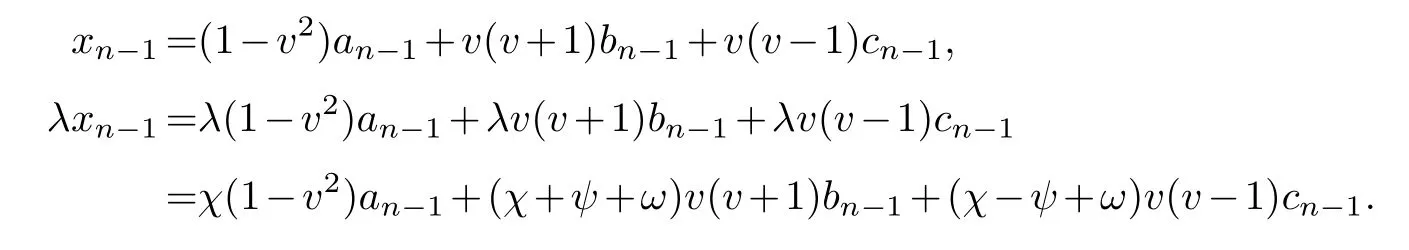


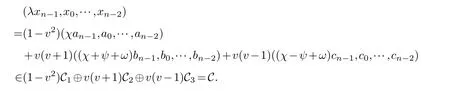
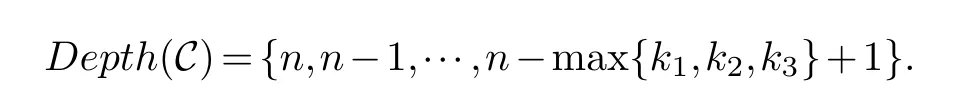
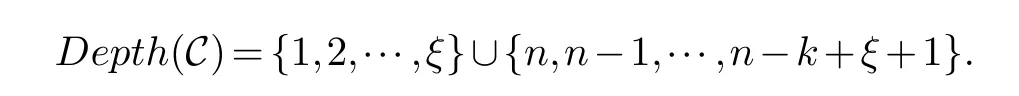
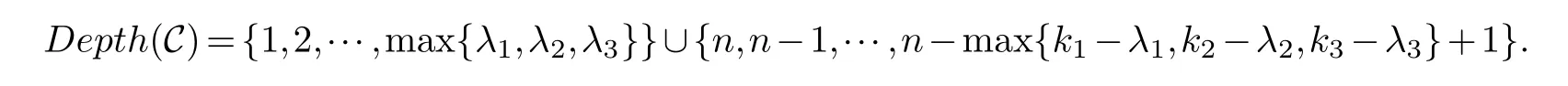


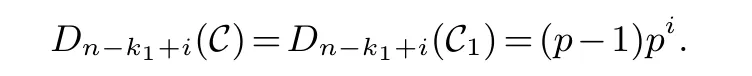
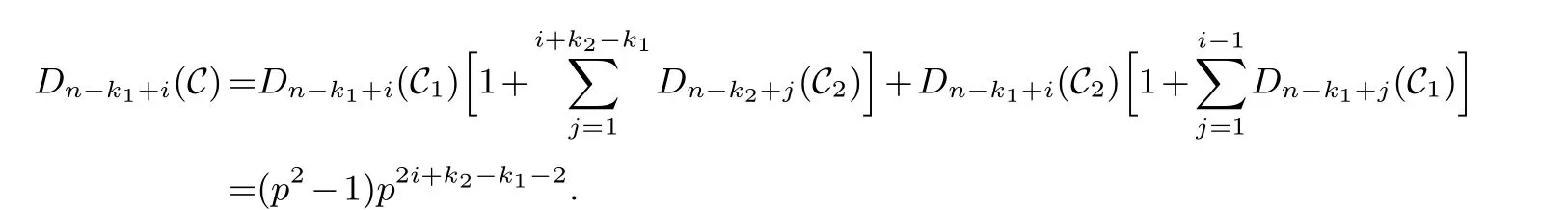

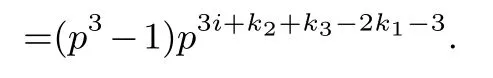
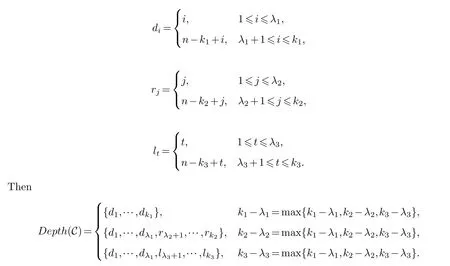
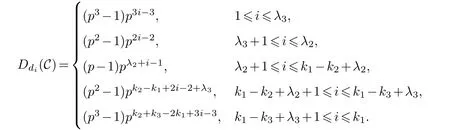
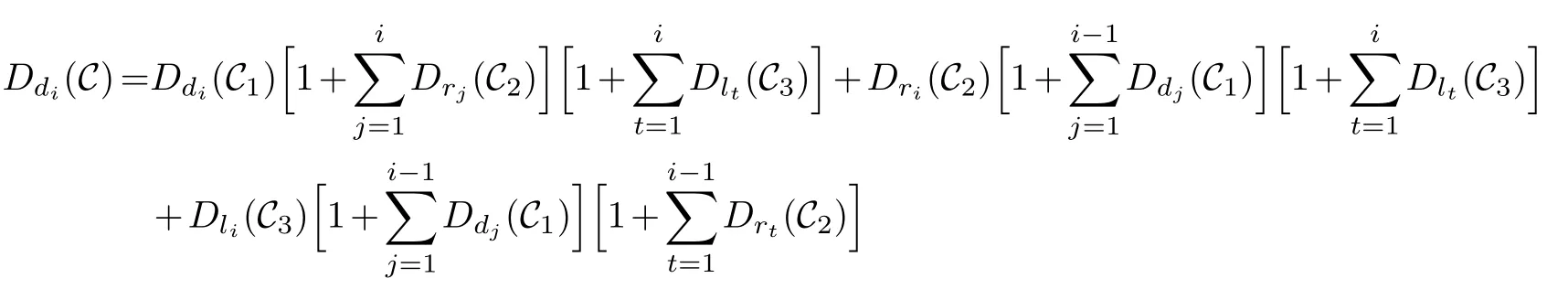
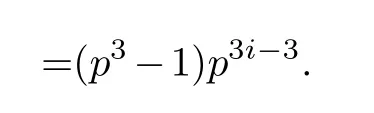
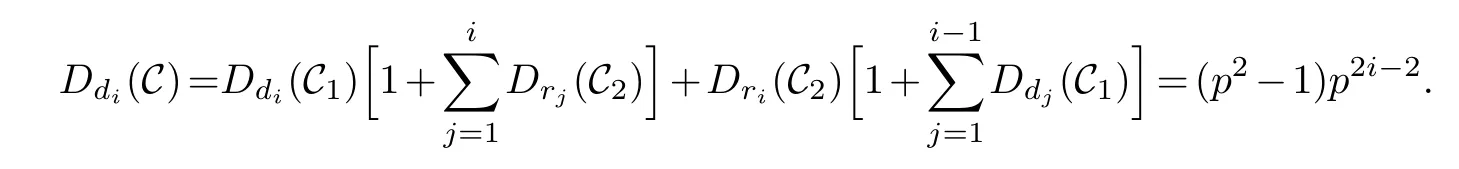
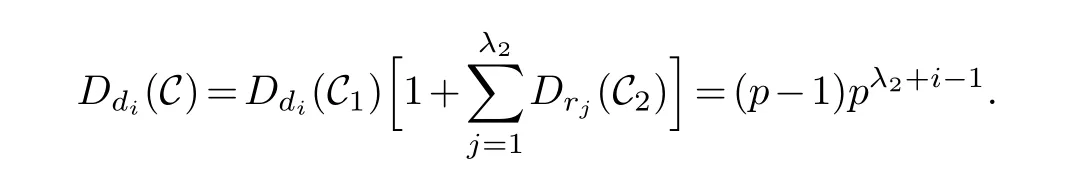
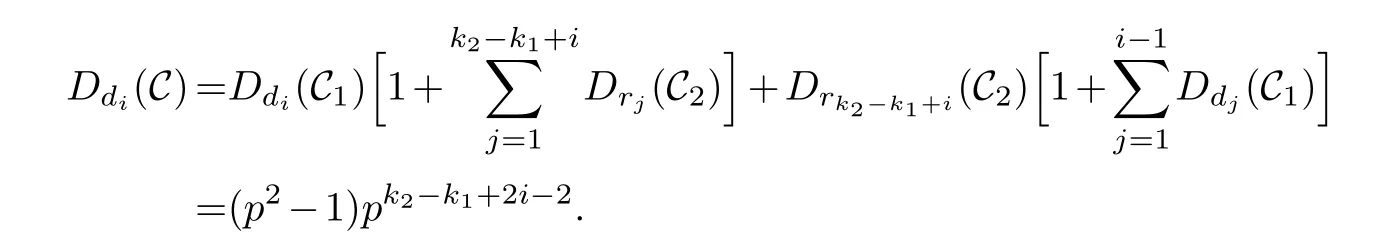
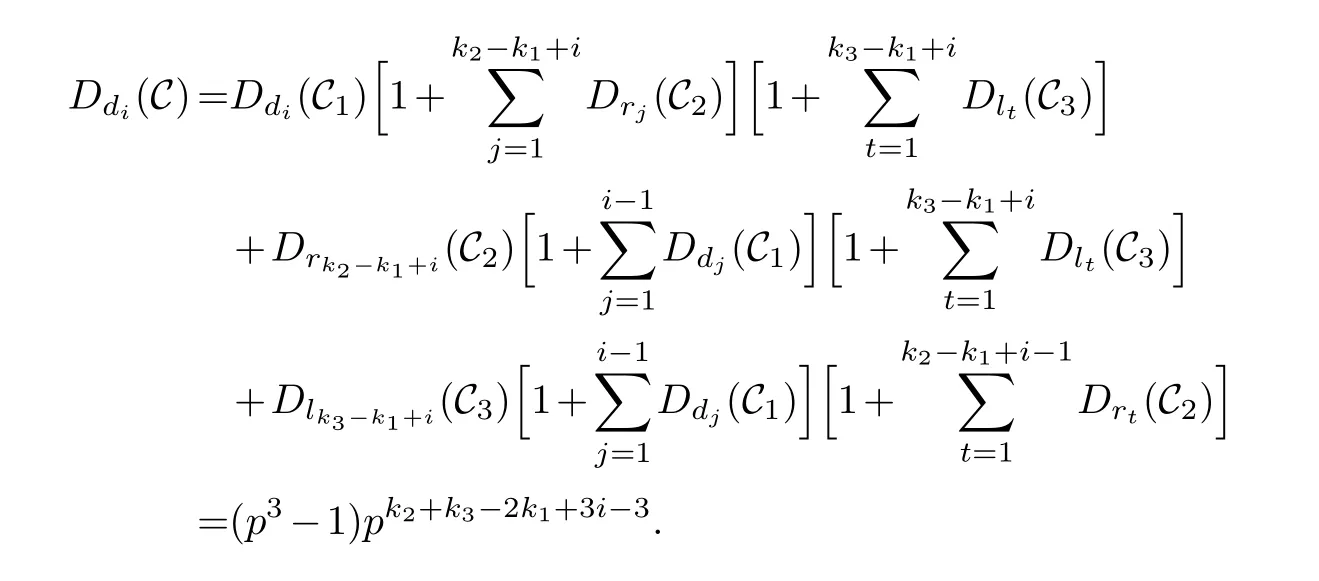
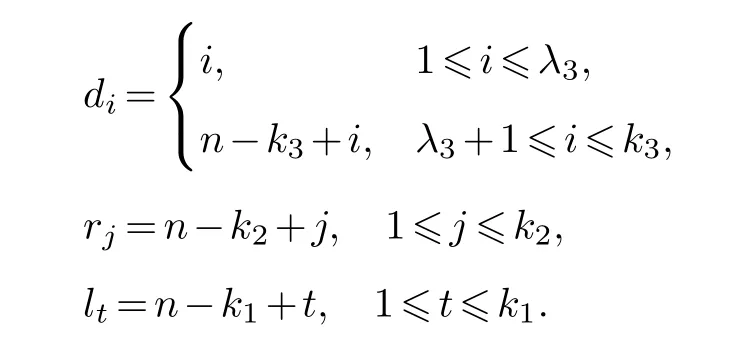
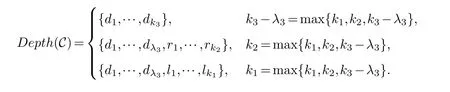
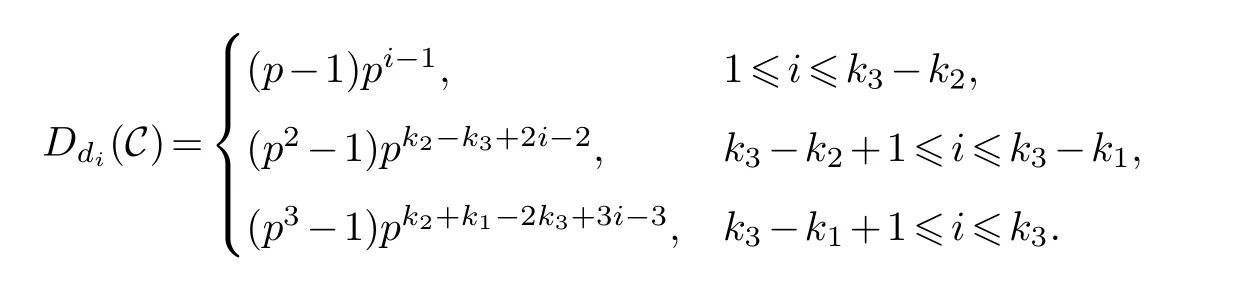
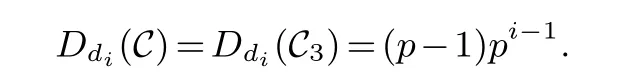
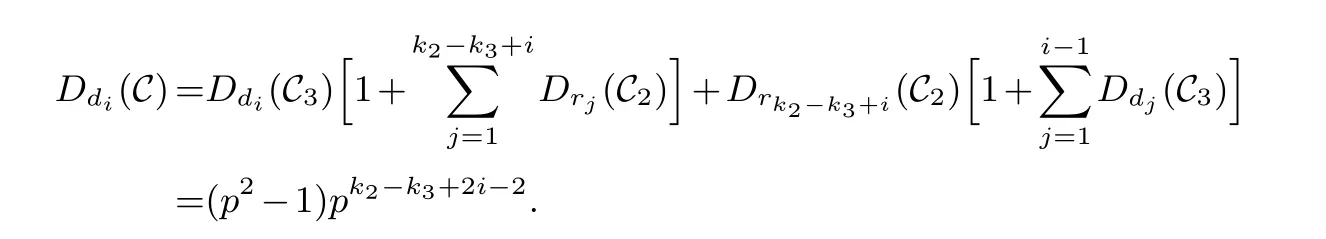
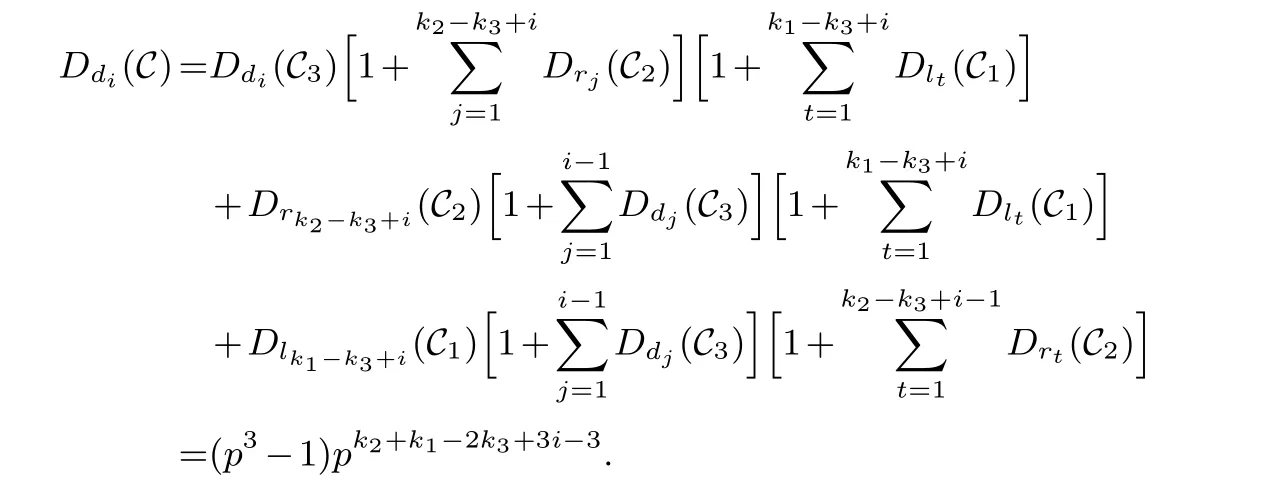

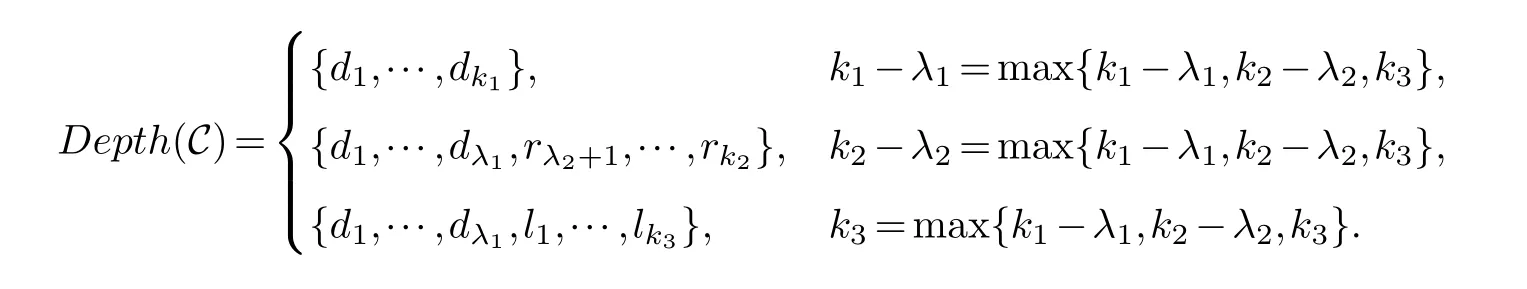
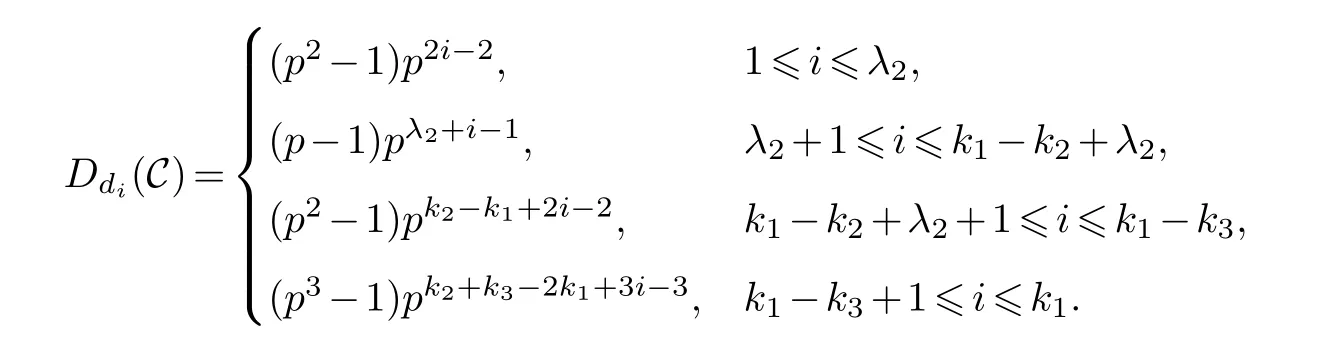
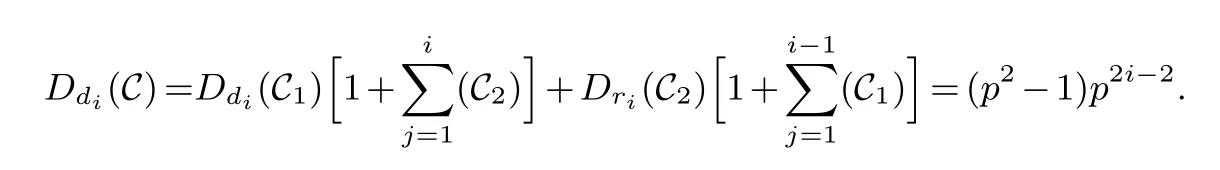

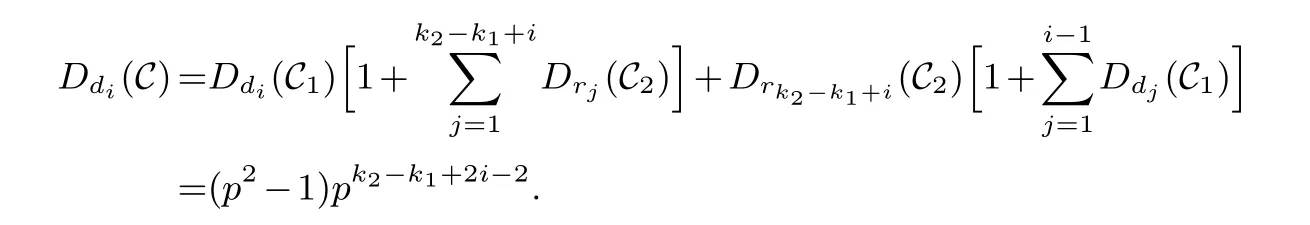
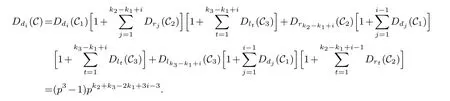
§5.Conclusion
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- The Integral Representations and Their Applications on the Analytic Varieties of Bounded Domains in Stein Manifolds
- An Efficient Algorithm for Low Rank Matrix Restoration Problem with Unknown Noise Level
- Triple Positive Solutions to a Third-Order m-Point Boundary Value Problem
- Uniqueness of Entire Functions Concerning Differences
- N-Width for Some Classes of Periodic Functions
- Phragm´en-Lindel¨of Alternative Result of the Forchheimer Equations
