基于代理模型与遗传算法的翼型优化设计方法研究＊

王璐瑶 于佳鑫 王晓东 陈江涛 吴晓军

（1.华北电力大学电站能量传递转化与系统教育部重点实验室；2.中国空气动力研究与发展中心）

0 引言

风力机翼型是风力机叶片设计的基本元素。翼型的气动性能关系着风力机的风能吸收效率。翼型气动优化设计方法分为两种：正设计法与反设计法。正设计方法主要以翼型的一个或多个气动特性为目标函数，采用优化算法求解最优翼型。反设计方法通常给定翼型表面压力分布来反推符合该压力分布的翼型几何外形[1]。其中，正设计方法不需要根据经验预先给定压力分布等参数，因此近年来得到了快速发展。

随着计算流体力学（CFD）模拟的快速发展，CFD 已经成为翼型设计中进行气动性能评估的主要手段。杨科[4]等人提出了一种基于CFD 数值计算与遗传算法相结合的方法，对升阻比进行优化，结果显示翼型在多个工况下，气动性能得到提升。但CFD 方法通常计算周期长，计算量大。因此在优化设计中需要的计算量很大。有研究者尝试将机器学习理论应用到CFD计算中，提出了基于人工神经网络等代理模型方法代替CFD 计算。王邦祥[6]等人提出了一种基于CFD 和神经网络的翼型优化方法，将翼型在三个工况下的升阻比通过线性加权的方式结合作为目标函数。遗传算法寻优时，利用神经网络计算代替CFD计算，大大减少了计算量。杨硕[7]建立了径向基函数模型耦合多目标粒子群优化算法的翼型多目标（多工况）优化设计方法，以升力系数和升阻比为优化目标，对翼型进行单目标和多目标优化。琚亚平[8]等人采用人工神经网络建立代理模型，结合遗传算法对FX63-167 翼型进行优化。优化结果显示此种优化方法可以缩短优化时间，提高优化效率。但是代理模型的预测精度会对最终优化结果产生影响。为了提高代理模型的预测精度，需要相当数量的训练样本。黄意坚[9]等人提出了一种基于代理模型的优化方法，通过不断增加训练样本来提高代理模型的预测精度，对平底后缘翼型进行单目标优化，结果显示在设计工况下，翼型升力系数提升了8.35%。王晓东[10]等人提出了一种基于非确定性计算流体动力学(CFD)仿真结合多目标遗传算法(MOGA)的鲁棒气动优化方法，文章指出当训练样本不充足时，BP神经网络的预测精度不高；而当训练样本数量过大时，样本的计算量又过大。因此，如何提高代理模型的精度和训练效率是此类气动优化方法的关键。Hirsch[13]等提出了一种coarse-to-fine 的逼近策略，采用单目标优化，将优化结果加入样本库，通过迭代提高逼近模型的预测能力。Nain 和Deb[11]提出一种类似的coarse-to-fine 迭代方法，基于多目标优化方法NAGA-Ⅱ和神经网络，将每次得到的Pareto 近似解加入样本库重新训练代理模型，预测精度逐渐提高，优化结果逐渐收敛到Pareto 前沿。经验证此种迭代方式在不同的问题上可减少约30%～80%的计算工作量。王晓东[12]等采用coarse-to-fine 的迭代策略，并对NSGA-Ⅱ与前馈式神经网络的耦合优化方法对Rotor37进行三目标的气动性能优化，探讨了coarse-to-fine 策略对多目标优化收敛性的影响[14]。

本文以S809风力机翼型为对象，建立了运行工况点下优化目标为升力系数的优化模型，采用coarse-tofine 迭代策略，利用参数化方法、计算流体力学(CFD)、基于神经网络的代理模型和遗传算法相结合的方法进行优化设计。重点讨论coarse-to-fine 策略中初始样本数与细化迭代次数的关系，检验coarse-to-fine策略对于提高代理模型的预测精度和减少计算量的效果。

1 数值方法

1.1 翼型的几何参数化模型

在翼型优化过程中，每一次优化都需要对翼型的几何进行改变。采用参数化方法可以代替型线散点，以较少的参数表示翼型的几何，方便改变几何形状。翼型几何参数化方法有样条参数化方法[15]，PARSEC参数化方法[16]和CST（Class function/ Shape function Transformation，CST）方法[17]等。其中，CST 参数化方法精度较高，参数少。因此，本文采用CST 参数化方法。CST参数化方法由形函数和类函数组成。如

上表面型线可以表示为：

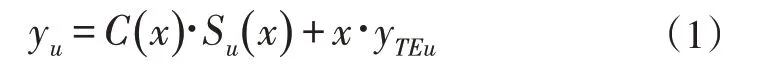
下表面型线：

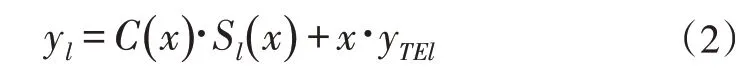
式中，下标u，l分别表示翼型的上下表面；yTEu，yTEl分别为上下表面后缘的y坐标。类函数C(x)定义如下：

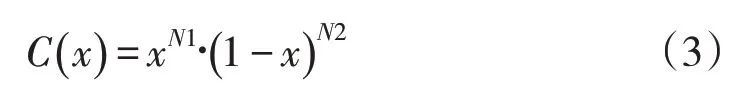
类函数控制翼型的种类，N1，N2 为类函数参数，对于一般翼型，分别取0.5，1。形函数S(x)对翼型的外形进行修正，形函数的基函数常用Bernstein 多项式。Bernstein 多项式的阶数越高，拟合效果越好，但是拟合所需参数数量随之增加。图1给出了S809翼型在4 阶Bernstein 多项式时的拟合情况，可以看出拟合效果很好。所以本文选择4 阶的Bernstein 多项式对S809翼型进行拟合。

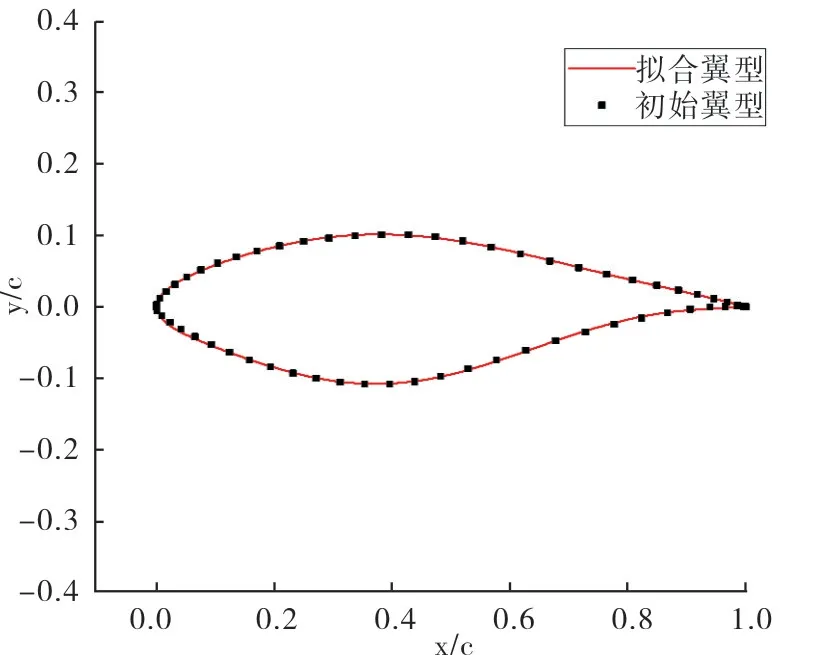
图1 S809翼型的拟合结果Fig.1 Fitting results of S809 airfoil

1.2 CFD模拟方法

翼型的气动力采用二维的CFD计算来获得。采用开源软件OpenFOAM 进行二次开发。选取OpenFOAM自带的结构化网格划分工具blockMesh 进行批量网格划分，通过Python编写网格批量生成程序。

计算域形状为C 型，并对翼型近壁区域进行加密，翼型周向节点数为480，C 型区域径向节点数为75，方形区域x及y方向节点数均为200，翼型表面的首层网格高度满足y+小于1，网格数为7.35 万，整体网格和翼型周围的网格如图3 所示。雷诺数Re=1×106，不可压缩空气的粘度ν为1.57×10-5Pa·s，密度ρ=1kg/m3。

进口采用速度进口边界条件，出口采用压力出口，翼型表面为无滑移，光滑壁面；湍流模型采用SST k-ω 模型。采用稳态不可压缩流求解器SimpleFOAM。残差收敛精度设置为10-6。

1.3 代理模型

在气动分析方面，由于模拟计算量大，计算时间长，在需要大量样本计算的情况下，消耗的计算资源和时间过长[24]。代理模型是将CFD 计算的样本作为训练数据进行学习。经过训练的代理模型，可以代替CFD 给出新的样本的性能预测。预测精度通常随训练样本数的增加而提高[17]。

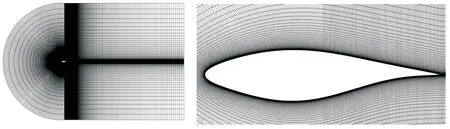
图2 计算网格及翼型附近网格Fig.2 Computational mesh and the details of the grid near airfoil surface

径向基神经网络RBFNN（Radial basis function neural network）可以拟合非线性函数，对学习样本之外的个体预测精度较高，泛化能力很强，所以本文采用径向基神经网络[8]。本文神经网络的输入为样本翼型的9 个CST 参数化参数和对应的升阻力系数，输出为参数化参数和升阻力的一种近似映射关系。为了保证训练样本对设计空间的覆盖性，本文采用拉丁超立方方法生成160组初始训练样本，160组样本中150组样本用于训练神经网络，剩余10组用来测试神经网络的预测精度。10组预测样本的升力系数和阻力系数预测的平均相对和绝对误差如表1，相对误差为代理模型对优化翼型升阻力的预测值相对于CFD计算值的误差。误差精度都达到了10-3量级，由此看出，RBFNN的预测精度比较高。

表1 RBF对升阻力预测的绝对与相对误差Tab.1 Absolute and relative errors of RBF in predicting lift resistance

1.4 优化算法

智能优化算法主要包括遗传算法、模拟退火算法、粒子群算法、差分进化算法[25]等，其中遗传算法的选择、交叉、变异具有意义明确，实施简单等优点，是一种高效，并行，全局搜索的方法，在优化过程中，可以获得比较好的全局最优解。因此，本文采用了遗传算法[18]。遗传算法在编码[21]的基础上，生成初始种群，计算种群中每个个体的适应度，进行基因的复制，交叉和变异现象，并且遵循适者生存的原则，在满足条件的种群中逐次产生一个最优的个体，种群得以进化，最终得到一个最优的个体。

1.5 Coarse-to-fine的迭代策略

代理模型的预测精度受样本数量影响很大，而增加训练样本的数量就会增加计算量。本文利用一定数量的初始样本对代理模型进行训练，每次优化得到的翼型要比初始样本更接近最优解，将优化结果添加到初始样本中对代理模型进一步训练，优化得到的翼型都较前一次更准确，最终优化结果会收敛于最优解，减少了计算量。为了区分coarse-to-fine 的迭代与遗传算法的进化迭代，将coarse-to-fine 迭代称为外部循环。

综上所述，翼型的气动优化设计可以分为以下几步：

①选择翼型的参数化表示方法及设计变量；

②应用试验设计法在设计空间内生成一定数量的样本；

③对样本进行CFD计算得到每个翼型对应的升阻力；

④将每个翼型对应的参数化参数和升阻力组成训练样本训练代理模型，得到参数化参数和升阻力的对应关系；

⑤在设计空间内随机生成初始样本，基于代理模型求得目标函数的最优值，并通过遗传算法迭代求得最优翼型。

如图3所示，为气动优化设计流程图。

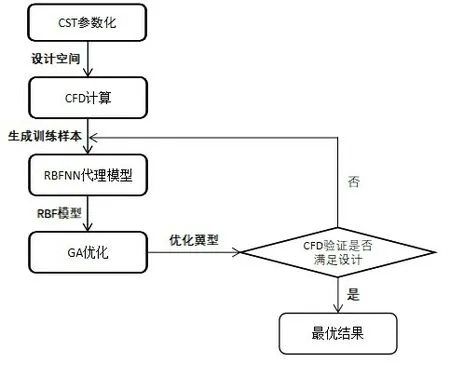
图3 带coarse-to-fine循环的翼型气动优化过程Fig.3 Aerodynamic optimization process of airfoil with coarse-to-fine iterations

2 S809翼型气动优化设计

2.1 优化模型

本文采用S809 翼型为基准翼型，以α=12°，v=15.7m/s为设计点进行气动优化设计，S809翼型的气动优化问题可表示为：目标函数为翼型升力系数最大，约束条件为翼型最大厚度不变，最大厚度相对位置变化范围为±5%，设计阻力系数小于原始翼型S809 的阻力系数。

优化变量：参数化方法选取4 阶Bernstein 多项式，选取9 个设计变量来确定翼型的几何形状，上表面设计变量为a0,u，a1,u，a2,u，a3,u，a4,u，下表面设计变量为a1,l，a2,l，a3,l，a4,l，设计变量范围设置为原翼型变量数值上下50%，取值范围见表2。图4为翼型上下表面控制点位置，图中实线为原翼型拟合结果。

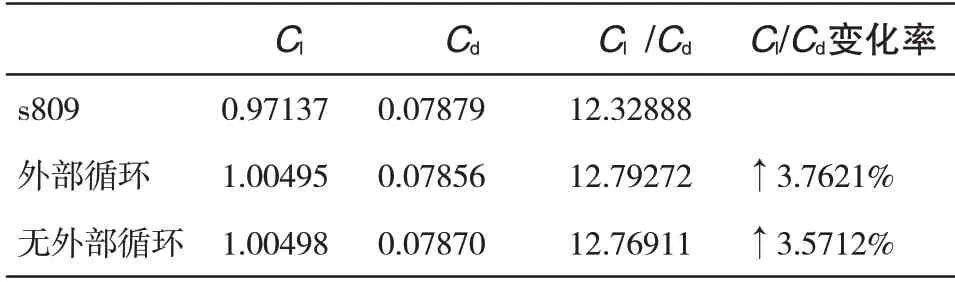
表2 原翼型和优化翼型的升阻比对比Tab.2 Contrast of lift-drag-ratio of original and optimized airfoils

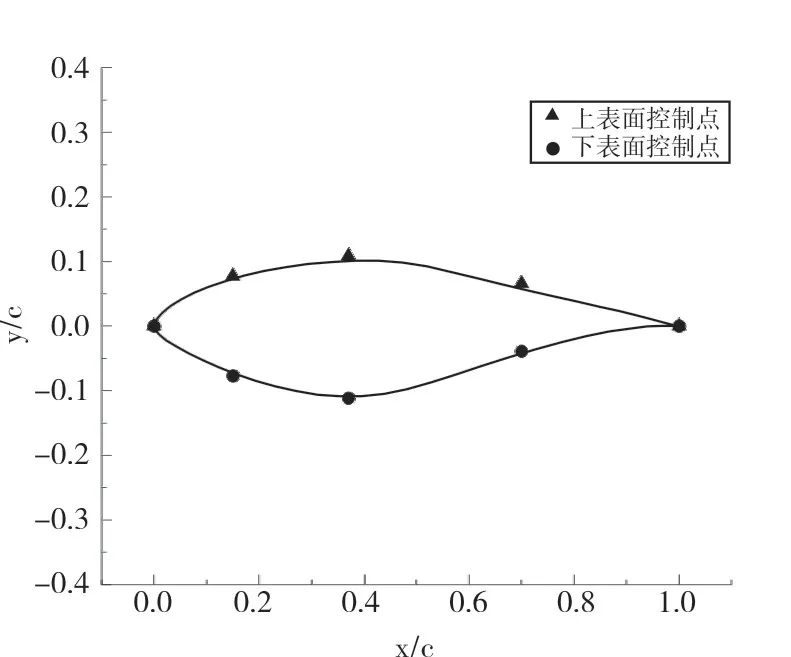
图4 翼型上下表面控制点Fig.4 Control points on the upper and lower surfaces of the airfoil

控制参数种群规模为40，父母数为20，交叉概率为0.5，变异概率为0.001，最大进化代数为400。图5为外部循环次数与初始样本数的关系曲线。从图中可以看到，随着初始样本数的增加，迭代次数逐渐减少，但是总的计算量也在增加。初始样本数为20 时，外部循环次数为39次，总计算量为59；初始样本数为150 时，外部循环次数为8 次，总计算量为158，远大于样本数为20时的计算量。图6为总计算量与初始样本数的关系曲线，从图中可以看到在初始样本数为20时，总计算量达到最小。所以选取20为最优的初始样本数，图7 给出了初始样本数最优情况下，外部循环过程中升力与阻力相对误差收敛曲线，相对误差为代理模型对优化翼型升阻力的预测值相对于CFD计算值的误差。

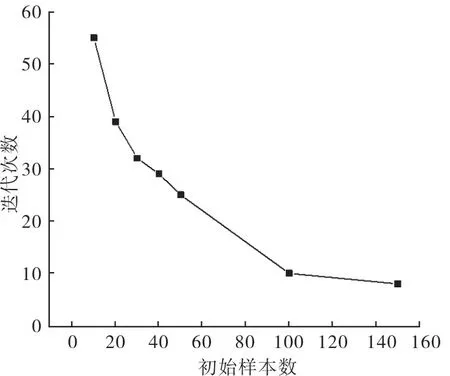
图5 迭代次数随初始样本数变化曲线Fig.5 Curve of iteration number changing with initial sample number

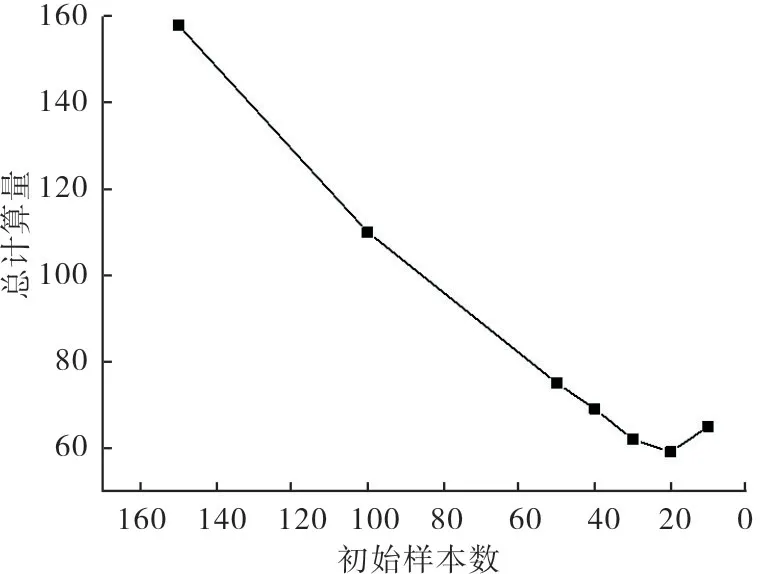
图6 总计算量随初始样本数的变化曲线Fig.6 Curve of total calculation quantity changing with initial sample number

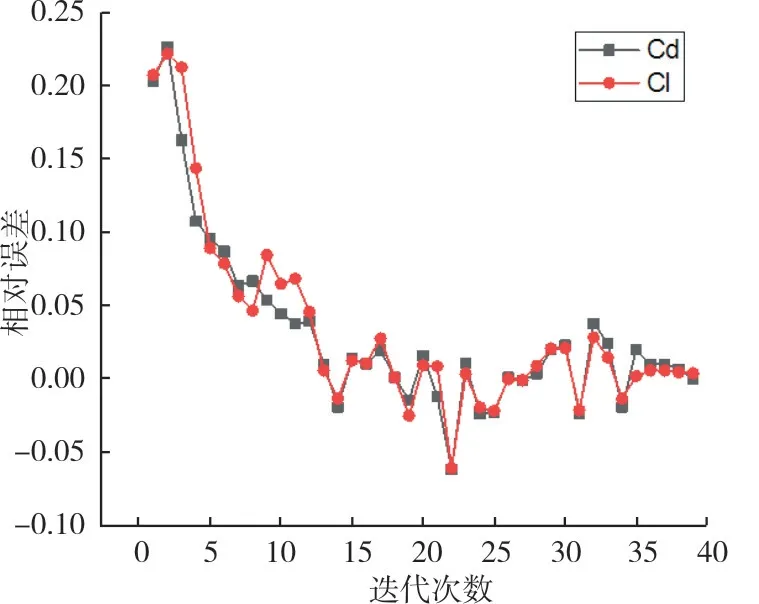
图7 升阻力相对误差收敛曲线Fig.7 The convergence curve of the relative error of lift and drag

2.2 优化结果分析

基于上述优化方法进行计算求解，外部循环方法的初始样本数为20，经过39次迭代得到优化结果，总计算量为59次，无外部循环的样本数为150。结果表2给出了两种优化方法下，优化前后翼型的升阻力对比。由表可知，优化后的翼型升阻比较优化前均有所增加。有外部循环的翼型升阻比较无外部循环的升阻大，升阻比变化率也高于无外部循环的结果，验证了coarse-to-fine 策略在减少计算量的同时获得气动性能更优的优化结果。

表3 给出了两种优化方法下，代理模型对优化翼型升力与阻力的预测精度对比。对比发现代理模型对升力与阻力的预测精度均达到了10-3。对于升力系数，有外部循环的相对误差较无外部循环要小，验证了coarse-to-fine 策略对于提高代理模型的预测精度的有效性。

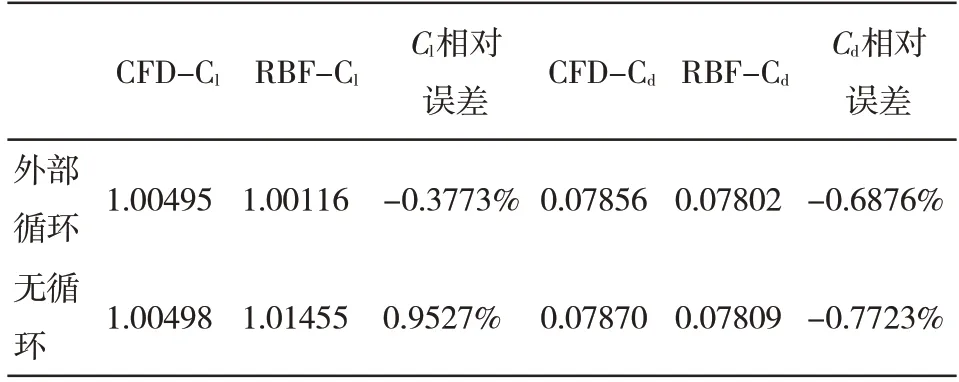
表3 神经网络对优化翼型升力与阻力预测精度对比Tab.3 Comparison of prediction accuracy of lift and drag of optimized airfoil by neural network

图8 给出了有无外部循环下优化翼型与S809 翼型的几何对比。可以看出在两种优化方法下，优化后的翼型的最大厚度较原翼型变化较小，但是最大厚度的相对位置向前移动，有外部循环的优化翼型前缘变厚，尾缘比跟原始翼型相差不多，无外部循环的优化翼型尾缘附近变厚。

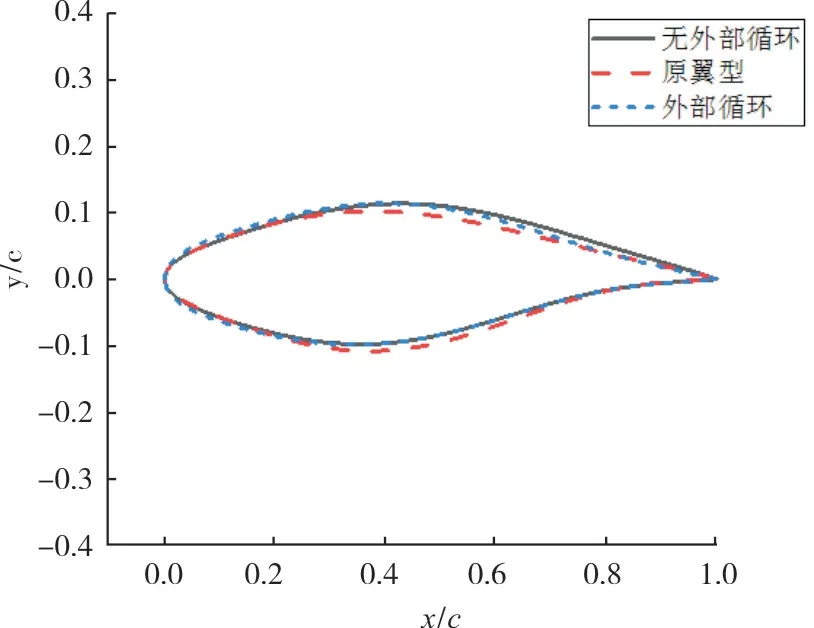
图8 优化前后翼型形状对比Fig.8 Contrast of airfoils before and after

图9 给出了优化前后翼型的表面压力系数分布对比图。从图中可以看出，优化后的翼型吸立面压力分布曲线交优化前更光顺。无外部循环的结果在吸力面中段出现了压力平台，表面流动发生了分离。压力面的压力系数变动不大。优化后的翼型压力曲线在翼型中后段围成的面积比原翼型大，上下表面压差增大，表明翼型载荷后移。

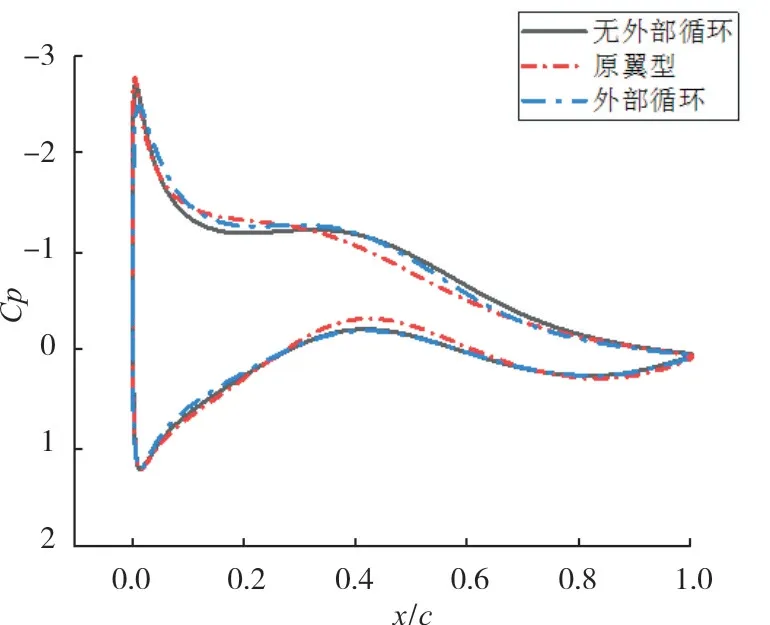
图9 翼型表面压力系数分布对比图Fig.9 Contrast of pressure Coefficient of airfoil surface

图10 为有外部循环的情况下，迭代10 次和迭代25次得到的翼型与原翼型的流线对比，可以看出第10次和第25次迭代得到的优化翼型较原翼型吸力面的分离区明显减小，分离位置靠后，涡结构减小，推迟流动分离。

图10 原始翼型和优化翼型的流线比较Fig.10 Streamline comparison of the original airfoil and the optimized airfoil

3 结论

1）本文采用coarse-to-fine迭代策略，利用CST参数化方法，基于神经网络的代理模型、遗传算法结合的优化方法对S809翼型进行优化设计，计算效率比较高。优化后的翼型载荷后移，吸力面分离减小，升力提升，阻力降低，气动性能更佳。

2）有外部循环的优化翼型升阻比较高，说明其获得的优化结果的全局最优性更大。代理模型对优化翼型的预测精度较无外部循环情况下要小。有外部循环时，计算的总样本数减小，计算量减少；从循环迭代过程中看到，翼型升阻力相对误差逐渐减小，证明添加外部循环的有效性。