基于水平时谐电偶极子模型的舰船轴频磁场传播特性分析

庞 鑫，刘忠乐，文无敌，林朋飞，林 嘉，唐琼婕，史润泽

(1.海军工程大学 兵器工程学院， 武汉 430033； 2.山东省军区数据信息室，济南 250000； 3. 75222部队，福建 泉州 362000； 4. 32382部队， 武汉 430033)

由于舰船中含有不同材料的金属结构件，加之海水是良导体，不同材料的金属在海水中容易相互之间发生电化学反应，从而产生腐蚀电流，进一步腐蚀舰船船体[1]。为了减小腐蚀电流对船体的腐蚀，通常采取加入保护电流的方法，有外加电流的阴极保护法和牺牲阳极保护法[2]。当船体的腐蚀电流和防腐电流流向舰船的螺旋桨主轴时，被一定转速的螺旋桨经过周期性调制后，经轴承再回到船体形成电流回路。舰船螺旋桨会调制流经的腐蚀电流和防腐电流产生时变电流，该电流的基频就是螺旋桨的转动频率，而轴频电磁场由时谐电流信号产生[3-4]。由于轴频电磁场信号的频率与螺旋桨转速有关，一般为几个赫兹，区别于工频电磁场信号、环境电磁场信号，且轴频电磁场相对于未加调制的腐蚀电磁场传播距离远。可见轴频电磁场是水中目标检测的重要目标之一，所以对轴频电磁场进行分析建模具有重要意义[5]。

熊露等基于水平时谐电偶极子的模型对浅海环境中的轴频电场进行了3层介质下的电场建模，推导了其在海水中的电场分布，试验结果和理论结果一致[6]。张立琛等基于磁偶极子模型对舰艇水下轴频电磁场进行建模，减小了计算量和实测数据量[7]。陈聪等基于静态电偶极子对海水中的静态电场和磁场分布进行了建模[8]。孙玉绘等将轴频电流等效为垂直时谐电偶极子进行了三层介质下的磁场建模，求得了其在空气中的磁场分布，验证了实用性和有效性[9]。卢修宇基于多个水平电偶极子对海下磁异常目标的防腐蚀电流电磁场结合实际情况所需进行研究分析，准确计算出了典型水下防腐蚀电流源在空间中产生的异常场分布，为水下或者航空磁探与识别提供参考信号样本[10]。黄凡通过麦克斯韦方程推导出了在海水中的水平时谐电流段在空气层中产生的磁场理论公式，仿真结果表明该过程能较好利用轴频电场来探测水下潜艇[11]。以上文献只单一地对轴频电磁场信号的在海水或空气中的分布做了建模分析，大部分只集中在水中磁源在海水中的磁场分布，这限制了同时在海水与空气中进行轴频磁场探测的发展。本文基于水平时谐电偶极子对舰船轴频磁场在海水中和空气中产生的磁场进行了系统建模，理论上为船舶的轴频磁场在海水和空气中的传播特性提供了依据，同时也为轴频信号探测提供了理论基础。

1 舰船轴频磁场相关理论分析

基于水平时谐电偶极子对舰船轴频磁场进行建模，假设空气与海水为各向同性、线性、均匀的半无限媒质空间[12]。两者之间的交界面为无限大的平面。水平时谐电偶极子的矢量磁位沿x轴方向，电偶极子位于下半空间(z<0)x方向，处于点z0(x′，y′，z′)。上半空间(ε1，μ1，γ1)，下半空间(ε2，μ2，γ2)，则其模型如图1所示。

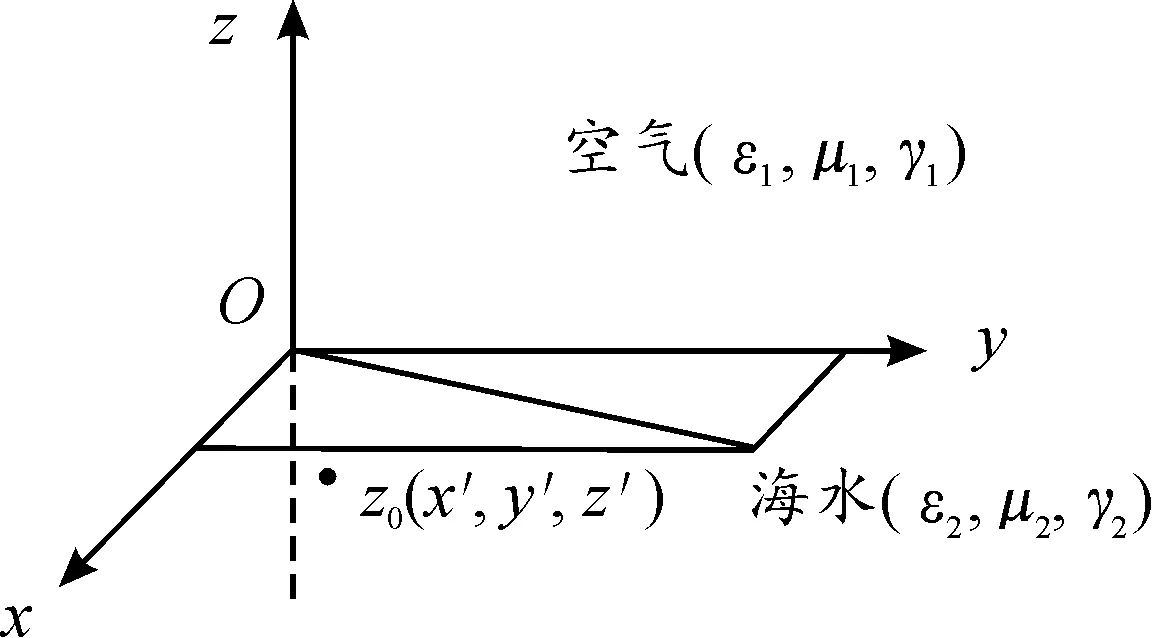
图1 水平时谐电偶极子模型示意图

1.1 矢量磁位

利用镜像法求解，可以得到在海水中x方向的水平电偶极子在上、下半空间产生的矢量磁位公式[13]：

A1=A1x·i+A1z·k=

H·J1(λρ)·k]·eu2z′-u1zdλ(z>0)

(1)

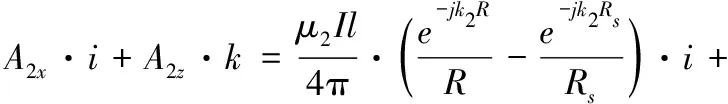
H·J1(λρ)·k]·eu2(z′+z)dλ(z<0)

(2)

其中，

J0是第一类零阶贝塞尔函数，J1是第一类一阶贝塞尔函数。其中空间中任一位置的坐标为(x，y，z)，为水平时谐电偶极子的角频率。

由矢量磁位公式可以看出，水平电偶极子不仅产生同方向的矢量磁位Ax，而且还产生与空间边界面互相垂直的矢量磁位Az。

1.2 水平电偶极子在海水中产生的磁场模型

设上半空间为真空，下半空间为线性、均匀、各向同性的非磁媒质。低频时谐电偶极子位于下半空间r′=x′i+y′j+z′k，真空中磁导率μ0=4π×10-7H/m，海水磁导率等于真空中磁导率。设真空区为1区，海水区为2区。

1区真空中：μ1=μ0，ε1=ε0，γ1=0，k1=0。

2区海水中：

由麦克斯韦方程组可知

(3)

1.2.1海水中i方向电偶极子在上半空间产生的磁场强度

设海水中i方向水平时谐电偶极子在上半空间的磁场强度为：

H1=H1x·i+H1y·j+H1z·k

(4)

由于k1=0，依据式(3)和矢量磁位式(1)得到位于下半空间的水平时谐电偶极子在上半场的磁场分布为：

(5)

1.2.2在下半空间中产生的磁场强度

设海水中i方向水平时谐电偶极子在下半空间的磁场强度为：

H2=H2x·i+H2y·j+H2z·k

(6)

由于k1≠0，依据式(3)和式(2)得水平时谐偶极子在下半场的磁场分布：

(7)

其中，空气中介电常数ε1=ε0，海水中介电常数ε2=81ε0，空气与海水中的磁导率为μ1=μ2=4π×10-7H/m，海水中的电导率γ2=4 s/m，空气中电导率为0。I0为第一类零阶修正贝塞尔函数，K0是第二类零阶修正贝塞尔函数，J0是第一类零阶贝塞尔函数，J1是第一类一阶贝塞尔函数。

根据广义索末菲积分的解析式和计算式，可以对水平电偶极子的磁场模型进行计算[14-15]。

2 模型仿真分析

2.1 海水中的磁场仿真

假设水平电偶极子的坐标位置为(0，0，h)，h=-5 m，仿真在y=30 m，水深z=-30 m交界线上，x在[-500，500]范围内磁场分布情况。设船速为5 m/s，模拟源强度I·dl=100，空气中介电常数ε1=ε0，海水中介电常数ε2=81ε0，空气与海水中的磁导率为μ1=μ2=4π×10-7H/m，海水中的电导率γ2=4 s/m，空气中电导率为0。一般轴频电磁场频率为2～5 Hz，取为5 Hz。

由图2可见水平电偶极子在x、y、z三个分量上的磁场分布Bx、By、Bz以及总磁场分布B。其中x分量的磁场强度Bx有方向变化。

在不同水深情况下进行仿真轴频磁场的分布，设在水平面下-15 m，-30 m，-45 m三个不同水深下，即在y=30 m，水深z分别为-15 m、-30 m和-45 m水平面的交界线上，x在[-500，500]范围内磁场分布情况，仿真如图3所示。

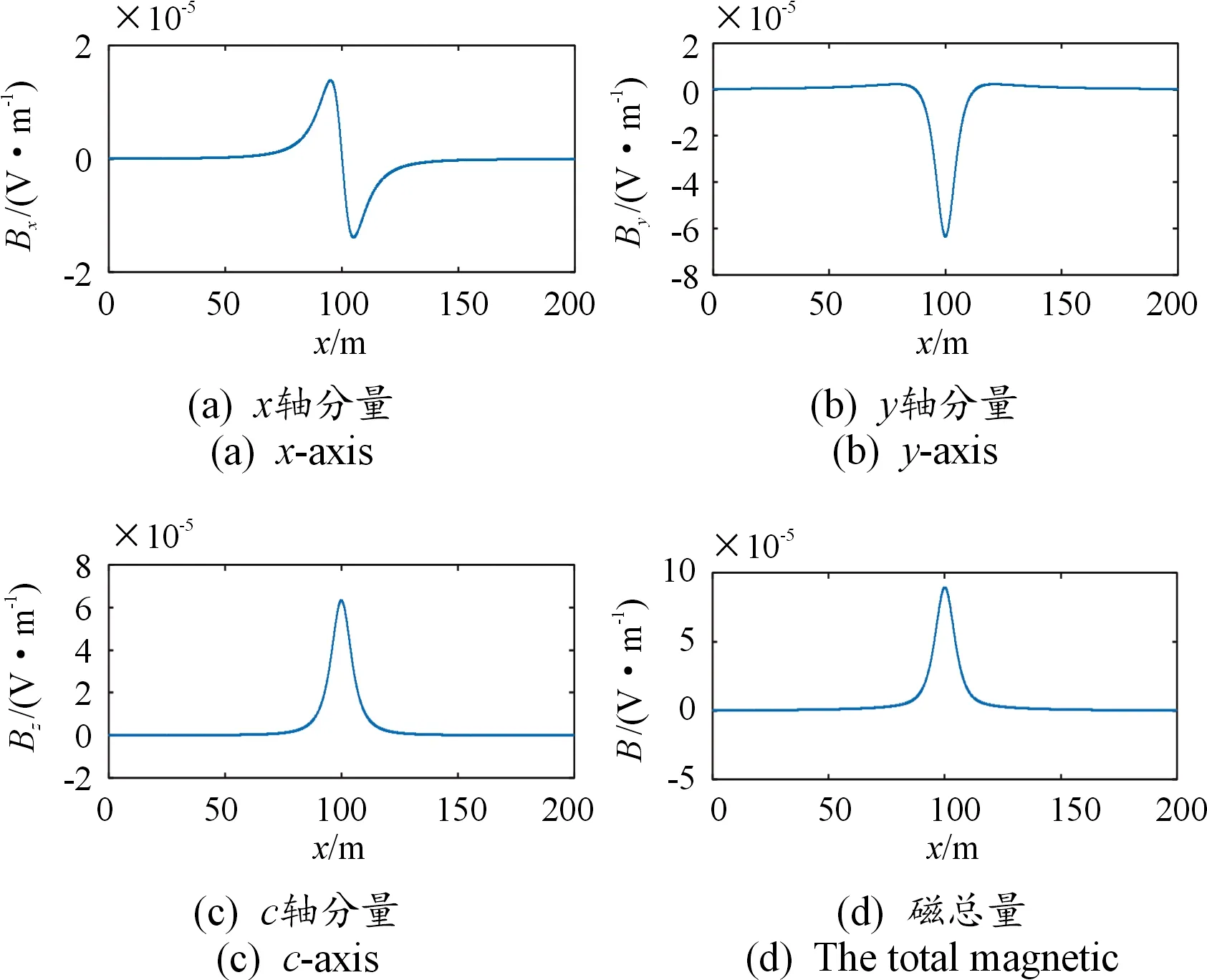
图2 水平时谐电偶极子在海水中磁场及其 三分量分布曲线

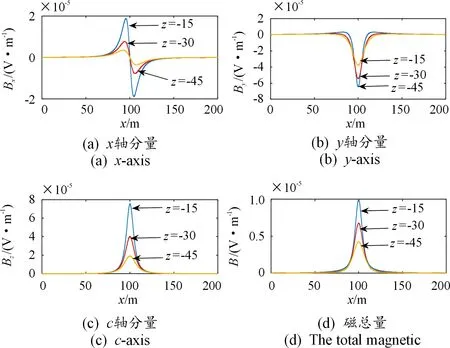
图3 水平电偶极子在海水中不同深度下的 磁场分布曲线

由图3可以得出，随着远离场源点方向上深度的增加，磁场强度逐渐减小，当深度由15 m下降到45 m时，Bx分量最大绝对值由1.88×10-5减小到3.55×10-6，减小到15 m深时最大值的20%，而仿真By分量最大值绝对值由6.44×10-5减小到3.78×10-5，减少到58%，仿真Bz分量最大值绝对值由7.55×10-5减小到1.91×10-5，减少到25%左右。总磁场强度由9.93×10-5减小到4.23×10-5，减少到43%左右。可见By分量随着远离场源点方向上深度的增加，磁场衰减最小，在今后的轴频目标探测中，可以作为分析目标的重点。

2.2 空气中的磁场仿真

假设水平电偶极子的坐标位置为(0，0，h)，h=-5，仿真在y=30 m，空中距离水平面z=30 m交界线上，x在[-500，500]范围内电磁场分布情况。设船速为5 m/s，模拟源强度I·dl=100，空气中介电常数ε1=ε0，海水中介电常数ε2=81ε0，空气与海水中的磁导率为μ1=μ2=4π×10-7H/m，海水中的电导率γ2=4 s/m，空气中电导率为0。一般轴频电磁场频率为2～5 Hz，取为5 Hz。

图4即为水平电偶极子在x、y、z三个分量上的磁场分布Bx、By、Bz以及总磁场分布B。其中x分量的磁场强度Bx有较大幅度的方向变化。

图4 水平时谐电偶极子在空气中磁场及其 三分量分布曲线

仿真不同空中高度下，轴频磁场的分布，设在空气中5 m，25 m，45 m三个高度下，即在y=30 m，与空中高度z分别为5 m、25 m和45 m水平面的交界线上，x在[-500，500]范围内磁场分布情况，仿真如图5所示。

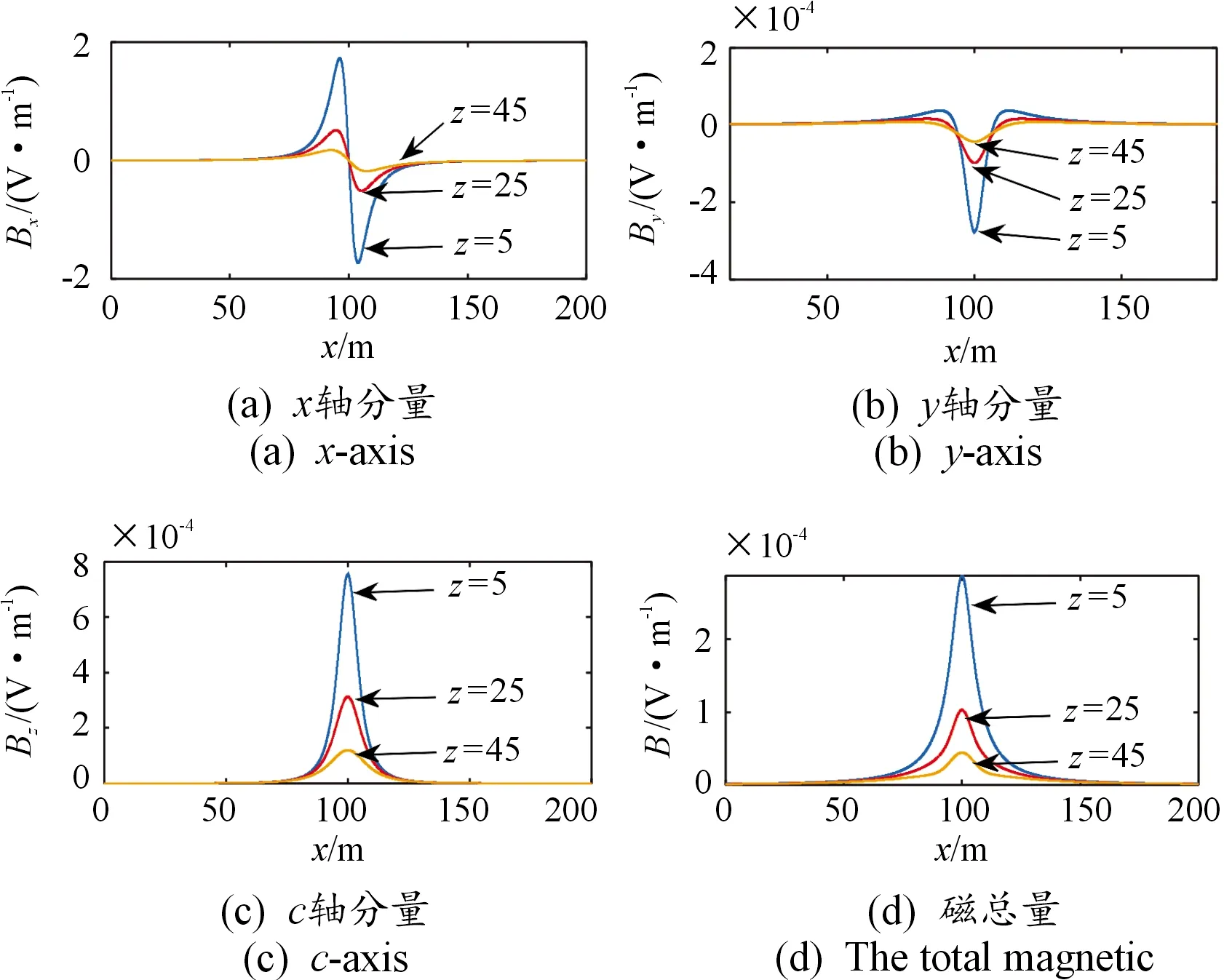
图5 水平电偶极子在空气中不同高度的磁场分布曲线

由图5可以看出，在空气中随着远离场源点方向上高度的增加，磁场强度逐渐减小，当高度由5 m增加到45 m时，Bx分量最大绝对值由1.72×10-4减小到1.78×10-5，减小到5 m高度最大值的10%左右，而仿真By分量最大值绝对值由1.72×10-4减小到1.78×10-5，减少到10%左右，仿真Bz分量最大值绝对值由7.55×10-5减小到1.20×10-5，减少到16%左右。总磁场强度由2.87×10-4减小到4.46×10-5，减少到15%左右。可见Bz分量和总磁场B随着远离场源点方向上高度的增加，磁场衰减较小，在今后的轴频目标探测中，可以作为分析目标的重点。

由于水中轴频磁场在空气中的磁场分布分析研究很少，可以相互对比分析的方法也有限，这在一定程度上限制了空中探测水下轴频磁场的发展。本节系统的分析了水下轴频磁场在海水中和空气中的磁场分布，将在下节实验结果中验证建模的合理性。

3 试验验证

由于理论分析的坐标系是以磁偶极子方向为x轴，磁场分布的三分量也是以所建坐标系为准，而实际实验中，海水中的轴频磁场坐标系并未确定，是以磁传感器的所测的三轴分量为准，其分别对应着理论分析的三分量。在对试验数据进行分析时，将实测数据所对应的x、y、z轴与理论坐标系中的x、y、z轴进行对应。

通过磁场特性曲线如图6所示。

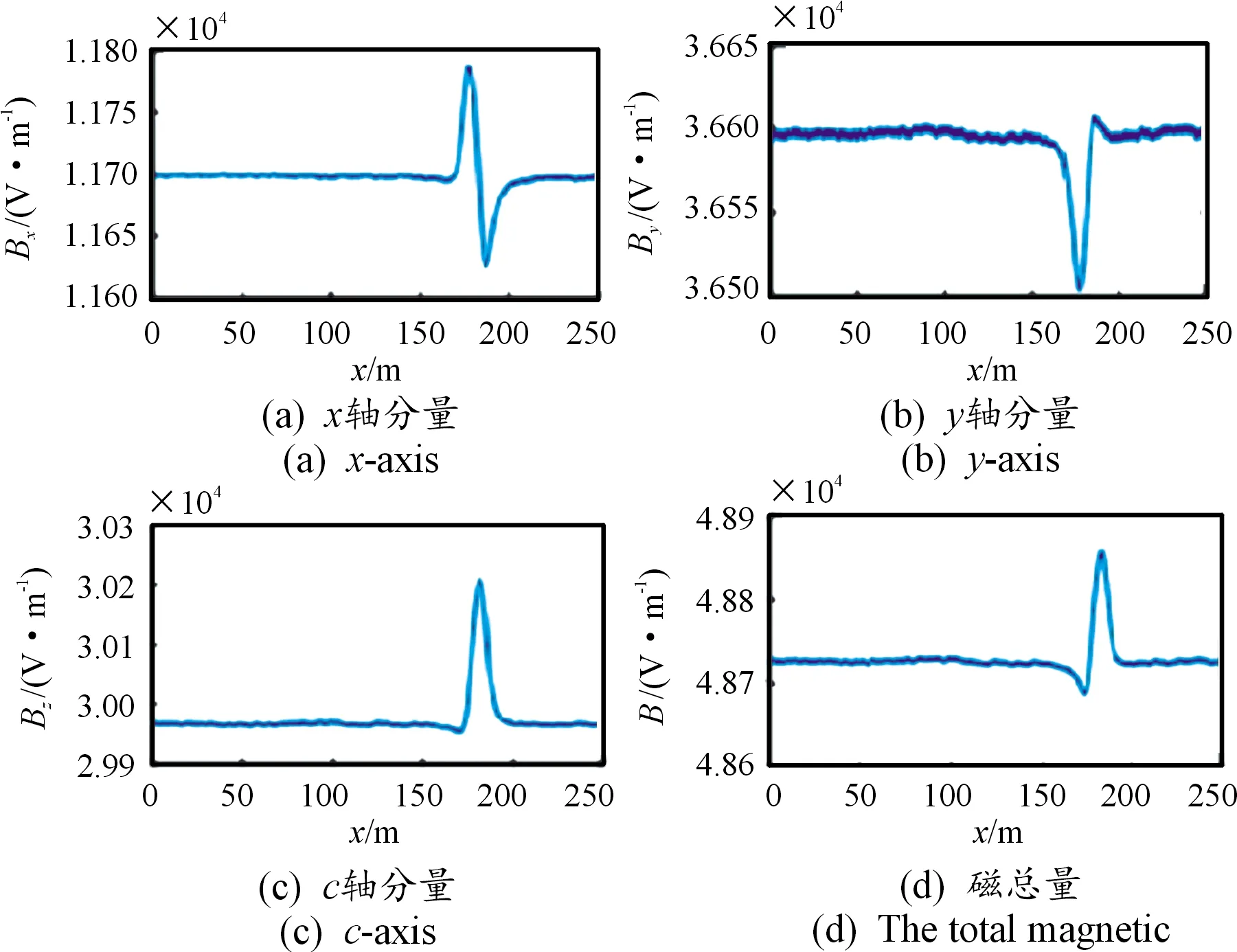
图6 实测船只通过磁场特性分布曲线

由图6可以看出，在空气中随着船只位置距坐标原点的增加，磁场强度呈现大幅度变化。当距原点175 m时Bx分量达到最大值1.18×104，By分量达到最小值3.65×104，Bz分量达到最大值3.02×104而总磁场B达到最小值4.868×104。当距原点190 m时，Bx分量达到最小值1.163×104，By分量达到最大值3.662×104，Bz趋于稳定而总磁场B达到最大值4.887×104。可以看出x、y、z三个分量上的磁场强度Bx、By、Bz随着船只位置的变化有较大幅度的方向变化且与所建空中模型的磁场分布曲线具有一致性，因此也验证了本文轴频磁场建模的可行性。

4 结论

1) 通过基于水平电偶极子对舰船轴频磁场进行建模分析，为在海水中和空中探测舰船轴频磁场提供了理论基础。

2) 分析了海水中水平时谐电偶极子在海水中和空气中的矢量磁位，由麦克斯韦方程组得到水平时谐电偶极子的磁场强度，仿真分析了水平时谐电偶极子在空气中和海水中磁场的分布特性。

3) 分析了水平电偶极子在海水中不同深度下和在空气中不同高度上，磁场三分量的变化趋势。

4) 验证了轴频磁场模型的可行性，为今后对舰船目标的探测提供了理论依据。