一种新式的电磁法管线探测仪
2022-01-10曹宏宇田前辉
曹宏宇,田前辉,王 云,刘 凯,王 盟,郑 刚
(河北科技大学 信息科学与工程学院,河北 石家庄 050018)
地下管线作为国家资源与信息传输的重要方式,在生活的各个方面都有着重要的作用。保障地下管线正常运作及安全关系到民生保障问题,所以显得格外重要。但随着地下管线的铺设,新旧管线交错在一起,且地下管线管理不规范,使得地下管线信息不完整,导致在施工过程中经常造成已铺设管线受损,造成巨大损失。因此,对地下管线的探测愈发重要。
目前,国内探测仪仍存在探测深度不够、定位不准,不能有效提供管线信息等问题,而国外探测仪器虽发展较成熟,探测效果较国内有巨大提升,但价格昂贵不适合于国内普遍使用。基于此种需求,笔者设计了一种无须开挖非接触式的,基于电磁感应法的管线探测仪,采用无损检测技术,达到对地下管线的有效探测。
1 电磁感应法探测原理
基于电磁法的地下管线探测仪,是遵循麦克斯韦电磁理论,通过电信号与磁信号的互相转化,达到对加在管线上的正弦交变信号的检测。进而获得有效的管线水平位置、埋深等信息。
地下管线其长度远远大于其管直径,所以可近似将其视为无限长的导线。向管线施加正弦交流电信号后,管线周围可产生与交流电信号同频的正弦交变磁场。天线电路上的感应线圈在感应到交变磁场信号后会转化成同样频率的正弦电信号。通过捕获后的电信号幅值与地下管线相对天线位置的对应关系,达到对地下管线的有效定位。
依据比奥-萨法尔定律,地下管线通入电流后,周围可呈现以管线为中心随半径而递减的磁感应强度[2、3]。管线产生磁场分布如图1所示。

图1 浓载流管道磁场模型
管线上方任意一点磁感应强度为:
(1)
式中:μ0—真空磁导率,(μ0=4π×10-1H/m);
r—点P到管线中心的距离;
I—管线通过电流强度。
依据矢量分解原理,可将磁感应强度分解为磁场水平分量Bx和磁场垂直分量By。
图2所示P点磁场水平分量Bx强度表达式为:
(2)
磁场垂直分量By强度表达式为:
(3)
1.1 管线水平定位
天线线圈在感应磁场后产生相对幅度且同频的正弦电压信号。依据不同方向天线线圈对Bx及By的感应信号值变化的不同趋势,可将水平定位方式分为波峰模式与波谷模式。
波峰模式是利用水平天线线圈所感应磁场的水平分量Bx,实现对地下管线的水平定位检测。当水平天线线圈位于地下管线的正上方时,线圈的感应电动势达到最大值,接收天线垂直于管线方向做横切运动,随着天线与管线的水平距离增加,线圈所产生的感应电动势呈左右对称的衰减趋势。这时,就会产生山峰一样的信号曲线,而其峰值位于地下管线的正上方[4]。图2和图3分别为波峰模式检测示意图及水平磁场分量在不同埋深下变化示意图。
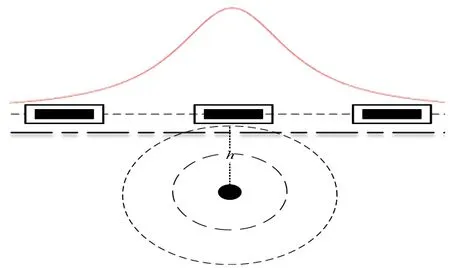
图2 波峰模式检测示意图

图3 水平磁场变化示意图
波谷模式是利用垂直天线线圈所感应的垂直分量By,实现对管线的水平定位检测。当垂直线圈在管线上方横向移动时,会观测到线圈位于管线正上方感应电动势达到最小,此时为谷值;向两侧移动,感应电动势幅值逐渐增大,在左右两侧某个对称位置呈现峰值;继续移动,感应电动势逐渐减小,无穷远时衰减为零。图4及图5分别为波谷检测示意图及垂直磁场分量在不同埋深下变化示意图。

图4 波谷模式检测示意图
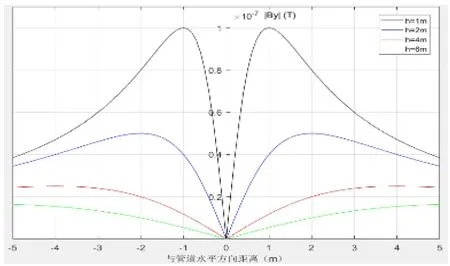
图5 水平磁场变化示意图
1.2 管线埋深检测方法
采用动态埋深计算方法对管线进行埋深检测。使用水平线圈对不同校准点进行信号值采集,并对应校准点深度值进行数据拟合,得到一条信号强度随管线埋深变化曲线。通过拟合曲线对其他位置信号值进行插值计算,并最终获取埋深数据[5-8]。采用logistc校准曲线函数模型对信号值与埋深值之间的函数关系进行曲线拟合,并得出信号值与管线埋深之间的关系表达式:
(4)
式中X为信号强度,h为管线埋深。
2 硬件电路设计
该文进行了管线探测仪硬件电路设计,并通过仿真及实验测试,验证了探测仪的性能。探测仪的功能是实现对接收天线所传入的信号,通过硬件与软件相结合的处理办法,将有用的信号信息提取出来,并通过相应算法,将信号信息转化为管线位置信息。系统由天线电路、50Hz工频噪声陷波模块、程控放大模块、选频滤波模块、AD采集模块、STM32单片机最小系统、按键模块、串口模块、LCD显示屏模块及电源模块构成。其结构图如图6所示。

图6 系统结构
通过按键,可对探测频率、放大倍数进行设定,并调整LCD显示模式。通过串口电路,可将采集到的信号数据传入上位机,在上位机中对软件滤波算法进行效果验证。
硬件电路对信号的处理分为预处理和数据采集及运算两部分。
预处理过程中,对天线传输来的信号进行陷波处理,以此消除市电干扰。对经过市电噪声滤除后的信号通过程控放大模块进行放大,使之达到AD采集芯片有效输入范围之内。再经过双T选频滤波电路,对信号进行选频,滤除带外噪声,最终将传输信号输入AD采集芯片。
数据采集及运算分为AD数据采集部分和单片机数据运算两部分。外部AD采集芯片将模拟信号转换为数字电平信号,并将转换得到的数字信号传送给单片机。单片机在接收到信号后进行计算拟合,得到有效的管线信息。
2.1 天线电路
接收天线依据电磁感应原理,通过其上的密绕线圈,将空间中的磁信号转化为天线系统的电压输入信号。输入信号经由程控选频电路,依靠其选频特性对信号带外噪声进行压制;程控选频部分为LC串联选频电路,密绕线圈可等效为电压源与自身电感的串联,并与电容、负载电阻共同构成LC串联选频电路。通过光电开关器件,单片机控制不同容值的电容接入电路,改变选频电路谐振点,实现对不同频率有效信号的带外噪声滤除。LC选频等效电路如图7所示。

图7 LC选频等效电路
图中L为线圈自身电感,r为线圈自身电阻,Cs为单片机选择连电容,Rs为后级等效负载电阻,l为电流流动方向。
2.2 50Hz陷波电路
电子器件的工作状态易受50Hz市电工频噪声的影响,其来源主要有两种。一种是从系统电源处引入,另一种则是空气中广泛存在电磁干扰。50Hz市电工频噪声幅值可远远大于有效信号,不对其进行专门的处理将会对后期的信号捕获带来困难,所以首先应用50Hz市电工频陷波电路对其进行滤除,再将处理后的信号送入后级电路。50Hz市电工频陷波电路采用F42N50集成陷波器及其外围电路构成。电路结构如图8所示。

图8 F42N50电路结构
由于50Hz噪声分量属于大噪声范围,其幅值Vnippmax>(VCC-VEE)/(2Q),所以选取RA和RG为82K,RQ为2K构成Q值为5的衰减单位增益型电路。信号由直流滤波电容C1传输进陷波电路中,最终经输出端滤直电容C2将信号传送给后级放大电路。对50Hz干扰进行陷波滤除后,信号增益空间得以释放,后级放大电路可有效实现对信号的放大功能。
2.3 程控放大电路
程控放大部分对经过市电噪声消除电路的输入信号进行放大及高频噪声的滤除。程控放大电路由两级运放构成,前级运放采用反向比例低通滤波放大电路。经前级运放的放大输出信号接入后级运放构成的电压跟随器,以此增大等效输入电阻,降低后级电路对程控放大电路的影响。图9为程控放大两级运放关系图。

图9 程控运放原理
图中ui为反向比例低通滤波器输入电压,即程控放大电路输入信号,经前级运放放大后输出电压为ud,ui与ud关系式为:
(4)

MC74HC4051芯片具有程控选通特性,将STM32主控芯片经由上拉电阻与MC74HC4051的A、B、C三脚相连,通过改变A、B、C引脚电平值,将X0~X7上连接的不同量值的反馈电阻Rf与匹配电容C1接入方向比例运算放大电路,实现对放大倍数的选择。图10为STM32芯片与MC74HC4051芯片的连接关系图。

图10 MC74HC4051与STM32连接图
其中X为MC74HC4051芯片输出通道,与X0~X7其中一脚形成通路。ENABLE脚为使能引脚,低电平芯片处于工作状态。
2.4 选频滤波电路
对放大后的信号进行带通选频滤波,滤除带外噪声,选用具有高选频特性的双T窄带选频带通滤波器,可大幅衰减无用噪声,提高信噪比。
选频滤波电路由两个独立运放搭建成两级电路,前级为双T选频电路,由运放A组成,实现对经由放大电路放大后的信号的选频滤波输出,后级为运放B构成的电压跟随器,实现对后级负载带来的影响的隔离。其电路结构如图11所示。
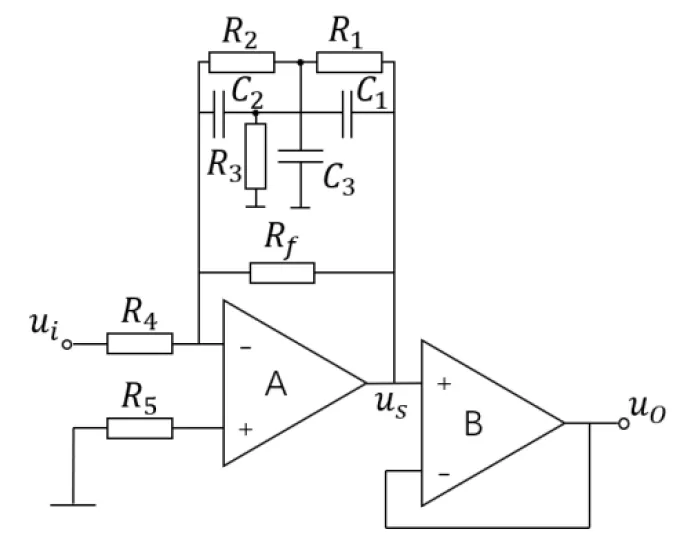
图11 选频滤波电路
双T选频电路是由双T带阻滤波器作为反馈网络,与反向比例运算放大器共同构成选频滤波放大电路,依据参考文献[9]中介绍的非对称系数选取方式,可实现高品质选频特性。双T选频电路是一种闭环负反馈系统[9]。
其系统闭环增益为:
(5)

(6)

(7)
其中:
(8)
(9)
上述公式中Q0为双T带阻滤波电路的品质因数,ω0为中心频率,α为不对称系数。
将公式带入闭环增益公式,可得以下公式:
(10)
式中:
(11)
Q为双T选频放大的品质因数,从上式可知,选频放大器品质因数Q不仅与α有关,而且与反向比例运算放大电路放大倍数AV有关,AV越大则Q值越大,选频放大器的选频特性也就越好。选取适当的α值和反向比例运算放大电路放大倍数AV可获得高效的选频特性。本系统采用Av绝对值为1,α值为3,从而实现对选频电路中的元件值的获取,并通过实验证明其具有高效的选频特性。
2.5 AD转换采集电路
AD采集电路将经预处理后的模拟信号转化为数字信号,并将其以二进制码的形式传送给单片机进行处理。
本设计采用AD7895ARZ-10型模数转换器。此款ADC芯片具有高速、12位高精度、±10V大幅值电压输入范围的性能,并具有片内时钟及高速串行接口,可实时得将转化得到的数字信号传送给处理器。AD7895ARZ-10由REFIN引脚读入模拟信号,并通过4个引脚与STM32的I/O相连,实现数字信号数据的传输。
图12为AD7895ARZ-10与STM32芯片连接示意图。
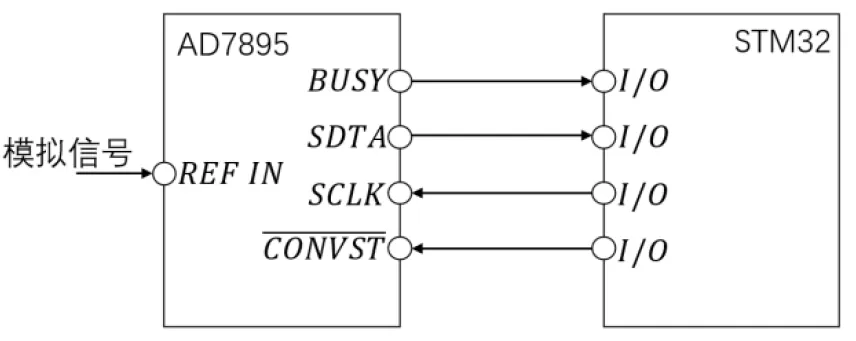
图12 AD7895与STM32连接
选用AD7895ARZ-10模式一进行数据采集,模式一为高速模式,平均采集频率最高可达192KHz,本系统使用的最高信号频率值为1KHz,所以满足奈奎斯特采样定律。
图13为AD7895ARZ-10模式一工作时序。

图13 AD7895ARZ-10模式一工作时序
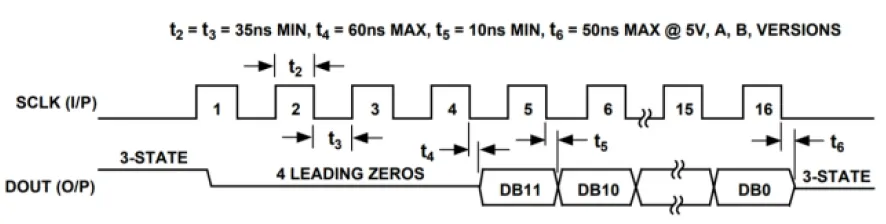
图14 串行数据传输时序
单片机I/O口与AD7895ARZ-10芯片SCLK引脚相连,为AD7895ARZ-10芯片提供串行时钟源,在每个SCLK的下降沿AD7895ARZ-10芯片从SDAT引脚输出一位数据。其中前4位为前导零值,后12位为AD转换数据的补码。单片机将接收到的补码装换成原码后存入数组,并依据对应AD采集频率转换成信号波形。
3 数字算法滤波
为得到有效的磁场感应电压信号,在硬件电路滤波基础上对经过AD转换得到的数字信号进行数字算法滤波处理可有效抑制干扰噪声对有用信号带来的影响。本系统采用FIR滤波器所构成的数字带通滤波器,对噪声有效滤除,从而获得较高的信噪比,进而通过有用信号获得管线位置信息。
设计具有与信号频率相同的中心频率的数字带通滤波器,在理论上可实现对带外噪声的有效滤除。采用有限长单位冲激响应(FIR)数字滤波器对理想带通滤波器进行逼近,可在实现有效逼近的同时,保证系统的因果稳定性及相位线性。
常用的FIR滤波器设计方法包括窗函数设计法、频率抽样法及最优化设计法等。在本设计中采用窗函数法对FIR滤波器进行设计[10]。
设理想带通滤波器系统函数为Hd(ejω),其时域内单位抽样响应函数为hd(n)。理想滤波器其单位抽样响应为无限长的非因果序列[11-13],所以理想的滤波器是不可实现的滤波器。采用窗函数对hd(n)进行N点的对称截取,对称中心为:
(12)
截取窗函数为:
w(n)n∈[0,1,…,N-1]
(13)
窗函数与理想滤波器的单位抽样函数相乘从而进行截取处理,加窗处理表达式如下:
h(n)=hd(n)W(n)
(14)
由上式可知,窗函数非零区间越长,所得到的h(n)越接近于理想滤波器的单位抽样响应函数hd(n),但依旧存在误差,此误差称为截取误差。
根据复卷积公式,时域相乘在频域则是周期性卷积,上式在频域内可等效为:
(15)
式中H(ejω)为h(n)对应的FIR滤波器系统函数,W(ejω)为窗函数频域变换函数。
采用不同类型窗函数对理想滤波器的逼近呈现不同效果,对逼近的好坏可用两种参数衡量,分别为过渡带宽度和阻带最小衰减。其中,过渡带宽度决定于W(ejω)主瓣宽度,控制主瓣宽度越窄,便可获得更陡峭的过渡带,从而逼近理想滤波器;阻带最小衰减决定于第一旁瓣相对幅度,第一旁瓣相对幅度越小,阻带最小衰减越强。上述两种要求不可能同时达到,通常以增加过渡带宽度换取效果更好的阻带最小衰减。表1为不同窗函数所具有的性能比较。

表1 不同窗函数性能参数
汉明窗相对于汉宁窗和布莱克曼窗,在窗的宽度相同时,旁瓣衰减和主瓣宽度适中,实际应用较为合适,因此本系统采用汉明窗对FIR滤波器进行设计。
设定带通滤波器中心频率为512Hz,窗函数长度为4个周期信号,在MATLAB中对窗函数进行滤波设计及仿真实验。将频率为512Hz,幅值为1的正弦信号作为有用信号,在其上叠加高斯白噪声,观察通过滤波器之后输出的波形,及输入输出信噪比,从而验证滤波器功能。图15为汉明窗的滤波效果图。
采用汉明窗进行滤波处理,其滤波前信噪比为-2.2448,滤波后信噪比为0.3890。
滤波前后信噪比增益有大幅度提高,且通过视觉观察可发现;滤波后输出波形与原始正弦信号接近程度非常高,从而可得,使用汉明窗所设计的FIR带通数字滤波器能有效滤除噪声并获得有用信号。
4 系统实际测试及功能验证
对地下管线进行实际探测,通过与同类型仪器RD4000进行同环境数据比较及开挖验证,以此验证系统性能。图16为RD4000。
使用本设计系统对20处数据采集点进行信号强度采集,并计算管线埋深,用RD4000采集数据进行对比。表2为各埋深数据采集计算值。

表2 不同埋深采集计算值
将本系统采集计算值与RD4000埋深探测数据进行图示数据对比,可得图17。

图17 埋深对比
由图17可直观看出本设计管线探测数据与RD4000探测数据相差较小,证明系统的实际可行性。对管线进行开挖验证,对采集点5点处开挖后管线实深6.46m。与多次本采集点测量值比较,最大误差为0.14m,最大误差比例为2.167%。验证系统精度较高,可用于实际探测。
5 结论
笔者基于电磁感应原理,设计了一款新型管线探测仪器。系统基于微弱信号检测相关理论,首先从硬件上对信号实现工频噪声滤除、放大、选频滤波和模数转换及采集功能,并在硬件信号处理的基础上实现单片机的FIR滤波器软件滤波,最终经由信号幅值与管线位置的对应拟合函数获得地下管线所处位置。
经实地测试,与同类产品RD4000进行实验比较,验证本系统对管线探测误差小,可以满足实际管线探测应用要求。
