基于Jenks算法粒度可控的微聚集数据扰动加密研究

钱小军

（江苏金盾检测技术有限公司，江苏 南京 210042）

0 引言

2019年以来，随着5G网络的蓬勃发展，整个人类社会进入了万物互联的时代[1]，从而在互联网中产生了海量的数据以及高并发的请求与响应[2-3]。因此，边缘计算的概念也逐渐进入了人们的视线。边缘计算，即为应用开发者和服务提供商在网络的边缘侧提供云服务和IT环境服务，目标是在靠近数据输入或用户的地方提供数据计算、存储的能力。在靠近数据输入或者用户的地方提供服务，避免了数据请求与响应在传输过程中的时延问题，分布式的计算服务环境也大大提高了数据计算效率。在移动终端日益增多、数据请求量日益扩大的情况下，边缘计算的出现弥补了解决传统云计算在这些方面的不足。然而，边缘计算也对用户的数据隐私保护带来了极大的挑战。

1 边缘计算架构

边缘计算架构如图1所示，可以看出，大多数用户终端的各项请求都交由距离其最近的一个或者多个边缘节点进行协同计算并返回，在此过程中边缘服务器与用户终端进行了数据交互。该过程虽然方便、快捷，但边缘计算各个节点的服务器往往不会像云服务器中心那样有较好的安全性，用户的数据隐私很容易泄露，因此，边缘计算中如何有效地保护用户的数据隐私成为一个热门话题。

图1 边缘计算架构

2 保护用户隐私的相关算法与技术

2.1 保护用户隐私问题的相关研究

目前，针对保护用户隐私问题的相关研究主要从隐私保护数据聚合、数据扰动和安全多方计算3个方面展开。

（1）隐私保护聚合主要是指每个本地设备从周围采集并加密数据，再将加密数据发送给边缘节点，边缘节点相互合作在密文数据上进行分布式的多方聚合计算，在必要的情况下将聚合结果发给云服务器做进一步的分析处理，或将聚合结果发送给授权接收方解密。

（2）数据扰动是指数据拥有者通过执行线性运算或非线性运算，以某些特定方式对原始数据进行盲化，然后将盲化后的数据外包给服务器用于数据分析与处理。

（3）安全多方计算是指在多用户间进行的安全计算的协议，其中，多个参与方共同对他们的输入数据进行计算，同时保持各个输入数据私有化。具体的隐私保护方案结构如图2所示。

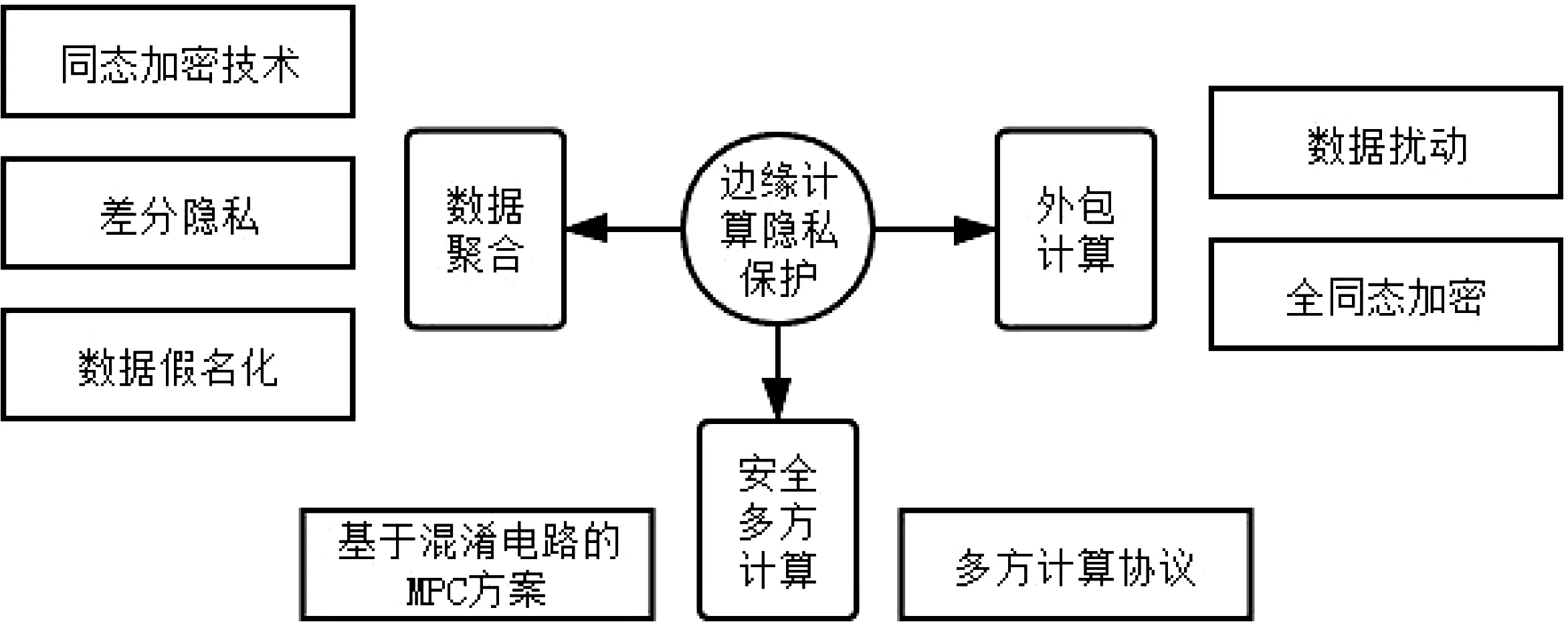
图2 边缘计算隐私保护概念

数据扰动作为隐私保护外包计算的关键技术，近年来有了长足的发展。数据扰动技术主要是进行数据扭曲与交换以及基于概率分布的扰动进行展开，其主要的扰动机制通常包括微聚集、添加噪声、加密以及多方计算等。数据扰动算法通过对用户端的原始数据进行随机扰动，对数据进行模糊化，隐藏了数据中的敏感信息。这个方法的好处是不用考虑攻击的类型与方式就可以很好地保证数据的隐私性，国内外的专家学者对此也有广泛的研究。

有学者提出了一种差分隐私保护模型，在数据上添加拉普拉斯噪声来对数据进行加密从而降低了隐私泄露的风险。Rahman等[4]认为，匿名认证的数据交换在不同的对等组织之间是必不可少的，并提出了一种基于配对密码的匿名动态安全数据交换协议，该协议允许云节点动态生成临时标识，用于为数据交换的每个会话生成会话密钥。虽然该方法不会改变原始数据的统计信息，但会造成后期数据挖掘的准确率大大降低。Lin等[5]提出了一种基于随机核矩阵的隐私保护内核k均值外包方法，该方法将数据向量进行扰动运算，在降低了数据隐私泄露的同时也降低了计算复杂度。另外，还有学者采用了概率扰动对数据进行隐私保护研究，虽然能够满足隐私保护的需要，但是算法只能针对单一数据，对于边缘计算中多类型的数据并不能提供很好的帮助。Mukherjees等[6]提出了一种基于傅里叶变换的数据扰动方法，利用傅立叶相关变换的能量压缩能力隐藏敏感数据值，以达到保护数据隐私的目的。

上述算法能够提高原始数据的隐秘性，但是其计算复杂度高，在追求快速响应的时代不能满足用户的需求，且在一定程度上改变了原始数据的分布，造成后期数据分析效率低下、准确率不高等问题。

2.2 基于Jenks自然断点算法的微聚集数据扰动算法

本文针对这一问题提出一种基于Jenks自然断点算法的微聚集数据扰动算法，能够有效地提高数据的安全性，实现数据的隐私保护与加密。微聚集算法是近年发展起来实现数据集k-匿名化的热点技术。

微聚集思想最早由Domingo等[7]提出，属于一种静态泄露技术，对原有数据进行失真处理。微聚集本质上是通过聚类后的子类中心点数值代替原数据，从而隐藏原数据，实现对隐私保护、数据加密方面的目标，微聚集的算法很多，但是通过微聚集实现对数据的扰动有两个必须满足的要求：（1）保持原数据的分布特性不能变，否则会影响到扰动后数据对于研究分析的利用；（2）要能达到对原数据加密的效果，实现数据隐私保护的目标。

微聚集的具体定义如下：给定数据表T(A1,A2,A3,…,An)，假设QI是T的准标识符，基于QI的一个k-划分将T划分为g个类，设Ci为第i类的类质心，对于所有i(i=1,…,g)，用Ci取代第i类中所有元素的操作称为聚集。其中准标识符（QI）是指能够以较高的概率结合一定的外部信息确定一条用户记录的数据。从k划分所依据的属性个数的角度, 微聚集算法可分为单变量微聚集算法和多变量微聚集算法两大类。遗传算法[8]和单轴[9]排序算法是单变量微聚集算法的两大主要方法，主要是根据准标识符的单个属性进行k划分操作；多变量微聚集算法以准标识符的多个属性为依据，以启发式的方式进行k划分[10-11]。微聚集在隐私保护中的应用也有了广泛的研究，如韩建民等[12]针对敏感值进行的微聚集研究、甘荣庆[13]针对隐私保护问题的微聚集研究、张刚景[14]针对多样性数据的微聚集研究等，这些研究证明通过微聚集算法可以很好地提高数据的隐私性，降低泄露的风险。

最优微聚集基于最优k划分[15]，要求划分后的类内同质性最大，好处是经过处理后的数据其信息的损失量最少。针对这一特性，本文引入Jenks自然断点算法作为本文的微聚集算法。对于Jenks自然断点算法，该算法秉承的是分段后“组内间距最小，组间距离最大”这一思想，这与最优微聚集的思想基本一致，是基于数据中固有的自然分组对分类间隔加以识别，对相似值进行分组，使各类元素间的差异最大化。Jenks自然断点算法认为，任何数列之间，都存在一些自然（非人为设定的）的转折点和断点，这些自然的断点都是具有统计学意义的，用这些转折点可以把研究的对象分成性质相似的群组，因此自然断点本身就是分级的良好界限。其计算方法为：

式中：SSD表示方差；i、j表示第i、j个元素；A表示长度为N的数组；k表示i、j中间的数，表示A组中的第k个元素。

3 基于Jenks算法粒度可控的微聚集数据扰动加密算法

3.1 最强影响边缘点求解步骤

求解最强影响边缘点的第一步就是求解边缘点。边缘点就是距离其所属子类中心点最远距离的点。

本文提出的边缘点的求解算法如下：（1）设原始数据集经过Jenks自然断点算法后将原始数据集划分为m类，子类C为其中一类；设数据X∈C且数据维度为n维，即X=＜X1,X2,X3,…,Xn＞；（2）按照X1维度对子C类中所有数据进行降序或者升序排序（两个排序方式皆可，但在算法中需要统一，即要么全部按照升序排序，要么全部按照降序排序）；（3）遍历按照X1维度数据大小排序后的数据集，按照X2维数据大小展开降序或者排序操作，排序规则同上一步骤；（4）以此类推，直至按照第Xn维度的数据大小排序完成；（5）从Xn维开始，位于每一维最大值的2个点放入边缘点集合。

经过上述求解算法，可以求得每个子类中的两个距离子类中心最远的边缘点，从而生成了边缘点集合。由于Jenks自然断点算法的特性，其类内数据间隔是最小的，而类与类之间的间隔是比较大的，我们假设边缘点d1和d2分属于不同的两个子类C1、C2，且C1、C2为相邻的两个子类，根据Jenks自然断点算法的思想，两个相邻的子类中距离最近的一对数据点一定位于各自子类的边缘区域（即上述算法所求的边缘点），并且这两个点对于Jenks算法分类的结果影响最大，在本文中称为最强影响边缘点。求解两个子类中一对最强边缘点的算法流程如下：

（1）设集合A和集合B分别为子类C1和C2的边缘点集合，即A∈C1、B∈C2，且A∩B=∅；

（2）遍历计算集合A和集合B中所有数据点间的距离di,j，di,j的计算方法为：

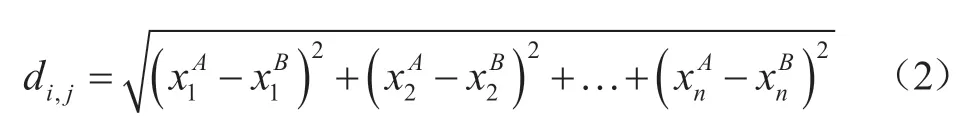
（3）取使得距离di,j最小的两个边缘点的坐标，即为一对最强影响边缘点。

3.2 粒度可控的微聚集扰动算法

经过上文最强影响边缘点的求解后，可以得到数据集中各个子类之间的一对最强影响边缘点，该组边缘点对于基于Jenks自然断点算法的数据分类结果有着非常大的影响，对其进行进一步的操作以实现粒度可控的微聚集数据扰动算法，从而降低数据安全性、降低数据泄露的风险。

该算法的主要步骤：（1）根据实际情况需要以及隐私保护的目标，预先设定Jenks自然断点算法的子类数目以及加密后预期的子类数目，分别记为和。显然，加密后的子类数目明显小于预先设定的子类数目；（2）根据预设子类数目执行Jenks自然断点算法，得到分类后的数据集；（3）根据3.1小结中提出的算法，分别求出两两子类之间距离最近的边缘点，作为一组最强影响边缘点对，并按照边缘点对中两个点的距离从小到大排序；（4）进入循环迭代环节，具体如下：

如果：当前聚类数目达到加密预期的子类数目，则算法结束，并返回各子类中心点作为解密结果。

否则：第一，找到距离最近的最强影响边缘点对；第二，取这一对数据距离的中心点生成新的数据添加到数据集；第三，从数据集中删除这一对最强影响边缘点；第四，再执行Jenks聚类算法以及最强影响边缘点对求解算法；第五，返回第一步。

在上述算法中，每执行一次即删除一对最强影响边缘点，同时新增一个点，这个新增的点即成为原先二个不同子类的连接点，从而影响下一步Jenks聚类算法的分类结果，对原先的数据集产生扰动，该操作不会给原始数据带来过多的数据噪声，在提高了数据安全性的同时也保证了数据的原始特征，为后续的数据计算降低了误差。

4 结语

随着5G网络和边缘计算的发展，如何保证用户的数据隐私已经变得越来越重要。保护数据隐私的要求非常高：（1）要有效地对用户原始数据进行保护；（2）对原始数据进行的相关操作不能太过复杂，才能保证请求的快速响应；（3）要尽可能降低对于原始数据特征的影响，保证数据的原始性，才能为后续的数据计算等一系列操作带来可能。本文针对现有问题以及隐私保护的需求，提出了一种基于Jenks自然断点算法对原始数据进行微聚集的方法，实现了对原始数据的隐私保护与加密，并通过最强影响边缘点的删除与新增子类联接点，实现了对聚类的结果进行修订，从而进一步增强算法对数据的扰动作用。

由于本文算法利用了Jenks算法的特点，即可以预设原始数据的聚类子类数目，再通过最强影响边缘点的修改逐步有目标地调整数据扰动的效果，实现了粒度可控的微聚集数据扰动加密算法。该算法满足了数据扰动的需求，同时由于变化的是最强影响边缘点，对于数据集的整体扰动不大，对于数据集统计特征影响有限。不足的是，本文算法中求解边缘点的算法只适应于凸数据集，后期可以进一步研究相关算法使之适应于各类数据集。