基于R2 指标和参考向量的高维多目标进化算法
2022-01-09陈国玉李军华黎明陈昊
陈国玉 李军华 黎明 陈昊
多目标优化问题(Multi-objective optimization problems,MOPs)[1]是指多个目标被同时优化的问题.在现实生活中,经常遇到优化问题包含四个及以上目标,这类问题统称为高维多目标优化问题(Many-objective optimization problems,MaOPs)[2−4].虽然一些经典的多目标进化算法(Multi-objective evolutionary algorithms,MOEAs),NSGA-II[5]、SPEA2[6]等能够很好地处理多目标优化问题(两个或三个目标),但是在解决高维多目标优化问题上效果较差.
近年来,为了提高解决高维多目标优化问题的能力,研究者们提出了许多优秀的算法,这些MOEAs 主要可以分为三类.1) 基于各种增强收敛性的算法:该类算法主要是改进Pareto 支配关系或者提出其他增强收敛性的方法,通过这些方法提高处理高维多目标优化问题时的收敛性.例如改进的Pareto 支配:∊支配[7]、L 最优[8]、模糊支配[9]和优先级排序[10]等.以及其他基于增强收敛性的算法:GrEA[11]、KnEA[12]等.2) 基于分解的算法:该类算法是把一个复杂的高维多目标优化问题分解为一组单目标优化问题(Single-objective optimization problems,SOPs) 或者易于管理的多目标优化问题[13−15],如RVEA[16]、SPEA/R[17]和NSGAIII[18]等.3) 基于评价指标的算法:该类算法是采用评价指标作为选择标准来衡量解的质量,选择机制通过比较解的质量找到更好的解.这类算法的典型代表包括IBEA[19]、HypE[20]和SMS-EMOA[21]等.
虽然大多数多目标进化算法能够很好地处理一些高维多目标优化问题,但这些算法对Pareto 前沿的形状十分敏感[22],导致在处理不同形状的PF 时不能很好地平衡收敛性和多样性.针对上述问题,本文提出了一个基于R2 指标和参考向量的高维多目标进化算法(R2-RVEA).该算法的主要创新在于:1) R2-RVEA 基于Pareto 支配作为选择标准选取非支配解,仅当非支配解的数目超过种群规模时,算法进一步采用R2 指标选择和种群分解策略共同管理多样性;2) R2-RVEA 基于R2 指标进一步选择种群分解淘汰的解,这有利于保留具有良好收敛性和多样性的解.
1 相关工作
1.1 基于指标的多目标进化算法
目前,相关文献提出了许多评价指标,有衡量收敛性的评价指标:世代距离(GD)[23];衡量多样性的评价指标:PD[24];同时衡量收敛性和多样性的评价指标:反世代距离(IGD)[25]、超体积(HV)[26]、R2[27]以及IGD-NS[28].这些指标广泛的应用于评估解集的质量,有些指标还被用作MOEAs 的选择标准.
基于评价指标的MOEAs 比较典型的算法有:IBEA[19]、HypE[20]、SMS-EMOA[21].Zitzler 等在2004 年提出IBEA[19],该算法首先用二进制评价指标来定义优化目标,然后使用它作为选择标准.通过几个MOPs 测试问题的实验,结果表明IBEA 的性能优于NSGA-II[5]和SPEA2[6].同时,IBEA 的主要贡献是为基于评价指标的MOEAs 提供了一个通用框架,它可以嵌入其他评价指标设计算法.
SMS-EMOA[21]是由Beume 等提出的基于评价指标的MOEAs.该算法采用了HV 指标作为选择标准,通过实验对比,可以看出SMS-EMOA 能够很好地处理多目标优化问题,但是在处理高维多目标优化问题时,HV 的计算成本会随着目标数目的增加呈指数型增加.针对这个问题,Bader 和Zitzler 提出了一种基于快速HV 的进化算法用于高维多目标优化(HypE)[20].在HypE 中,为了减少HV 计算成本的消耗采用Monte Carlo 估计法进行估计近似的HV 值而不是计算精确的HV 值,这使得HV 的计算效率在目标数很大时明显提高.
近年来,陆续出现了一些基于指标的MOEAs,例如:Tian 等[29]提出了一种基于指标的MOEAs(AR-MOEA),该算法采用了IGD-NS 指标作为选择标准,并且设计了一种参考点适应方法调整参考点来处理不同形状的PF;还有Sun 等提出的一种基于IGD 指标的进化算法(MaOEA/IGD)[30],该算法采用了IGD 指标挑选出收敛性和多样性良好的解,并且利用计算效率较高的支配表方法来分配解的等级值.
最近的一些研究表明R2 指标能够很好地平衡收敛性和多样性.R2-IBEA[31]消除了选择中的支配排序,利用R2 指标作为选择标准进行个体选择.通过实验表明,该算法能够在空间中产生分布较好的个体.Trautmann 等提出了一个基于R2 指标选择的多目标搜索算法(R2-EMOA)[32],该算法首先采用非支配排序管理种群,而R2 指标作为第二选择标准管理非支配排序的临界层.此外,MOMBIII[33]通过采用成就量化函数(ASF) 替代加权切比雪夫度量以处理高维多目标优化问题,并提出一种参考点更新方法来解决归一化过程中解集的多样性对选择参考点敏感的问题.通过与多个算法大量的对比实验表明,MOMBI-II 能够很好地处理超多目标优化问题.近期,Li 等提出了一个基于两阶段R2指标的高维多目标进化算法(TS-R2EA)[34],首先采用R2 指标作为主要选择方法,参考向量引导的目标空间划分方法则作为第二选择策略.这些基于R2指标的算法在处理MOPs 和MaOPs 上都展现了良好的性能,此外,R2 指标低计算复杂度和弱支配兼容性的特性非常适合作为选择标准应用到算法中.
1.2 基于分解的多目标进化算法
MOEA/D[13]是基于分解的MOEAs 的代表性算法,它设置了一组均匀分布的权重向量,将高维多目标优化问题分解为一组子问题,而每个子问题的优化都是使用其相邻子问题的当前信息.此外,在RVEA[16]中,它采用一组均匀分布的参考向量,把高维多目标优化问题分解为一组单目标问题(SOPs),使得候选解收敛到每个单目标问题的最优情况,而无需考虑不同目标之间的冲突,通过大量实验证明,RVEA 能够很好地处理高维多目标优化问题.
基于分解的多目标进化算法基本上采用参考点、参考向量以及权重向量等分解目标空间,由于它们作用相同,本文统一定义为参考向量.Das 和Dennis 提出的系统化方法[35]是一种广泛使用的参考向量生成方法,该方法把点放在标准化的超平面上(一个(M −1)维的单元网格) 倾向于所有目标轴并且在每个坐标轴上都有一个截距.如果每个目标都考虑到p个网格,则一个M目标上总数为N的参考向量为:

例如在一个3 目标(M=3)问题上,考虑到每个目标有4 个网格(p=4),则生成总数为15 的参考向量如图1 所示.
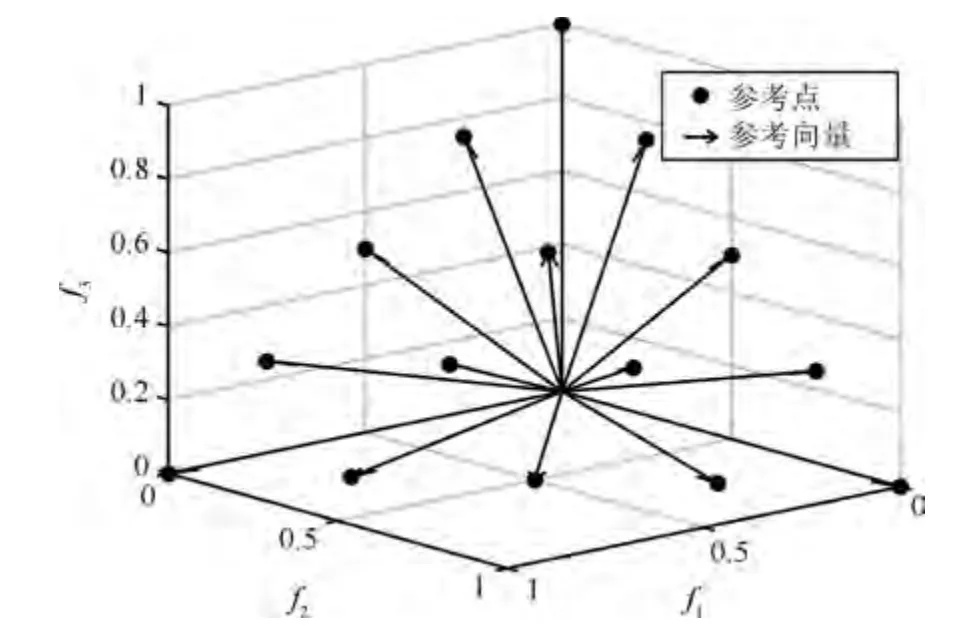
图1 目标问题上展示的15 个参考向量Fig.1 15 reference vectors are shown on 3-objective problem
2 基于R2 指标和参考向量的高维多目标进化算法
2.1 基于分解的多目标进化算法
R2-RVEA 采用Pareto 支配作为选择标准,选取非支配解指导种群进化,当非支配解的数目超过种群规模时,算法进一步采用种群分解策略和R2 排序选择管理多样性.由于很多时候种群分解选取解的数目无法满足种群规模,利用R2 排序能够从种群分解淘汰的解中保留收敛性和多样性较好的解来进一步满足种群规模.如算法1 所示,R2-RVEA 的主要框架包含了下面的步骤:首先,初始生成一个规模为N的种群,以及一个均匀分布的参考向量集合V规模为N;然后,在主循环中,子代Qt由父代Pt随机生成,合并到父代种群Pt中进入环境选择;最后,执行环境选择从合并种群中挑选出N个候选解进入下一代.在下面会着重介绍三个子部分,分别是环境选择、种群分解和R2 排序.
算法1.R2-RVEA 算法框架


2.2 环境选择
如算法2 所示,环境选择的最初阶段只采用非支配排序获得当前种群的非支配解集合At,如果At中解的数目小于等于种群规模N,At就会作为种群Pt+1进入下一代,这使得种群可以快速地收敛到PF 上,并且避免较差解误导种群进化方向.
算法2.环境选择

i ∈{1,···,M},分别表示第i个解的标准化前和标准化后的目标值.
2.3 种群分解
种群分解选择过程如算法3 所示.首先,通过将每个解与最近的参考向量联系起来,把种群At分解为一组子种群.角度可以衡量解和参考向量之间的空间关系,如果一个解和参考向量之间的角度最小,那么就会被分配到这个参考向量所代表的子种群中.
算法3.种群分解

经过种群分解以后,适应度值将作为每个子种群内的选择标准进行精英选择,适应度值计算公式如下:
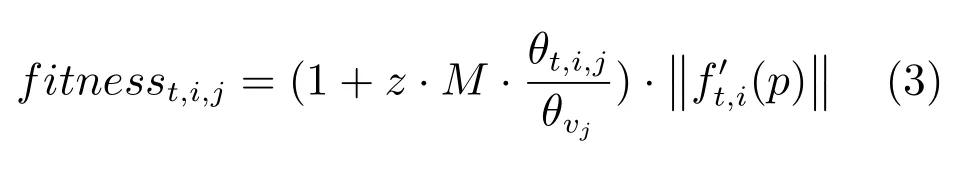

适应度计算同时衡量了解的多样性和收敛性,利用对解与向量的夹角进行标准化,角度标准化过程使得适应度值对解和向量之间的夹角变得敏感,采用z是考虑了在不同目标存在不同量化范围的情况,这就可以使适应度值计算对多样性敏感,能够有益于解的选择.在每个子种群中,适应度值最小的解会被选作是精英进入下一代,组成解集合
2.4 R2 排序
R2 指标可以用来评估两个集合的相关质量,分别由一个给定的近似集合A、一组权重向量WWW以及效用函数构成,R2 指标定义如下:

i=1,···,N,WWW=(w1,w2,···,wn) 是权重向量.关于等级的正式定义源于式(5),提出如下等式:
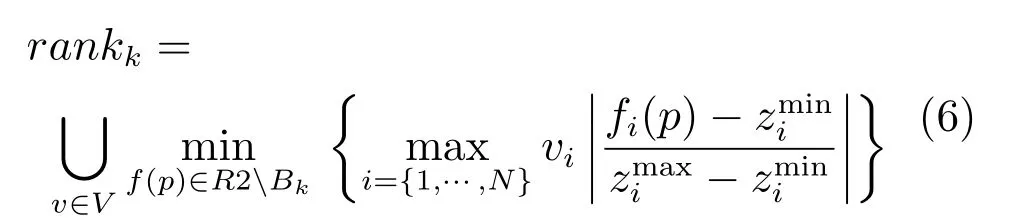
Bk=是最低等级解的集合.而当两个解的效用值相同时,其中具有较低欧氏距离的解将会被选出,这能够有效地消除松弛的Pareto 解.
在R2-RVEA 中,选择ASF 作为R2 排序的效用函数.首先,利用式(6) 计算所有解的函数值,获得能够优化效用函数的解,将这些解放在顶层,这样就获得了第一等级(最优等级);然后,移除第一等级的解,以同样的方式识别剩下的解,获得第二等级;整个排序过程将一直持续,直到所有的解都被排序.R2 排序过程在算法4 中给出.种群分解淘汰的解通过R2 排序以后,从排序后的集合中选出前k个最好的解组成集合Rt.
算法4.R2 排序


3 实验仿真及分析
在这个部分,提出的算法主要和当前较好的6 个MOEAs 进行实验对比,分别是NSGAIII[18]、RVEA[16]MOEA/DD[36]、MOMBI-II[33]、KnEA[12]和TS-R2EA[34],实验取自DTLZ 测试集和WFG 测试集.首先,进行实验设置;然后,DTLZ 测试集中各个测试问题的实验结果和对比分析;接下来,WFG 整个测试集的实验结果以及对比分析;最后,算法性能分析.
在实验中,采用了DTLZ[37]测试集中的测试问题DTLZ1-DTLZ7 以及WFG[38]测试集中的测试问题WFG1-WFG9.在DTLZ 的一个给定的M目标测试问题中,每一个目标函数都有n=k+M −1个决策变量,在DTLZ1 中k设置为5,DTLZ2-DTLZ6 中k设置为10,以及在DTLZ7 中k设置为20.此外,WFG 基准测试套件中每一个给定测试问题的每个目标函数都有n=k+l个决策变量,k设置为(M −1) 以及l设置为10.本文算法基于MATLAB2016a 实现,并采用多目标进化算法平台PlatEMO[39]进行算法对比.
3.1 实验设置
1) 交叉和变异算子设置:采用传统的二进制交叉[40]和多项式变异[41]适用于所有的多目标进化算法.在本文中,交叉概率和变异概率分别设置为1.0 和1/n(n代表决策变量数目).而SBX 和多项式变异的分布指标都设置为20.
2) 种群规模:R2-RVEA、NSGA-III[18]、RVEA[16]、MOEA/DD[36]、MOMBI-II[33]、KnEA[12]和TS-R2EA[34]的种群规模取决于参考向量的数量.而这些参考向量采用单网格设计系统[18]生成.为了对比的公平,KnEA[12]设置与其他算法相同的种群规模.详细配置列在表1 中.

表1 种群规模设置Table 1 Setting of population size
3) 终止条件:每一次运行的终止条件是最大代数.对于所有测试问题,在不同目标上的最大代数设置不同.在3 目标和5 目标的最大代数设置为1000,在10 目标上设置为1300,而15 目标的最大代数设置为1500.
4) 评价指标:算法的性能由HV[23]指标和IGD+[42]指标来评估.在计算HV 之前,所有目标值都要通过PF 值进行标准化.然后,HV 值就利用参考点(1,1,···,1) 和标准化后的目标值计算得来.此外,一旦目标数目大于等于5,Monte Carlo[20]评估方式采用1000000 个样点进行更有效的计算.在IGD+指标计算中,对于每个测试实例,利用Das 和Dennis 方法在PF 上采样大约5000 个均匀分布的点.此外,对于10 目标和15 目标问题,则采用双层Das 和Dennis 方法生成采样点.
5) 统计方法:每个算法在每个测试问题上都独立运行30 次,然后采用Wilcoxon 秩和检验方法比较R2-RVEA 与其他对比算法获得的结果,其中均值分析的显著性水平设置为0.05.根据Wilcoxon 秩和检验方法,‘+’表示对比算法要优于R2-RVEA,‘−’表示对比算法获得的结果比R2-RVEA 的结果差,‘≈’表示对比算法和R2-RVEA 获得的结果没有明显的差异.
6) 对比算法参数设置:对于RVEA 和TSR2EA,在对比实验中频率参数fr和指标α分别设置为2 和0.1.在MOEA/DD 中,邻域规模T和惩罚参数θ分别设置为20 和5,临近选择概率设置为δ=0.9.对于MOMBI-II,差异门限α,公差门限∊和最小向量的记录规格分别设置为0.5,0.001 和5.KnEA 的参数设置参考文献[12].
3.2 算法在DTLZ1-DTLZ7 上对比分析
该节给出了7 个算法在DTLZ 测试集上的实验结果,表2 和表3 分别汇总了对比算法所获得的HV 值和IGD+值的均值和标准差(括号内为标准差).其中,突出最好的结果.
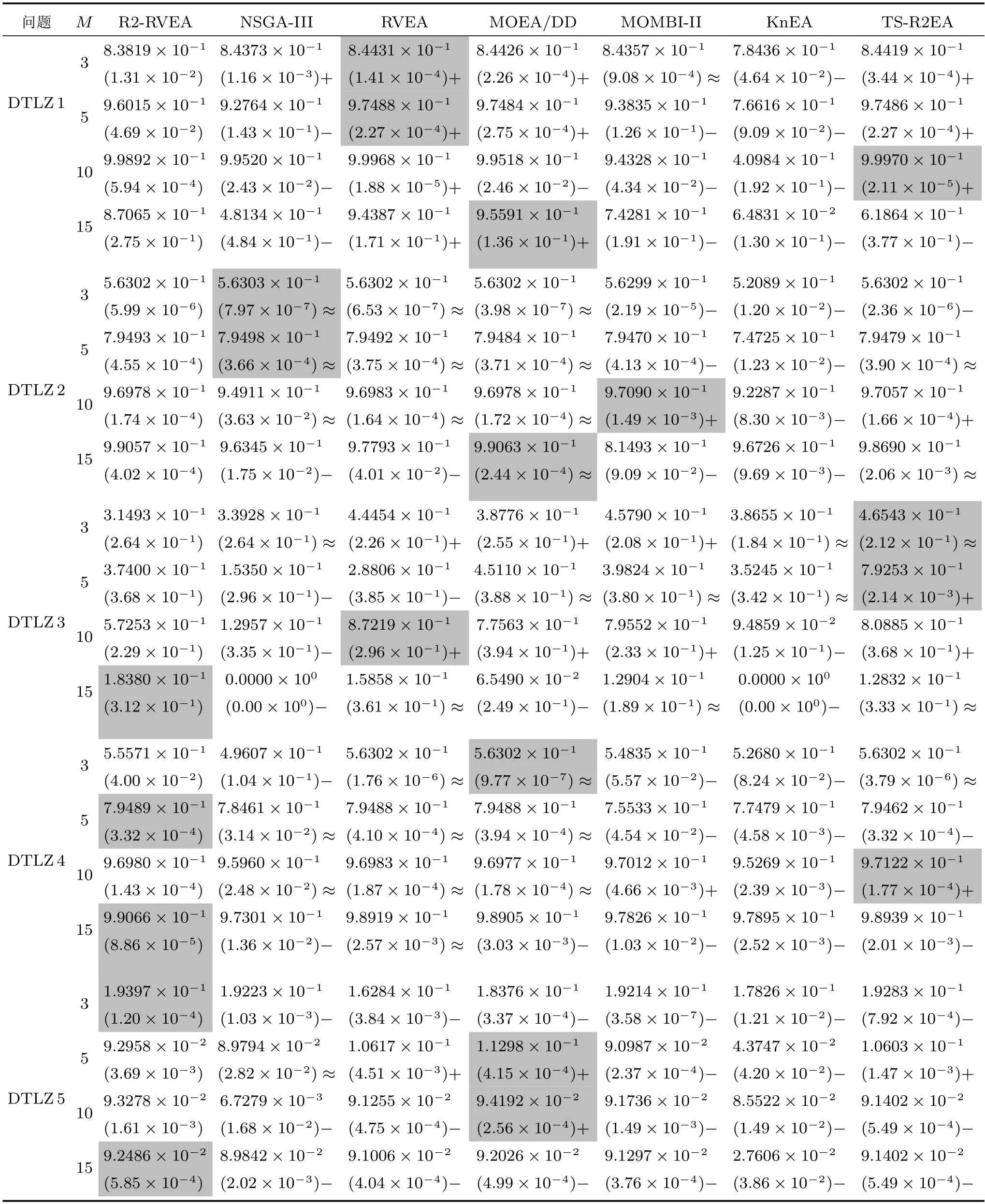
表2 R2-RVEA、NSGA-III、RVEA、MOEA/DD、MOMBI-II、KnEA 和TS-R2EA 在DTLZ1−DTLZ7 上获得的HV 值的统计结果(均值和标准差).最好的结果已突出Table 2 The statistical results (mean and standard deviation) of the HV values obtained by R2-RVEA,NSGA-III,RVEA,MOEA/DD,MOMBI-II,KnEA and TS-R2EA on DTLZ1 to DTLZ7.The best results are highlighted
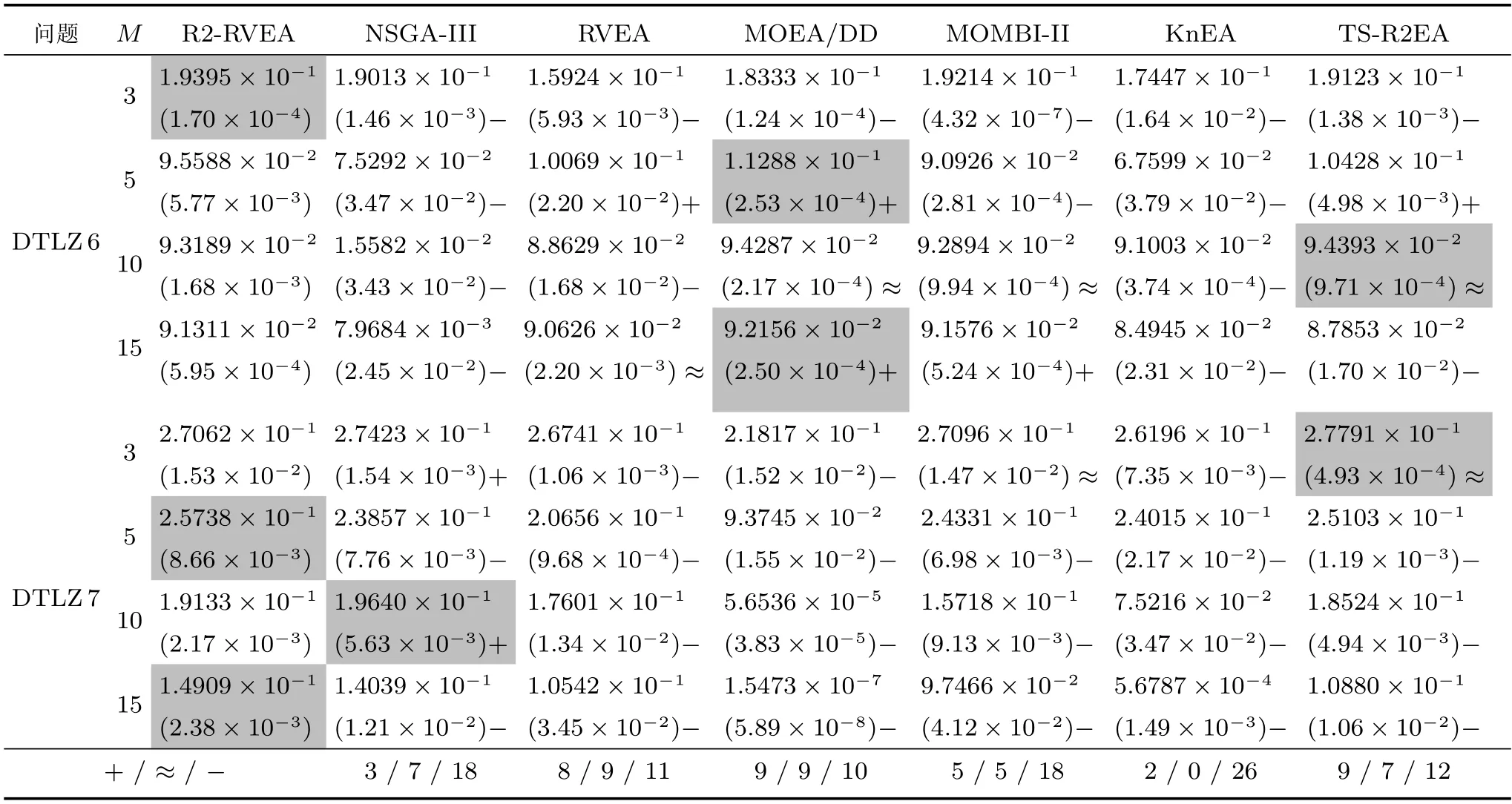
表2 R2-RVEA、NSGA-III、RVEA、MOEA/DD、MOMBI-II、KnEA 和TS-R2EA 在DTLZ1−DTLZ7 上获得的HV 值的统计结果(均值和标准差).最好的结果已突出(续表)Table 2 The statistical results (mean and standard deviation) of the HV values obtained by R2-RVEA,NSGA-III,RVEA,MOEA/DD,MOMBI-II,KnEA and TS-R2EA on DTLZ1 to DTLZ7.The best results are highlighted(Continued table)

表3 R2-RVEA、NSGA-III、RVEA、MOEA/DD、MOMBI-II、KnEA 和TS-R2EA 在DTLZ1 DTLZ7 上获得的IGD+值的统计结果(均值和标准差).最好的结果已突出Table 3 The statistical results (mean and standard deviation) of the IGD+values obtained by R2-RVEA,NSGA-III,RVEA,MOEA/DD,MOMBI-II,KnEA and TS-R2EA on DTLZ1 to DTLZ7.The best results are highlighted

表3 R2-RVEA、NSGA-III、RVEA、MOEA/DD、MOMBI-II、KnEA 和TS-R2EA 在DTLZ1 DTLZ7 上获得的IGD+值的统计结果(均值和标准差).最好的结果已突出(续表)Table 3 The statistical results (mean and standard deviation) of the IGD+values obtained by R2-RVEA,NSGA-III,RVEA,MOEA/DD,MOMBI-II,KnEA and TS-R2EA on DTLZ1 to DTLZ7.The best results are highlighted(Continued table)
综合HV 和IGD+的统计数据分析结果.DTLZ1-DTLZ4 具有规则形状的PF,虽然R2-RVEA 没有在所有测试实例中获得最具竞争力的性能,但总体上获得了良好的性能,由图2 可以看到各个算法获得的非支配解在DTLZ4 上15 目标实例中的分布情况.DTLZ5-DTLZ7 具有不规则形状的PF,对于DTLZ5 和DTLZ6,R2-RVEA 主要在DTLZ5 的3 目标和DTLZ6 的3 目标上获得了最好的性能,而在其他目标上的最好性能主要由MOEA/DD 获得,由图3 中可以看到各个算法获得的非支配解在DTLZ5 上3 目标实例中的分布情况.在DTLZ7 上,综合两个指标的统计数据得出R2-RVEA 获得了一般的性能,NSGA-III 性能相对稳定,总体性能相对较好,图4 是各个算法获得的非支配解在DTLZ7 上5 目标实例中的分布情况.综合统计结果可以看出,R2-RVEA 在DTLZ 测试集上虽然没有在每个测试实例上获得最优的结果,但总体性能良好.

图2 DTLZ4 问题15 目标上获得的非支配解Fig.2 Nondominated solutions obtained on 15-objective DTLZ4
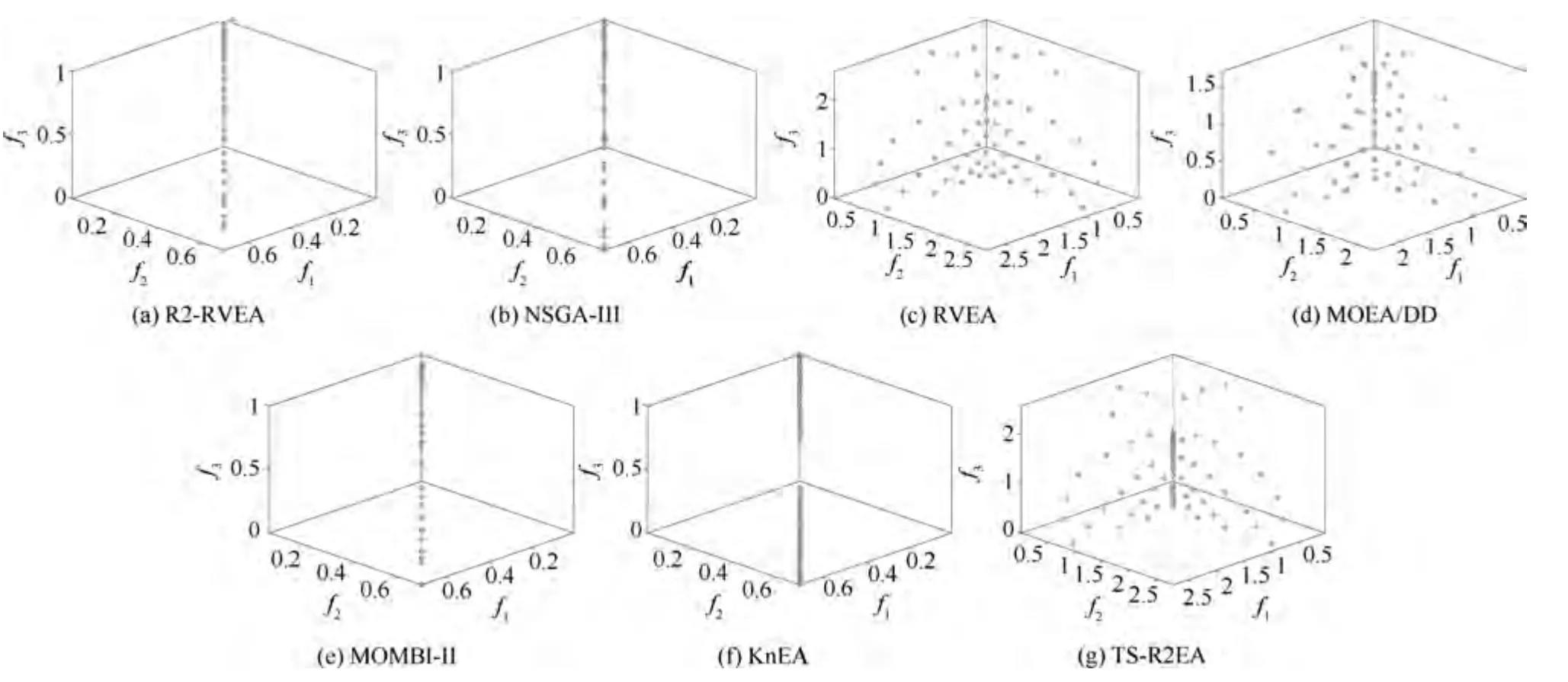
图3 DTLZ5 问题3 目标上获得的非支配解Fig.3 Nondominated solutions obtained on 3-objective DTLZ5

图4 DTLZ7 问题5 目标上获得的非支配解Fig.4 Nondominated solutions obtained on 5-objective DTLZ7
3.3 算法在WFG1-WFG9 上对比分析
该节给出了7 个算法在WFG 测试集上的实验结果,表4 和表5 分别汇总了对比算法所获得的HV 值和IGD+值的均值和标准差(括号内为标准差).其中,突出最好的结果.
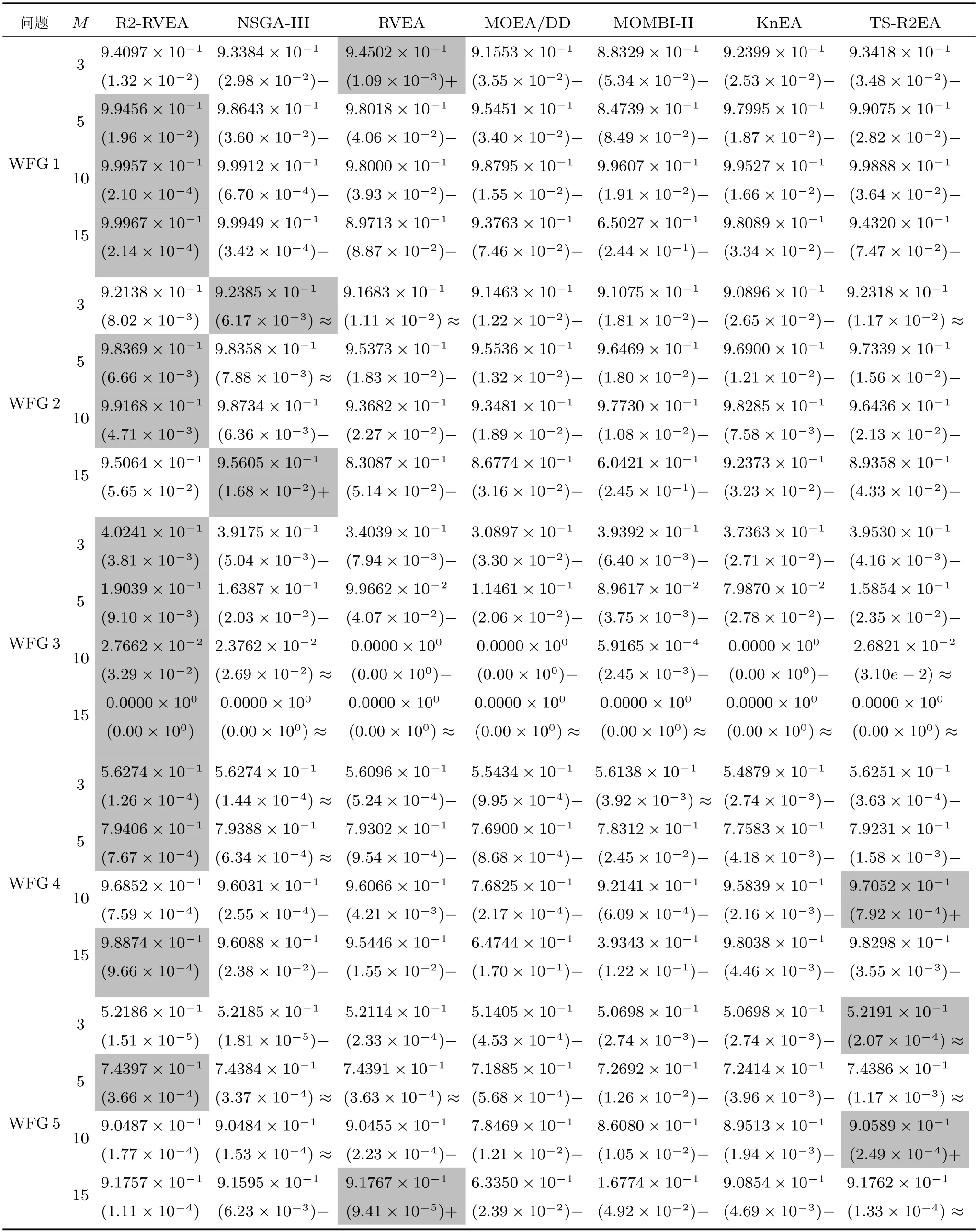
表4 R2-RVEA、NSGA-III、RVEA、MOEA/DD、MOMBI-II、KnEA 和TS-R2EA 在WFG1-WFG9 上获得的HV 值的统计结果(均值和标准差).最好的结果已突出Table 4 The statistical results (mean and standard deviation) of the HV values obtained by R2-RVEA,NSGA-III,RVEA,MOEA/DD,MOMBI-II,KnEA and TS-R2EA on WFG1 to WFG9.The best results are highlighted

表4 R2-RVEA、NSGA-III、RVEA、MOEA/DD、MOMBI-II、KnEA 和TS-R2EA 在WFG1-WFG9 上获得的HV 值的统计结果(均值和标准差).最好的结果已突出(续表)Table 4 The statistical results (mean and standard deviation) of the HV values obtained by R2-RVEA,NSGA-III,RVEA,MOEA/DD,MOMBI-II,KnEA and TS-R2EA on WFG1 to WFG9.The best results are highlighted(Continued table)

表5 R2-RVEA、NSGA-III、RVEA、MOEA/DD、MOMBI-II、KnEA 和TS-R2EA 在WFG1-WFG9 上获得的HV 值的统计结果(均值和标准差).最好的结果已突出Table 5 The statistical results (mean and standard deviation) of the IGD+values obtained by R2-RVEA,NSGA-III,RVEA,MOEA/DD,MOMBI-II,KnEA and TS-R2EA on WFG1 to WFG9.The best results are highlighted
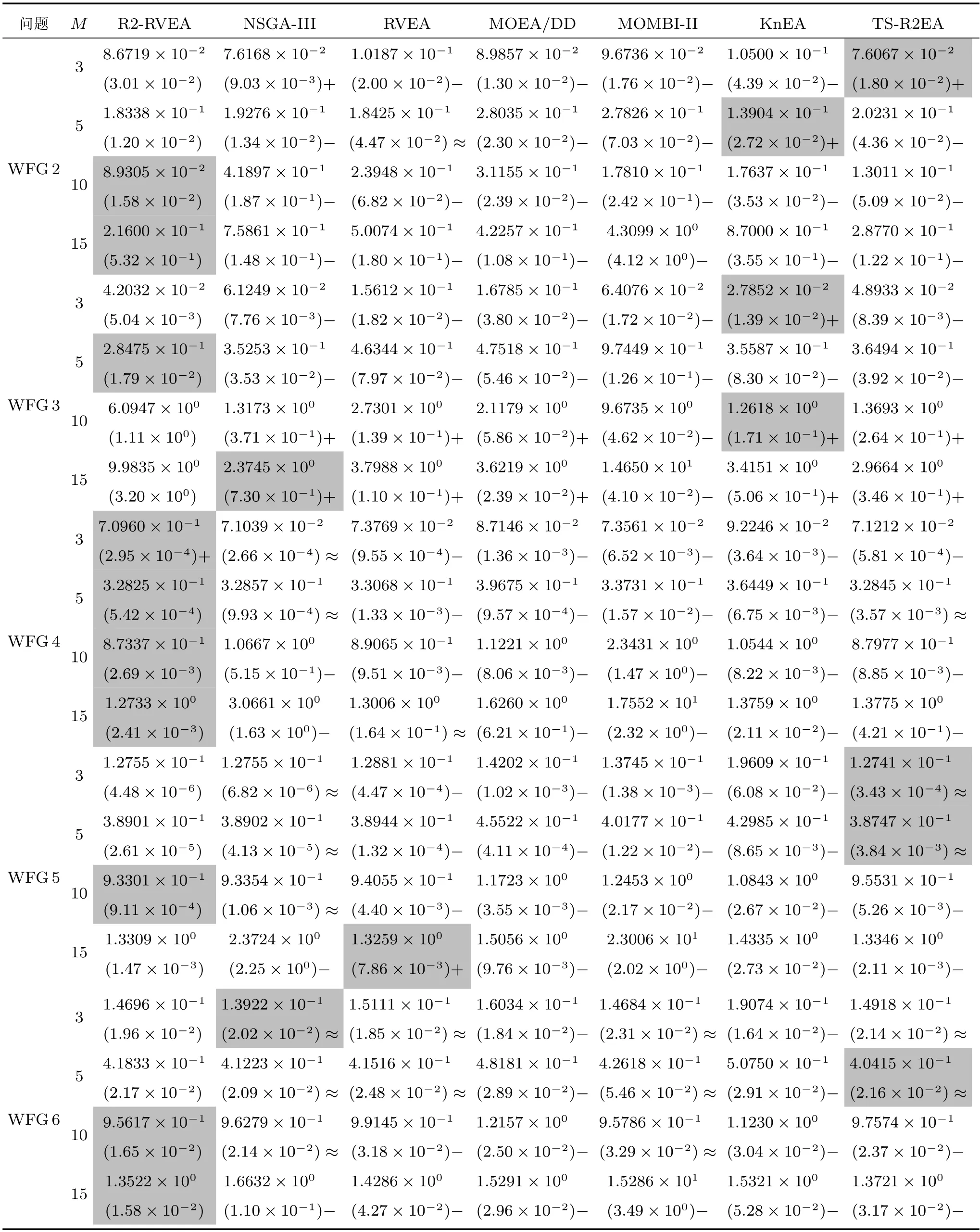
表5 R2-RVEA、NSGA-III、RVEA、MOEA/DD、MOMBI-II、KnEA 和TS-R2EA 在WFG1-WFG9 上获得的HV 值的统计结果(均值和标准差).最好的结果已突出(续表)Table 5 The statistical results (mean and standard deviation) of the IGD+values obtained by R2-RVEA,NSGA-III,RVEA,MOEA/DD,MOMBI-II,KnEA and TS-R2EA on WFG1 to WFG9.The best results are highlighted(Continued table)
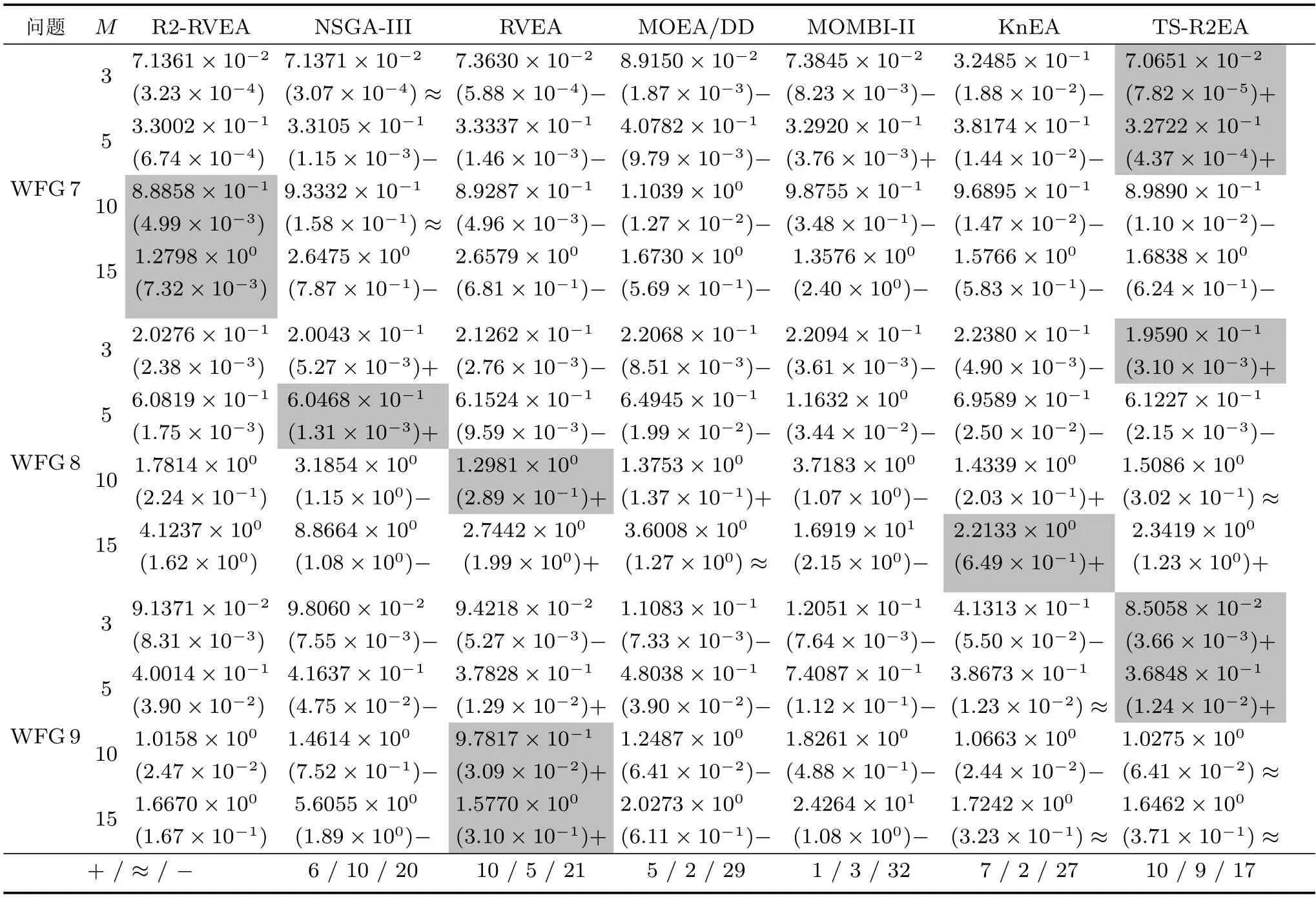
表5 R2-RVEA、NSGA-III、RVEA、MOEA/DD、MOMBI-II、KnEA 和TS-R2EA 在WFG1-WFG9 上获得的HV 值的统计结果(均值和标准差).最好的结果已突出(续表)Table 5 The statistical results (mean and standard deviation) of the IGD+values obtained by R2-RVEA,NSGA-III,RVEA,MOEA/DD,MOMBI-II,KnEA and TS-R2EA on WFG1 to WFG9.The best results are highlighted(Continued table)
综合HV 和IGD+的统计数据分析结果.WFG1 的设计是带有偏见和混合结构的PF,R2-RVEA 的总体性能良好,要明显优于对比算法.WFG2 是一种带有断开的PF,R2-RVEA 在这个测试问题上表现了不错的性能,在5 目标数和10 目标上要明显优于对比算法.WFG3 是一种比较难处理的问题,具有退化的PF 且决策变量不可以分离,在这个问题上,R2-RVEA 的HV 值要优于所有的对比算法,但是在15 目标上所有对比算法的HV 值都是0,因此在这一目标上无法进行性能对比.
WFG4-9 都被设计为凸面的PF,但在决策空间上具有不同的难度.从表4 和表5 中可以看出,R2-RVEA 在WFG4 测试问题获得了最优的性能.在WFG5 问题上,R2-RVEA 获得了较好的性能,相较于其他对比算法性能稳定.对于WFG6 测试问题,所有对比算法性能相似,R2-RVEA 的性能略优于其他算法.在WFG7 上,R2-RVEA 仅在15 目标上获得了最好的性能,而TS-R2EA 总体性能要明显 优 于R2-RVEA.并 且R2-RVEA 在WFG8 测 试问题上的性能和NSGA-III、RVEA 和TS-R2EA 相似,但明显优于其他对比算法.在WFG9 测试问题上,除了RVEA 和TS-R2EA,R2-RVEA 在所有目标上要明显优于其他对比算法.综合统计结果可以看出,R2-RVEA 在WFG 测试集上总体性能优越.
3.4 算法性能分析
从上面两个测试集得出的实验结果可以看出,提出的R2-RVEA 在DTLZ 测试集中展现了比较不错的性能,在WFG 测试集上性能非常优异.表6 总结了所有算法在64 个测试实例中的实验对比,可以看出本文所提出的算法性能优越.
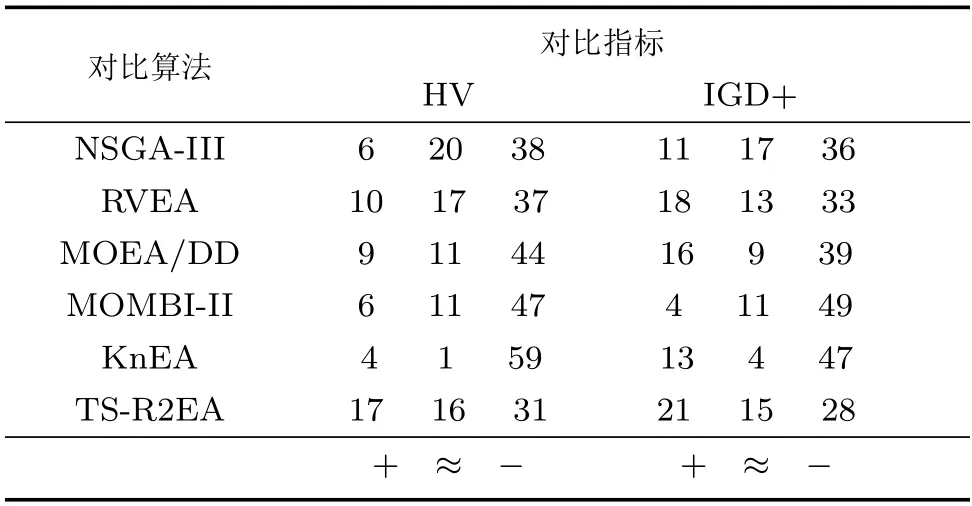
表6 R2-RVEA 与其他算法的测试对比Table 6 Comparison between R2-RVEA and other algorithms
当然,提出的算法仍然存在不足之处,经过实验分析可知算法在指导进化种群的时候,存在收敛到局部PF 而无法有效管理多样性的情况,使得算法性能急剧下降.
算法前期仅考虑收敛性,仅当整个种群收敛到PF 以后才管理多样性,可能导致整个种群都收敛到局部的PF 上,后面再采用种群分解和R2 排序也无法有效管理多样性.在多次实验过程中发现R2-RVEA 会出现稳定和不稳定这两种情况,具体可见图6 中R2-RVEA 在3 维DTLZ7 上的实验,对于GD 指标,GD 值越小说明收敛性越好,两种情况GD 指标进化轨迹基本相同,这说明两种情况的收敛性基本相同;对于DM 指标,DM 值越大说明多样性越好,可以看出R2-RVEA 在不稳定情况时DM随着进化过程数值骤减,最终DM 明显小于稳定情况的DM 值,说明了多样性要明显比稳定情况时候的差.通过图5 可以直观地看到R2-RVEA 在不稳定情况时种群收敛到局部PF,这时候DM 值骤减到比较小的水平,也是导致多样性较低的主要原因.

图5 R2-RVEA 在3 维DTLZ7 上获得的不同结果Fig.5 Different results obtained by R2-RVEA on 3-objective DTLZ7
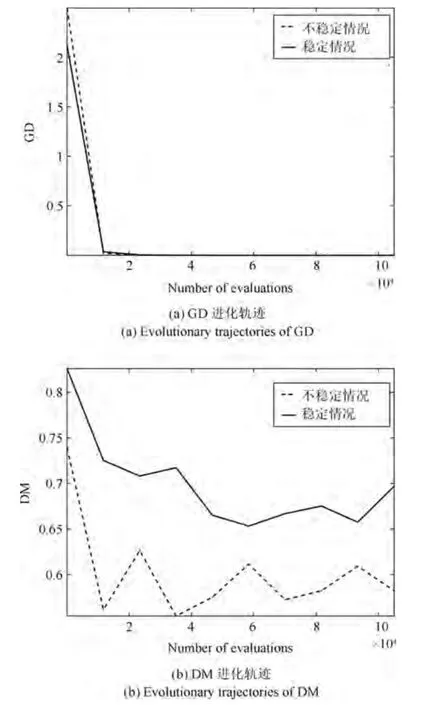
图6 R2-RVEA 在3 维DTLZ7 上GD 和DM 指标的进化轨迹Fig.6 Evolutionary trajectories of GD and DM for R2-RVEA on 3-objective DTLZ7
4 结束语
本文提出了一个基于R2 指标和参考向量的高维多目标进化算法.这个算法致力于处理具有不同PF 形状的MOPs 以及MaOPs.在算法中,为了让种群可以快速地收敛到PF 上,采用了Pareto 支配选取当前种群非支配解的方式来指导整个种群优化.而当整个种群都收敛到PF 上以后,采用种群分解和R2 排序进一步管理种群的收敛性和多样性.
实验结果表明了提出的R2-RVEA 在处理具有不同PF 形状的MOPs 以及MaOPs 时,能够很好地平衡收敛性和多样性.当然,算法的初期阶段仅采用Pareto 支配选取最优解的方式有可能导致种群收敛到局部PF 的情况发生,这使得种群分解和R2 排序已经无法有效地管理种群的多样性.因此,在保证种群稳定地收敛到PF 上,如何更好地管理种群的多样性仍然是未来工作的一个方向.
