一类非线性分数阶微分方程的幂级数求解

金艳玲

(山西工程科技职业大学 基础课教学部，山西 晋中 030619)

分数阶微分方程应用广泛，尤其在物理、化学、生物学等方面作用突出.因此，探讨微分方程的求解方法非常重要，而事实上，绝大部分分数阶微分方程的精确解都无法获得，所以将问题转化为寻求方程的数值解.一直以来，就有很多学者在分数阶微分方程的数值解方面都做了大量的研究.文献[1]中，采用了基本的分数差分法、Adomain分解法和变分迭代法对一类常系数线性分数阶微分方程的数值解进行了讨论，并用数值算例给出各种方法计算效果的对比结论.而文献[2]则利用样条插值法讨论了非线性微分方程的数值解.文献[3]使用分数样条法求解了分数阶微分方程组的数值解.文献[4-8]作者利用了小波分析方法，将分数阶微分方程求解得以有效解决.

Taylor展式是处理很多复杂函数的有效工具，其优势在于能将任意可导函数转化为幂级数形式，进而实现数值计算，而恰好幂函数的分数阶微积分是简单的，所以本文探讨在一般的分数阶微分方程中，将方程的分数阶微分项利用幂级数展开，得到近似值，进而求出方程的近似解.

1 基础知识

1.1 定义

分数阶微积分在发展历史有很多定义形式.最早出现的是 Riemann-Liouville分数阶积分算子

J0f(x)=f(x)

进而给出微分定义：

但随着研究的深入， Riemann-Liouville分数阶微分的弊端不断显现出来，随后由Caputo给出了函数f(x)的分数阶导数的新定义：

本文中，我们所讨论的微分方程为Caputo意义下的分数阶导数.

1.2 方程

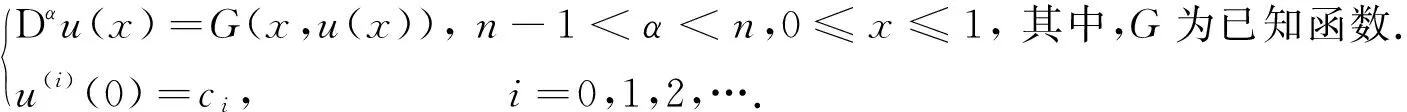
针对该类型方程，本文将分数阶项利用Taylor展式展开，进而获得u(x)的数值解.

2 算法讨论

2.1 定理

设函数u(x)为任意阶可导，则其分数阶导数有如下的近似结果

证明 由Taloy展式可知，对任意x∈(0,1)，有

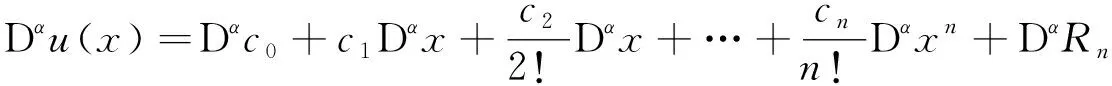
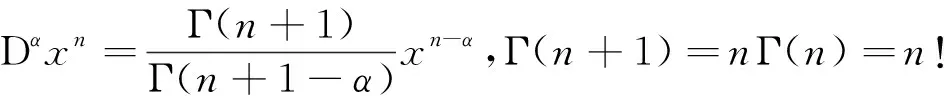
所以，很容易获得定理结论.

2.2 误差

3 数值算例

u(x)=2x+1.

首先，我们将等号左边的u(x)利用幂级数展开，运算得到

获得u(x)的数值解，与真值得对比如表1.

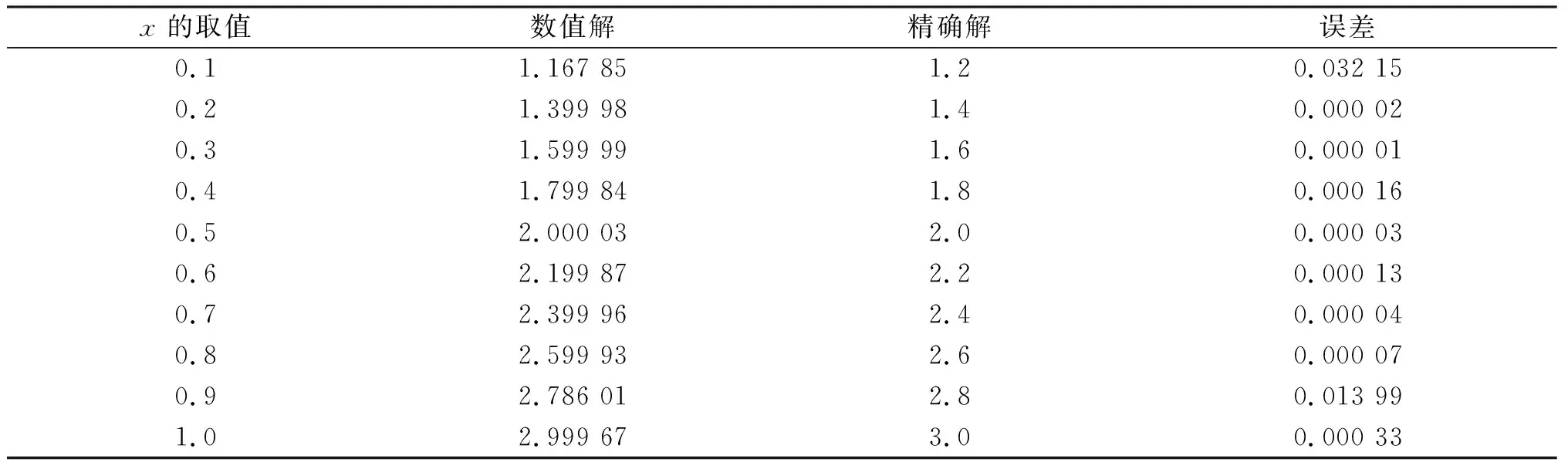
表1 算例1数值解与精确解对比

进而利用Matlab软件编程，得到数值解与真值的图形见图1.

由此可见，所讨论方程的数值解与真值之间误差较小.

算例2 为了验证该方法的广泛使用性，以下我们考虑方程

经过讨论可知，该方程的精确解为u(x)=2x3-x.

利用上述方法，编程得到真值与数值解之间的对比图象如图2.

图1 算例1真值与数值解对比图2 算例2真值与数值解对比

通过以上两个具体的例子可以看到，这种利用幂级数的近似求解方法对求解非线性分数阶方程的数值解行之有效.