基于电压波动特征聚类的配电网拓扑识别方法
2022-01-07文玉兴余永胜
海 迪,崔 娇,文玉兴,余永胜,刘 苏,黄 纯
(1.云南电网有限责任公司昆明供电局,中国 昆明 650011;2.湖南大学电气与信息工程学院,中国 长沙 410082)
准确的配电网拓扑结构是配电网运行、管理及故障抢修等的基础[1]。低压台区用户繁多,接线复杂,拓扑数据目前大多由人工录入计算机系统,准确率较低,且缺乏有效的校核手段[2]。随着社会经济的发展,居民用电负荷快速增长,低压台区电力设施迁建、扩容等变动日益频繁,计算机系统中用户-配电变压器的从属关系(以下简称户变关系)和用户的相别关系难以人工及时更新,亟需有效的配电网拓扑自动识别和校验方法[3-5]。
目前配电台区拓扑自动识别方法可以归纳为2类:1)利用拓扑识别仪的方法;2)利用智能终端采集的电气量数据的方法。前者基于拓扑识别仪发出的载波信号进行拓扑关系校验,需要增加设备投资,难以大规模推广应用[6,7]。后者利用配电网已有的智能终端采集的电气量,通过智能算法进行拓扑识别,不需要增添额外设备,是目前学术研究和工程采用的主流方法。
文献[8,9]基于量测的电压数据,采用智能算法校验拓扑关系,但算法相对繁琐。文献[10-12]基于电压数据的相关性分析,根据同一台区内电气距离较近,用户电压序列相似性较大的原理,对用户所属台区进行校验;但是当不同台区内用户电压接近时,该方法可能会存在误判。文献[13-15]基于AMI的量测信息进行户变识别,相较于只是电压信息分析更全面。文献[16]基于离散Fréchet距离和剪辑近邻法降低拓扑搜索复杂度,可操作性高,但是需要对数据进行训练,所需数据量大。文献[17]基于多元线性回归对电气量数据建立回归关系,从而找到正确的拓扑关系,简单易行。文献[18]基于BIRCH聚类方法对单相用户的相别关系进行聚类,聚类结果准确,但是聚类方法相对复杂。文献[19,20]基于同相用户功率之和与该相首端功率基本平衡的假设,通过优化各相用户的组合达到功率最佳平衡,从而进行用户相别辨识,但存在小功率用户时辨识准确性不高。
本文提出一种基于电压波动特征聚类的配电网拓扑识别方法。首先,分析了配电台区的电压波动特性,定义了能反映电压波动全局和局部特性的特征参数集,给出了其计算方法;然后,提取邻近台变电压及其用户电压的多维波动特征参数,并采用t-分布随机邻近嵌入(t-distributed stochastic neighbor embedding,t-SNE)算法对高维电压波动特征数据降维;最后,基于降维后的电压波动特征,采用改进K-means算法对台变和用户聚类,实现配电网户变关系和用户相别的辨识。相比于传统直接采用电压数据进行聚类的拓扑识别方法,本文所提方法的拓扑识别准确率更高,解决了不同台区电压接近时拓扑不能正确识别的问题。
1 电压波动特征参数
1.1 配电网拓扑识别原理
在配电网中,台区配电变压器(以下简称台变)智能终端和用户智能电表能按照预先设定的时间间隔(一般为15 min)记录台变低压侧三相电压和单相用户电压的有效值,并通过通信网络将电压信息传送到数据中心。本文利用智能终端采集的台变电压和用户电压数据进行拓扑关系识别。
受负荷及其它多因素的影响,台变电压和用户电压随时间发生波动。电气距离比较近的节点电压波动曲线相似性比较高,而电气距离比较远的节点电压波动曲线相似性较低。因此,同一台区内用户的电压曲线波动相似性较高,同一台区同一相上的用户的电压曲线波动相似性更高,而不同台区的用户电压曲线波动相似性较低。本文依据这一原理对用户所属台变和相位进行识别。
1.2 电压波动特征参数及计算方法
目前,传统方法通过比较各电压曲线的波形相似性来进行拓扑识别,采用欧式距离、DTW距离等来衡量曲线间的相似度。该类方法本质上是比较电压曲线(序列)的全局特征,而忽略了波形趋势变化、波形局部起伏变化等细节信息。对波形局部特征的分析不足,在不同台区电压值接近时,不同台区电压曲线间的区分度不高,导致识别结果很容易出现错误。本文定义能反映电压曲线全局变化特性和局部变化特性的多特征参数,通过电压曲线的局部变化特征增大不同台区用户的区分度,从而提高不同台区电压值接近时的配电网拓扑识别正确率。
对于电压曲线序列X={x1,x2,…,xm},提出如下电压波动的特征参数,全面、精细刻画电压波动的全局特性和局部特性:
(1)电压标准差Std,反映电压序列X的离散程度:
(1)
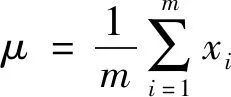
(2)电压曲线峭度Kurtosis,即电压序列X的4阶标准矩,反映电压数据的分布特性:
(2)
(3)电压曲线偏度Skewness,即电压序列X的3阶标准矩,反映电压数据分布偏斜方向及程度:
(3)
(4)电压曲线斜率Slope,反映电压序列X在每一采样时刻i的电压波动趋势:
(4)
(5)波谷位置相同数NSTP(Number of Same Trough Position),波谷位置表示电压波形的极小值点,一方面反映电压波形即将升高的位置;另一方面反映电压局部最小值。两个电压波形的波谷位置相同的点的数目,可精细反映两电压曲线波动起伏的局部相似性。如果两个电压序列相近,那么这两个电压序列与所有样本电压序列的波谷位置相等数组成的序列也具有强的相似性。
(6)波峰位置相同数NSPP(Number of Same Peak Position),在采集时间内波峰位置表示电压波形的极大值点,一方面反映电压波形即将下降的位置;另一方面反映局部最大值。通过统计两个电压波形的波峰位置相等数,可得到两电压曲线波动起伏的局部特征。
设参与拓扑识别的n个电压序列为Y1,Y2,…,Yi,…,Yn;其中,电压序列Yi={yi1,yi2,…,yim},m为序列Yi的长度(即分析时间内电压采样点数)。
对于电压序列Yi,由其标准差、峭度、偏度、斜率、波谷位置相同数和波峰位置相同数等电压波动特征组成的组合参数Ci为
Ci=[Stdi,Kurtosisi,Skewnessi,Slopei,NSTPi,NSPPi],
(5)
式中:参数Stdi,Kurtosisi,Skewnessi和Slopei均可根据电压序列Yi自身求出,见式(1)~(4)。
电压序列Yi的特征参数NSTPi和NSPPi为长度为n的序列,需要与所有参与拓扑识别的n个电压序列(包括台变三相电压和用户电压)比较获得:
NSTPi=[countT(Yi,Y1),countT(Yi,Y2),…,countT(Yi,Yj),…,countT(Yi,Yn)],
(6)
NSPPi=[countP(Yi,Y1),countP(Yi,Y2),…,countP(Yi,Yj),…,countP(Yi,Yn)],
(7)
式中:countT′(Yi,Yj)、countP(Yi,Yj)分别表示电压序列Yi与Yj的波峰、波谷位置相同点的数目。
对每一个参与拓扑识别的电压序列进行上述处理,得到它们的特征组合参数;然后,由各电压序列的特征组合参数构成所有电压序列的波动特征矩阵D=[C1;C2;C3;…;Ci;…;Cn]。该矩阵维数为s×n,其中s=2n+(m-2)+3=2n+m+1,其中n为电压序列个数,m为每个电压序列的长度(即电压采样点数)。
不同的电压曲线波动特征参数的幅值具有很大的差异,为了避免将不同幅值的参数进行比较,需对数据进行归一化,将有量纲的值转换成无量纲的值。对波动特征矩阵D中的特征参数按列进行最值归一化,其归一化表达式为[21]
(8)
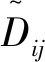
2 配电网拓扑关系识别
2.1 t-SNE特征降维
对于每一个电压序列,其特征参数维数大,直接利用特征参数进行拓扑识别计算复杂,且可视性不好。针对这一问题,本文引入t-SNE算法[18]对电压特征参数进行降维。
作为一种非线性的降维方法,t-SNE算法只需给出高维数据和目标维数即能得到降维后的低维数据,非常适用于高维数据降维到2维或者3维,便于进行可视化。
t-SNE算法使用概率分布函数将参与拓扑识别的电压序列的波动特征参数间的欧式距离转化成概率相似度,从而使用概率分布矩阵描述台区电压的分布特性;然后,使用高斯分布函数对低维电压波动特征进行转换。最后,根据高维概率分布矩阵间的KL散度评估分布一致性,即低维电压波动特征集是否在分布上与原始高维电压波动特征集保持一致;若达到了一致性,则不改变电压序列波动特征相似性的基础上,对电压波动特征完成了降维。
对于电压序列Yi,本文采用t-SNE算法将其s=2n+m+1维的波动特征组合参数Ci降维为2维的特征参数Ei=[Pi,Qi],然后基于特征参数Pi和Qi进行拓扑识别。
2.2 基于K-means聚类算法的拓扑识别
本文利用K-means聚类算法[22]进行拓扑识别。K-means算法是一种无监督的迭代求解的聚类分析算法,一般采用欧氏距离来度量样本间的相似度,其实现步骤是:将样本预分为K组,随机选取K个样本作为初始的聚类,然后计算每个样本与各聚类中心之间的距离,把每个样本分配给距离它最近的聚类中心。聚类中心及分配给它们的样本就代表一个聚类。每分配一个样本,聚类中心会根据聚类中现有的样本重新计算,此过程不断重复直到满足终止条件:没有(或最小数目)样本被重新分配给不同的聚类,没有(或最小数目)聚类中心再发生变化,或误差平方和局部最小。
K-means算法易于实现,且效率高,在许多工程领域聚类效果好,得到广泛应用;但其也存在一些缺点,例如:聚类个数不易获取,聚类结果依赖初始聚类中心的选择,若选取不当易导致算法陷入局部最优而使得聚类不合理。
本文结合配电网拓扑识别问题的具体情况,对K-means算法进行如下改进:1)选取聚类个数K为台区个数的3倍;2)初始3个聚类中心不是随机选取,而是设置为各台变的三相电压序列的2维特征参数。
2.3 拓扑识别的实现步骤
对待校验用户拓扑关系的识别步骤如下:
(1)从配变终端获得台变低压侧电压时间序列数据,从用户智能电表获得相同时间段内台区各用户的电压时间序列;
(2)对采集的一定时间内的用户和台变的电压序列进行处理,提取电压波动特征参数;
(3)采用t-SNE方法对步骤(2)中获得的电压波动特征进行降维,得到2维的电压波动特征;
(4)利用K-means聚类算法,基于2维电压波动特征,对台变电压和用户电压变进行聚类;
(5)根据聚类结果,确定用户与台区的从属关系以及用户的相别。
3 仿真分析及方法验证
3.1 低压配电台区拓扑结构
某配电网拓扑结构如图1所示。采用Matlab/Simulink建立两个低压配电台区的仿真模型,两个台区中台变变比均为10 kV/0.4 kV,台变T1低压侧三相电压分别用U1A,U1B和U1C表示,台变T2低压侧三相电压分别用U2A,U2B和U2C表示。节点1~25表示25个用户。其中用户1~4、用户5~8和用户9~13分别接在台变1的A相、B相和C相,用户14~16、用户17~20和用户21~25分别接在台变2的A相、B相和C相。
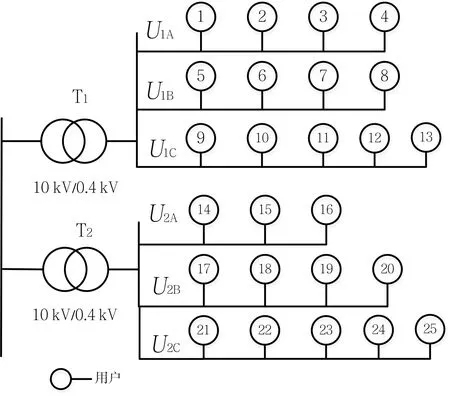
图1 低压配电网拓扑结构图Fig. 1 Low-voltage distribution network topology diagram
按15 min 1次的间隔在2~5 kW间随机给出该台区各用户的有功功率值,并假定用户的功率因数为0.9~0.95。通过仿真,获得台变低压侧三相电压及2个台区用户电压的有效值,如图2所示。
图2为一天内2个台变的低压侧三相电压曲线及25个用户的电压曲线,其数值接近,波形相似,采用常规方法利用电压曲线的整体特征难以有效识别出台变与用户的拓扑关系。
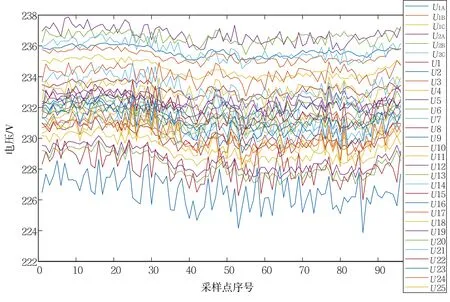
图2 台变和用户电压曲线Fig. 2 The voltage curve of transformers and users
3.2 对电压波动特征进行降维
根据2个台变三相电压序列和25个用户电压序列(共31个电压序列)计算电压波动特征矩阵,再采用t-SNE算法将得到的高维电压波动特征矩阵转化为2维电压波动特征P和Q。各电压序列的P和Q值如表1所示。
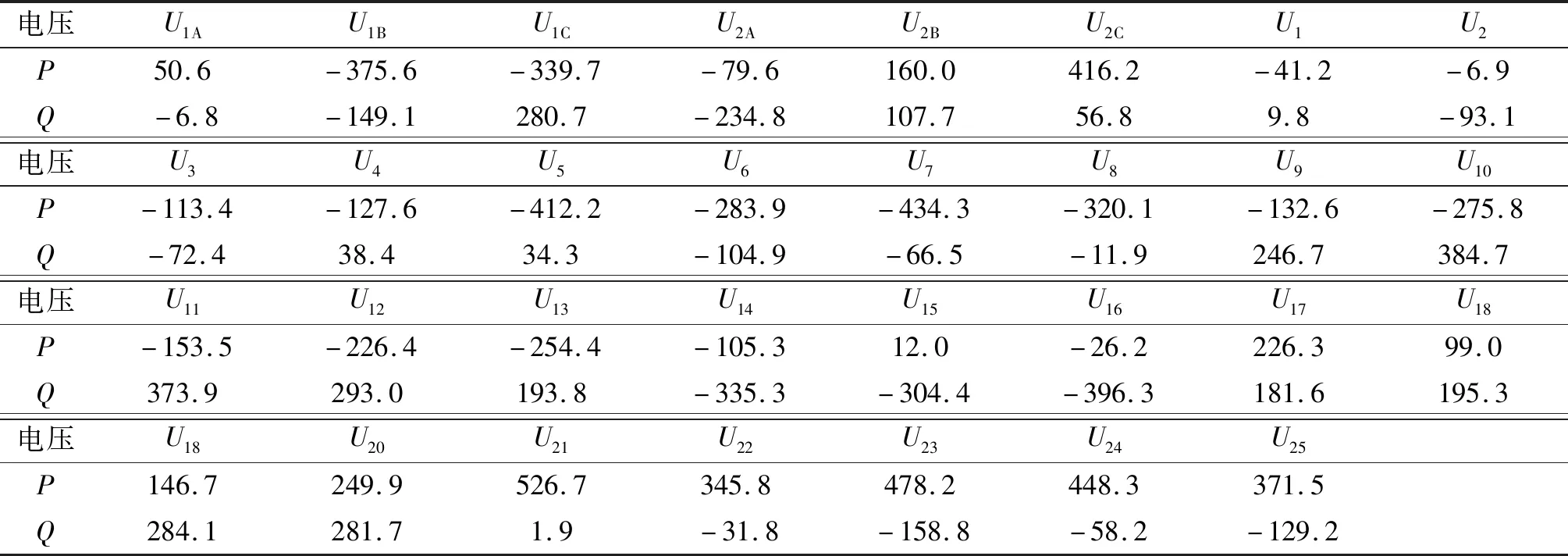
表1 各电压序列的低维波动特征P和QTab. 1 Low-dimensional fluctuation characteristics P and Q of each voltage series
3.3 电压序列的聚类结果
采用K-means算法,直接对2个台变的三相电压序列及25个用户的电压序列(共31个电压序列)进行聚类,聚类结果见表2。表2显示,用户所属台变及相别与图1中设置不一致,说明仅利用电压序列的整体特征进行聚类,无法正确区分出如图1中电压数据总体较为相近的电压序列。

表2 电压序列的直接聚类结果Tab. 2 The results of direct clustering for voltage series
对所有31个电压序列的电压波动特征参数(表1中P和Q)降维后采用K-means算法进行聚类,聚类结果如表3所示。图3为31个电压序列在P和Q坐标系中的分布情况。
表3和图3均显示:用户1~4的电压序列与台区1的A相电压序列聚类为同一簇,即用户1~4属于台区1的A相;同理,用户5~8属于台区1的B相,用户9~13属于台区1的C相,用户14~16属于台区2的A相,用户17~20属于台区2的B相,用户21~25属于台区2的C相,这与图1设置情况一致。至此,利用电压多维波动特征聚类不仅准确地识别出了用户所属台变,而且准确地识别了用户的相别。

表3 电压序列的波动特征降维后的聚类结果Tab. 3 The clustering result after dimensionality reduction of fluctuation characteristics for voltage series
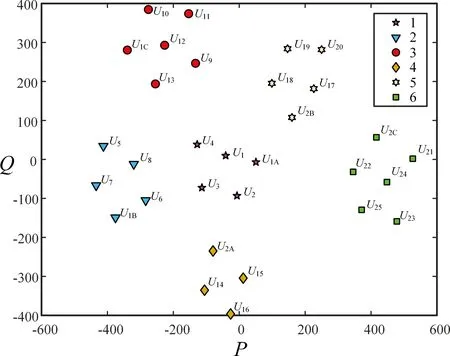
图3 电压波动特征聚类结果Fig. 3 The clustering results of voltage fluctuation feature
4 结论
本文提出了一种基于电压波动特征聚类的配电网拓扑识别方法。该方法具有以下特点:
1)定义电压波动特征参数集,精细刻画了配电网电压波动的全局特征和局部特征;利用新的波动特征参数进行拓扑识别,解决了不同台区电压接近时拓扑识别困难的问题,显著提高了拓扑识别的正确率;
2)采用t-SNE算法对台变和用户电压的多维波动特征进行降维,在保留用户与台变电压波动基本特性的基础上,解决了电压数据维数过高,聚类计算时间长的问题;
3)采用K-means算法利用降维后的电压波动特征进行聚类,不需要人为设定阈值,可准确识别户变关系和相别关系;
4)本文方法利用配电网已有智能终端的历史电压数据对拓扑结构进行识别,不需要新增设备,减少了投资,同时降低了运行人员的劳动强度。
