基于改进狼群算法的光纤测试中光谱重叠优化研究
2022-01-07曲鸿春贺开放王亚坤赵子玮
刘 邦,曲鸿春,贺开放,王亚坤,冯 豆,李 强,赵子玮
(1.国网安徽省电力有限公司亳州供电公司,安徽 亳州 236800;2.三峡大学,湖北 宜昌 443002)
0 引言
与传统变电站相比,智能变电站采用以光纤作为传输介质的通信技术,具有更好的兼容性和可靠性。智能变电站建立网络化的通信系统,将传统的电子信息转换为数字信息,提高了电力网络的智能化程度和运维可靠性。智能变电站复杂的通信系统对运维人员提出了新要求:光纤通信故障时需迅速准确定位故障地点,以便快速修复。布拉格光纤光栅(Fiber Bragg Grating,简称FBG)技术具有抗电磁干扰、高性价比、高灵敏度等优点,可用于检测温度、位移、振动等物理量,包括时分复用、波分复用、空分复用、谱形复用等类型,能够满足电力生产、土木工程、航空航天等领域的不同需求。
FBG谱形复用是基于识别光谱形状信息对光谱进行解调,允许光谱重叠,可以在有限的光源带宽内提高FBG传感器的复用数量。解调算法是实现FBG谱形复用的关键,目前较多学者采用不同的优化算法来提高解调的准确性。文献[1]通过改进模拟退火算法中的退火因子及回温操作,并与粒子群算法相结合对光谱重叠中的各个光栅进行识别。文献[2]采用粒子群算法探究关键参数对解调效果的影响。文献[3]采用大数据分析技术对光谱信息进行预处理,并用粒子群算法在2个FBG传感网络内进行优化复用并解调。文献[4]对光纤滤波器模型与控制电压之间非线性和回滞特性进行了研究,对多个FBG复用系统重叠光谱进行识别。上述研究成果,虽然使用智能算法完成了FBG谱形复用,但是存在识别精度较低及FBG复用传感网络数量不多的局限性。为此,本文提出基于狼群算法解调中心波长,并引入学习因子和变异系数,跳出局部极值以增强全局搜索能力,对多个FBG复用系统进行解调,提高了解调精度。
1 FBG谱形复用解调原理
通过FBG谱形复用采集光谱形状信息,当FBG感应到外部条件发生变化时,光谱形状不变,波长产生一定漂移[5]。在并联光谱复用系统中,光源发射的光通过耦合器进入n个支路中,再由FBG反射回来,经衰减器调节反射峰值,最终在光谱仪中形成反射光谱,通过反射光谱的识别获取外界条件的变化量[6-7]。并联光谱复用系统结构示意图[8]如图1所示。

图1 并联光谱复用系统结构图
假设第i个FBG反射光谱谱形为gi(λ-λBi),表达式为:

式中:λBi为第i个FBG中心波长;ri为第i个FBG反射率,0≤ri≤ 1;BG为3 dB带宽,一般取0.2 nm。
则光谱仪中叠加光谱表示为:

式中:R为叠加光谱的函数,即采样光谱;g为超高斯函数;N(λ)为系统中的随机噪声。
由于式(2)中的谱形可能会发生完全重叠、部分重叠和不重叠的情况[9-10]。为了方便解调中心波长,对原始反射光谱进行重构,构成的新光谱表示为:
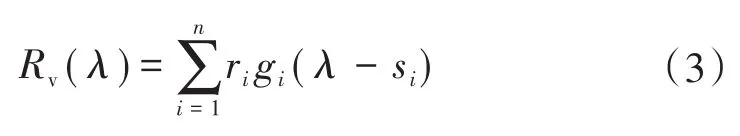
式中:si为第i个FBG的重构光谱的中心波长。
将Rv(λ)和R(λ)进行比较,得到光谱重叠程度的函数:

当si=λBi时,目标函数f()s取最小值。将求解中心波长的过程转化成求解最优值,原始光谱和重构光谱达到最优匹配时,即求出中心波长值。
2 改进狼群算法在光纤测试中的应用
2.1 狼群算法
为使原始光谱和重构光谱达到最优匹配,将向量si=(s1,s2,s3...,sn)作为优化参数,f(s)作为优化目标函数。
狼群处在N×D的空间内,N为狼群数量的总数,D为空间维数,则任一狼的位置为:

式中:r为[0,1]区间内均匀分布的随机数,xmax和xmin分别表示搜索空间的上限和下限。
通过游走行为来更新探狼的信息,探狼i向第p(p=1,2,⋅⋅⋅,h)个方向前进一步记录当前猎物浓度。探狼i在d维空间中的位置更新:

探狼搜索的猎物气味浓度Yi大于头狼搜索的猎物气味浓度Ylead时,取代成为新的头狼。头狼发现猎物后会召唤猛狼。猛狼在途中搜索的猎物气味浓度Yi大于头狼搜索的猎物气味浓度Ylead时,也会取代成为新的头狼,执行新的召唤行为。猛狼在d维空间中的位置更新为:

若待寻优变量的第d(d∈[1,2,3 ⋅⋅⋅D])维的取值范围为[dmax,dmin],则距离公式为:
式中:w为距离判定因子。
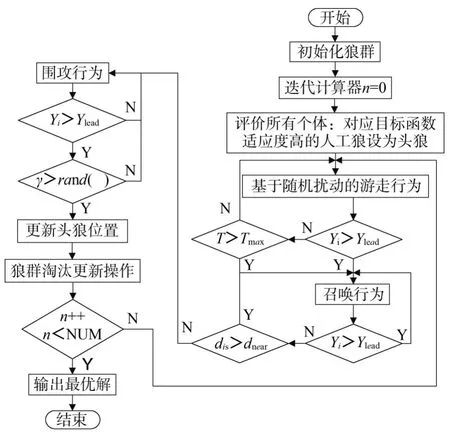
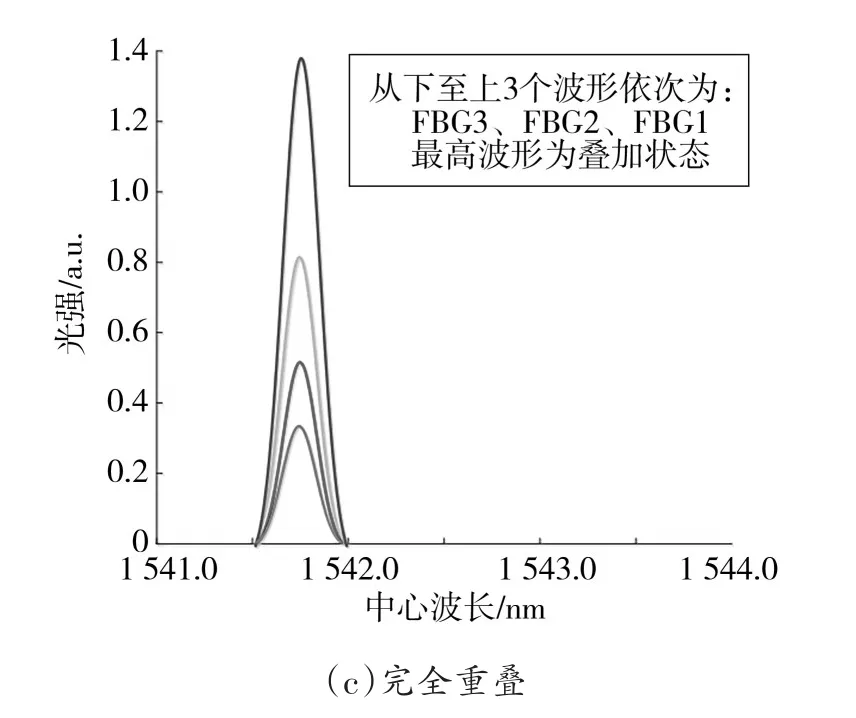
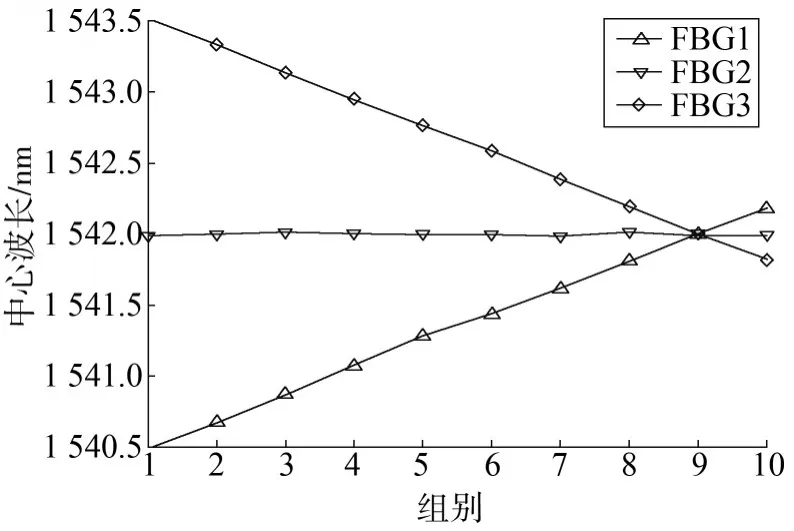
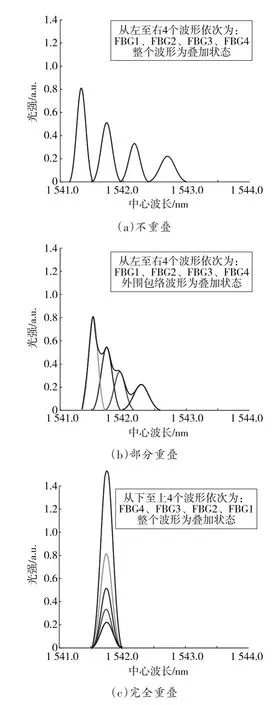
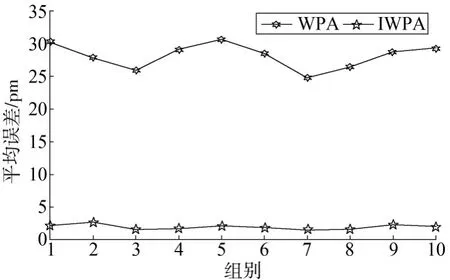
当dis 游走行为、召唤行为、围攻行为的步长公式为: 式中:S为步长因子。 在整个狼群进化的过程中,淘汰目标函数值最差的R匹狼,同时随机生成R匹狼进行补充。其中R∈[n/(2 ×β),n/β],β为狼群更新时的比例因子。 2.2.1 基于随机扰动算子的游走行为 在游走行为中,当h不断增大时,寻优的范围也逐渐扩大,收敛速度会受到影响。本文引用一个随机扰动算子来提升探狼的全局搜索能力。改进后探狼的位置更新为: 其中,β取整数,作为一个随机的扰动,取0、1或-1对探狼的游走行为进行随机扰动,提升寻优范围和速度。 2.2.2 基于模拟退火的围攻行为 在狼群的围攻结束后计算狼群的适应度来替代头狼,这种做法容易使算法陷入局部极值。本文采用模拟退火的方法,对是否产生新头狼进行选择,避免算法陷入局部最优。 围攻行为结束后,若Yi>Ylead,则执行模拟退火过程。通过Metropolis准则选择是否替代头狼。概率判断标准γ(γ≤1)为: 若rand()<γ,则猛狼i替代头狼,反之不执行替代操作。通过模拟退火算法判断过程,将适应度大于头狼的猛狼进行模拟退火考察,避免算法整体陷入局部最优。 算法控制流程如图2所示。 图2 改进狼群算法控制流程图 根据图1所示搭建实验平台,第一组实验采用FBG1、FBG2、FBG3传感器,其中心波长分别为1 541.398 nm、1 541.743 nm和1 542.223 nm。调节FBG1温度在25~70℃变化,将FBG2置于25℃恒温环境下,调节FBG3温度在20~25℃变化。调节衰减反射率r1、r2和r3分别为1.00、0.82和0.63。3个FBG光谱重叠图如图3所示。 图3 3个FBG光谱重叠图 采用WPA(Wolf Pack Algorithm,简称WPA)算法和IWPA(Improved Wolf Pack Algorithm,简称IWPA)算法分别进行10次运算并取平均值,得出各FBG的10组中心波长。中心波长的解调结果如图4和图5所示。 图4 WPA算法解调结果 图5 IWPA算法解调结果 由图4和图5可见,WPA算法解调效果波长误差较大,呈现出较大的非线性;IWPA算法解调效果波长误差浮动较小,具有一定的线性关系。 第二组实验加入FBG4传感器,其中心波长为1 542.751 nm,调节衰减反射率r1、r2、r3和r4分别为1.00、0.82、0.63和0.40。4个FBG光谱重叠图如图6所示。 图6 4个FBG光谱重叠图 采用WPA算法和IWPA算法,在随机的温度变化下分别进行10次运算并取平均值,得出各FBG的10组中心波长。运算后中心波长的解调平均误差和平均耗时情况如图7和图8所示。 图7 WPA和IWPA解调FBG平均误差 图8 WPA和IWPA解调FBG平均耗时 由图7可见,WPA算法解调中心波长的误差在30 pm左右,具有较大的波动性;IWPA算法解调中心波长误差在3 pm上下浮动,相对误差较小且稳定。由图8可见,WPA算法运行平均耗时较长,需要30 s左右;IWPA算法运行速度快,平均耗时均保持在5 s以内。 本文针对智能变电站光纤测试中出现的光谱重叠现象,提出了一种改进的狼群算法,引入扰动因子加强算法的全局搜索能力,并通过模拟退火判断避免了整个算法陷入局部极值的问题。将改进的狼群算法与传统狼群算法相比较,分别对多个FBG进行了光谱重叠的识别,结果表明新算法能够精确识别中心波长,且具备较高的可靠性,保证了智能变电站中光纤通信的稳定。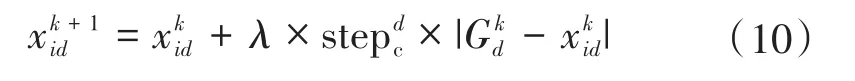
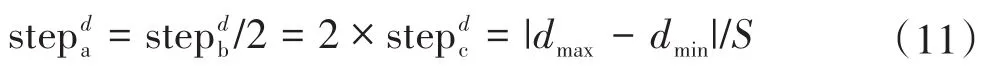
2.2 改进狼群算法在光纤测试中的应用


3 仿真实验与分析
3.1 3个FBG光谱重叠


3.2 4个FBG光谱重叠

4 结语
