一类寄生虫感染的食饵-捕食者模型的数值分析

2022-01-07尤鸿明

泉州师范学院学报 2021年6期

尤鸿明

(1.泉州师范学院数学与计算机科学学院，福建泉州 362000； 2.福建省大数据管理新技术与知识工程重点实验室，福建泉州 362000； 3.智能计算与信息处理福建省高等学校重点实验室，福建泉州 362000)

自20世纪90年代以来，人们对食饵-捕食者模型的动力学性质作了许多研究[1-2].随后，有许多学者也对被寄生虫感染的食饵-捕食者模型作了大量的研究并取得了一些有趣的结果[3-5]. 特别是，Chattopadhyay等在文[3]中提出了种群的持续性和灭绝条件，并确定了周期解的Hopf分支条件.Hethcote等在文[4]中分析了四个被寄生虫感染的捕食者-食饵模型，进一步证明了模型全局稳定性结果.通过修改一个标准的易感染模型，Spencer等[5]分析了生产力如何在一个稳定的寄主-寄生虫模型中调节捕食者饱和和选择性觅食行为所诱导的复杂行为.然而，大多数关于寄主-寄生虫捕食相互作用的理论研究假设行会内的食饵是寄生物种，而不是具有独立成体阶段的寄生虫.Nakazawa等[6]提出了一个寄主-寄生虫捕食相互作用的模型，其中成虫寄生蜂密度以线性功能反应被明确表示出来，并讨论了正平衡点的存在性和局部稳定性.而在本文考虑寄生蜂密度以一般形式g(y)表达，由于寄生虫以及寄主表达的变化，我们的模型必然比以前的模型更加复杂和普遍.

1 模型引入及分析

考虑以下模型:

(1)

其中：S、I、P和Q分别代表未寄生寄主、寄生寄主、寄生蜂和捕食者的密度，γ和K分别代表S的自然增长率和承载能力.参数a12、a13和a23分别表示寄生效率、对未寄生寄主的捕食效率和对寄生寄主的捕食效率.参数η是从单个宿主中出现的寄生蜂数量，δ是捕食者繁殖的转化率.在这里，我们设置捕食者消费未寄生或寄生的寄主的转换率是相同的.最后，dP和dQ分别是寄生蜂和捕食者的死亡.

(2)

以及对应的特征方程为

P(λ)=λ4+a3λ3+a2λ2+a1λ+a0=0.

其中:a3=dp+γ1z*+g′(y*)+x*,a2=α1α2p*x*+(dp-α2ηx*)+g′(y*)+β1β2x*z*+dpγ1z*+

根据Routh-Hurwitz准则，E*是渐近稳定的当且仅当

(3)

由以上的内容，我们得到下面的定理.

定理 2假设模型(2)的正平衡点E*存在.如果式(3)成立，那么E*是渐近稳定的.

2 数值模拟

取g(y)=hy，对式(2)的正平衡点E*的x*和z*可以由以下线性子系统显式求解：

因此，可以直接计算出正平衡点：

(4)

当前，技能竞赛的重要性尚未得到普遍认可，激励机制的建立和完善显得更为重要。我们采取物质奖励和精神奖励相结合的原则，科学合理地设置奖励标准与办法，具体如下。

首先，将参数设置为α2=4，β1=5,γ1=4,γ2=2,h=1,η=1,dz=3,dp和β2范围分别为[0.1,5.0]和[0.0,5.0].然后,利用Routh-Hurwitz 准则,将各平衡点的存在域以及稳定域进行划分.结果见图1～5.

图1 α1=0.1稳定域划分图图2 α1=0.25稳定域划分图Fig.1 α1=0.1 stable domain division diagram Fig.2 α1=0.25 stable domain division diagram

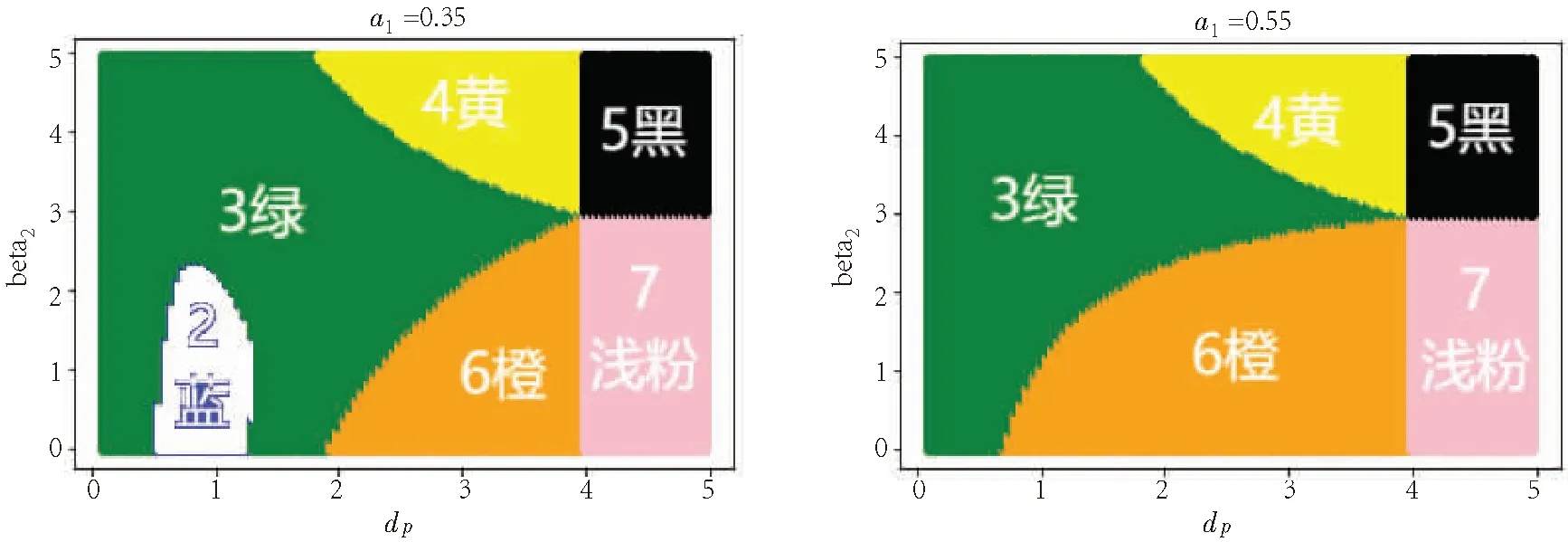
图3 α1=0.35稳定域划分图图4 α1=0.55稳定域划分图Fig.3 α1=0.35 stable domain division diagram Fig.4 α1=0.55 stable domain division diagram

图5 α1=0.75稳定域划分图 Fig.5 α1=0.75 stable domain division diagram

其中，每个平面图的水平轴和垂直轴分别表示dp和β2.图1～5分别取参数α1为0.1,0.25,0.35,0.55,0.75.3绿色区域表示E*稳定；2蓝色区域和1深粉色区域表示E*存在但不稳定，并且E1在2蓝色区域稳定以及E3在1深粉色区域存在但不稳定；E*在4黄色、5黑色、6橙色、7浅粉色和8红色区域均不存在, 但是在8红色区域E2稳定，在6橙色区域E2存在但不稳定，在7浅粉色区域E1稳定，在5黑色区域E3稳定，在4黄色区域E3存在但不稳定.

通过以上的划分，我们发现E*存在于三个区域，分别是1深粉、2蓝色和3绿色区域，并且在图1～2中，这三种区域都比较明显地划分出来.接下来, 我们固定α1=0.25(图2)，dp=1.接着对应三个区域分别取β2=1(2蓝)，β2=3.2(1深粉)，β2=4.9(3绿).因此，我们会得到以下三种情况：