南方CASS软件在土方量计算中的应用

程海港

(华北理工大学，河北 唐山 063210)

引言

土方量计算占据着工程建设中的重要地位，其预算直接影响到工程费用的估算以及方案选优。无论在道路建设工程、水利水电工程还是建筑工程中，都需要预先进行土地整平工作。需要测量人员进行地物特征点数据的提取，将数据输入到CASS中进行展点，运用相关的方法计算某区域内的土方量。合理选择土方量的计算方法使其精确，可以降低纠纷，并提高经济效益。科学选择土方量计算方法可以提高工作效率，对工程项目的推进有促进作用[1]。

20世纪90年代至今，经济发展突飞猛进，基础设施相应的需求量急剧增加，土木工程行业形势大好。土木工程中的“土”字即为土方，因此土方量的计算得到了人们的重视。准确计算土方量是确保项目顺利进行的重要因素，且其预算直接决定工程造价[2]。合理选择土方计算方法使其准确，可以减少纠纷，提高经济效益。

传统的土方计算方法有方格网法、等高线法、断面法、散点法、表格法，计算方式繁琐，计算量大，精度低，并且受地形条件的限制，愈加不能满足人们的要求，为此，相关学者开始对土方量计算方法进行深入研究。随着计算机技术的飞速发展，图像处理技术结合着土方量计算的理论所形成的一种新的研究形式成为了目前主流研究方式[3]。目前，可以通过软件进行的土方量计算方法包括DTM法、方格网法、断面法、区域土方量平衡法。

1 南方CASS中4种计算土方量的方法

1.1 DTM法

DTM法步骤，进行特征点的碎步测量，将所测数据传输到计算机中，用南方CASS展高程点并建立DTM数据模型。DTM法的基本原理是根据实测的特征点的坐标(X,Y,Z)和设计高程来生成三角网，通过计算此三角网中各个三棱锥的填挖土方量，累加得到区域内的总挖填土方量，并在三角网上用复合线勾画出挖填边界。DTM法所建立的模型较为真实，因此精度相对高于其它方法[4]。但是其数据量较大，计算方式较长，存储空间较大。

1.2 方格网法

方格网法的中心思想就是先局部后整体，化整为零再累加。计算小正方形区域内的填挖方量，将其累加得到整体填挖方量，并且用白色线画出挖填边界。展开来说，建立方格网将整个大的测区划分成各个小的正方形区域，分别计算单个正方形区域内的填挖方量。在小正方形区域内，4个顶点的高程相加后除以4，得到平均高程。若顶点的高程没有测得，用内插法计算。将得到的平均高程与设计高程作差可得H，由指定的正方形边长S以及H可得长方体体积V，此体积即为所求的填挖方量。方格网法的设计面可以是平面、斜面、三角网3种情况。方格网法易操作，结果直观，原理简单易懂，因此深受广大测绘工作者喜爱[5]。

1.3 断面法

在工程施工测量过程中，如遇到平场区域为起伏大且狭长的条状地形，选择用断面法，见图1。断面法原理很简单，和方格网法有相似之处，均是由局部到整体，先求一部分，然后累加得到整体的填挖方量。设置一条中轴线LL，然后按相同的距离H设置截面，A1，A2，A3……Ai。计算各个截面的填挖面积，2个相邻的截面之间求出平均填挖面积S，乘以两截面间的距离H即可求得这一区域的挖填方量V，将这些各段区域得到的值进行累加即可得到整体区域的填挖方量。在此，两截面间的距离越近，计算的结果精度越高。如果H趋于0时，这就成了一个二次元微分问题。

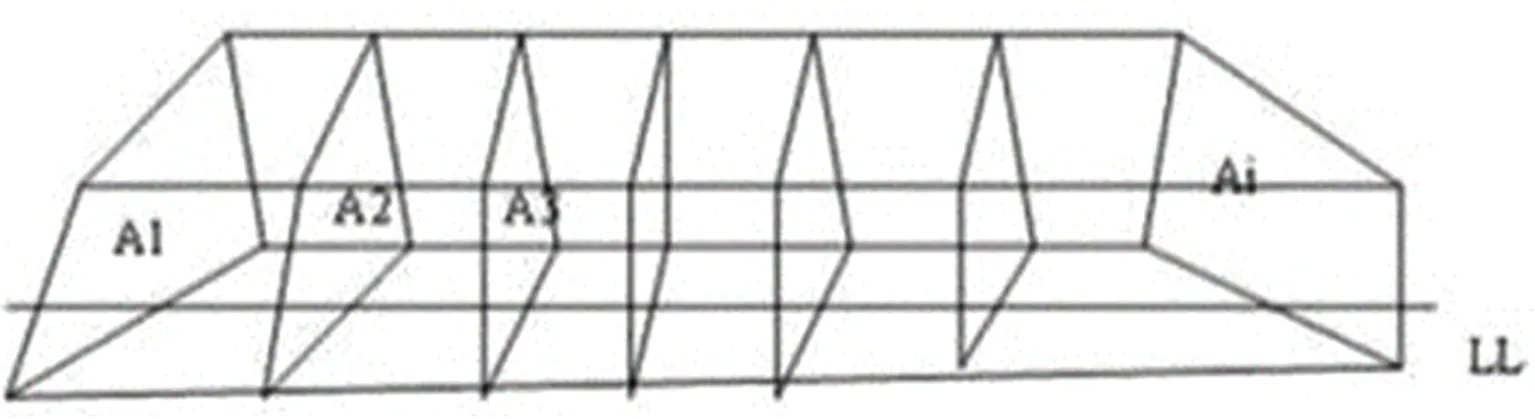
图1 断面法计算土方量

1.4 区域土方量平衡

土方量平衡，即挖方量=填方量，以填挖边界线处为界，将高处挖掉的土方填到低处即可完成场地平整，这样既减少了工作量又降低了运费[7]。

2 案例计算

2.1 测区概况

河南城建学院位于河南省平顶山市新城区，是典型的山地地形，此处选取的测区为河南城建学院一区附近一个三角形区域，测区的数字地形图如图2阴影部分所示。此区域地面起伏较大，在进行高程测量时选取三角高程法。

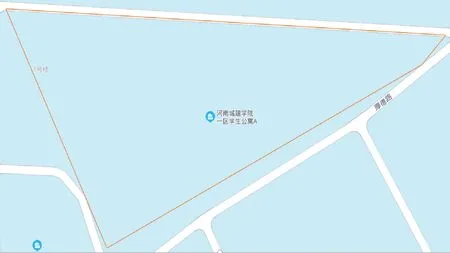
图2 测区数字地形图

2.2 4种方式的土方量计算成果

2.2.1 区域土方量平衡计算

经土石方量计算，得到填方量为692151m3，挖方量为692150m3，见图3a。

2.2.2 DTM法计算土方量

选择DTM法中的“根据图上高程点”计算土方量，得到土方量计算成果如图3b所示。

图3 计算结果

2.2.3 断面法土方量计算

经土石方量计算，得到挖方量为509705.1m3，填方量为521685.9m3，见表1。

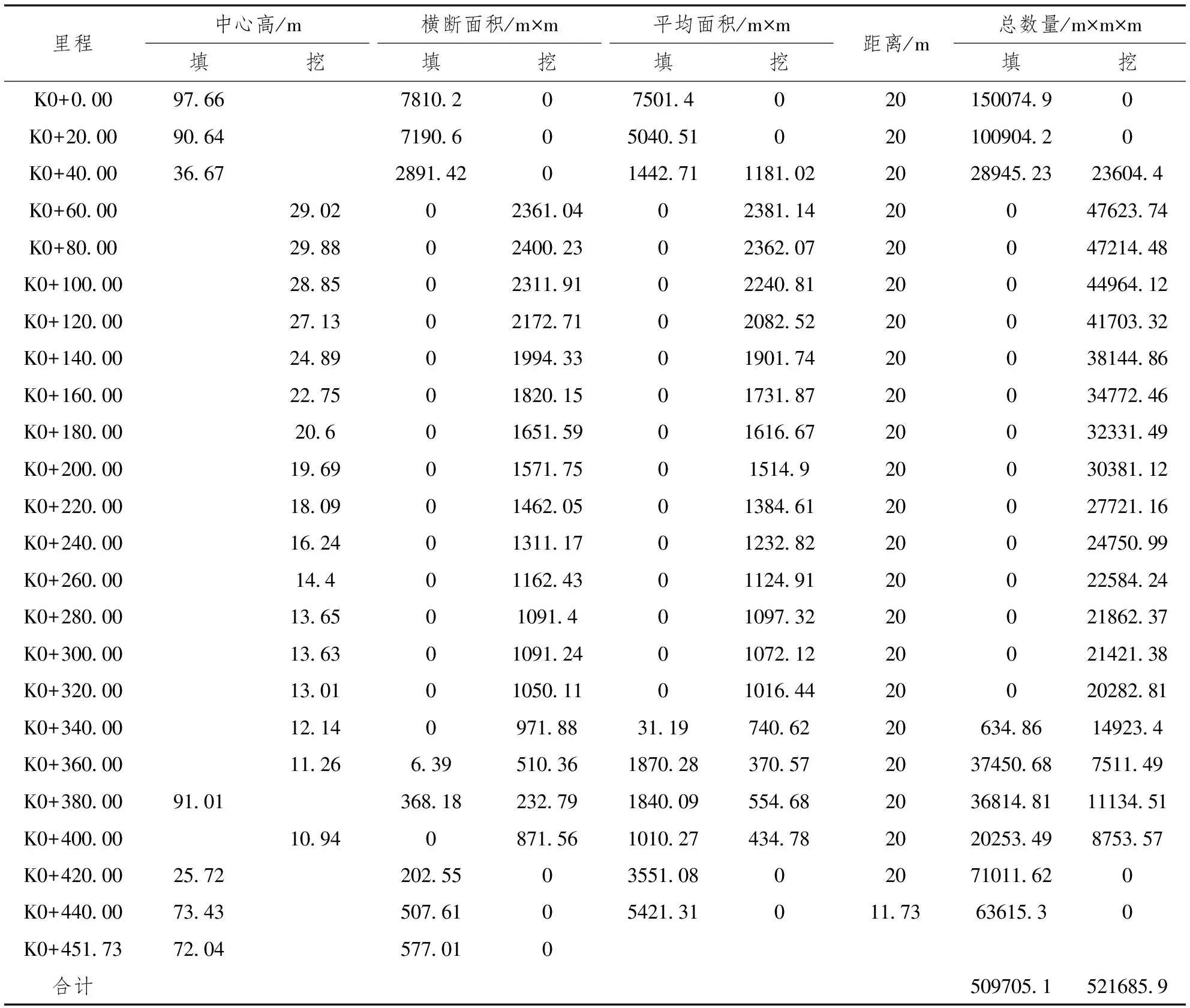
表1 断面法土石方量计算表

2.2.4 方格网法土方量计算

经计算，填方量为650284.7m3，填方量为654027.3m3，见图4。

图4 方格网法计算结果

2.3 精度分析

计算误差，提高计算精度是非常重要的，在实际工作中具有重要意义。如平场区域、采样计算间隔和平场高度的条件相同时，计算相同区域的切割量和填充量，得到平衡线(零线)。并根据区域平衡法的结果，计算了断面法、方格网法和DTM方法的相对精度。相对精度是指断面法、DTM法、方格网法3种方法的挖填方量与区域土方量平衡法的挖方和填方之间进行比较，结果见表2。根据表2计算的相对精度可知，DTM法的精度最高，其成果可用，方格网法次之，断面法最低。

表2 4种土方量计算方法相对精度计算表

3 总结

通过实验得出以下结论。设计高程的选取的问题。想要进行4种方式成果的比较前提是控制变量，即平场面积、计算间隔和平场高程必须相同，最后得到4种方法的计算成果差距不太大时才可进行比较；平场面积以及计算间隔很容易确定，但分别将平场高程设为150.000m和129.164m时，这4种方法的计算结果之间差距太大，显然不能满足精度要求；将区域平衡法计算出的土方平衡高度247.928m设成平场高程时，区域土方量平衡法、DTM法、方格网法3种方法得到的计算结果差距较小，但是断面法得到的填方量依然与之差距很大，可见地形条件限制了断面法的计算精度；以区域土方平衡法为基准计算其它3种方法的相对精度后得出结论，DTM法的精度最高，方格网法次之，断面法最低。区域土方量平衡适用于场地平整；DTM法适用于地形起伏较大的区域以及精度需求高的山地区域，但如果地图本身有大量数据，也要考虑数据存储的问题；断面法适用于复杂地形以及带状区域，如道路、运河，但是其操作较为复杂存在着计算精度与计算速度间的矛盾；方格网法适用于地形平坦的区域，其局限性在于生成的网格会被视为独立的规则表面，因此会与计算站点的实际地形不符，从而造成误差。本文虽然通过多种方法实验得到了各方法的一些适用条件，但仍需更多的工程实例佐证。