基于Stackelberg博弈法的光伏消纳模型设计与仿真计算

刘安诺，井天军，何 欣，王维洲

（1.中国农业大学，北京 100083；2.国网甘肃省电力公司 电力科学研究院，甘肃兰州 730000；3.国网甘肃省电力公司，甘肃兰州 730030）

随着新能源产业的不断发展，光伏发电在电力系统中所占比例不断提高[1]。然而，由于光伏发电存在随机性、波动性等问题，高比例光伏电源的接入，引起了电网的电能质量变差等问题[2]，同时，还导致电网下网的潮流变轻，出现倒送的可能，甚至在严重情况下使部分区域的网供负荷特性发生一定的改变，导致电网供需平衡的难度进一步加大[3]。因此，合理消纳光伏电量成为目前新能源电力发展中亟待解决的问题。文献[4]根据非合作博弈理论，构建了多个微电网调度优化模型，各微网间通过电能交换的方式进行电力转移，在电力不足或富余时可通过从外电网采购或销售电力的方式匹配负荷需求。文献[5]从电力供需侧间互动博弈的角度出发，研究智能用电策略，供电侧可通过调整电价的方式缓解用电高峰时段的供电压力，需求侧可通过对电价的响应，调整自身用电习惯，降低用电成本。文献[6]研究了包含能源运营商、分布式光伏用户、EV 充电代理商等多参与主体的综合能源园区市场交易框架，各方以自身利益最大化为目标进行购售电价的非合作博弈，在平衡各方收益、降低系统用电成本的前提下，达到促进光伏消纳的效果。

光伏消纳模型涉及多方参与，需要建立多目标优化模型，并进行优化计算，现有方法未充分考虑需求响应下的多方博弈均衡状态。该文基于需求响应驱动的弹性矩阵，提出了一种基于Stackelberg 博弈法的光伏消纳模型，建立了多方博弈均衡状态下的优化目标函数，并通过改进粒子群算法进行求解，对模型的有效性进行了验证。

1 光伏消纳模型设计

1.1 电力需求响应弹性矩阵

在实际应用中，需求侧的电力用量具有随电价变化的属性。因此，在基于博弈法的光伏消纳分析中，首先需要建立基于价格驱动的用电负荷转移模型，对这一变化进行定量分析。在该模型中，实际的用电负荷受电价波动的影响。为计算其影响程度，引入了需求响应价格驱动模型。在该模型中，构建了需求侧的电量电价弹性矩阵，衡量需求侧受电价驱动的程度，并作为计算基础，对博弈模型中双方达成的一种电量和电价均衡状态进行定量计算。

需求侧用户对电价的反映情况可以用电量电价弹性矩阵来描述，该矩阵的理论基础为电量电价弹性，即电量变化率与电价变化率的比值[7]，如式（1）和（2）所示。式（1）表示电量电价的自弹性系数，式（2）表示电量电价的交叉弹性系数。

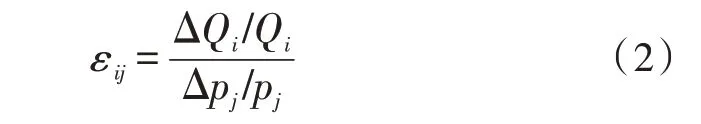
其中，i和j表示不同的时点，Qi表示i时点测得的对应时段的用电量，ΔQi表示由于价格变动而引起的用电量的变化量，pi和pj分别代表i和j时点的电价，Δpi表示i时点的电价变化。

电力电价弹性矩阵如式（3）所示，由此可得实施峰平谷分时电价后需求侧各时段的用电需求量变化情况，如式（4）所示：

其中，E为电力电价弹性矩阵，n为电价划分时段数。

综上，实行分时电价后各时段的实际用电量可用式（5）求得：

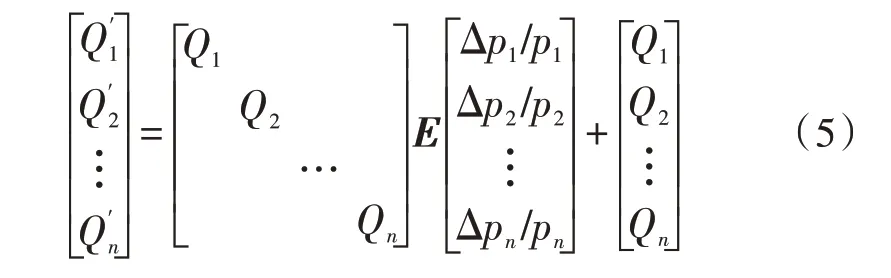
1.2 基于Stackelberg博弈法的光伏消纳模型

为对光伏消纳背景下用能侧各方参与的影响进行分析，基于式（1）～（5）的分析结果，首先对供给侧和需求侧分别建立目标函数。

对于供给方，其目标收益为售电收益减去购电成本。其目标函数计算公式为：

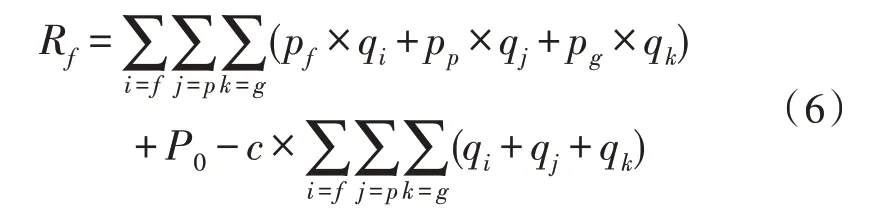
其中，pf、pp、pg分别为峰平谷时段的售电电价，P0为供给侧的光伏发电量收入，c为供给侧的单位购电成本。实际的qi、qj、qk受光伏出力情况的约束。

在电量消纳过程中，需求侧的收益函数即为购电成本的负值，该值的升高即表示购电的成本较少。其目标函数计算公式为：

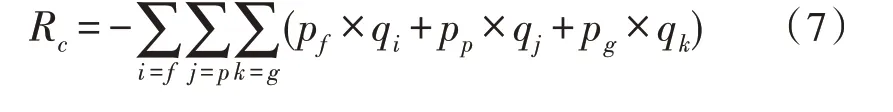
由式（6）与式（7）的目标函数计算公式可得，供给侧与需求侧的目标函数并不一致，因此该优化过程为多目标函数的优化过程。为对该光伏电量消纳过程中的多目标函数进行优化，引入Stackelberg 双寡头博弈模型，对该多目标函数进行转换。

根据纳什均衡的定义可得，市场主体交易决策的出发点均为自身收益最大化[8]。通过反复的博弈达到纳什均衡点时，任何一方市场参与者单方面改变策略均无法使其他参与者改变交易策略以获得更多的收益。在Stackelberg 双寡头模型中，要求参与方充分了解彼此的成本和市场需求情况[9-12]，在该模型中主要涉及两方参与者：领导者与追随者。Stackelberg 博弈法可用来分析存在不同行动次序对象的动态博弈，符合电力产业链中的行为情况。供给侧视需求侧在不同电价下的用电量为已知情况，进而调整其定价策略；需求侧视供给侧各时段的电量供应及电价水平已定，以调整自身生产情况中各用电时段的分配。该电力交易中的博弈主要来自双方均出于使自身利益最大化的目的进行购售电策略的选择。通过双方的博弈，达到各时段电量与电价的均衡状态，实现需求侧的用电优化[13]。

根据供给侧与需求侧的收益函数，考虑供给侧作为博弈中的追随者，需求侧作为博弈中的领导者的情况，即供给侧已知需求侧的历史负荷需求情况并能以此测算出其电量电价弹性的情形下，以供给侧利益最大化为目标，需求侧购电成本降低为约束条件的交易策略，利用Stackelberg 博弈法求取该模式下市场电力交易的最优解。由此，原多目标优化函数转换为单目标优化函数，其目标函数计算公式为：

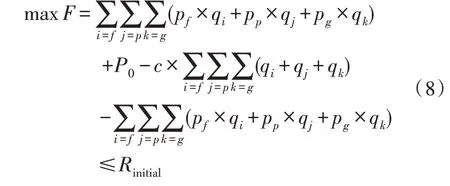
其中，Rinitial为优化前的原始值。

2 改进粒子群求解算法

式（8）的优化模型为非线性函数。为对该目标函数进行求解，应用了改进的粒子群算法[14]，求取Stackelberg 非合作博弈模型的纳什均衡解。

粒子群算法模型包括D维空间，N个粒子，其中，每个粒子主要由3 个变量定义，第i个粒子由3 个D维空间向量表征，分别为：

当前粒子位置：

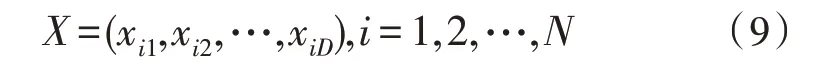
第i个粒子的飞行速度：

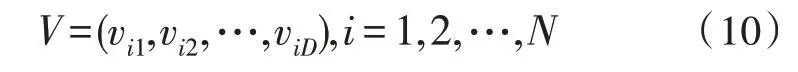
记录第i个粒子的历史最优位置：

记录搜索到的全局历史最优粒子位置：

对于每一个粒子，其D维速度及位置根据下式更新：

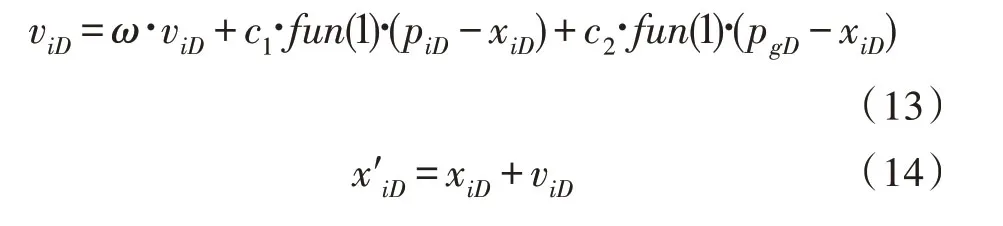
其中，ω为惯性权重，其决定了粒子先前的飞行速度对当前更新速度值的影响程度；c1和c2为粒子学习因子，通常取值为2；fun(1)为可以生成[0,1]范围内数值的随机函数。

此外，粒子的速度因求解问题的特殊性可以设定不同的范围[Vmin,Vmax]，即在执行速度按式（12）更新后，需对当前生成的下一时点的速度值进行取值的判断。

该文对目前已有的粒子群算法进行了部分改进，使得算法运行效率得以提高，且对最优解的求取有了更好的表现效果。主要改进处如下：

其中，gen为迭代次数，t为当前迭代代数。

此外，该文考虑到每个粒子产生变异的可能性，引入随机变异的部分粒子，以进一步优化算法，避免过早收敛的可能性[15]。

通过对粒子群算法中部分公式的改进，使得在算法搜索初期全局搜索权重较高，后期局部搜索权重较高，在一定程度上避免粒子群算法陷入局部最优的情况[16]。

利用改进的粒子群算法模拟供给侧与需求侧的博弈过程，通过迭代寻优，利用式（13）和（14）不断更新博弈过程中双方的最优选择，最终在解空间内求得当前约束条件下双方交易的最优策略。

综上，粒子群迭代求解算法的基本流程如图1所示。

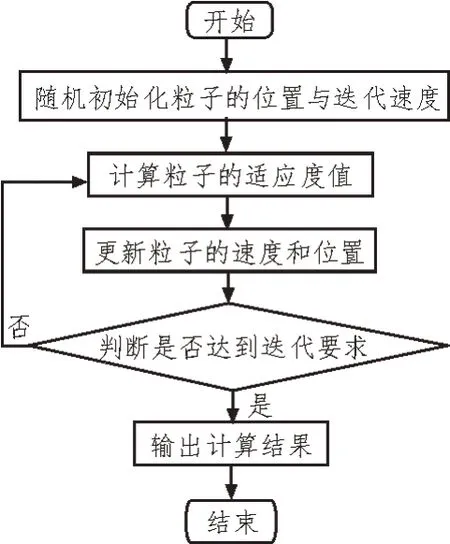
图1 粒子群迭代求解算法流程

3 算例分析

为验证模型的有效性，采用甘肃省某产业园的数据作为算例进行分析。在原运行条件下，产业园的峰平谷时段电价分别为0.656 4 元/kW·h、0.438 9 元/kW·h和0.221 5 元/kW·h。峰时段日均负荷为881.525 kW，平时段日均负荷为477.375 kW，谷时段日均负荷为1 073.3 kW。

利用前述优化的粒子群算法，求解供给侧和需求侧的电力交易模型，结果如图2 所示。最终求得最佳情况下供给侧的日收益为108.60 元，此时对应的峰平谷时段电价分别为0.787 7 元/kW·h、0.417 0 元/kW·h 和0.221 5 元/kW·h。

图2 粒子群优化算法结果

博弈前后的峰平谷电价情况，如表1 所示。

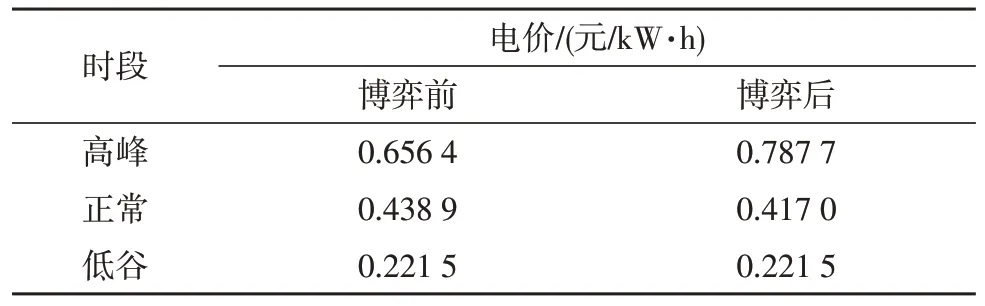
表1 博弈前后峰平谷时段电价对比

该模式下求得供给侧的收益为R=108.60 元/天；需求侧购电的平均电价为C=0.313 3 元/kW·h（原平均单位购电价为0.407 1 元/kW·h）

博弈前后的产业园峰平谷负荷分配情况，如表2所示。

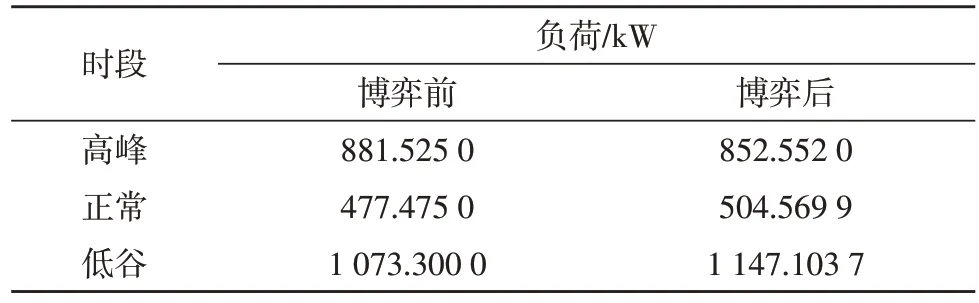
表2 博弈前后峰平谷时段日均负荷对比

由结果可知，峰谷拉开比由原来的0.821 3 变为0.743 2，降低了9.51%。峰时段日负荷也由原来的881.525 0 kW 变为852.552 0 kW，在一定程度上起到了削峰填谷的效果。

算例仿真结果表明，通过该模式可以优化需求侧的用电结构，在保证需求侧购电成本降低的前提下，实现供给侧效益最大化的效果。通过Stackelberg非合作博弈的模式，实现了需求侧和供给侧收益的共同提高，从而显著促进了光伏电量的消纳[17-18]。

4 结束语

该文针对目前存在的光伏就地消纳的问题，建立了光伏消纳背景下用能侧各参与方的优化模型。为分析实际光伏消纳过程中存在的多方收益均衡问题，模型中考虑了供给侧、需求侧的收益函数，解决了目前购售电端存在的信息不对称情况，并利用基于Stackelberg 博弈法的模型构建多方共赢的交易策略，以供给侧利益最大化，需求侧购电成本降低为模型约束条件，求解了双方最优交易策略。通过算例仿真分析，得出结论如下：

1）供给侧通过制定合适的电价策略，可以驱动需求侧改变用电习惯，从而一方面可以更好地匹配光伏出力情况；另一方面使得需求侧用电成本降低，通过这种模式实现供给侧收益最大化的效果。

2）通过供给侧与需求侧的博弈，不仅可以提高双方的目标收益，同时可以起到促进光伏消纳、削峰填谷的作用，显著提高了光伏消纳能力。

3）基于文中提出的采用Stackelberg 博弈法建立服务商与产业园间电力交易的博弈模型，后期可考虑引入区块链技术进行自动化、智能化的电力交易，使得各时点的电力交易更具针对性、高效性。