基于混合插值的机械升降臂控制系统设计

孙晓林，沈宏亮，杨立奎，曹新宇

（1.国网雄安新区供电公司，河北雄安 071600；2.国网河北省电力有限公司，河北石家庄 050000；3.国网河北电科院，河北石家庄 050000）

在机械制造领域中，随升降臂结构体所承担执行任务总量的增加，个别处置行为会出现明显的实用误差[1-2]。为避免上述情况的发生，传统轮式控制系统在寻迹闭环的支持下，直接计算与臂体相关的机械性控制指标，再联合转向定位算法，确定各项指标的实际作用范围[3]。但该系统很难完全抑制非合理升降指令的产生，易导致实控误差结果的不断增大。

混合差值可用来填充因图像变换而产生的像素空隙，在离散数据的支持下，该项应用理论可在非关联信息参量中插入多个连续函数，从而使得既定连续曲线能够全部通过给定的离散型数据节点。所谓差值是使数值计算结果无限逼近离散函数的处理方法，随着函数点取值理论的实施，差值计算量可在其他应用位置处对各个节点的近似数值结果进行初步估计，从而使各个像素空隙得到填充与弥补。

因此，为解决传统控制系统存在的不足，基于混合插值设计了一种新的机械升降臂控制系统，在电动升降器、控制传感器等多个硬件执行设备的支持下，确定最终的升降臂运动姿态行为。

1 机械升降臂控制系统硬件设计

机械升降臂控制系统硬件执行环境由混合型机械驱动电路、电动升降器、控制传感器三部分共同组成，具体搭建方法如下。

1.1 混合型机械驱动电路

混合型机械驱动电路如图1 所示。

图1 混合型机械驱动电路

图1 中，混合型机械驱动电路包含一个VSS 输入端、一个PWM 输入端和一个末位电量输出端，可在R1、R2、C1、C2等多个应用电阻设备的作用下，实现对控制系统内传输电子量的定向调度与处理。VSS 输入端、PWM 输入端分别与电网高压与低压端相连，可在承接交流传输电子的同时，建立与下级电阻设备之间的连接[4]。R1、R2是两个串联的执行电阻，在变阻器Q1的作用下，这两个阻值设备可直接感知C1、C2电容内的电子变动行为，并适当控制电路内的电子传输流量，从而满足D1、D2 设备的实际用电需求。

1.2 电动升降器

电动升降器可接收混合型机械驱动电路中的传输电子，并将其直接转化为变频输出电流。驱动电机负载机械电路的输出导线，并在减速器装置的作用下，实现对主动臂与从动臂元件的定向化调度[5-6]。

电动升降器结构如图2 所示。图2 中，托架位于电动升降器模块顶端，可巩固驱动电机、减速器等设备结构体之间连接的稳定性，从而使机械升降臂的运动行为逐渐趋于流畅。主动臂、从动臂之间始终保持相对稳定的连接附属关系，当驱动电机的输出行为发生改变时，主动臂会出现明显的运动趋势，此时从动臂也会随之产生小幅度的摆动[7-8]。

图2 电动升降器结构图

1.3 控制传感器

控制传感器结构如图3 所示。

图3 控制传感器结构图

图3 中，控制传感器以滤波放大器作为核心搭建装置，可在R3、R4、R53 个定值电阻的作用下，调节机械升降臂结构体内的控制电流与控制电压，从而使系统内部的电量应用需求得到充分满足。R6变阻器位于控制传感器上端，可根据R3、R4、R5电阻的实际情况接入阻值，控制元件两端的电压负载量，在传感器元件内传输电流保持稳定的情况下，随变阻器两端应用电压负载实值的提升，核心主机对机械臂升降行为的控制精度也开始出现逐渐下降的变化趋势[9-10]。GND 设备位于R5电阻下端，直接与控制电流输出端相连，可整合传感器元件内的所有应用电子量，并将其以交变电流的形式，传输至下级系统应用结构体之中。

2 机械升降臂控制系统软件设计

在各项硬件设备元件的支持下，按照升降臂空间位置表示、控制节点初始化、运动姿态定义的处理流程，搭建系统的软件执行环境，两相结合实现基于混合插值机械升降臂控制系统的顺利应用。

2.1 升降臂空间位置表示

升降臂空间位置描述了机械控制系统的平均运动范围，在不考虑其他外界干扰条件的情况下，受到机械臂升降速度、臂摆转动角度两项物理量的直接影响[11-12]。机械臂升降速度常表示为，在既定控制时间内，该项物理量的实际值相对稳定，不受除控制周期 |T|外其他物理量的影响。臂摆转动角度常表示为β，在混合差值原理的作用下，该项物理量的实际值始终小于最大转动角度βmax。联立上述物理量，可将升降臂的运动空间位置表示为：

其中，y代表差值应用常量，p代表与机械升降臂相关的混合理论应用系数。

2.2 控制节点初始化

控制节点初始化以控制软件复位作为起始处理环节，在混合差值原理的支持下，可对机械升降臂体表面的各项应用系数参量进行初步的定义与度量。当CAN 控制总线的波特率数值保持不变时，机械升降臂的运动范围会始终处于额定范围区间内；而随着运动控制时间的延长，CAN 总线的波特率数值会出现明显提升的变化趋势，直至将所有混合差值参量完全与待处置节点匹配起来[13-14]。当电动升降器的执行参数恢复至原始状态后，各项初始参数的指标水平才会逐渐达到理想化的数值标准。

控制节点初始化原理如图4 所示。

图4 控制节点初始化原理

2.3 运动姿态定义

运动姿态定义是基于混合插值机械升降臂控制系统设计的末尾处理环节，可联合多项物理应用系数确定系统的实际控制能力，从而实现对机械臂升降行为偏差的有效避免[15-16]。设λ代表与机械升降臂相关的位姿运动系数，规定在下限运动极值和上限运动极值之间，该项物理量不会出现明显上升或下降的变化趋势，而始终与升降臂控制权限均值保持相同的变化状态。在上述物理量的支持下，联立式（1），可将基于混合差值原理的机械升降臂运动姿态定义为：

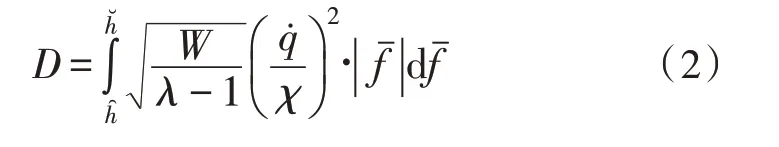
其中，χ代表既定的机械臂升降周期频度系数，代表与混合差值原理相关的臂体控制参量。至此，实现各项软、硬件执行环境的搭建，在混合差值原理的支持下，完成新型机械升降臂控制系统设计。

3 系统应用能力检测

为验证基于混合插值机械升降臂控制系统的实际应用价值，设计如下对比实验。选取一个执行能力相对稳定的机械升降臂结构体作为实验对象，当臂身得到完全伸展时，记录各项实验指标的具体数值。实验组主机搭载基于混合插值的机械升降臂控制系统，对照组主机搭载传统轮式控制系统。实验所用机械升降臂结构如图5 所示。

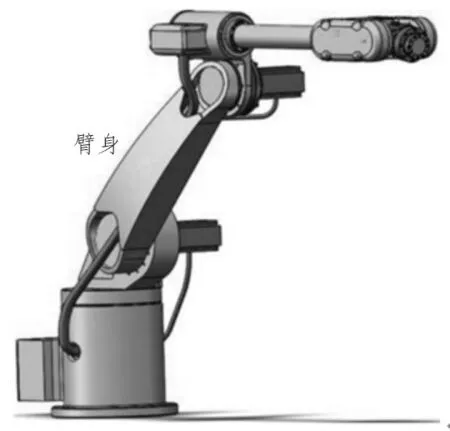
图5 机械升降臂结构体

IUD 指标能够反映系统对机械臂升降行为的实控误差水平，通常情况下，指标数值越大，实控误差也就越大，反之则越小。表1 记录了实验组、对照组IUD 指标的具体变化情况。

表1 机械臂升降行为的实控误差对比表

分析表1 可知，理想状态下与机械臂升降行为相关的IUD 指标数值始终保持不变。实验组IUD 指标则在小幅上升后，开始持续下降，全局最大值仅达到19%，与初始极值相比，下降了26%。对照组IUD指标在小幅上升后，开始趋于稳定，全局最大值达到49%，与实验组极值相比，上升了30%。综上可知，随着基于混合插值机械升降臂控制系统的应用，IUD指标确实出现了明显下降的变化趋势，可从根本上解决核心主机对机械臂升降行为的实控误差水平过高的问题。

LEA 指标能够描述系统非合理升降指令的产生数量，一般情况下，LEA 指标数值越大，系统产生的非合理升降指令数量也就越多，反之则越少。表2记录了实验组、对照组LEA 指标的实际变化情况。

表2 非合理升降指令的数量对比表

分析表2 可知，理想状态下与非合理升降指令生产数量相关的LEA 指标数值始终保持不变。实验组LEA 指标在一段时间的稳定状态后，开始出现持续性下降的变化趋势，从第40 min 开始，又开始逐渐趋于稳定，全局最大值仅达到33%，与初始数值相比，下降了21%。对照组LEA 指标则保持先上升、再稳定、最后不断下降的变化趋势，全局最大值达到56%，与实验组极值相比，上升了23%。综上可知，随着基于混合插值机械升降臂控制系统的应用，LEA 指标也出现了明显下降的变化趋势，满足系统主机有效控制非合理升降指令产生数量的实际应用需求。

4 结束语

与传统轮式控制系统相比，基于混合插值机械升降臂控制系统可在混合型机械驱动电路、电动升降器等多个硬件设备结构体的作用下，实现对升降臂臂身运动姿态的精准定义，且可在完成控制节点初始化的同时，得到明确的升降臂空间位置表示结果。从实用性角度来看，IUD 指标、LEA 指标的快速下降，可解决核心主机对机械臂升降行为实控误差水平过高的问题，在精准化控制方面，可使臂体结构的基本应用需求得到有效满足。