基于M-Rife算法的梯形波FMCW雷达多目标检测技术研究

崔英杰，刘云学，宋健强，焦浩

（烟台大学光电信息科学技术学院，山东烟台 264005）

线性调频连续波(LFMCW)雷达具有测距精度高、分辨率高、结构简单和体积小等优点，近年来在军用领域和民用领域得到了广泛应用[1-2]。传统的LFMCW 雷达有锯齿波调制与对称三角波调制两种频率调制方式[2]。锯齿波调制方式存在距离速度耦合问题，对称三角波调制方式虽然能通过上下扫频差拍回波信号中心频率解距离-速度耦合，但在多目标情况下，又存在上下扫频频谱配对的问题。

文献[3-6]通过将线性调频连续波与恒频连续波相结合，提出了许多三角波与恒频连续波组合的发射波形。这些波形原理基本相同，都是通过恒定频率段测得目标速度再与上下扫频段配对得到的目标进行匹配，去除虚假目标。恒频段测速精度成为多目标配对的关键，如果恒频段测得目标速度不够准确，就有可能与虚假目标配对，形成错误配对从而漏掉真实目标。

考虑到实现的复杂度，虽然有很多恒频段测频方法[7-10]，工程中通常采用快速傅里叶变换(FFT)分析LFMCW 雷达差拍回波信号的频谱，估计信号的频率。但由于FFT 存在频谱泄露和栅栏效应，当频谱实际峰值谱线与FFT 的谱线不重合时，就会产生较大的频率误差[11]。在FFT 变换的基础上，采用MRife 算法[12]来进行频率估计，既提高频率估计的精度，增大的计算量又非常有限，从而提高了测速的精度，降低了与虚假目标配对的可能性，也就提高了梯形波FMCW 雷达的多目标检测能力。

1 梯形波基本原理

1.1 梯形波恒定频率段测速原理

将雷达发射信号和回波信号经过混频器混频，就得到差拍回波信号，对差拍回波信号进行频谱分析就可以得到目标的距离和速度信息。梯形波调频连续波信号包含上下扫频段和恒定频率段，其雷达工作原理如图1 所示，图中实线为雷达发射信号，虚线为回波信号，发射信号与回波信号形状相同，时间相差2(R+vt)/c，R为目标距离，v为目标速度，c为光速，f(t)为梯形波信号，fIF(t) 为差拍回波信号。

图1 梯形波LFMCW雷达原理图

下面对恒定频率段的测速原理进行分析，对于恒定频率段t∈[T,2T]，雷达发射信号为：

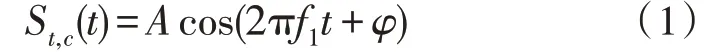
雷达接收到的回波信号为：

其中A为振幅，f1为恒频段频率，Kr为反射系数，τ(t)为延时函数，φ为随机初相，φ为目标反射后引起的相位变化。

将St,c(t)和Sr.c(t)混频，得到差拍回波信号：

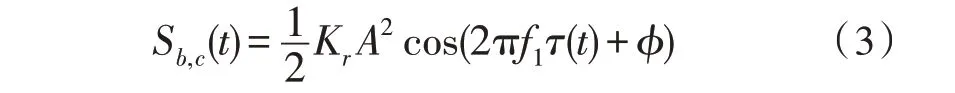
将上式进行正交复变换得：

将上式作傅里叶变换得：

由式（6）可以看出，恒定频率段的差拍回波信号频谱幅度峰值处中心频率为：

中心频率只包含目标的速度信息，所以通过恒频段可得到目标的速度。由上式可得目标的速度为：

显然恒定频率段测速精度取决于频率fb,c的估计精度。

1.2 梯形波多目标配对原理

在多目标情况下，梯形波上下扫频段频谱图中会出现多个峰值，这就面临上下扫频目标配对问题[13]。恒定频率段由于未经过调制可直接测得目标的速度信息，通过恒频段测得的目标速度与上下扫频解距离-速度耦合得到的速度进行配对，这样可望排除虚假目标得到真实目标。在理想情况下，可以通过该方法配对得到正确的目标。当恒频段测得的目标速度存在误差且真实目标速度与虚假目标的速度很接近时就很容易错配[14]，而通过M-Rife 算法测得目标速度更加准确，能够防止虚假目标与正确目标进行配对，如图2 所示。

图2 目标正确配对与错误配对

2 算法分析

2.1 Rife算法

Rife 算法[15]通过对信号幅度频谱最大谱线和相邻次最大谱线进行插值来进行频率的估计。

假设信号经过FFT 之后，最大谱线出现在k0处，通过Rife 算法得到的频率估计值为：

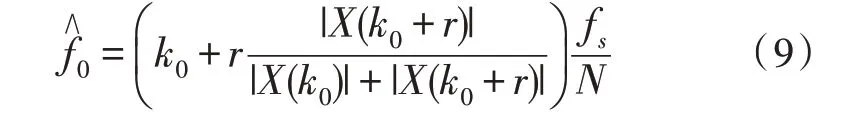
其中，fs为采样频率，N为采样点数，|X(k0)|为最大谱线值，|X(k0+r)| 为相邻次最大谱线值，当|X(k0+1)|≥|X(k0-1)|时，r=1，当X(k0+1)|＜|X(k0-1)|时，r=-1。

2.2 M-Rife算法

有噪声干扰情况下，当信号频率位于离散傅里叶变换(DFT)量化频率点附近时，Rife算法误差较大[12]，为了改善量化频率点附近频率估计误差较大这一缺陷，文献[12]中提出了M-Rife 算法。

针对Rife 算法当估计的频率位于两个相邻量化点频率中心区域估计精度高这一特点，M-Rife 算法主要通过信号序列的移位减小频率估计的误差。M-Rife 算法思想：先执行一次Rife 算法，若估计到的频率值在两个相邻量化频率点的中心区域时则算法停止；若估计到的频率值接近量化频率点，则信号序列移位Δf/3(Δf=Fs/M)，Fs为采样频率，M为FFT 点数，然后重新执行一次Rife 算法以得到频率的精确估计[16]。M-Rife 算法测速流程如图3 所示。

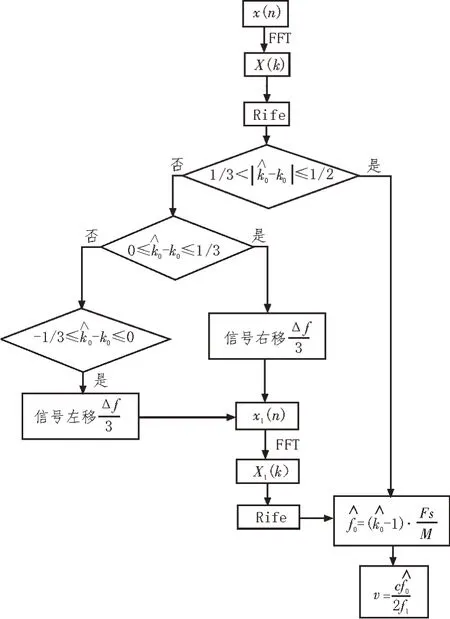
图3 M-Rife算法测速流程图

文中研究的M-Rife 测速法步骤如下：

1）对梯形波恒频段差拍回波信号x(n) 作M点FFT 得X(k)。

2）由FFT 得到频谱峰值最大值对应的FFT 点数k0，由Rife 算法得到的频谱峰值的最大值对应的FFT点数为，计算Δk=-k0。

3）若1/3 ＜|Δk|≤1/2，直接计算频率估计值，再由式（8）求得速度测量值。

4）若0 ≤Δk≤1/3，信号右移Δf/3 得到x1(n)，将x1(n)进行FFT，再经过一次Rife 算法，计算频率估计值，再由式(8)求得速度测量值。若-1/3 ≤Δk≤0，信号左移Δf/3 得到x1(n)，将x1(n) 进行FFT，再经过一次Rife 算法，计算频率估计值，再由式（8）求得速度测量值。

3 仿真分析

文中使用Matlab 进行仿真验证，设定系统仿真参数，如表1 所示。通过实验，采集了不同速度差拍回波信号的数据，分别利用FFT 算法、M-Rife 算法进行频率估计，并计算出相应的速度，进行多目标配对。

表1 系统仿真参数

信号的频率分辨率为Δf=fs/N=1 220.703 125 Hz，根据式（8）可得v=fb,c/520，故速度分辨率为Δv=Δf/52=2.347 506 m/s。选取一个目标，距离保持不变，加入信噪比(SNR)为-5 dB 的加性高斯白噪声进行仿真，表2 为速度在6.00～14.00 m/s 之间的仿真数据，图4 为不同速度测量误差的对比图。

表2 不同算法得到的速度(m/s)与理论速度(m/s)的对比

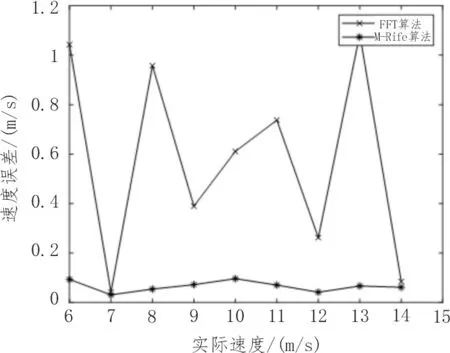
图4 速度测量误差对比

由表2 和图4 的误差曲线可以看出，该文采用的M-Rife 算法与FFT 算法相比，测速误差在整个速度段上都有明显的减小。由表2 中的数据可看出，在目标速度为13 m/s 时，FFT 算法的速度误差为1.0850 m/s，为整个速度段中误差最大的点。表3 为不同信噪比下的速度误差。

表3 不同信噪比下的速度误差(m/s)

由表3 可以看出，随着SNR 的增大，FFT 算法的测速误差不变，而M-Rife 算法的测速误差逐渐减小，并且M-Rife 算法的测速误差远小于FFT 算法。

以上仿真结果已经证明，与FFT 直接法相比，基于M-Rife 算法的恒频测速精度更高。下面对此测速算法在提高梯形波FMCW 雷达多目标检测能力方面进行仿真验证。设置3 组目标，分别包含速度距离都不同、部分目标速度相同距离不同、部分目标距离相同速度不同的，目标参数如表4 所示。加入SNR 为-5 dB 的加性高斯白噪声进行仿真，多目标配对结果分别如图5、图6、图7 所示。每个图中包含(a)、(b)、(c)、(d)4 个小图，图(a)和图(c)为用FFT 算法和M-Rife 算法恒频测速然后进行目标配对的图，图(b)和图(d)为目标配对的结果。

表4 目标参数

在图5 中，由FFT 算法在恒定频率段测的速度进行多目标配对得到4 个目标，通过与真实目标对比，其中有两个虚假目标。同样在图6 和图7 中，FFT 算法恒频测速进行多目标配对得到4 个目标中都有一个虚假目标。而通过M-Rife 算法恒频测速再进行多目标配对的3 组配对结果都为真实目标。由以上目标配对结果可以看出，由FFT 算法恒频测速再进行目标配对都出现了目标错配的情况，得到的3 组目标中都存在虚假目标，而M-Rife 算法恒频测速再进行目标配对得到目标全部为真实目标。以上仿真实验结果表明，相比于FFT 算法，在相对复杂多目标环境中，用M-Rife 算法进行恒频测速然后进行多目标配对能够排除虚假目标而得到真实目标，其多目标检测能力更强。

图5 第一组目标配对结果

图6 第二组目标配对结果

图7 第三组目标配对结果

4 结论

该文研究了一种提高梯形波FMCW 雷达恒频段测速精度以改善多目标检测能力的方法，用M-Rife算法来估计梯形波恒频段差拍回波信号的频率。该算法与FFT 直接法相比，虽然增加了少量运算量，但显著提高了频率估计的精度，从而提高了测速的精度。仿真结果表明，在进行多目标检测时，当恒频段采用了M-Rife 算法进行频率估计后，梯形波FMCW雷达多目标检测能力提高很明显。该算法易于实现，可应用于梯形波FMCW 雷达多目标检测系统。