基于分数阶微积分的图像去噪算法研究

徐艳华

（陕西铁路工程职业技术学院，陕西渭南 714000）

目前，分数阶微积分在科学、工程等众多领域得到了迅速的发展，因此任意阶微分方程在物理、流体力学、生理学、工程、势理论、弹性力学等领域得到了广泛的研究[1-2]。近年来，将微积分应用于图像处理已成为一个热点研究课题，并有大量的研究成果发布[3]。与整数阶微积分相比，在图像去噪过程中，分数阶微积分方法可以在保留平滑区域细节信息的同时增强边缘，使纹理更加清晰。

传统的分数阶微积分方法对图像边缘、纹理和平滑区域采用相同的阶数处理。当使用高分数阶来处理图像噪声时，弱纹理和平滑区域将被忽略，而使用低分数阶会削弱图像的边缘[4]。因此在实际应用中，仅使用整数分数阶微积分对图像的去噪效果并不理想，进而提出了基于分数阶微积分的图像去噪算法。该算法利用图像梯度特征构造分数阶微积分算子，采用不同的分数阶对不同的像素进行处理，从而实现图像去噪[5]。

1 分数阶微积分理论分析

1.1 分数阶微积分

根据傅里叶变换的基本理论，将图像信号处理定义为：

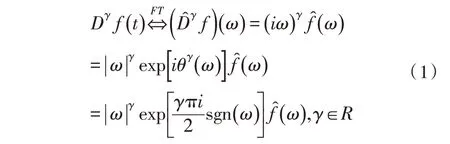
式 中，Dγ为γ阶微分算子，ω为角频率，为分数阶微积分滤波器的滤波函数，sgn(∙)表示整数部分的数字符号。

在频率特性方面，分数阶微积分利用Gamma 函数Γ(t)t将其定义扩展到分数阶，Grumwald-Letnikov（GL）定义的γ阶分数阶微积分为：

式中，[∙]表示整数部分，信号的持续时间f(t)为[a,t]，a是任意实数，表示由GL 定义的γ阶分数微积分算子。当γ＞0 时，是γ阶的分数微分算子；当γ＜0 时，是γ阶的分数积分算子。

分数阶微积分的频率响应如图1 所示。

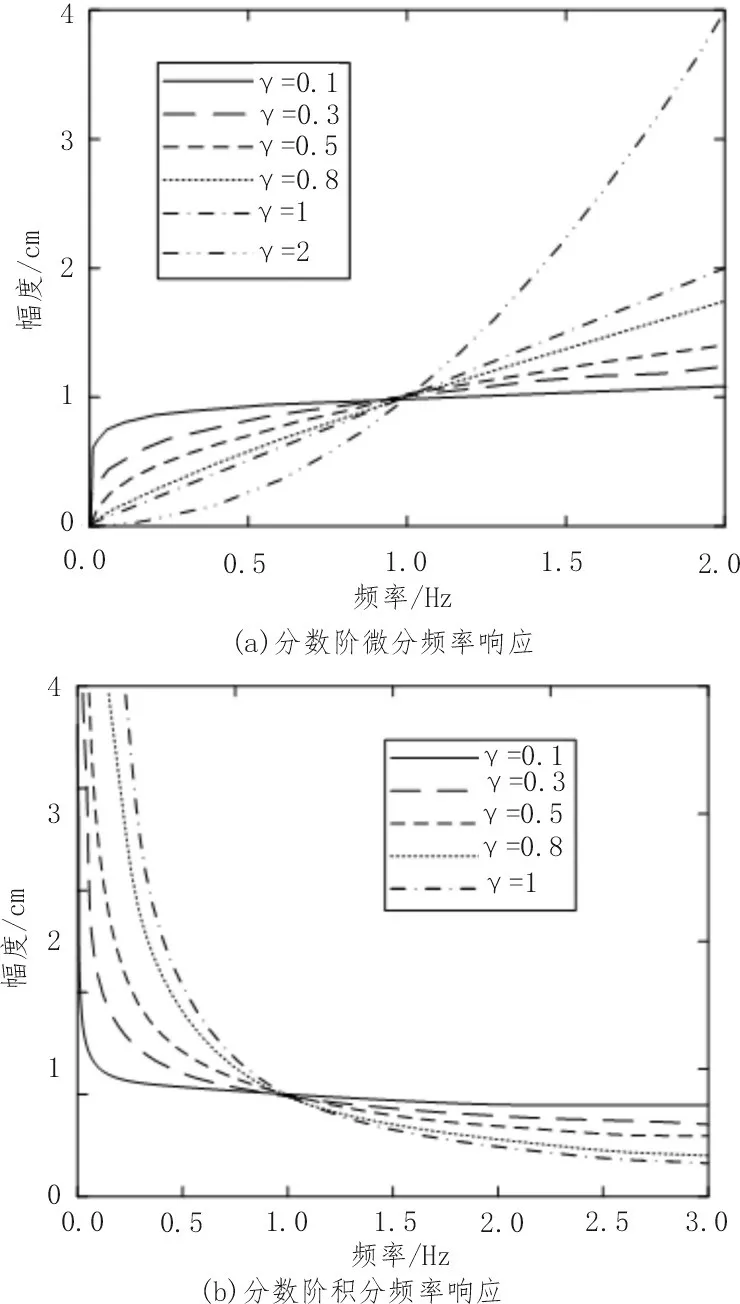
图1 分数阶积分的幅频特性曲线

由图1（a）可知，随着分数阶微分阶次和频率的增加，对于高频信号的增强作用也明显增加，且增强的幅度在后期最为明显。由图1（b）可知，随着分数阶积分阶次和频率的增加，分数阶积分运算对高频信号的衰减幅度也逐渐增加。

由此可知，分数阶微分可增强、保留图像边缘和纹理特征，而分数阶积分则可以去除图像噪声。

1.2 分数阶微积分对图像的处理

在二维数字图像中，相邻两个像素之间是灰度变化的最短距离，因此图像在x轴和y轴方向上的持续时间只能以像素为单位来测量[6]。因此根据GL 分数阶微积分表达式，可以得到信号f(t)的γ阶为：

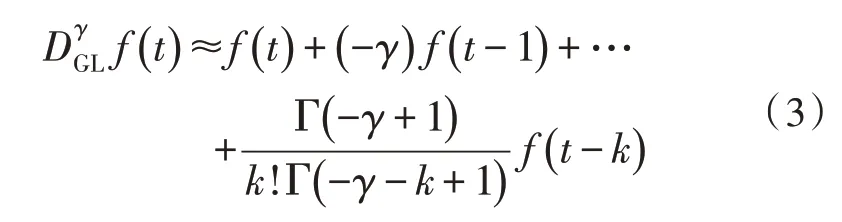
根据信号f(t)的γ阶分数积分表达式，对于任何函数f(x,y)∈L2(R2)，求出γ阶偏微积分关于x和y的微分表达式，因此可得到5×5 分数积分掩模，如图2 所示。

图2 分数积分掩模

掩模是在8 个方向上叠加部分分数阶积分得到的，是旋转不变的。式中，w1、w2和w3分别为第一、第二和第三系数，且w1=1、w2=-γ、w3=(-γ)(-γ+1)/2。此时，通过考虑该掩模卷积的空域滤波，可以得到用γ阶分数积分处理的图像。

2 图像去噪算法

2.1 噪声类型

在图像中，各类别的噪声一般划分成两种典型的噪声：椒盐噪声和高斯噪声[7]。

椒盐噪声由不完善的开关设备产生，通常产生于图像传感器、解码处理或图像切割等[8-9]。该噪声出现位置为随机位置，但幅值基本相同。

对于图像的每一个像素点，均存在高斯噪声，其概率密度函数为：

其中，z为灰度值，u为期望值，σ为标准偏差，σ2为方差。

2.2 噪声判别

图像边缘和纹理丰富区域的梯度较大，平滑区域的梯度较小[10-11]。图像u0(x,y)的像素(x,y)处的梯度可表示为。梯度模值公式为：

图像的边缘是连续的，据此构造出噪声边缘的判别函数：

式中，|∇Vx,y|与|∇′Vx,y|分别是中间和附近区域像素点的梯度模值。

2.3 基于分数阶微积分的图像去噪

在图像去噪过程中，需要将噪声点与纹理区域区分开[12-13]。将图像出现噪声点作为一个小概率事件，结合局部特征来分割各个区域，并使用3×3 区域来分析图像结构信息。

最小绝对灰度距离为：

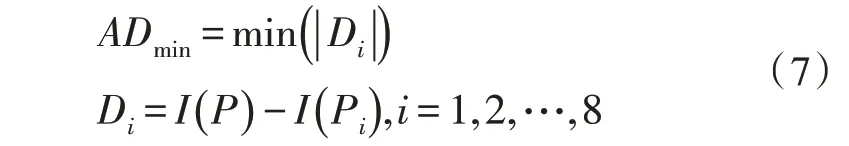
式中，I(P)是像素P的灰度值，P和Pi是像素。

在图像的8 个方向上，图像边缘多为连续像素[14-15]，因此最小绝对距离ADmin较小。假设当前像素u0(x,y)中，8 个方向上每个方向的灰度距离平均值为M(x,y)，则：

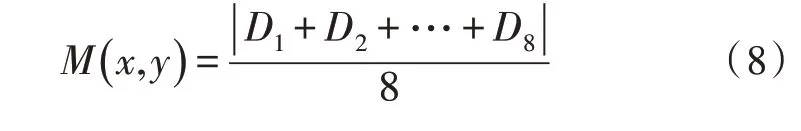
选择分割后的噪声点最小值M(x,y)作为图像噪声点的阈值T。当M(x,y)≥T时，将对应的像素(x,y)视为噪声点，该值越大，噪声越强。在图像去噪过程中，应将阶数γ取为负值，且阶数的大小与M(x,y)的值有关[16]。通过选择一个自适应分数阶，当噪声较大时，自适应积分阶数将变小、灰度幅值将衰减。

当1 ＜M(x,y)＜T时，对应的像素(x,y)被视为边缘或纹理区域的一个点，在去噪过程中分数阶微分阶数应取正值。阶数的大小与M(x,y)和计算熵EN(x,y)有关，则通过选择一个自适应分数阶。

当0 ≤M(x,y)＜1 时，将像素(x,y)视为平滑区域中灰度值不变的一点。

3 实验结果及分析

基于Matlab R2012a 软件对所提算法进行仿真实验，其中计算机的硬件配置：CPU 为2.40 GHz Intel Core i7，RAM 容量为4 GB。

对于一种图像去噪算法，通常采用峰值信噪比（PSNR）来评价去噪效果及其综合性能。PSNR 值越大，算法的去噪效果越优。峰值信噪比定义为：

式中，原始图像的大小为M×N，u0(i,j)表示原始图像，un(i,j)表示去噪后的图像。

3.1 可视化分析

实验中使用的图像大小为256×256，具有不同纹理的莉娜和船舶图像。设定λ1=0.4、λ2=0.6，取噪声平均值作为实验噪声强度。将所提算法与文献[9]、文献[10]、文献[12]中去噪算法得到的图像进行可视化对比，结果如图3、图4 所示。

图3 不同算法对含噪莉娜图像的去噪效果

图4 不同算法对含噪船舶图像的去噪效果

从图3 和图4 中可以看出，文献[9]采用迭代空间屏蔽的去噪方法，对于椒盐和高斯噪声的去噪效果不理想；文献[10]在保持图像边缘细节方面表现较好，但在去噪效果上仍有所欠缺；文献[12]在消除所有噪声的同时也丢失了图像中大量的细节信息，图像的边缘和细节纹理区域产生了模糊化，去噪效果有待提高。传统的顺序使图像模糊，同时使图像亮度降低。而所提算法去噪后的图像，既能较好地去除噪声，又保持了帽檐等边缘细节信息[17-18]。

3.2 去噪效果定量分析

此外，对所提算法的去噪性能进行定量分析。4种不同算法的PSNR 比较结果如表1 所示。

表1 各噪声图像经算法处理后的PSNR

从表1 中可以看出，不论是对椒盐噪声还是高斯噪声，所提算法的PSNR 均高于其他对比算法，分别为30.470和25.653。文献[9]由于依赖于空间信息，因此去噪效果不理想；文献[10]利用改进的曲率滤波进行图像去噪；而文献[12]在此基础上结合了小波变换，因此去噪效果有所增强，分别是25.566和24.462。

4 结束语

该文提出一种基于分数阶微积分的图像去噪算法。基于分数阶微积分对图像处理进行了理论分析，结合局部结构划分噪声点、边缘、纹理区域和平滑区域构造了一个分段函数，以实现对不同区域像素的去噪处理。此外，基于Matlab 仿真平台对所提算法进行实验论证。结果表明，所提算法PSNR 均高于其他对比算法，在椒盐噪声和高斯噪声中PSNR 的值分别为30.470 和25.653，且能在去除噪声的同时保持图像边缘和纹理特征。在后续研究中，将聚焦解决如何与其他的一些经典去噪算法相结合以得到更优的去噪效果。