民机概念设计阶段的气动弹性优化设计*

吕继航 杨何发

（中航通飞华南飞机工业有限公司，珠海 519040）

引言

气动弹性是研究飞行器在相对气流中、气动力和弹性力相互作用下的力学行为的一门学科，在现代飞机设计过程中占有相当重要的地位［1］.考虑气动弹性问题时，主要是设计合理、可行的刚度分布，因此刚度设计成为结构设计的首要任务，也是后续设计的重要依据.飞机设计过程中，常常需要进行结构再设计，以满足气动弹性稳定性要求［2］.

以往，飞机的气动设计和结构设计都是串行开展的，通常采用刚性飞机进行气动外形初始设计，然后根据气动外形进行载荷和结构设计.这种传统的设计方法存在很多不足，尤其对于速度高、柔性大的飞机，难以保证结构设计满足气动弹性稳定性要求，有时要进行飞行包线的限制，有时更要付出部分结构重量的代价.特别是在飞机概念设计阶段，结构刚度设计需要的很多信息需要通过并行或后续设计才能得到，导致结构方案可行性论证不足，在后续设计中需要进行结构刚度的设计更改甚至重新设计，由此造成人力、周期的成本增加.

随着优化技术的发展，可以采用优化方法进行飞机结构再设计，它能以最小的设计代价获得期望的气动弹性性能［3］.如当飞机气动弹性要求无法满足时，可以进行结构优化，以改善这些气动弹性问题；又如，在提高飞机其它特性时，为使气动弹性特性在期望范围内，可以进行满足气动弹性约束的结构优化设计；甚至，当气动弹性及其它特性都满足要求时，也可以进行飞机结构优化设计，以进一步减轻结构重量，改善飞机总体性能.

本文根据民机概念设计阶段、气动弹性稳定性的设计需要，以某大展弦比机翼为例，按照给定的气动外形进行气动建模，并参照同类飞机刚度数据进行结构建模，然后以结构重量最小化为优化目标，以颤振速度、强度、刚度、发散速度的限制为约束条件，利用优化迭代方法开展气动弹性优化设计，以期给出满足颤振、强度、刚度以及发散约束的机翼刚度分布，为后续结构设计提供参考.

1 基本理论

1.1 颤振运动方程

根据拉格朗日方程，升力面的颤振运动一般可以描述为：

式中，q为广义坐标，M、C、K分别为广义质量矩阵、广义阻尼矩阵和广义刚度矩阵；QA为广义非定常气动力矩阵.工程应用中，一般认为颤振临界状态下，升力面作简谐振荡运动.忽略非定常气动力的非线性，则颤振运动方程转化为线性方程，如下式所示：

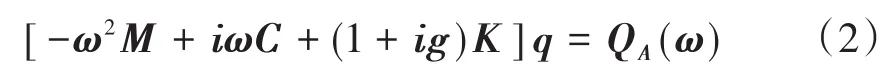
式中，ω为结构固有频率，g为结构阻尼系数.为了便于求解，将公式（2）转化为状态空间形式，则颤振问题就转化为运动方程的线性特征值问题［4］：

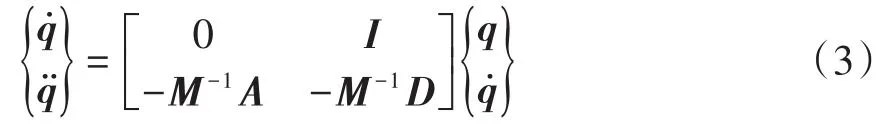
式中，I为单位矩阵，A、D分别为系数矩阵.采用pk法或g法求解状态空间运动方程，根据特征值计算气动弹性系统的频率、阻尼，即可得到升力面的颤振特性.

1.2 结构刚度预估

动力学分析主要关注飞机的总体特性，故而可以在静力学模型的基础上做适当简化.对于大展弦比飞机，可以采用梁单元进行结构建模.其中，梁单元的刚度数据是结构动力学建模的基础.概念设计阶段，对于飞机的刚度分布可以进行预估［5］.如有原型机，则可借鉴原型机的刚度数据进行新机的刚度预估.若无原型机，也可以按照工程经验公式建立新机与参考飞机之间的刚度换算关系，计算新机初步的结构刚度数据：

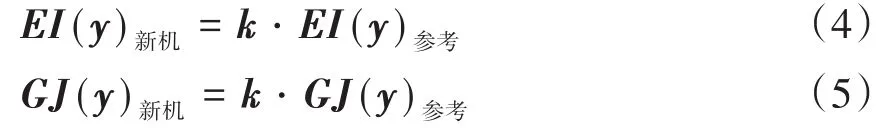
式中，EI为弯曲刚度，GJ为扭转刚度，y为站位坐标，k为比例系数.

式中，Mb为结构各站位的弯矩.对于飞机的弯矩分布，在没有详细的输入参数时，可以采用工程方法进行估算.弯矩主要由气动载荷、惯性载荷两部分组成，但惯性载荷与飞机的质量分布有关，在概念设计阶段通常很难得到.相对而言，根据概念设计方案比较容易得到机翼的气动载荷，可以用于评估飞机的总体载荷特性.

机翼的气动载荷估算时，假设气动力沿翼面展向均匀分布，翼根的气动力最大，翼尖的气动力为零，则根据平衡关系，在翼面的每一个展向站位，其气动力可以描述为［6］：

对应的气动弯矩则为：

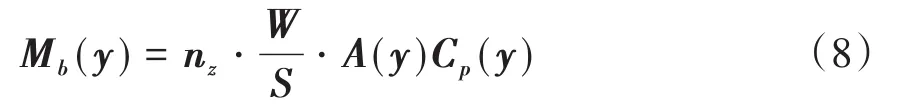
式中，nz为飞机的法向限制过载系数，W为飞机总重量，S为机翼的浸润面积，A（y）为y站位外侧的翼面面积，Cp为翼面压心距翼根的距离.对于椭圆形机翼，各站位处的翼面面积可以按下式计算：

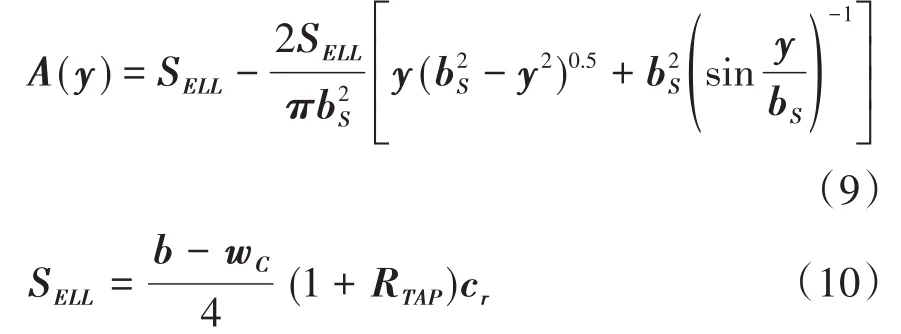
式中，bs为机翼的半翼展，b为全翼展，wc为翼身整流区宽度，RTAP为梢根比，cr为根弦长.翼面压心的展向距离为：

1.3 优化设计模型

优化设计问题实际上是一个约束极值问题，是指对于某一个物理系统，求解一组设计变量y（n）和极小化目标函数F（y），使其同时满足给定的约束条件，数学上一般将其描述为［7］：

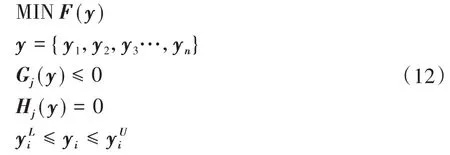
由式（12）可知，优化设计问题主要包括三个要素，即设计变量、目标函数及约束条件.其中，设计变量是表征设计状态的一组可选参数；目标函数则是要被极小化的标量函数，是设计变量的函数，其提供了评价设计质量优劣的标准；约束条件是对设计参数的边界限制，从而使结构响应限制在允许的变化范围内.

通常，也需要对设计变量进行约束以限制参数优化范围，从而提高优化效率，同时避免出现不满足实际情况的伪设计.

2 优化建模

2.1 结构与气动建模

飞机气动弹性分析时，主要着眼于结构的总体特性，而不是细节特性，因此可对动力学模型进行适当简化.

以某大展弦比机翼为例，其结构模型如图1所示，边界条件为根部固支状态.其中，对于大展弦比翼面，翼根效应区及弦向变形相对较小，同时为了降低有限元阶数，将机翼简化为梁模型［8，9］.梁的弯曲刚度、扭转刚度参照同类飞机的刚度分布，并按照两者的气动弯矩进行了比例缩放.对于翼载燃油、设备等除结构以外的载重，其质量分布参照重量指标给定.此外，为了便于识别各阶模态的振动形态，将机翼几何外形的法向投影与梁模型连接在一起.当然，外形单元的刚度很小，不会对机翼的固有特性产生影响.

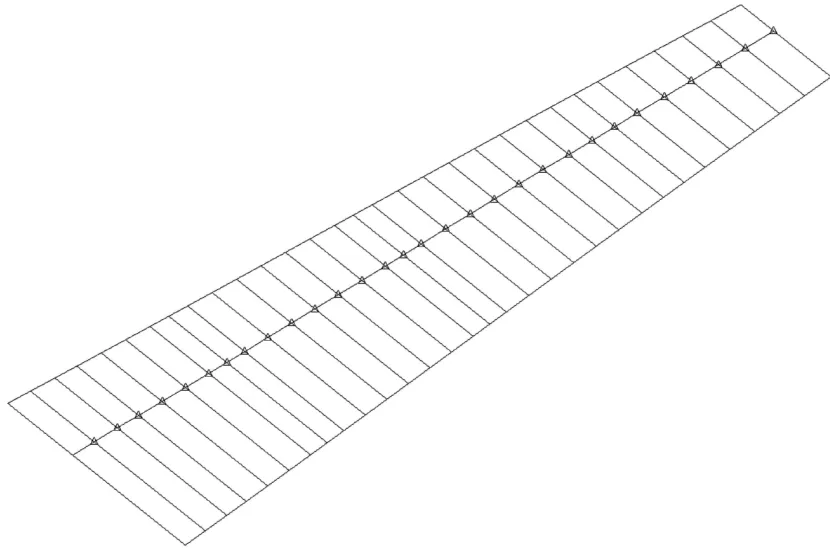
图1 翼面结构模型Fig.1 Structure model of wing

机翼的气动模型如图2所示.其中，按照给定的气动外形，忽略来流的三维效应，将机翼升力面划分为若干个梯形的气动网格，网格的纵列平行于来流方向，采用亚音速偶极子格网法进行非定常气动力计算［10］.

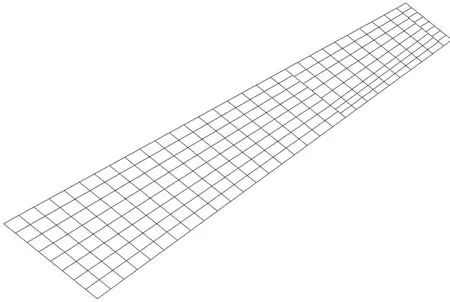
图2 翼面气动模型Fig.2 Aero model of wing

2.2 设计变量定义

根据飞机设计要求，气动弹性优化的目标为使机体结构重量最小化，同时满足强度、刚度、静气动弹性和动气动弹性等方面的要求［11］.气动弹性优化求解时，认为机翼几何外形初步确定，主要关注结构方面的设计参数.取机翼材料等效弹性模量E=71000MPa、G=27000MPa、材料密度ρ=2750kg/m3，然后以结构重量最小化为目标，对结构模型中梁单元的横截面积A、截面惯性矩I1、I2和极惯性矩J进行优化设计.

令yi为独立的设计变量，则梁单元的物理属性可表示为：

其中，a为变量的权重系数.式（13）描述了结构单元的物理属性与设计变量之间的一种依赖关系，但这里的设计变量并没有明确的物理意义，它与结构单元的物理属性相关.具体求解时，必须给定设计变量的初始值和取值范围.

2.3 设计约束定义

定义设计目标和设计变量后，还应定义模型优化的约束条件.对于机翼气动弹性优化问题，除要满足静气动弹性、动气动弹性的约束外，还要满足强度、刚度方面的要求，包括：

a）强度方面的约束：机翼根部的应力应在0.50～0.67倍许用值之间.

b）刚度方面的约束：翼尖相对于翼根的扭转角不超过2.5°.

c）静气动弹性方面的约束：机翼的发散速度不小于1.15vmax.

d）动气动弹性方面的约束主要是对颤振速度的约束.由于直接对颤振速度施加约束会对优化计算带来不便，因此将对颤振速度的约束转化为在给定的来流速度下对系统阻尼的约束，即要求在飞行包线内的典型来流速度下，有下式成立：

式中，δ为等效变量，γ为气动弹性系统的阻尼系数.可见，式（14）要求在给定的来流速度下，系统阻尼必须为负值，从而满足颤振稳定性要求.图3描述了民机概念设计阶段气动弹性优化设计的基本流程.

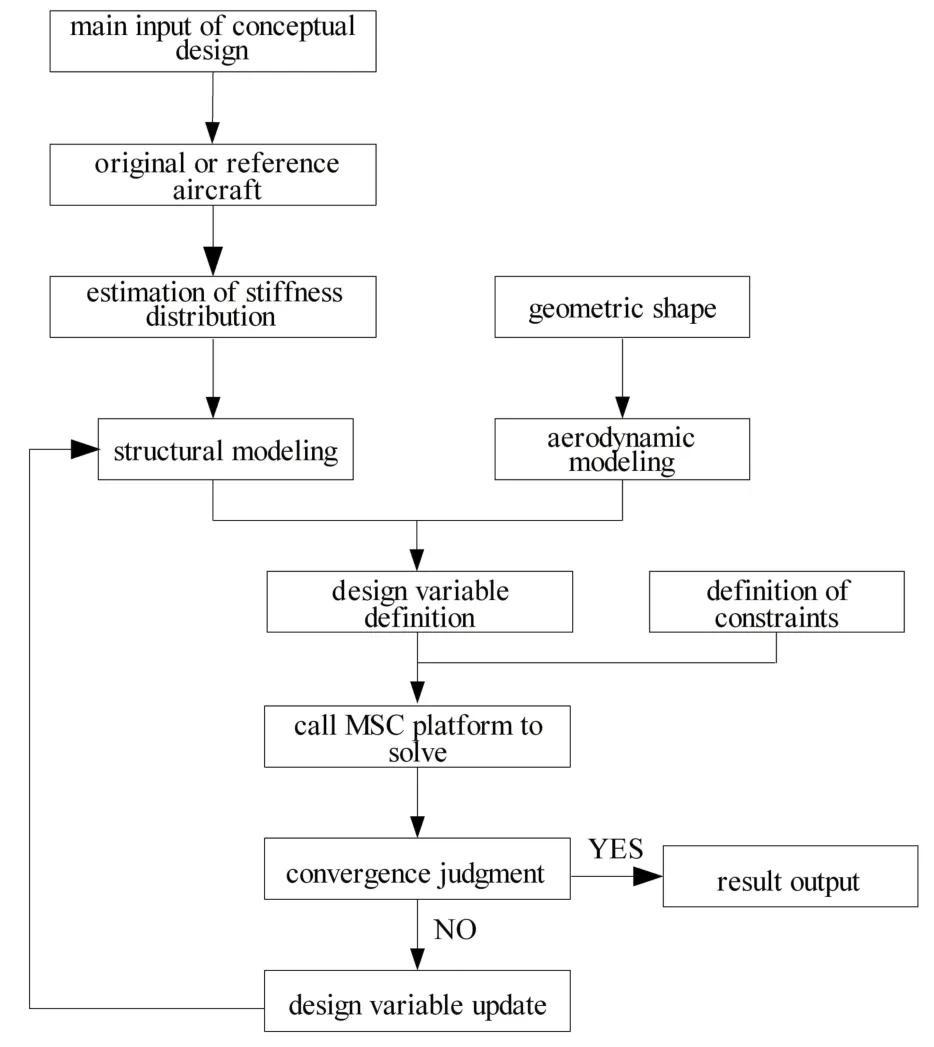
图3 气动弹性优化设计基本流程Fig.3 Flow of aeroelastic optimization design

3 优化结果

利用机翼的气动弹性模型，取典型状态马赫数Ma=0.61，飞行高度H=0 km，进行气动弹性优化求解，得到的结果分别如下.

气动弹性优化设计的目标是使机翼结构重量最小化.因此，根据结构模型的参数变化，检查了机翼结构重量的迭代过程，如图4所示.可见，为了满足优化目标，机翼结构重量开始在一定范围内出现波动，随后逐渐收敛至稳定状态，满足结构轻量化要求.图5给出了达到优化设计目标时，机翼典型部位设计变量的迭代过程.可见，在机翼结构重量收敛至最小化的前提下，为了满足颤振、根部应力、翼尖变形和发散响应等约束条件，相对初始的刚度分布而言，内翼面结构刚度应稍微增大，外翼面结构刚度则应适当减小.

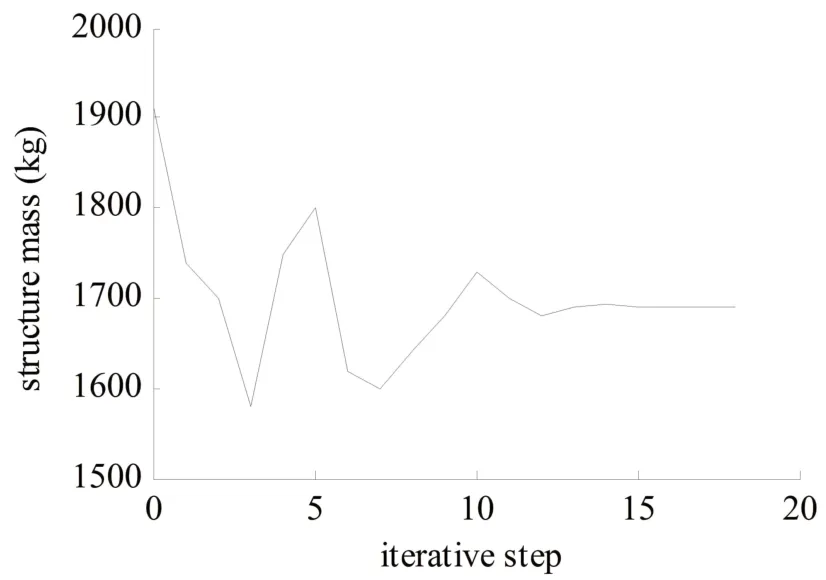
图4 机翼结构质量的收敛过程Fig.4 Convergent course of wing structure mass

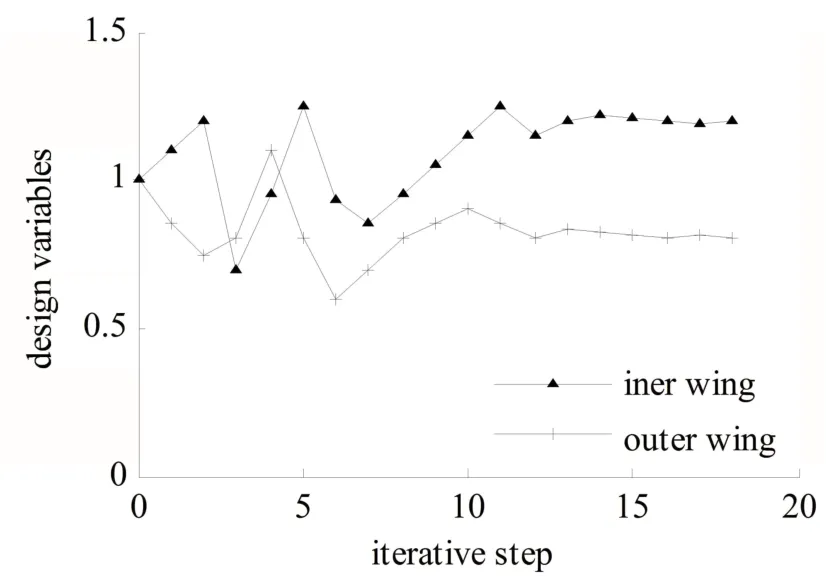
图5 设计变量的收敛过程Fig.5 Convergent course of design variables

图6、图7分别给出了利用p-k法求解得到的v-g、v-f曲线.可见，利用按照同类飞机初步确定的机翼刚度数据，得到机翼的颤振速度仅为228.39 m/s，难以满足颤振速度vf≥1.15vmax（vmax=207.58 m/s）的要求［12］.因此，在概念设计阶段，仅仅参照原型机或利用工程经验方法进行新机的刚度预估是不够的，会带来不满足气动弹性设计要求的风险，必须按照规定的气动弹性稳定性要求，对新机的刚度分布预估结果进行修正.

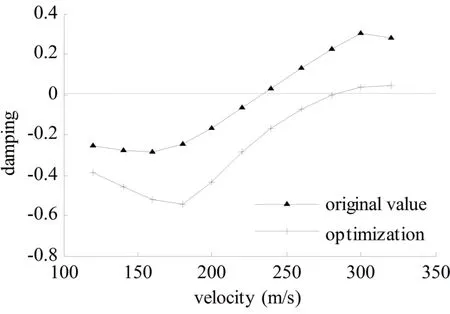
图6 v-g曲线Fig.6 v-g plot

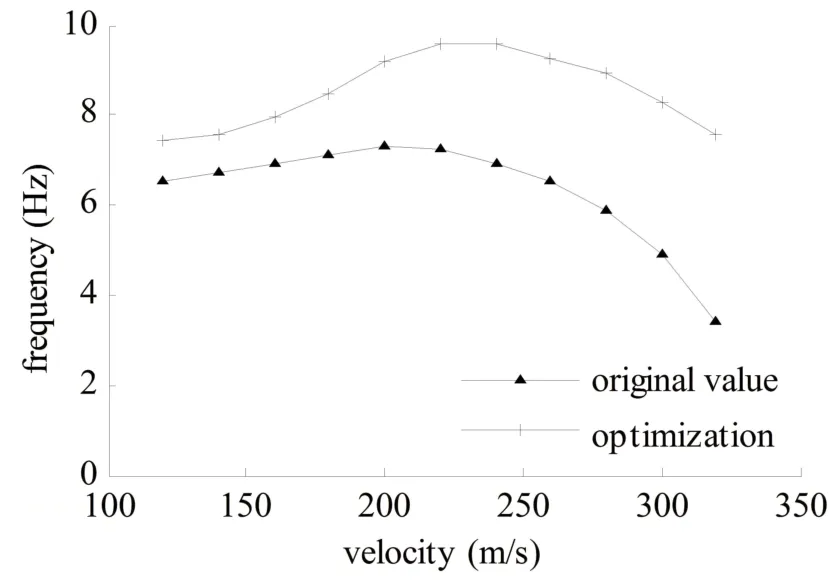
图7 v-f曲线Fig.7 v-f plot

对比分析结果可知，对机翼的刚度分布进行气动弹性优化设计后，机翼的颤振速度提高至278.65 m/s，相对优化前增大了约22%，满足颤振稳定性要求.此外，机翼的扭转发散速度也达到了327.03 m/s，满足静气动弹性设计要求，翼尖扭角、翼根应力也都满足给定的约束条件.最后，根据优化求解结果，可以得到机翼的弯曲刚度、扭转刚度沿翼展方向的分布，进而作为结构布局设计的依据，如图8所示.

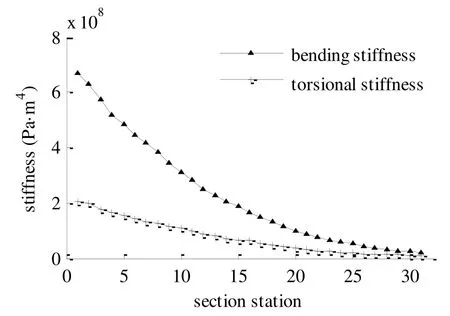
图8 机翼的刚度分布计算结果Fig.8 Stiffness distribution of along the wing span

当然，上述过程仅仅选取某一典型状态进行了机翼的气动弹性优化设计.实际上，规范要求在飞行包线内的所有状态下，飞机的气动弹性特性都应满足稳定性要求.因此，要综合考虑各种相关的设计特征，充分开展飞机气动弹性优化计算，从而尽可能地为后续的结构设计提供更有效的数据.

4 结论

飞机的气动弹性性能如发散、颤振等，对飞行品质、性能及安全有很大影响.为了在飞机概念设计阶段就计入气动弹性效应，防止气动弹性问题带来后续的设计更改甚至重新设计，就需要尽早开展考虑气动弹性约束的设计计算，指导结构设计.

本文以某典型的大展弦比机翼为例，按照给定的总体外形进行气动建模，然后参照同类飞机初步确定结构刚度分布，以结构重量最小化并满足颤振速度、发散速度、翼尖变形、翼根应力的要求为设计目标，利用优化迭代方法对机翼的展向刚度分布进行气动弹性优化求解.

结果表明，初步预估的结构刚度分布难以满足气动弹性稳定性要求，优化后的结构刚度分布同时满足强度、刚度、静气动弹性、动气动弹性及重量最小化多方面的要求.此外，根据气动弹性优化结果可以得到机翼弯曲刚度、扭转刚度的分布指标，作为后续结构设计的参考依据.