一种用于转子裂纹故障检测的区间控制策略*

任双兴 侯磊李凌峰 靳宇宏 昌泽元 姚迟森

（哈尔滨工业大学航天学院，哈尔滨 150001）

引言

随着社会和科技的发展，航空领域的研究越来越受到世界各国重视.作为提供飞行器飞行动力的核心，航空发动机结构复杂，易受激振和温度等因素影响，一直以来都是航空领域的热门课题.裂纹是发动机转子的重要故障形式，裂纹的研究在发动机的生产设计、产品检测与维护方面有着重要的意义.

国内外许多学者对转子系统故障进行了研究.伍小莉等［1］进行了转子-滚动轴承耦合系统的动力学建模，以研究不平衡-不对中故障转子系统的动力学特征.朱瑞等［2］建立了热固耦合作用下燃气轮机碰摩转子的动力学模型，对燃气轮机转子碰摩故障的振动特性进行了研究，分析结果表明：考虑转子的热固耦合作用对于燃气轮机转子的碰摩故障研究具有重要意义.现有的裂纹模型主要有：裂纹的开闭及轴刚度的变化可用阶跃函数来表示的方波模型［3］；Schmied的余弦波模型［4］考虑了裂纹半开半闭的过渡过程，综合模型［5］给出了裂纹开闭状态及过渡过程与裂纹深度、转轴在裂纹开闭处的挠曲状态之间的关系，Men的非线性模型［6］考虑裂纹和轴心位移的关系，提出了一种考虑系统非线性涡动的非线性裂纹开闭模型.

区间控制策略在工程应用中是十分普遍的.胡铭菲［7］等将区间预测控制和经济模型预测控制的目标函数结合，得到满足控制要求且经济效益更好的新型控制策略；罗雄麟等［8］提出一种基于模型预测控制理论的区间控制算法；王兰豪等［9］通过设计消除前一时刻未建模动态补偿信号叠加于基于线性模型设计的反馈控制器，提出了泵池液位和给矿压力双速率区间控制算法.

国内有许多学者也对参数激励进行了研究.孙敏等［10］研究了参数激励与外激励共同作用下的四边简支薄板在内共振下的分叉行为并进行了数值模拟；杨积东等［11］给出了重力作用下的裂纹转子系统的非线性动力响应；戎海武［12］等考虑了单自由度单边碰撞系统在有界随机噪声参数激励下的稳定性问题，发现在一定参数区域内，随机噪声使得系统稳定化；祝长生等［13］指出了常数激励可以用来简化在飞行器做恒定角速度转动时的机动载荷.由此可见，可以以转子系统在常数激励下的响应特征作为裂纹故障的检测依据.

本文以某型航空发动机为例，取其转子系统低压压气机部分建立简化的动力学模型，基于外加常数激励能够使得裂纹转子系统的超谐波响应特征显著放大的原理，构建一种能够用于转子系统裂纹故障检测的区间控制策略，通过控制算法实现在裂纹转子系统超谐共振转速区域内施加常数激励，放大超谐共振响应幅值，而在该转速区域以外不施加激励，避免对系统主共振产生影响.

1 转子裂纹系统模型

双转子结构是现代航空发动机采用的主要结构形式，这种结构的高压转子和低压转子通过中介轴承联接在一起.以某型航空发动机为例［12］，双转子系统采用的是六点支承结构，其中高压转子系统是二支点结构，采用1-0-1的支承方式；低压转子系统是四支点结构，采用1-2-1的支承方式.路振勇等［14］建立的复杂动力学离散模型结构如图1所示.该模型建立了8级高压压气机轮盘，4级低压压气机轮盘以及各1级的高低压涡轮轮盘.路振勇［15］的研究表明双转子系统的低压压气机部分相对独立，可以看作单转子系统.因此选取图1红框中的低压部分建立单转子系统模型如图2.

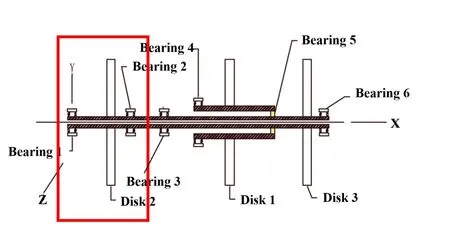
图1 航空发动机双转子动力学简化模型Fig.1 Simplified dynamical model of dual-rotor of aero-engine

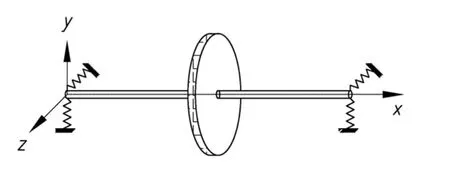
图2 单转子裂纹系统示意图Fig.2 Single rotor crack system

参考文献［16］，在图2所示的转子系统模型中，考虑盘根处出现一裂纹，并考虑在y方向上施加常数激励，建立转子系统动力学模型.

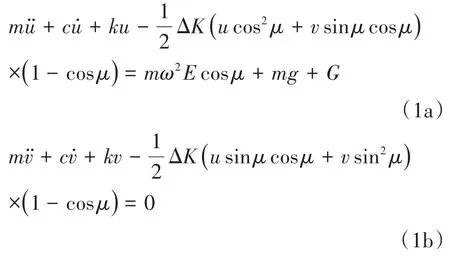
其中，m为转盘质量，c为阻尼，且c=2ζmω，ω为转速，ζ为阻尼比，ΔK为裂纹刚度，表征裂纹深度对转轴刚度的影响，k为转子系统的支承刚度，E为转盘偏心处到转盘质心的距离，g为重力加速度，G为施加的常数激励.对方程进行无量纲化：

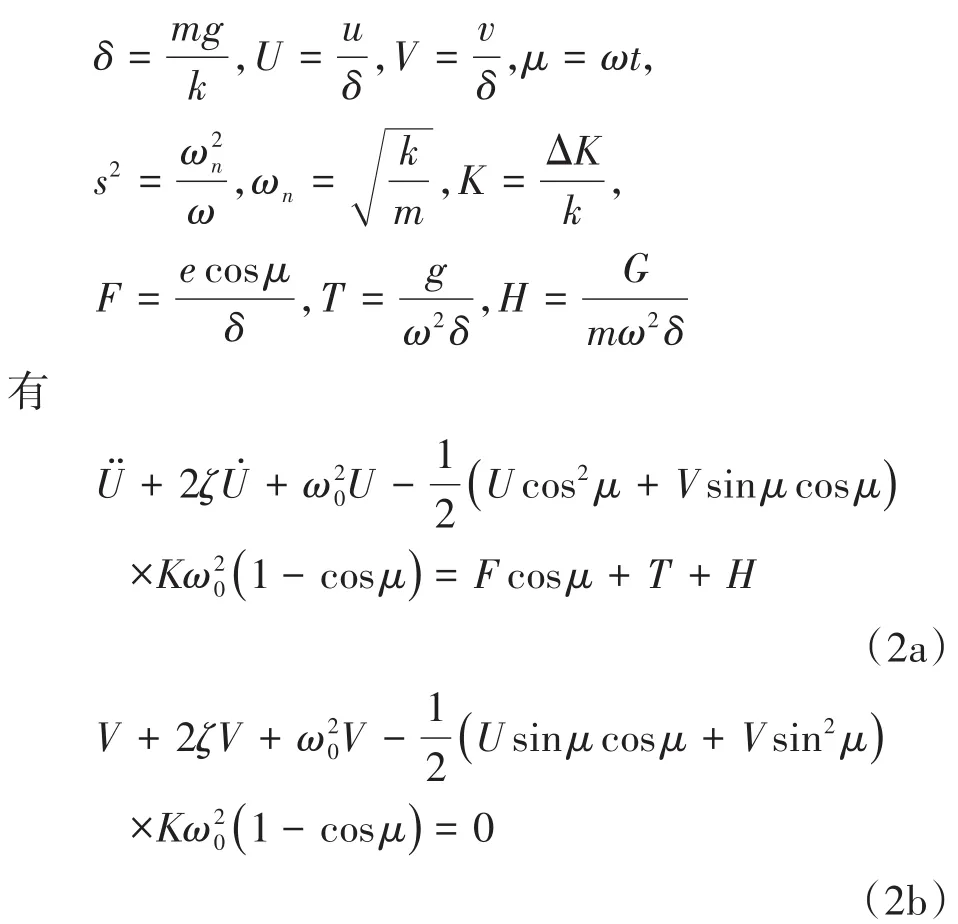
其中，ωn为系统固有频率，F为不平衡激励力，T表示重力的影响，H为外加常数激励的影响，其数值大小代表外加常数激励相对重力的倍数.

在本文的模型中，常数激励可通过电磁力施加.石北啸等［17］详细比较了电磁场和重力场在场的形状、场强、场能、量纲各方面的相似性，提出了电磁场和重力场的相似理论并实现了电磁场实际模型的建立，验证了电磁场模拟重力场的可行性.因此可以在转子系统上建设电磁场环境，利用电磁力创造模拟超重环境，使得转子系统上出现常数激励，产生“重力”成倍增加的效果.

用谐波平衡法对方程1求解，设方程（2）的解为：

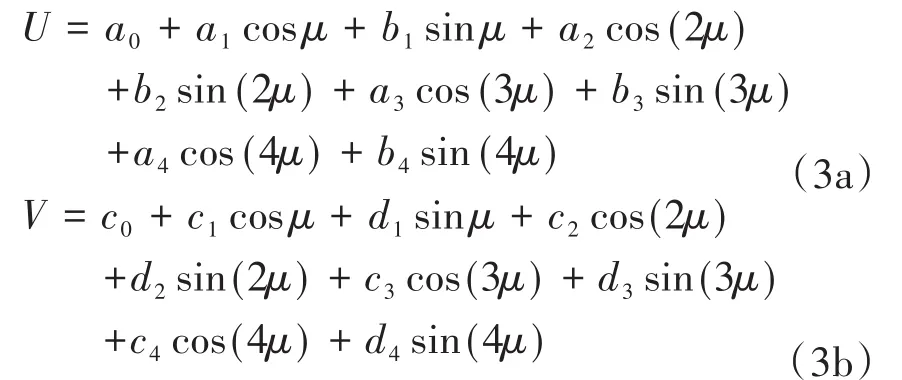
把（3）式带入方程（2），令各次谐波的系数之和为零，可以得到18个关于ai、bi、ci、di（其中i=0，1，…，4）的代数方程，解该方程即可得到18个待定系数，写成矩阵形式如下：

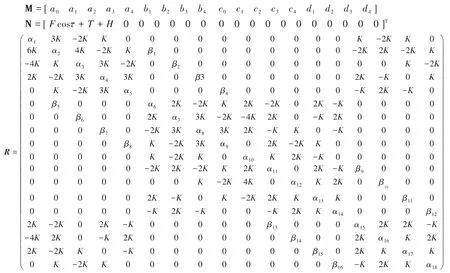
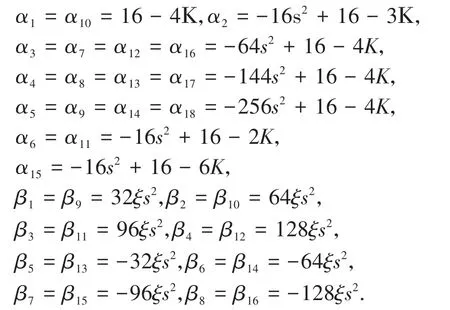
根据振动响应方程4的结果可以知道：常数激励对转子系统的主共振峰、超谐共振峰的幅值影响很大，其中超谐共振共振峰的响应幅值与常数激励正相关，而常数激励的作用方向对系统主共振峰的响应影响较大，但对超谐共振峰的响应影响很小.这表明常数激励可以成为航空发动机转子系统裂纹故障检测的一种手段.

2 区间控制策略

在工业过程控制中，由于被控变量通常具有多个中间状态变量的特点，或过程常是多变量耦合，所以各个区间采用相应的控制方法，即区间控制策略.为了使目标区间的响应更加明显以提高裂纹故障检测成功率，将区间控制策略应用在转子系统裂纹模型中.在常数激励作用下，于目标区间施加系数，以增强或者减弱振动响应.

在施加控制之前，需要先算出航空发动机转子系统临界转速的粗略值.计算临界转速的方法已经比较成熟，一些经典的计算方法有矩阵迭代法、逐段推算法、能量法等，许多学者在双转子系统临界转速的计算上也做了大量的工作，提出了多种基于传递矩阵法的改进算法，如子结构传递矩阵法、传递矩阵－阻抗耦合法、分振型－模态综合法等［18］.已知常数激励作用下的转子系统会在临界转速的1/3，1/2，1倍处产生较大的振幅响应［9］，所以可取目标区间基准值如下：以ω/3、ω/2为目标区间中位数，偏差为±ω/20，即［17ω/60，23ω/60］，［9ω/20，11ω/20］作为转速的目标控制区间，并对它们施加系数控制.

对区间控制策略下的方程2进行动力学仿真，建立仿真系统如图3所示.在无控制的自然状态下求出临界转速ωz，然后将转速区间按（ωmin，ωz-11），（ωz-10，ωz+10），（ωz+11，ωmax）分成三部分，分别施加五倍重力、二十倍重力、五倍重力.将每个区间所得的同一方向上的矩阵结果串联，将转子系统有关参数作为系统的输入信号，将转子系统的振动响应作为系统的输出信号，绘制幅频响应曲线.

图3 转子系统仿真框图Fig.3 Diagram of rotor system simulation

3 仿真结果与分析

3.1 理想情况下仿真效果

在实际的转子裂纹检测过程中，转子系统所处的环境往往存在着热噪声等多种噪声信号，它们对转子幅频响应曲线的影响不能简单地忽略不计，因此必须在模型中加入噪声的扰动影响.噪声选用高斯白噪声，其方差设置为1，均值设置为0，并选择移动平均滤波器对响应曲线进行滤波处理.无控制的自然状态下无噪音和噪音环境下单转子系统的裂纹响应特征如图4和图5所示.

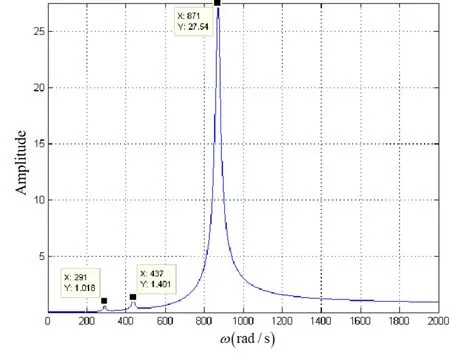
图4 无控制状态下裂纹转子系统幅频响应曲线Fig.4 Amplitude-frequency response curve of the cracked rotor system under uncontrolled state

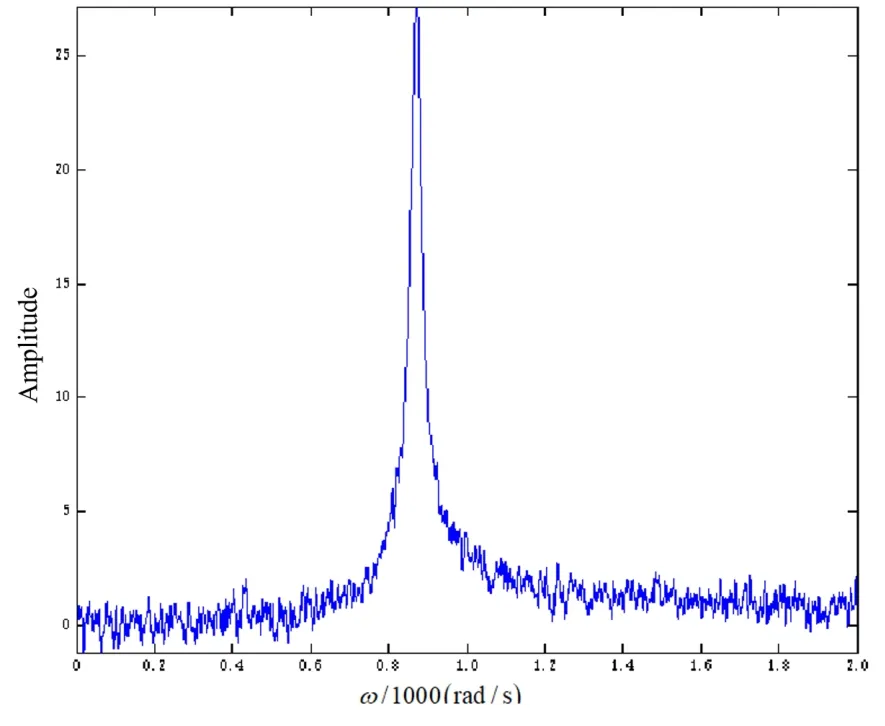
图5 无控制状态下噪音幅频响应曲线Fig.5 Amplitude-frequency response curve in noisy environment under uncontrolled state

从图4可以看出，在没有噪声信号影响的一倍重力作用下，转子系统也会存在超谐响应.这是因为转子重力也可以视为一种常数激励，但是激励比较小，所以超谐响应峰要比主共振峰小得多，尤其是四分之一临界转速处的超谐响应几乎观测不到.从图5中可以看出，加入噪声影响后，在无控制的自然状态下的幅频响应曲线中已经看不到明显的超谐响应，这是因为超谐响应的信号与噪声信号一起被滤波器过滤掉了.

3.2 区间控制仿真结果

在模型中加入区间控制策略后得到的单转子系统的幅频响应特征如图6和图7所示.由图6可知，在目标区间施加5倍重力常数激励后，超谐响应共振峰的信号得到显著放大，其中四分之一临界转速处的超谐响应可以明显被观测到，而三分之一临界转速处和二分之一的超谐响应信号与无控制的自然状态相比也放大了接近4.6倍，基本与主共振峰达到了同一个数量级.由此可见，相比单一常数激励，区间控制策略下的常数激励对转子裂纹区域的超谐响应特征信号具有明显的放大作用.理论上来说，增大常数激励，可以得到更高的超谐共振峰值，也更有助于实现裂纹故障诊断，这在文献［16］中已有相应报道.

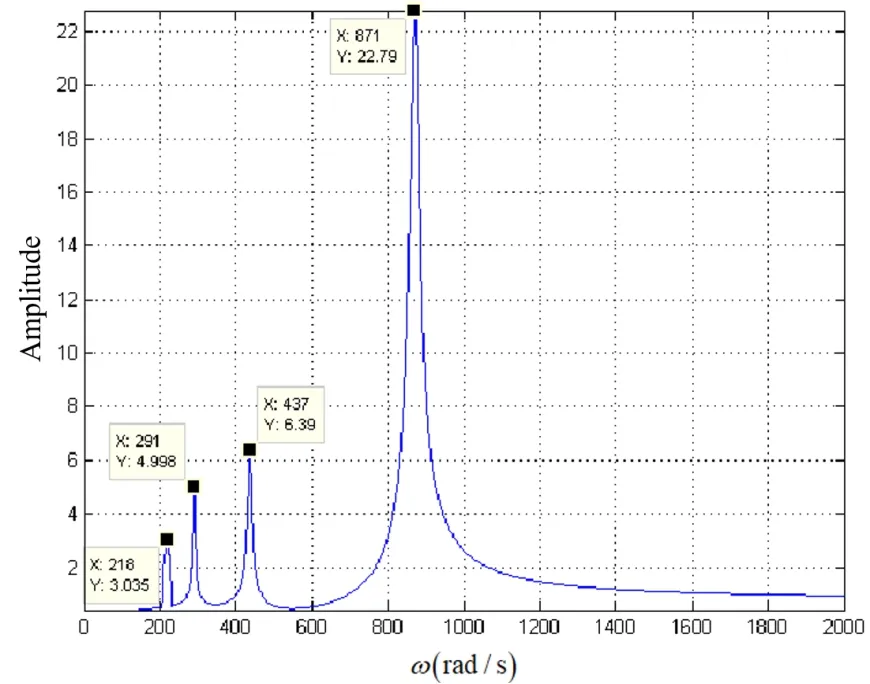
图6 无噪音环境下区间控制策略幅频响应曲线Fig.6 Amplitude-frequency response curve with switching control strategy

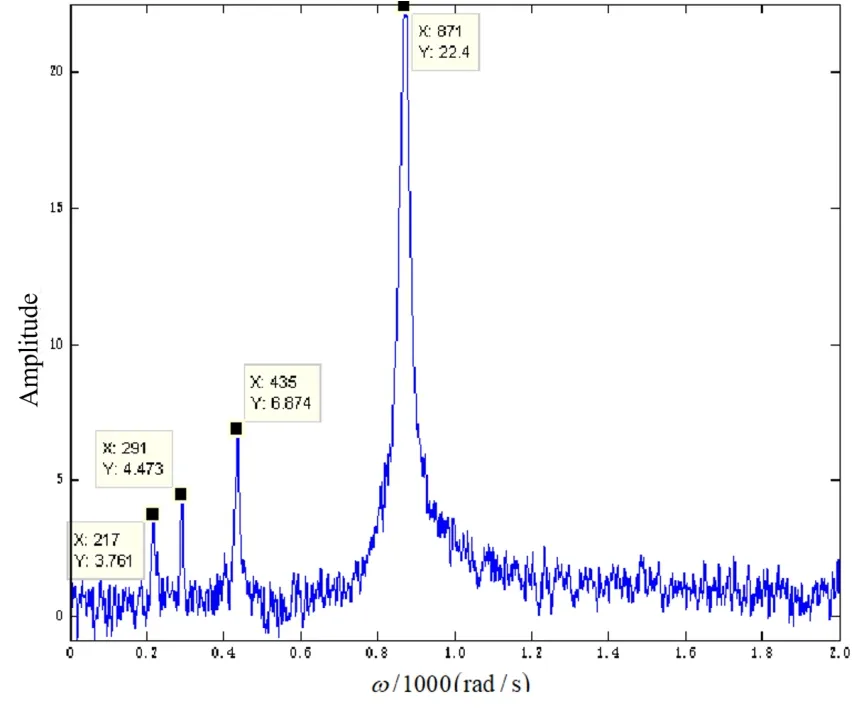
图7 噪音环境下区间控制策略幅频响应曲线Fig.7 Amplitude-frequency response curve of switching control strategy in noisy environment

由图7可以看出，噪音环境中，区间控制策略作用下的转子系统的幅频响应曲线中仍然可以明显地观测到超谐响应的共振峰，这说明区间控制策略下的常数激励模型在噪声影响下对裂纹区域的响应依然具有良好的放大作用.因此，若能将区间控制策略应用在实际裂纹的早期检测中，裂纹区域的响应将会更加突出，以便及时维修或更换部件，能够有效降低事故发生率.

在已进行的噪音环境下两种控制状态的转子系统的幅频响应特性研究的基础上，进一步开展不同信噪比参数下区间控制策略有效性的研究，结果如图8和图9所示.从图中可以看出，在无区间控制状态下，信噪比在16dB时就已经无法识别二分之一超谐响应的共振峰；而在区间控制策略作用下的幅频响应曲线中，信噪比，在6dB时依然可以识别出三分之一的超谐响应的共振峰，在3dB时依然可以识别出二分之一的超谐响应的共振峰.由此可见，通过应用区间控制策略，有效检测的信噪比可以达到3dB.

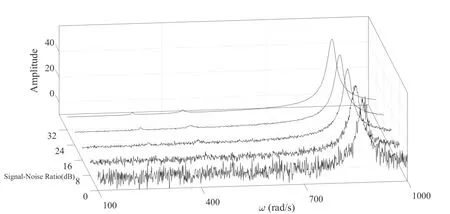
图8 无控制状态下不同信噪比的幅频响应曲线Fig.8 Amplitude-frequency response curves with different signal-to-noise ratios under uncontrolled conditions

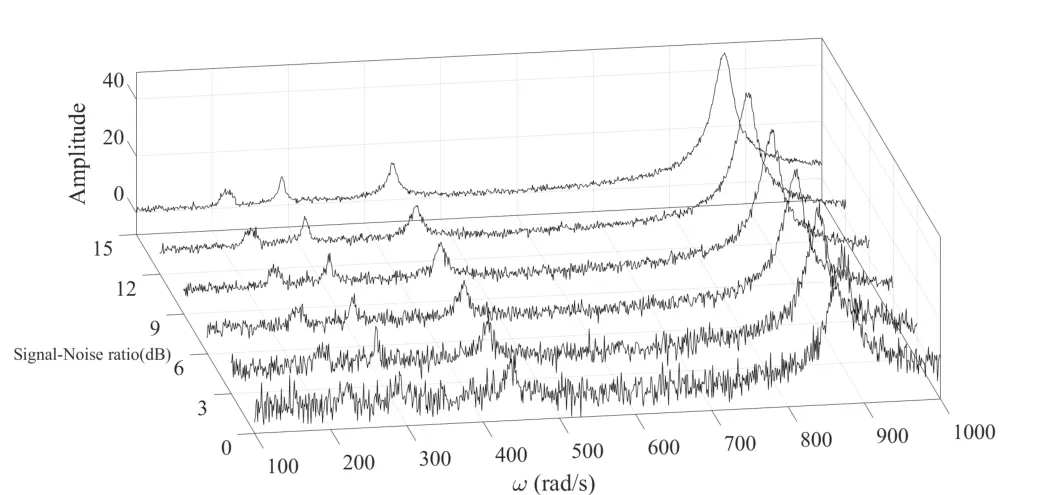
图9 区间控制策略不同信噪比的幅频响应曲线Fig.9 Amplitude-frequency response curves of switching control strategy with different signal-to-noise ratios

4 结论

本文提出一种用于转子裂纹故障检测的区间控制策略，以某型航空发动机转子系统低压压气机部分为研究对象，建立裂纹转子简化动力学模型，并考虑外加常数激励的作用，应用Matlab软件构建了Simulink仿真程序，并考虑噪音环境，研究了基于区间控制策略实现裂纹检测的仿真效果.结论如下：

（1）超谐波共振是转子系统裂纹故障的振动响应特征，但在噪音状态下，该特征信号往往很微弱，难以检测到；

（2）常数激励能够对裂纹转子系统的超谐波共振响应产生显著的放大作用，利用该原理构建了一种区间控制策略，能够提高转子系统裂纹故障检测的成功率；

（3）通过Simulink仿真表明，在五倍重力常数激励下，应用区间控制策略，使得超谐响应共振峰的幅值增大4.6倍，能够实现噪音环境下转子系统裂纹故障的有效检测；

（4）通过开展不同信噪比参数下区间控制策略的有效性研究，发现在无控制状态的转子系统在信噪比16dB时就无法识别出超谐响应共振峰，而应用区间控制策略后，故障有效识别的信噪比可以达到3dB.

后续研究将考虑通过电磁轴承作为激振器给转子系统施加常数激励，通过试验测试来进一步验证本文的结论.