忆阻器的温度效应改进模型及其仿生神经突触传递*

张蒙 成宇 张艺 朱庆花 韩芳†

（1.东华大学信息科学与技术学院，上海 201620）（2.东华大学材料科学与工程学院，上海 201620）

引言

大量研究表明，温度对脑功能有着显著影响.从医学角度来看，强烈建议严格控制患者在创伤修复时期的体温［1］.然而，尽管已经开发了控制脑部温度的技术，但温度影响神经电活动的直接机制仍不清楚［2］.了解温度对脑功能的影响有助于开发更有效的方法来治疗对温度敏感的各种神经系统疾病，包括热水癫痫病、自闭症和脑损伤等［3］.此外，某些神经生物学实验（例如体外研究）通常在低于生理学的温度下进行.因此，探究神经突触传递的温度依赖性对体外和体内研究的共融至关重要.

在单个神经元水平上，已经发现温度对脑功能的多种影响，主要包括细胞膜静息电位、离子通道的动态特性、突触传递［3］三个方面，其中前两个方面已经通过建模得到了较好的体现.但事实证明温度对突触传递的影响更难建模，这主要是由于突触传递涉及多种动态过程，如神经递质的释放、囊泡孔的动力学特性、神经递质的扩散、神经递质的结合和突触后受体的动力学特性等.温度对每个过程的影响是不同的，它们共同决定突触传递的效能.

忆阻器作为第四种基本电路元件，由美国加州大学的蔡少棠教授于1971年提出［4］，2008年惠普实验室首次研制出实物忆阻器［5］.忆阻器具有类似生物突触的非线性传输特性，且其捏滞回线的非线性特征易于产生混沌、分岔等复杂动力学行为，基于其构建的多种突触电路、Hodgkin-Huxley和FitzHugh-Nagumo神经元电路以及简单神经网络电路的混沌与同步等行为已经得到了广泛研究［6-10］.并且由于忆阻器的纳米级尺寸，将极大地减小神经电路的规模与能耗.同时，忆阻器的行为特性也受到多种因素的影响，其中设备内部温度是重要因素之一，强烈影响忆阻器内部离子和空位的迁移与扩散，在建模时必须谨慎分析［11］.Graves实测分析了氧化钽忆阻器随温度变化的电导性质，发现电导在室温以上对温度有强烈的依赖性，而对低于室温的温度不敏感［12］.Kocyigit研究了温度对氧化锌忆阻器电导率的影响，发现两者随温度升高而增加［13］.Kim研究了温度对HfOx/AlOy忆阻器的电导和长时程可塑性的影响［14］.以上忆阻器均缺乏相应的数学模型，在神经系统建模过程中无法直接应用.Singh通过建立温度依赖的氧化钛忆阻器电导模型，得到温度相关的迁移率表达式，进而实现忆阻开关参数的温度依赖性建模［15］.Pahinkar对氧化铪忆阻器建模时考虑了偏压作用下温度对氧空位迁移率的促进作用，但未包括无外界电场作用下的回扩散过程［16］.这些模型均属于离子迁移模型，可以模拟生物突触的非线性传输特性，但在突触可塑性模拟方面仍有不足，即无法解释短期可塑性（shortterm plasticity，STP）、长 期 可 塑 性（long-term plasticity，LTP）和记忆衰退等现象［17］.Meng和Wang所提出的忆阻器模型仅考虑了温度对离子扩散的影响，忽略了其对离子迁移的作用［17，18］.Du 提出的二阶氧化钨忆阻器模型，建模时同时考虑了离子迁移和扩散过程，虽然此模型在突触可塑性模拟方面优势明显，包括放电时间依赖可塑性、双脉冲易化、STP、LTP以及相互转换［19-21］，但未考虑温度对迁移和扩散的影响.

本文将基于文献［19］提出的忆阻器数学模型改进忆阻突触权值的保留项，并考虑温影响，从而引入温度变量，从理论上完善原模型的不足.为了体现温度对突触传递的影响，首先，在一定范围内控制温度变量，研究忆阻突触电导率的变化；其次，将该忆阻器作为突触连接两个相同的HH神经元，研究温度对兴奋性突触后膜电位的影响，并将仿真结果与神经生理实验进行对比.

1 氧化钨忆阻器模型

1.1 原模型

忆阻器的一个重要应用是作为神经突触应用到神经形态系统中［17］.为了模拟突触的非线性传输特性，目前已经制作出多种不同材料的忆阻器.文献［19-21］介绍了一种Pd/WOx/W结构的忆阻器，该忆阻由顶部钯电极、氧化钨开关层和底部钨电极三部分组成，其基本结构和实测输入输出特性如图1（a）所示.在正/负电压作用下，相邻扫描周期的伏安特性曲线均有重叠，这是由于在扫描间隔期间，偏压作用下氧空穴的定向迁移作用小于因浓度差而引起的扩散作用造成的，这有别于传统的离子迁移模型.为了对该忆阻器进行数学建模，文献［19］考虑到在偏压作用下，金属-半导体-金属结构可能产生肖特基势垒和隧道效应，该元件正是通过外部电压改变二者之间的关系来进行工作的.基于此，建立了WOx忆阻器的数学模型，其特性方程如下所示：

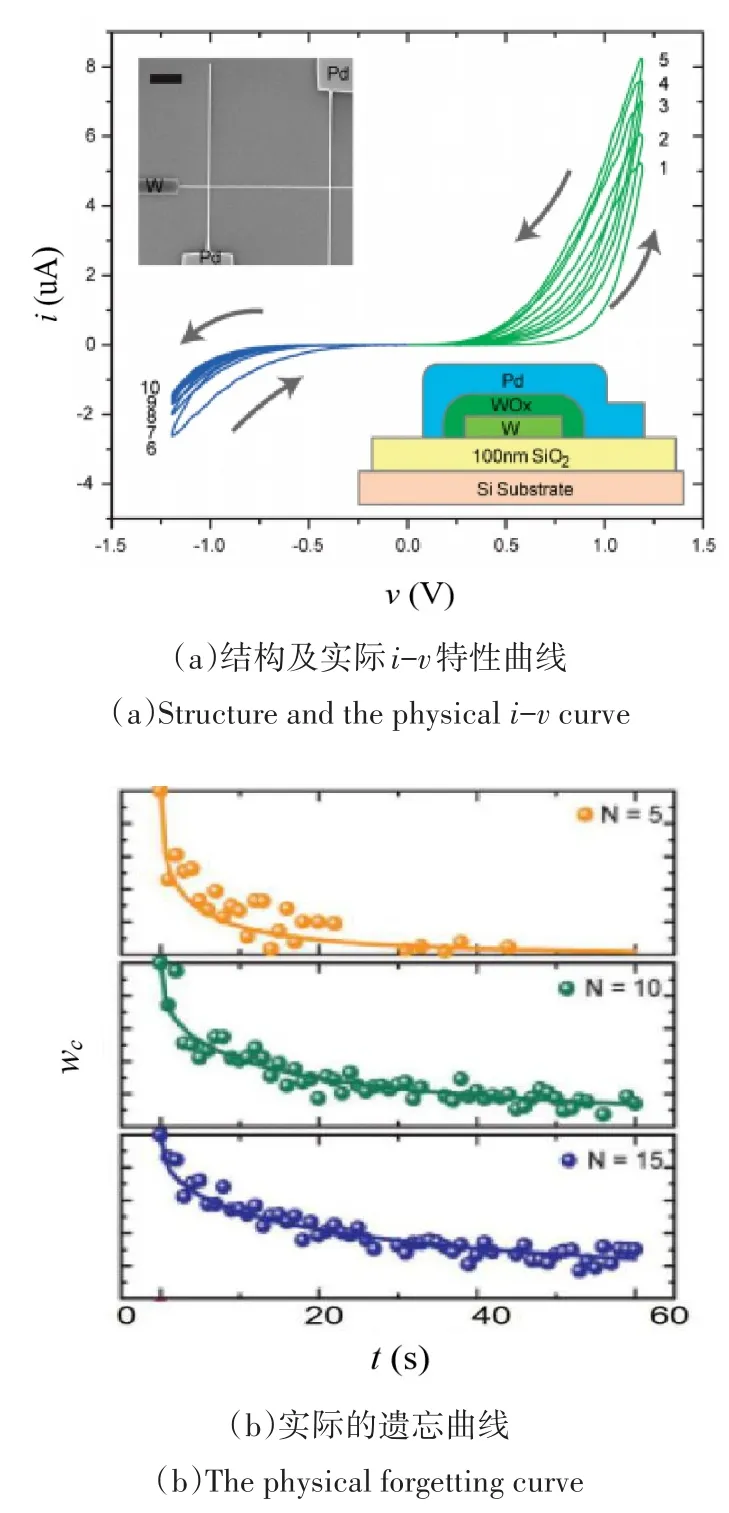
图1 氧化钨忆阻器的介绍（出自文献［19］）Fig.1The introduction about WOxmemristor（from Reference［19］）

其中，公式（1）为其伏安特性方程，v表示忆阻器的输入电压，i表示流经电流，方程右端表示存在两个并联导电通道，分别是肖特基项和隧道项，彼此间的相关权重由内部状态变量ωc所决定，其代表导电区域面积的有效面积指数，亦可认为是器件的电导率，在［0，1］区间之内变化；α，β，γ，k均是由材料特性决定的固定正参数，其物理意义依次为肖特基势垒高度、隧道势垒高度、肖特基势垒区域的耗尽层宽度、导电区域的有效隧道距离.公式（2）和公式（3）分别是两个状态变量ωm和ωc的动力学方程，其中第一项描述激励电压的影响，第二项描述具有不同有效时间的衰减效应，ωm表示氧空位的有效迁移率.公式（2）展现了在外加电压驱动下氧空位迁移占主导地位，氧空位的有效迁移率增加，当撤去外加电压时，氧空位扩散占主导地位，氧空位的有效迁移率降低.公式（3）通过exp(εωm)因子体现氧空位的移动对ωc的影响.公式（4）为氧空位的有效衰减时间函数，采用该种形式是为了更好地捕获拉伸指数类型的衰减，而不是简单的指数类型衰减，其中τs为短时程的驰豫时间常数.公式（5）为电导率的有效衰减时间函数，以便当t小时（ωm大时），电导衰减遵循短时程衰减常数（τs），而当t大时（ωm小时），电导衰减遵循长时程衰减时间常数（τl）.公式（6）为窗函数，旨在控制ωm，ωc的取值范围.根据其特性方程进行仿真，结果见文献［19］.

综合考虑，原忆阻器数学模型能较好地体现突触传递的功能.但由于原文采用了对称的正负电压扫描，致使忽略了一些重要细节，当施加不同数目的相同正脉冲时，撤去外加电压之后，忆阻器的电阻率衰减之后会维持不同的值，称之为保留值，如图1（b）所示.然而，在原模型的基础上进行仿真，当在忆阻器两端施加不同数目，幅值1V，脉冲宽度1ms的正脉冲时（图2中蓝色实线所示，N=5/10/15，N表示脉冲数目），随着外界刺激数目的增加，电导率在经过短时程（STP）衰减进入长时程（LTP）之后均会保持在电导率的初始值左右（图2中红色虚线），这与该忆阻器实际电导率变化曲线大相径庭.同时，原模型中公式（2）未考虑温度对迁移的影响，公式（4）将温度相关的短时程衰减时间τs设为常数也不符合实际，显然原模型存在明显不足.

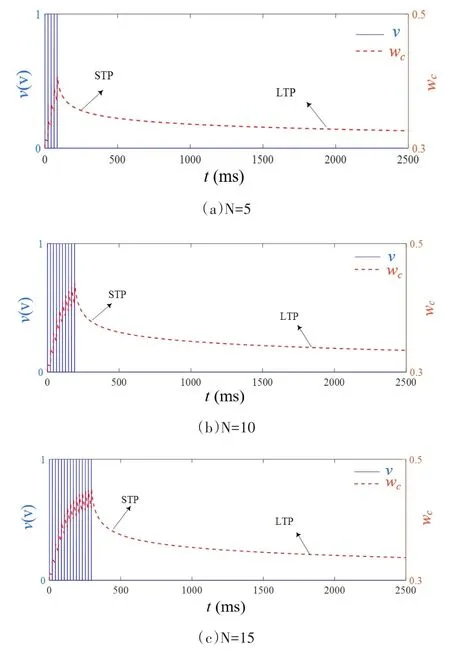
图2 原数学模型在不同数目外界刺激下的忆阻突触遗忘曲线Fig.2 Memristive synaptic forgetting curve of the original mathematical model under different numbers of external stimulus

1.2 改进的氧化钨忆阻器的温度效应模型

迁移和扩散是离子的常见运动形式，迁移是指在外界电场作用下的离子定向运动，而扩散主要是由浓度差引起的，同时温度和材料也是重要影响因素.基于上述原模型的不足，本文进行了如下两点改进.首先，将电导率的初始值和保留值分开考虑，为了简化分析，初始电导率ωc0取值为正常数，保留值ωcn主要受外加电压的作用，刺激频率越高持续时间越久，氧空位浓度越高，保留值越大［17］.其次，鉴于WOx的导电特性是温度依赖的（温度越高电导越大［22］），为了体现温度对氧空位迁移和扩散的影响，参考了描述氧空位运动速率vo［11］和扩散时间τs［18］的数学模型.其中，

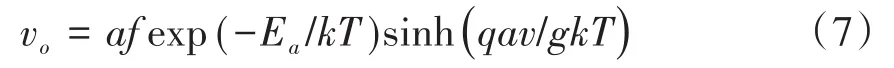
a为有效跳跃距离，f为尝试逃逸频率，Ea为空位迁移激活能，k为玻尔兹曼常数，T为温度，q代表单位电荷量，v为外加电压，g是缺氧层厚度，扩散时间为：

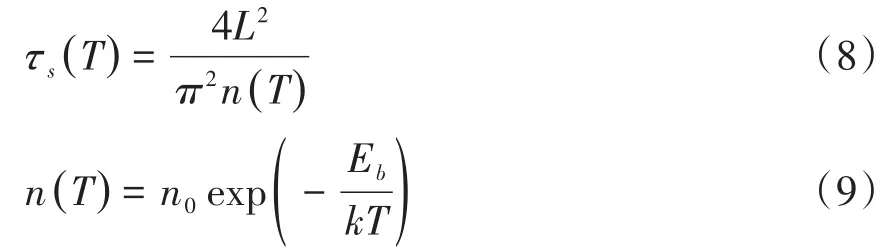
L表示初始富氧层宽度，n(T)为扩散系数，n0代表温度趋近无穷大时的扩散系数，Eb为扩散激活能.改进后的忆阻器模型部分公式如下：

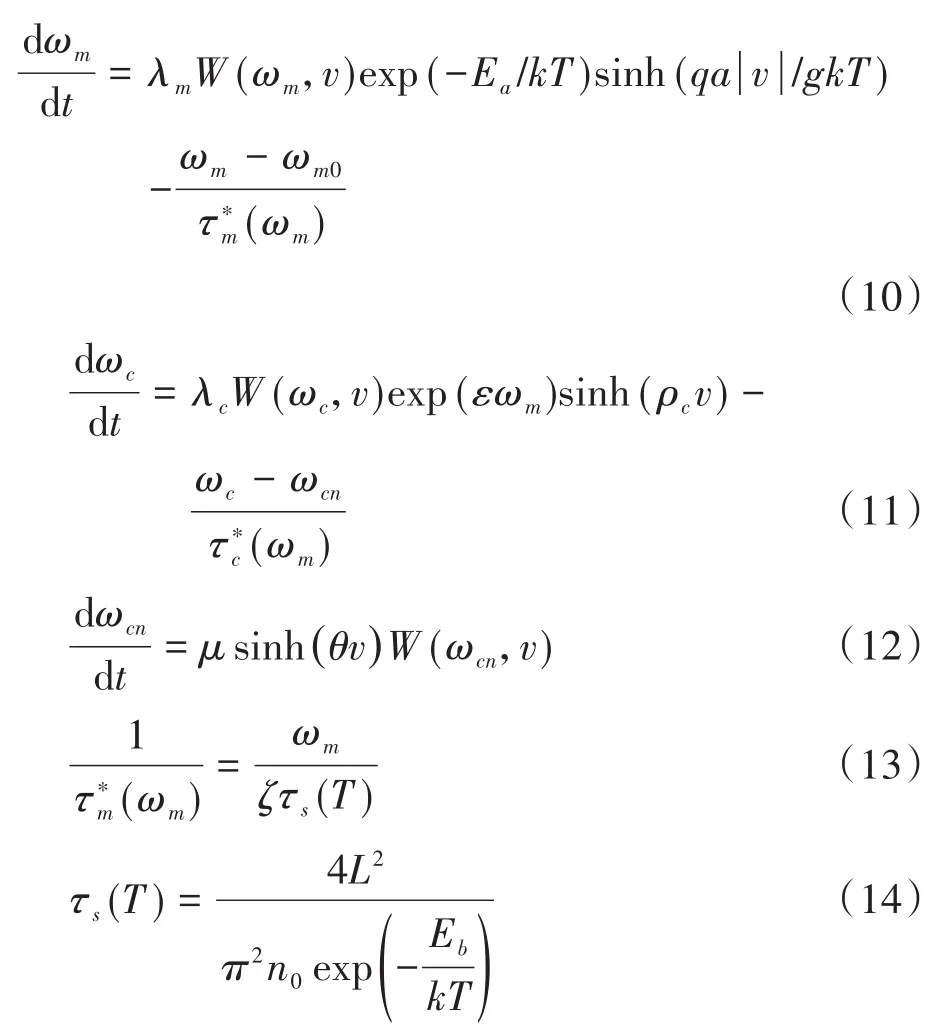
较之原模型，改进体现在如下方面：公式（10）为引入温度变量后的氧空位有效迁移率微分方程；公式（12）为电导率保留值表达式；公式（13）为温度有关的驰豫时间方程；μ，θ，ζ均为正常数.基于改进的数学模型，在如图3（a）蓝色虚线所示的三角波电压作用下，其电流随时间变化如红色实线所示，图3（b）为忆阻器的典型捏滞回线，图3（c）和图3（d）表示氧空位有效迁移率ωm和电导率ωc在不同扫描周期的变化情况，证实改进的数学模型同样可以实现原模型的功能.进一步，在不同数目的相同正脉冲作用下，其电导率和电导率保留值变化曲线如图4所示，随着刺激数目的增加，电导率保留值ωcn逐渐增加，导致在N=5/10/15时，电导率ωc衰减进入慢时程之后依次保持在0.33/0.36/0.38左右，即随着外界刺激数目的增加，忆阻保留值升高，较之原模型电导率变化情况，显然图4更加契合实测遗忘曲线.

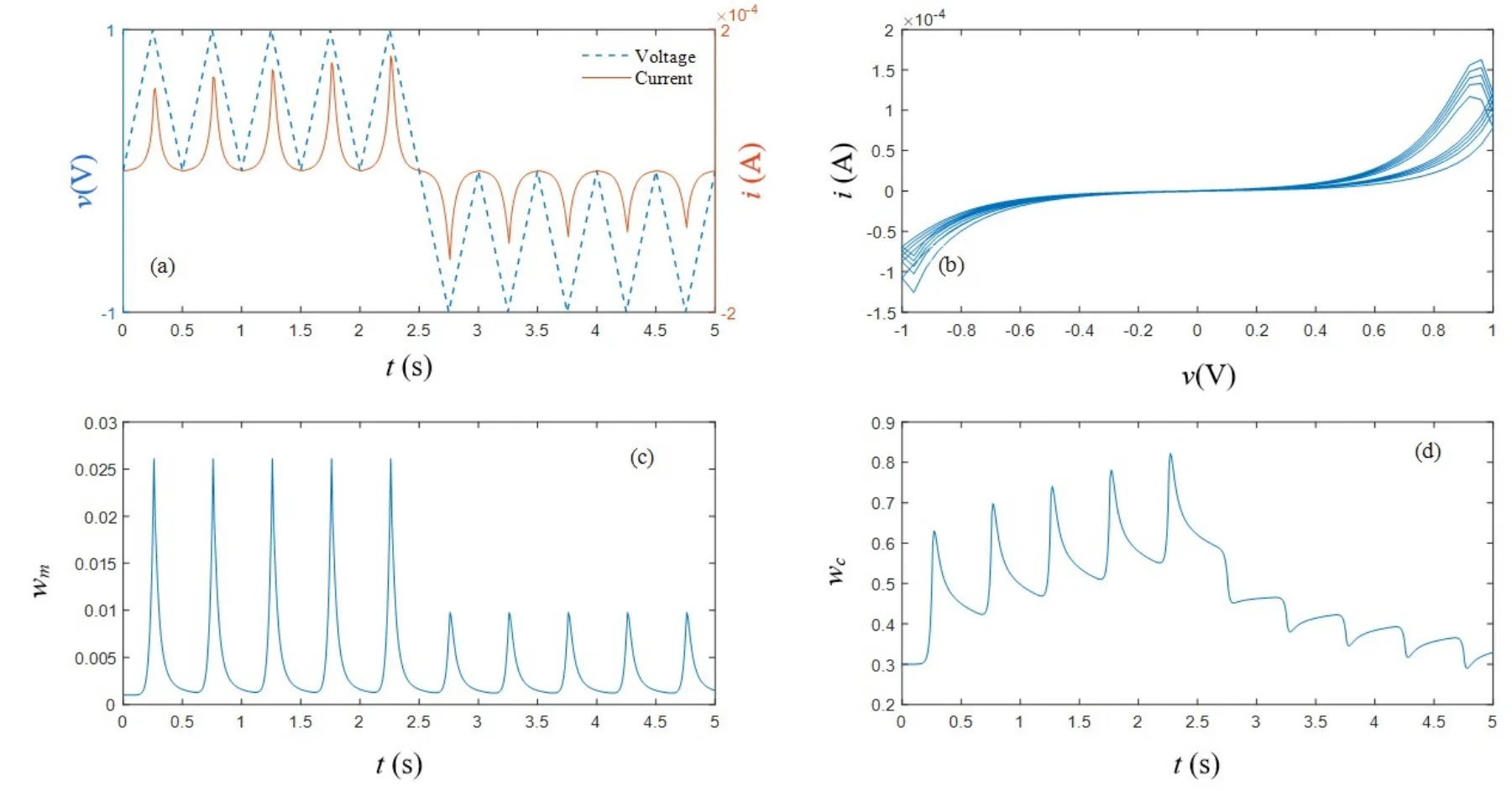
图3 改进的忆阻器数学模型在连续正（负）扫描电压下仿结果，T=300K（a）v-t，i-t曲线；（b）i-v曲线；（c）ωm-t曲线；（d）ωc-t曲线Fig.3 The simulation results of the improved WOx memristor with continuous positive（negative）input，T=300K（a）v-t，i-t curve；（b）i-v curve；（c）ωm-t curve；（d）ωc-t curve

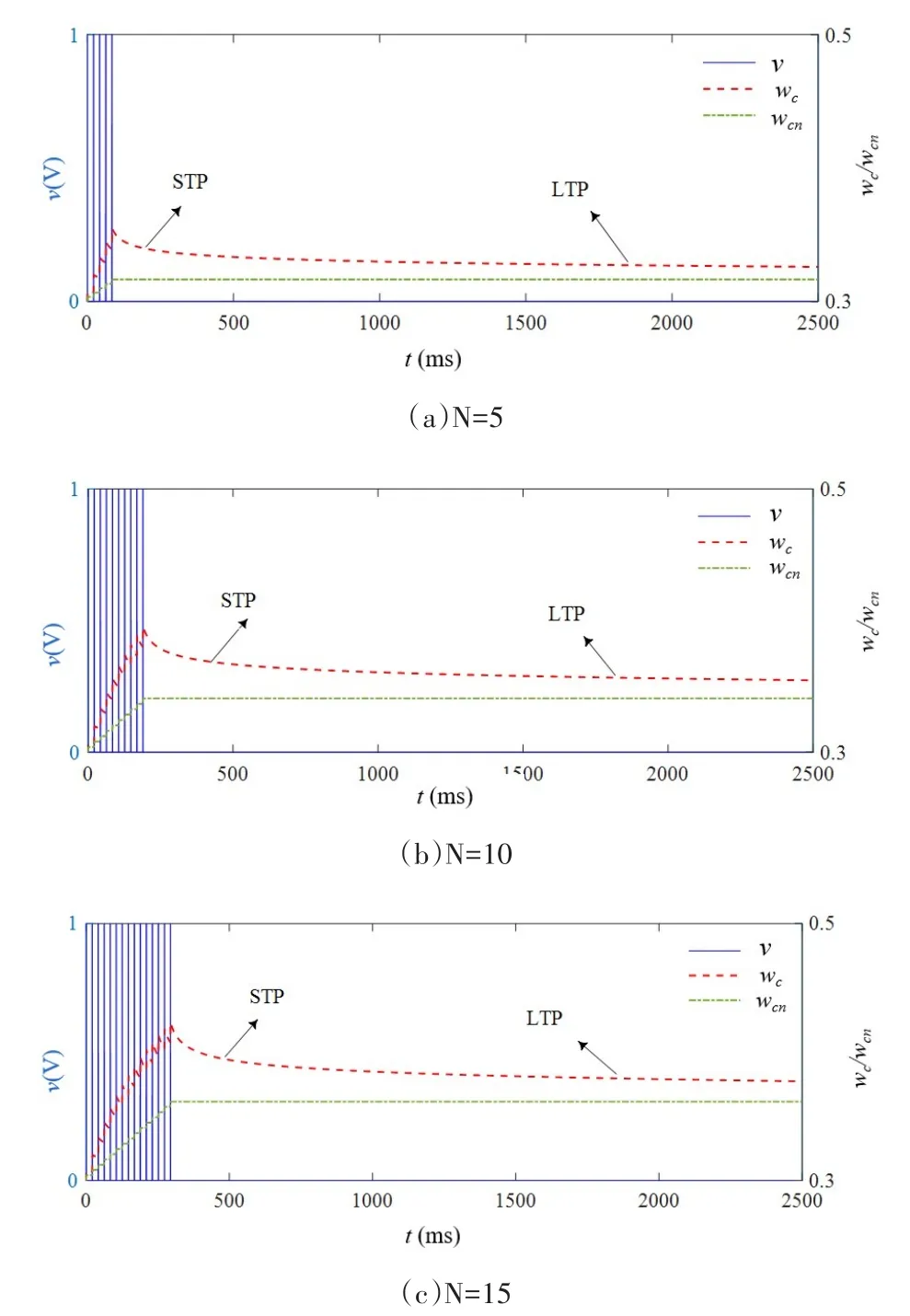
图4 改进的数学模型在不同外界刺激数目下的忆阻突触遗忘曲线，T=300KFig.4 The memristive synaptic forgetting curve of the improved math‑ematical model under different numbers of external stimulus，T=300K

2 温度对忆阻突触权值的影响

突触传递是温度敏感的，低温时突触前末端分泌的递质数量通常会减少，并且这种分泌发生所需的时间会增加.由于递质的释放主要通过突触前神经元的去极化和随后进入突触末端的钙离子量来控制，因此这些变量中的一个或两个都可能与突触传递的温度敏感性有关.通过引入的公式（7）和公式（10），可以看出温度上升引起氧空位迁移速率加快，类似于温度升高对钙离子分泌和运输的促进作用［23］，新模型更加符合突触传递的生理过程.因此本文分别采用忆阻器氧空位浓度和电导率ωc模拟生物突触中的钙离子浓度和突触权重［19］.

进一步，我们仿真了在幅值1.1V持续时间1ms的单个脉冲刺激下，不同温度下忆阻突触权值的变化曲线图，如图5所示.仿真结果显示，针对偏压作用下离子迁移过程导致的忆阻电导率变化情况，当温度处于270K至290K时，忆阻器权值变化较小，即低温不敏感；当温度在310K至330K之间递增时，忆阻电导率明显增大，即强烈的高温依赖特性，该结果与离子迁移型的氧化钽忆阻器的实测结果相一致［12］；针对温度依赖的扩散过程，温度越高扩散速率越大，弛豫时间越短，忆阻权值降低越快，该现象同样符合氧化锌忆阻器的实测结果［18］.由此可见，温度是影响此种忆阻突触权值的重要因素.

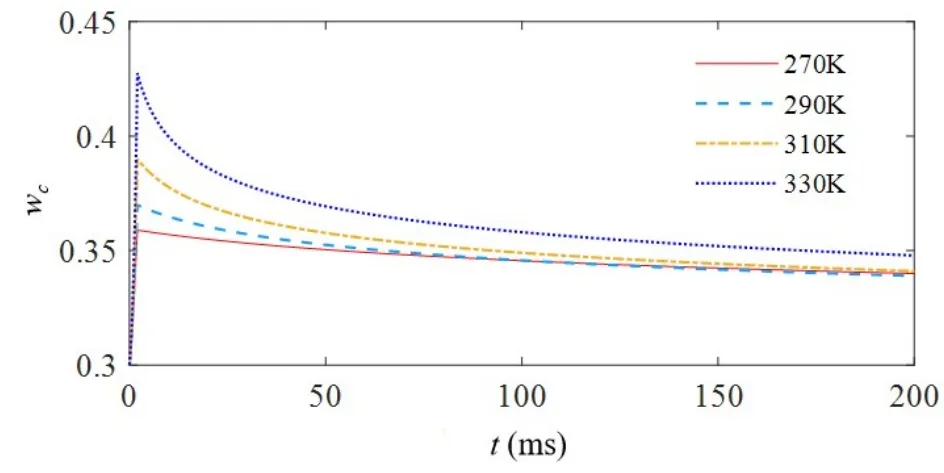
图5 不同温度下忆阻突触权值变化曲线Fig.5 The curves of memristive synapse weight change under different temperatures

3 温度对兴奋性突触后膜电位的影响

突触是神经元之间在功能上发生联系的部位，也是信息传递的关键部位，按照功能可分为兴奋性突触和抑制性突触，前者使突触后细胞的兴奋性上升，后者反之.文献［23］通过对枪乌贼的巨型突触进行生理测试，得到了不同温度下的兴奋性突触后膜电位的变化情况，发现尽管降低了突触前神经元动作电位的幅值和持续时间，但随着温度升高，突触后膜的的兴奋性动作电位仍然明显升高.众所周知，减小突触前神经元动作电位的幅值和持续时间会诱使轴突末梢释放较少的神经递质，因此兴奋性动作电位的上升必定是高温诱发的.由此可见，在某种程度上，较之突触前神经元的去极化状态，温度对突触传递的影响更大.

上文所述的氧化钨忆阻器，可以模仿生物突触的一系列可塑性，包括放电时间依赖可塑性（STDP）、双脉冲易化（PPF）、STP、LTP以及相互转换等.基于其电导变化率ωc在［0，1］之间，单个忆阻器只能模仿兴奋性突触的功能.本文采用单个忆阻器对两个Hodkin-Huxley神经元模型［24］进行单向耦和，电路原理图如图6所示.其中，对突触前神经元直接施加外部刺激电流致使其发生峰/簇放电行为，而突触后神经元所接收的刺激来自于忆阻突触电流和外部刺激电流，数学模型描述如下：

图6 基于忆阻器耦合的双HH神经元电路原理图Fig.6 Schematic diagram of dual HH neurons circuit based on memristor coupling

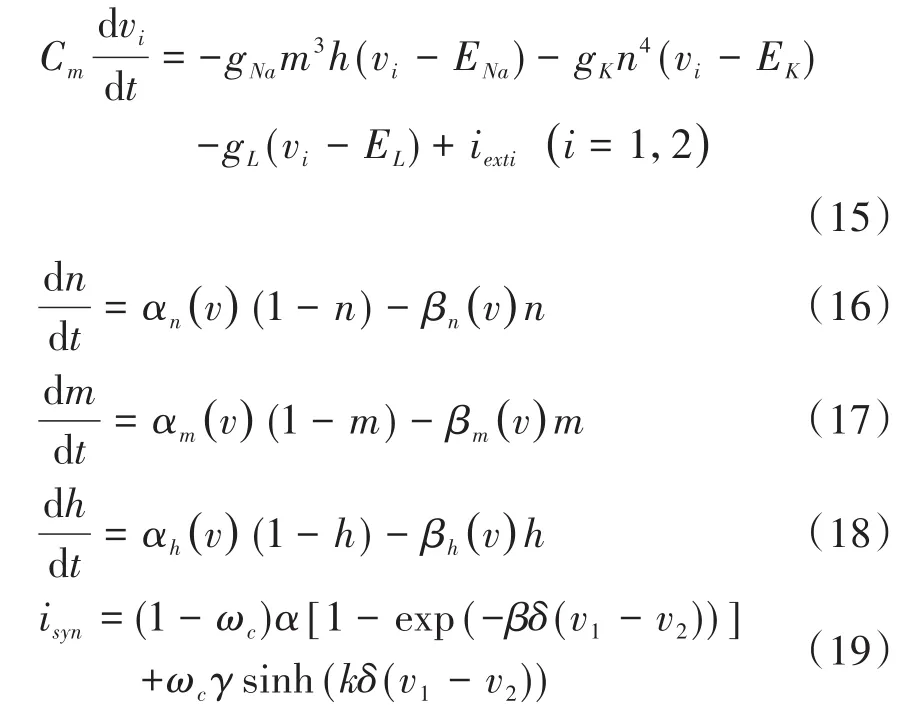
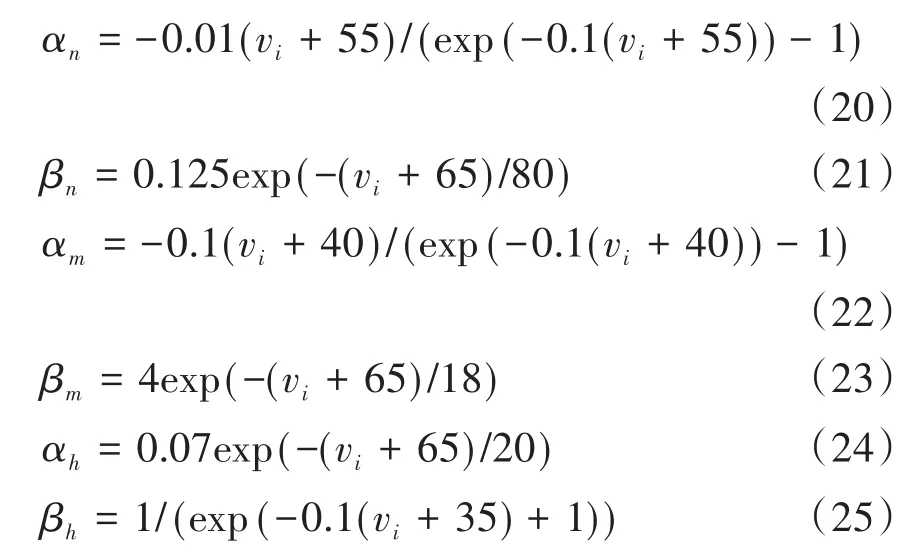
微分方程组中，v1和v2分别表示突触前和突触后神经元膜电位，iexti为外加刺激电流，isyn为突触电流，ωc为突触权重，正参数δ的引入是为了满足忆阻突触的工作电压范围.Cm为膜电容，gNa、gK分别为钠通道、钾通道最大电导，gL为漏电导；ENa、Ek、EL分别为钠通道、钾通道、漏通道的反转电势；m和n分别为钠通道、钾通道活化过程参数；h为钠通道失活过程参数.α函数和β函数是与膜电位有关而与时间无关的速率常数.

忆阻器是初值敏感元件，其电导率取决于历史电压和电流，不同初始值对突触后膜电位的影响十分显著.突触电流isyn随着忆阻突触权值初值ωc0的增大而增大，当外部刺激电流总和（iext2+isyn）超过8.8μA/cm2时，突触后神经元从静息态转变为周期峰放电状态［25］.当iext1=9μA/cm2，iext2=8μA/cm2，温度为300K时，突触后膜电位最大值随忆阻突触权值初值变化的响应图如图7所示.当初值在0.1至0.85之间变化时，突触后神经元膜电位处于阈下振荡状态，初值超过0.85之后，神经元处于周期峰放电状态.因本文主要研究温度对兴奋性突触后膜电位的影响，为了避免初值选取不当造成的干扰，将初值的选取范围控制在［0.1，0.8］之间.

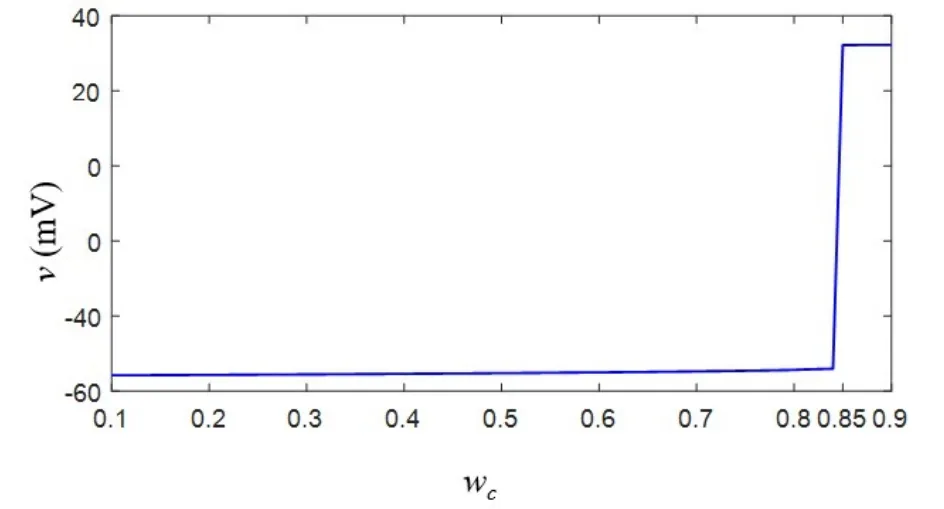
图7 突触后膜电位随忆阻突触权值初值变化响应图Fig.7 Response graph of postsynaptic membrane potential with initial value of memristive synaptic weight

当忆阻突触的初始权值ωc0取值0.3，iext1等于9μA/cm2，iext2等于 0μA/cm2，开关 S 处于打开状态时，突触前和突触后神经元放电状态如图8所示，在无突触电流输入情况下，突触后神经元自发放电之后一直保持静息电位.闭合开关S后，保持ωc0，iext1和iext2取值不变，温度取值依次为T=290K、T=310K和T=330K，突触后膜电位变化呈现如图9（a）-图9（c）所示的阈下振荡状态，随着温度升高，兴奋性突触后膜电位呈上升趋势.为进一步阐述温度对突触后膜电位的影响，设定温度在T=290K至330K之间递增，仿真得到突触后膜电位变化曲线，结果如图10所示.在低于室温时（290K-300K），此时兴奋性突触后膜电位升高不明显.当温度高于室温时（310K-330K），兴奋性突触后膜电位明显增大，该结果与高温下（29℃-37℃）大鼠海马组织切片中实测兴奋性突触后膜电位变化情况相一致［26］.因此，采用改进的温度依赖型忆阻器模型可研究高温对兴奋性突触后膜电位的影响，低温情况下与生理实验结果对比略显不足.

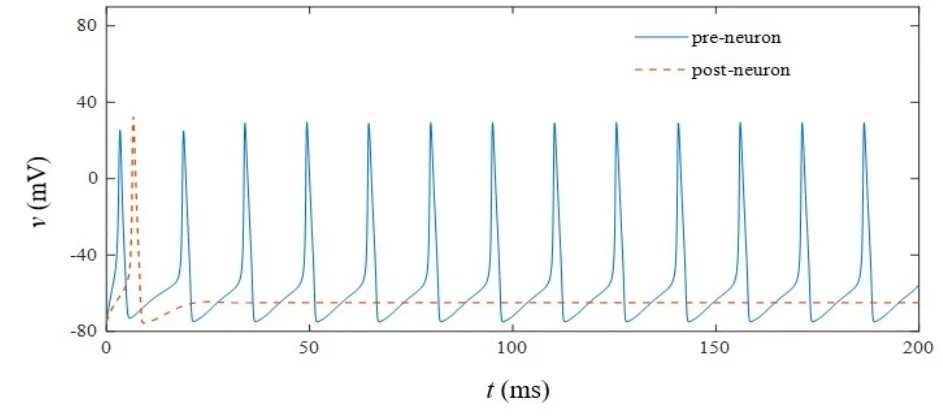
图8 开关S打开时突触前/后神经元的放电状态Fig.8 The firing state of pre/post-synaptic neurons when switch S is turned off

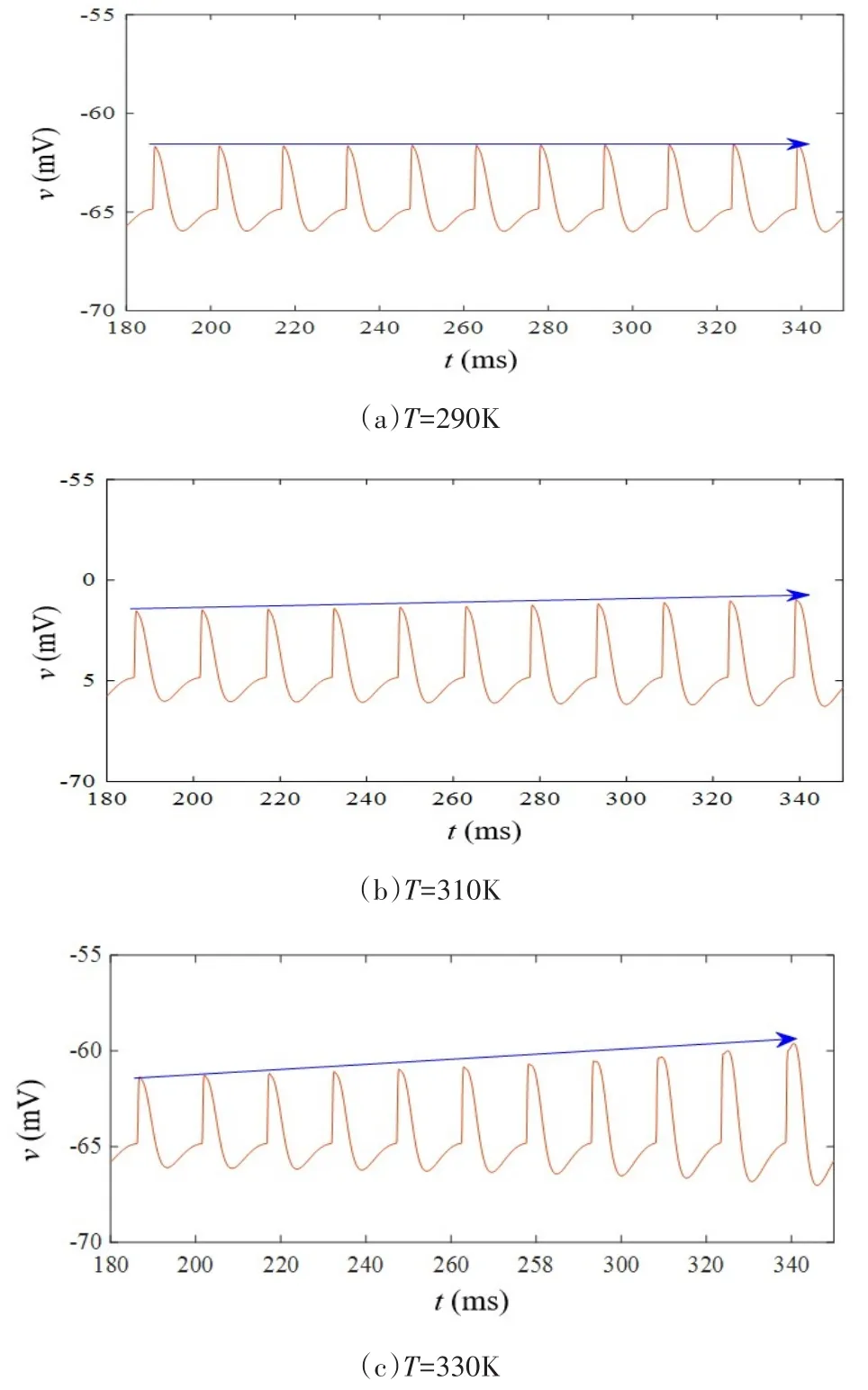
图9 不同温度下的突触后膜电位Fig.9 Postsynaptic membrane potential at different temperatures

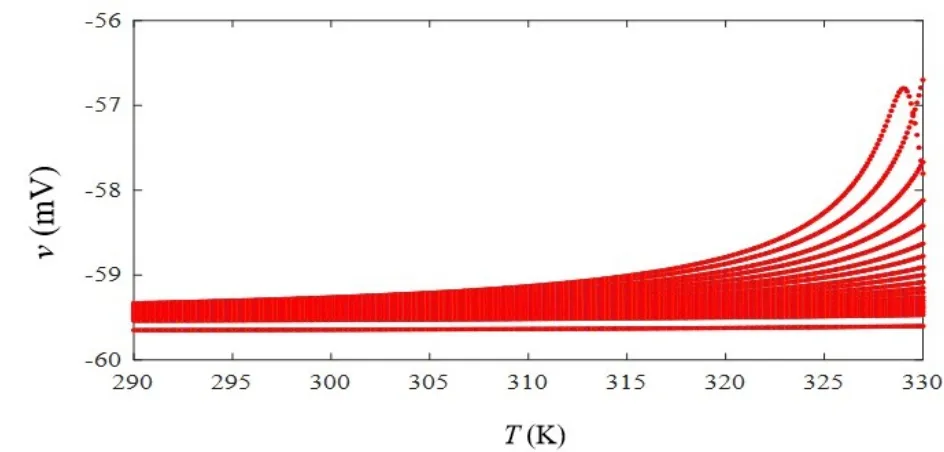
图10 不同温度下的突触后膜电位Fig.10 Postsynaptic membrane potential at different temperatures

当忆阻突触的初始权值ωc0取值0.65，iext1=15sin(0.001t)μA/cm2，iext2=14sin(0.001t)μA/cm2，开关S处于打开状态时，突触前神经元呈现周期性簇放电状态，突触后神经元经历短暂的簇放电状态之后转变为阈下振荡状态，变化情况如图11所示.开关S闭合后，温度取值依次为T=290K、T=310K和T=330K，突触后膜电位变化情况如图12（a）-图12（c）所示，随着温度升高，突触后神经元放电次数逐渐减少，该结果同样与生理实验现象相符［27］.

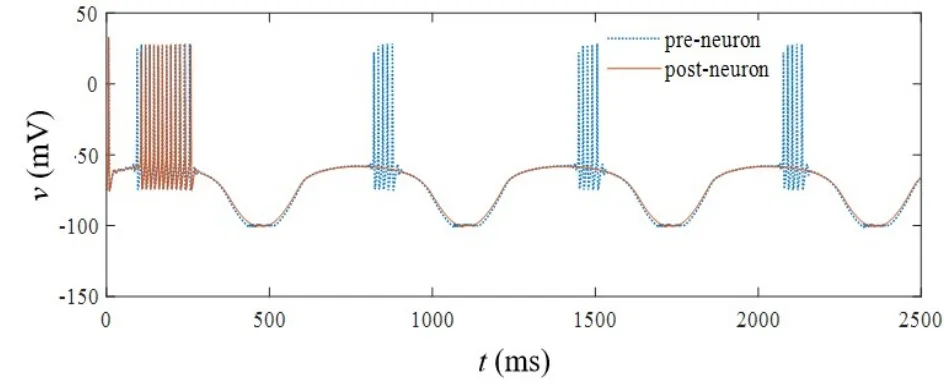
图11 开关S打开时突触前/后神经元的放电状态Fig.11 The firing state of pre/post-synaptic neurons when switch S is turned off

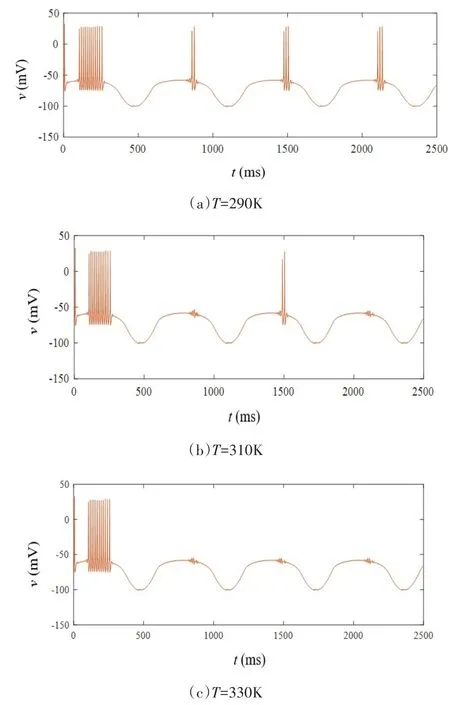
图12 不同温度下的突触后膜放电次数Fig.12 Number of postsynaptic membrane discharges at different temperatures

4 总结

本文在原氧化钨忆阻器数学模型的基础上，通过仿真呈现了其与忆阻器实测行为特性的差别，并考虑了温度对离子迁移和扩散的影响，基于此，引入了忆阻保留值ωcn和温度变量T.改进的模型不仅具有原模型的功能，并且可以拟合忆阻器的实际遗忘曲线以及符合同类型氧化物忆阻器的温度敏感特性.进一步，将此忆阻器作为生物突触耦合两个相同的HH神经元，通过对突触前后神经元施加不同的外部刺激电流，能够体现温度对突触传递的影响，即温度上升影响氧空位迁移和扩散速率，对应地引起兴奋性突触后膜电位的升高和放电次数的减少，数字仿真结果与神经生理现象相符.改进的氧化钨忆阻器模型更适合作为仿生突触应用到神经形态系统中，也为研究温度对突触传递的影响提供了一种新思路.