有界噪声激励下系统随机共振的改善*

张强 王剑龙 李扬 刘先斌

（南京航空航天大学航空学院，南京 210016）

引言

1981年意大利学者Benzi等在解释冰川周期时提出了随机共振理论［1］，指出非线性系统在同时受弱周期激励和随机激励时，噪声的能量会增强系统的周期输出，进而可以检测微到弱信号.随后，1983年Fauve和Heslot在研究Schmitt触发器时观察到随机共振现象［2］.1988年，McMamara、Wiesenfeld和Roy［3］在双向环形激光实验中也得到了类似的结果.此后，随机共振引起了国内外学者的关注，并在众多动力系统中均发现了该现象.例如Qin等［4］研究了二阶Duffing系统的随机共振，提出了一种快速迭代算法，该算法比传统算法具有更好的精度和收敛性.基于预测-校正方法，Yang等［5］学者研究了双稳态分数阶系统中的随机共振和随机P-分岔问题.当确定性系统的渐近状态是平稳的，Hu等［6］研究者揭示了一个有趣的现象，即随机共振也会出现在一个没有外部周期激励的系统中.类似地，没有噪声扰动但受周期性激励的Hodgkin-Huxley神经元也发现有随机共振现象［7］.近年来相关的研究仍有不少新的结果［8-11］.Han等［12］揭示了在Lévy噪声驱动下的多稳定系统中的随机共振机理，认为相比于双稳态或单稳态模型，多稳态模型中噪声对信号有更好的增强作用.Li等［13］基于SR理论提出了一种微弱信号检测方法，可用于风电设备故障诊断.

由于高斯噪声的无界性，它被认为不符合一些实际模型［14］.通常有界噪声被视为有色噪声的通用模型，其被定义为振幅恒定、平均频率恒定、相位满足单位维纳过程的谐波函数.有界噪声在物理、通信、化学、生物学等领域得到了广泛的研究［15-17］.Yung 等［18］研究了有界噪声驱动的 Fitzhugh-Nagumo神经系统中的随机共振，并通过数值计算表明，对于有界噪声，可以通过调整其噪声强度或颜色来诱导随机共振.在静态仿真的基础上，Fei等［19］.研究了非对称双稳态系统中有界噪声和周期信号引起的随机共振Zhao等［20］通过在激励中引入辅助高频信号，提出了一种利用振动强度改善随机共振现象的方法.尽管相关问题的研究目前已有了一些结果，但关于有界噪声强度与参数之间的关系及其对随机共振的影响尚没有特别的讨论.

本文内容如下：第一节，研究了受有界噪声扰动三个典型动力学系统的随机共振，考察参数改变对系统输出的影响；第二节，由于国内外关于随机共振的Simulink仿真实验较少［21］，因此通过建立Simulink模型来对系统进行模拟仿真，以验证第一节中有关结论的可靠性.

1 有界噪声的随机共振

我们考虑如下受有界噪声扰动和弱周期激励的Duffing随机共振双稳态模型

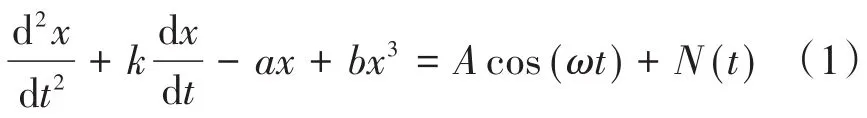
其中N(t)为有界噪声，如下所示

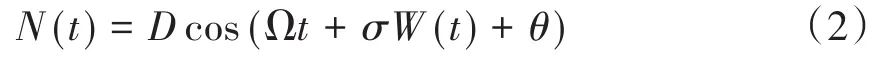
k为阻尼系数，σ为相位的随机程度，D与Ω分别是有界噪声的振幅和平均频率.θ满足[0，2π]上的一致分布，W(t)是单位维纳噪声，且有

其中ς(i)为高斯随机数.根据上述方程及高斯噪声的特性，方程（2）可写作

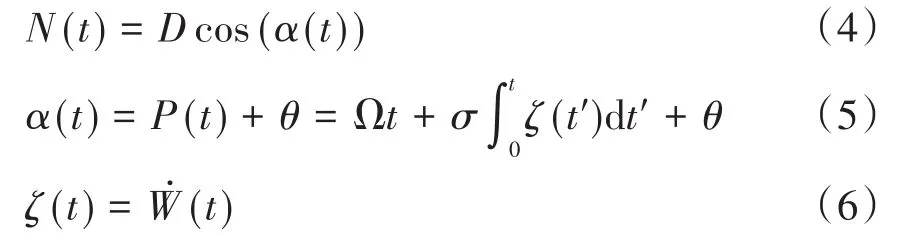
因此，α(t)均值及自相关函数为

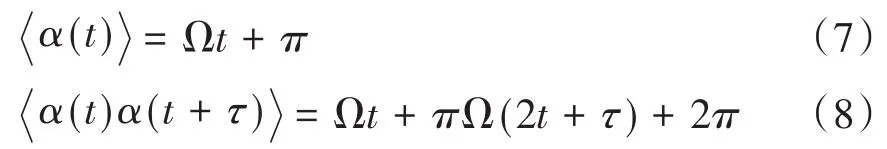
方程（2）的谱密度函数为

根据上式，方程（4）的均值及自相关函数可得

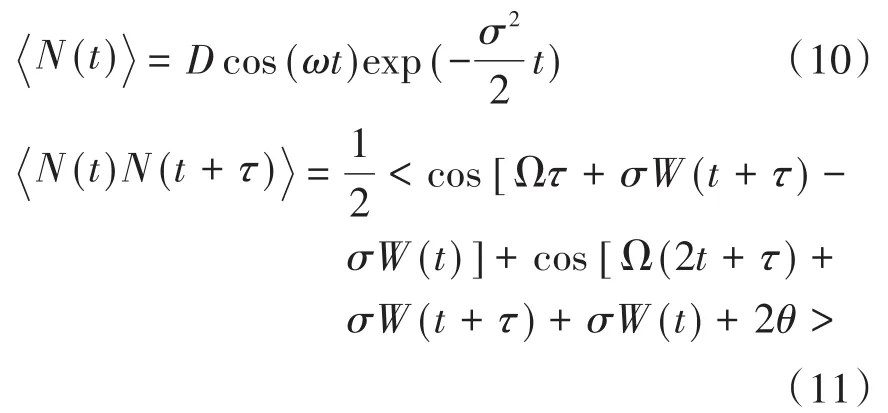
因此，有

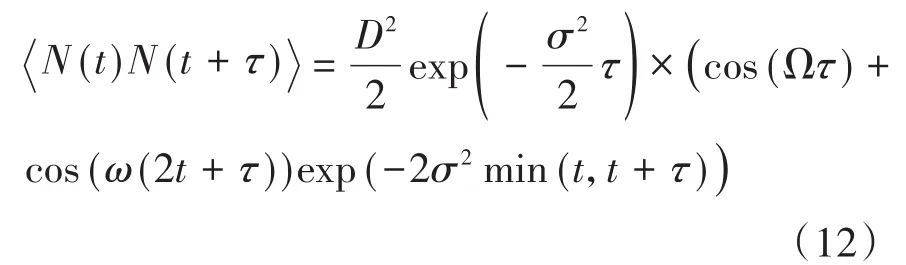
当t→ ∞时，方程（12）可简化为

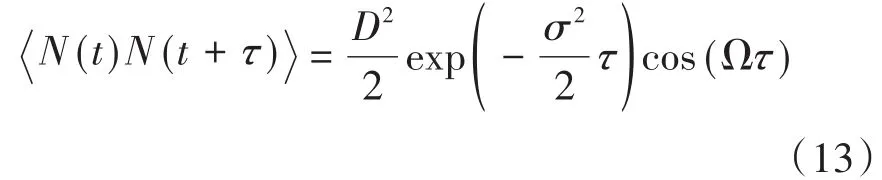
且可知其功率谱密度函数为

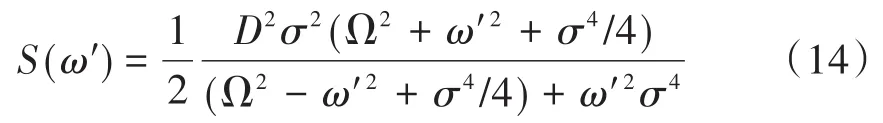
由上式可知，S(ω')依赖于参数D，σ和Ω.σ→ 0时，ω= ±Ω，有S(ω')→ +∞，在其他频率下，S(ω')→ 0.σ→∞时，有界噪声会无限近似于白噪声.

令

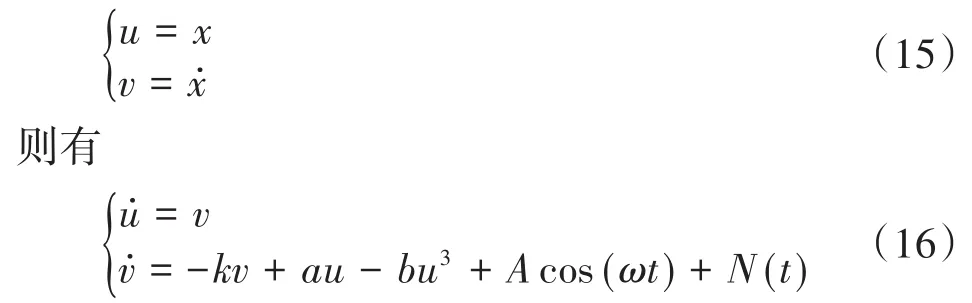
基于二阶随机Runge-Kutta法，对方程（16）离散可得

本文选择功率谱放大因子来衡量随机共振的效果，表达式如下所示

其中，A是外加弱周期激励的振幅，为了不失一般性，我们计算五百条路径，做傅里叶变换后再对其平均，得到.由于初始条件不影响计算结果，上述算法中均取为零.

我们分别取a=b=1，k=A=0.1，ω=0.1，0.3，σ=0.01，0.1，计算σ，ω，Ω改变时方程（1）的随机共振，来探究外部周期激励及有界噪声参数的改变对结果的影响.在计算时可发现结果具有较差的收敛性，尽管取方程（17）中的时间步长dt=0.001s，且考虑极长的时间历程，但σ=0.01时的计算结果仍然有所偏差.

从图1和图2我们可以看出ω与Ω满足一定数值关系时，系统随机共振的结果最佳（如图中黑色圆形标记所示）.不同Ω下峰值不断变化，但峰值所对应的D值相差不大，偏移较小.对比图1（a）与图1（b），图2（a）与图2（b），我们可以看出ω的增大会较明显的抑制随机共振的结果，且观察图2（b），Ω=0.1时，峰值处振幅相比于输入信号几乎不再具有放大效果.对比图1（a）与图2（a），图1（b）与图2（b）可知，σ的增大同样会抑制结果，但峰值的变化趋势和ω增大时相似，此外，在数值计算时我们发现，σ的增大会给系统结果带来更好的收敛性，所得到的曲线相比于σ=0.01时会更加光滑.

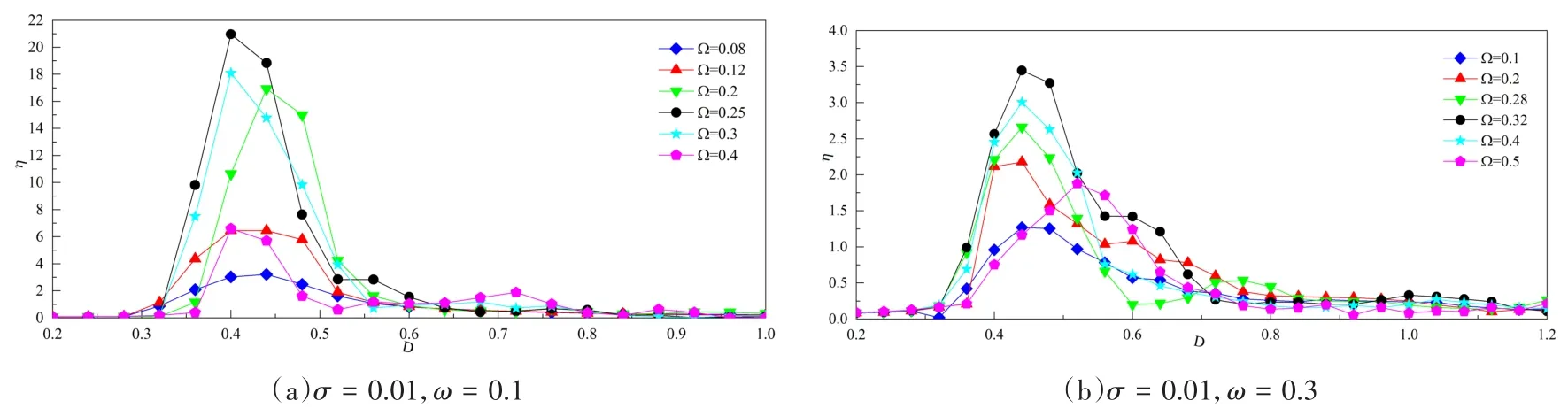
图1 方程（1）Ω改变时的D-η曲线Fig.1 D- η graph of Eq.（1）whenΩ changes

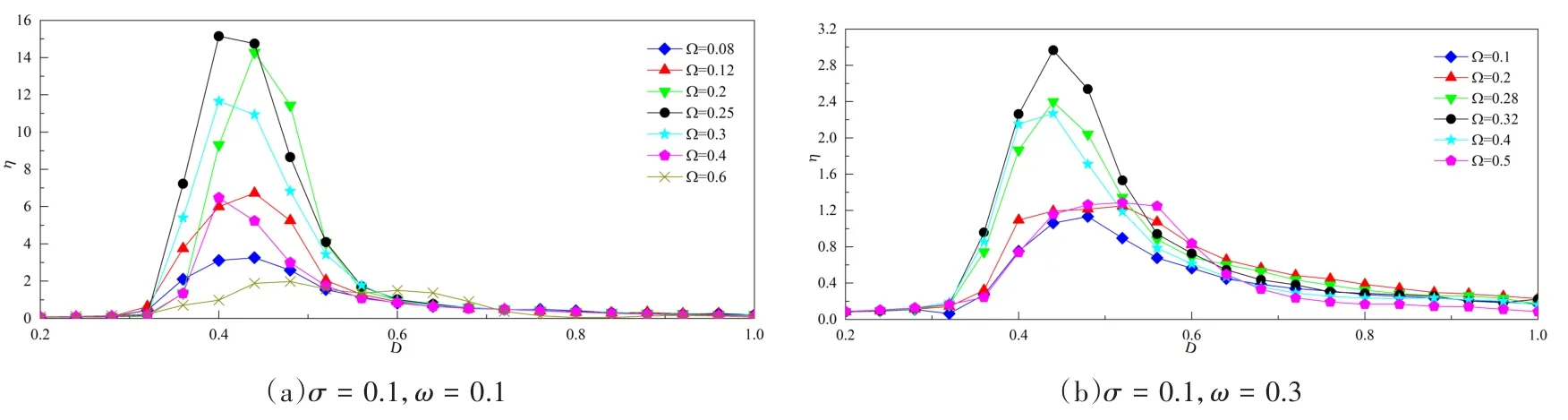
图2 方程（1）Ω改变时的D-η曲线Fig.2 D- η graph of Eq.（1）whenΩ changes

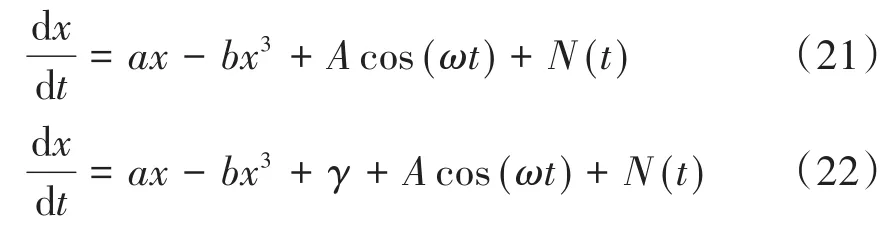
为了更好地探究σ-Ω的数值关系及σ，ω改变时分别对系统随机共振的影响，说明上述现象在有界噪声系统中存在的普遍性，我们再考虑如下两个Langevin方程：方程（21）是随机共振理论中经常研究的一维振子，具有势阱V(x)=-ax2/2+bx4/4，势能最小值在处取得.系统（22）在系统（21）的基础上加一个反对称参数γ，可以造成势阱的不对称性.这里我们取a=b=1，A=γ=0.1.

图3和图4是方程（21）的D-η曲线.与图1和图2对比可见，结果具有更好的收敛性.系统在Ω=0.5或Ω=0.8时随机共振的结果最佳，说明即使参数相同，在不同的系统中，ω-Ω的数值关系不尽相同.此外，在Ω不断增大的过程中，系统峰值并非只是减小，而是具有明显的偏移及其先增大后减小的过程.对比图3（a）与图3（b），图4（a）与图4（b），ω增大时，随机共振的结果被明显的抑制，对比图3（a）与图4（a），图3（b）与图4（b），σ的增大只会略微影响，和方程（1）的结果相近.系统（1）在Ω =0.5时，有ηmax≈ 1，观察图4-b可见，Ω =1.5时，仍有ηmax≥4，说明这系统（21）随机共振对信号的放大效果要远远优于系统（1）.

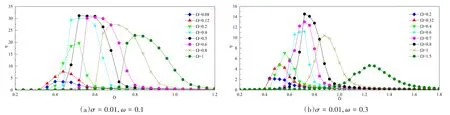
图3 方程（21）Ω改变时的D-η曲线Fig.3 D- η graph of Eq.（21）whenΩ changes

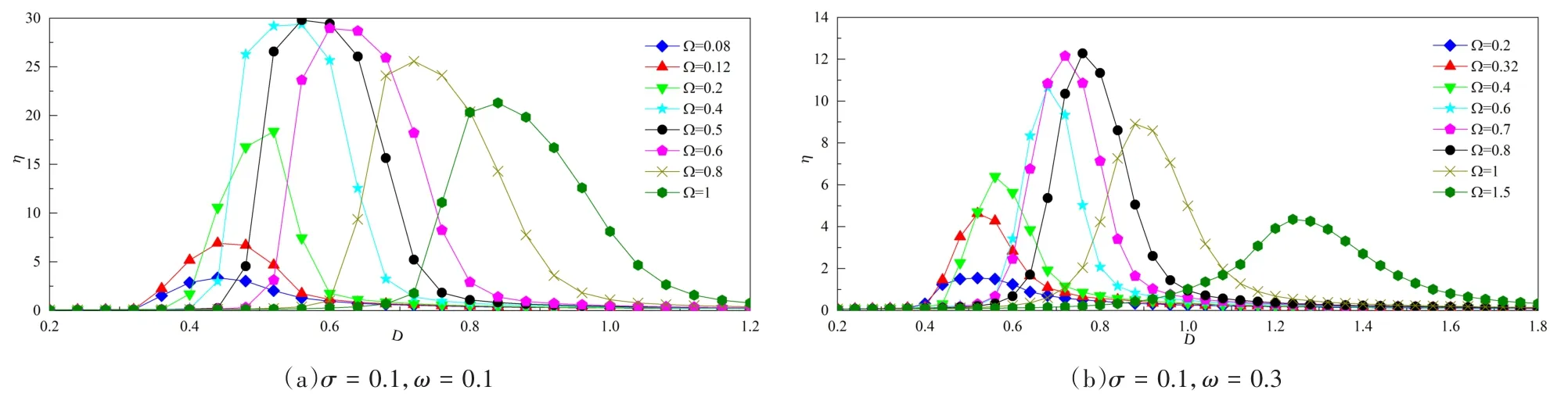
图4 方程（21）Ω改变时的D-η曲线Fig.4 D- η graph of Eq.（21）whenΩ changes

由于σ的微小增量对共振影响不大，为了更好的反应参数σ对结果的影响，计算方程（22）的随机共振时，我们取σ=1.图5和图6我们可以观察到与方程（1）和方程（21）相似的结果，但由于反对称参数的存在，随机共振的放大效果不如之前，这时更能体现ω和Ω的参数关系对系统的作用.此外，取不同参数时，分别在Ω=0.2，Ω=0.6，或Ω=1时随机共振的结果最佳，更加说明ω-Ω具有普遍性，但Ω增大时，各个系统所具有的峰值偏移效应却不尽相同.对比图5（a）与图5（b），图6（a）与图6（b），仍然可见ω的增大会抑制结果.对比图5（a）与图6（a），图5（b）与图6（b）可得，σ的显著增大会明显减弱放大效果，由于Ω≤0.22的结果近乎重合，图6（a）只给出了Ω =0.08，0.2，0.22的结果.观察图6（b）可知，尽管σ，ω的增大使得系输出的增幅小于输入信号，随机共振对于增强微弱信号的效果已不存在，但ω-Ω的数值关系仍然使系统输出存在最优值且峰值存在着偏移且先增大后减小的现象.

图5 方程（22）Ω改变时的D-η曲线Fig.5 D- η graph of Eq.（22）whenΩ changes

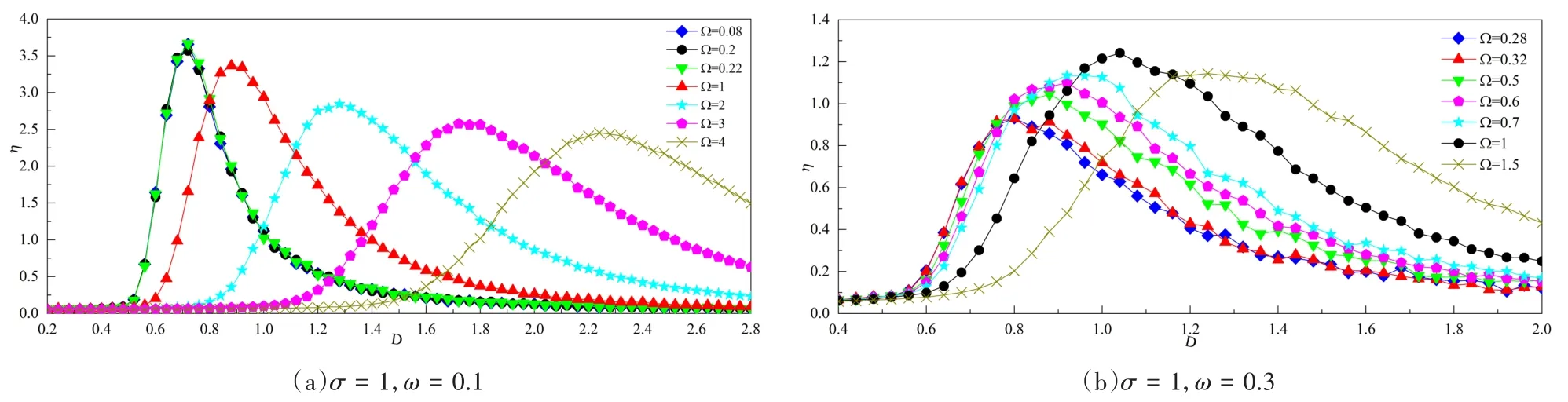
图6 方程（22）Ω改变时的D-η曲线Fig.6 D- η graph of Eq.（22）whenΩ changes

总结上述结果可知，不同系统中，σ，ω的增大往往会抑制随机共振，结果的峰值偏移效应不尽相同，但其大小变化趋势不变，总是呈现先增大后减小的趋势，也就是说，在Ω增大的过程中，会存在一实数n，使得Ω=nω时，系统随机共振的结果最佳，在类似于方程（21）这种随机共振所带来的放大效应不是很理想的反对称系统中，这一数值关系可以有效地改善输出.

2 随机共振的Simulink仿真研究

近些年来，在不同的领域中，关于随机共振的研究多局限于数值仿真、实验，模拟实验的研究较少，尽管模拟的数据相较于真实实验数据会有偏差，但是由于其简单易操作、节约成本、对真实实验结果具有预测性的特点，仍然具有一定程度的研究价值.这里我们便使用软件Simulink来验证上文结果在真实系统的存在性且验证ω-Ω这一数值关系对结果改善的可靠性.Simulink是Matlab中一种可以实现动态系统建模、仿真和分析的可视化工具，被广泛应用于线性、非线性系统，数字控制和数字信号处理的建模与仿真中.Simulink可以使用连续采样时间，离散采样时间或两种混合的采样时间进行建模，也支持多速率系统.通过建立模块方块图的图形用户接口（GUI），以更快捷、简洁明了的方式使用户更直观地看到系统的仿真结果.

这里我们建立方程（1）的仿真电路图，得到模拟实验的数据，采取同样的方式与其他参数，通过改变σ，ω，Ω，来探究随机共振的结果.

图7中，Bound noise为有界噪声，Sine Wave为外加弱周期激励，Integrator为积分器，D为有界噪声的振幅，x为输入到Matlab工作空间的仿真数据.为了不失一般性，我们通过m文件sim函数的反复调用，产生足够多的路径，经过离散傅里叶变换，再对结果进行平均，得到η.为了保证结果的收敛性，取很小的时间步长，仿真实验的时间历程也尽可能地长.

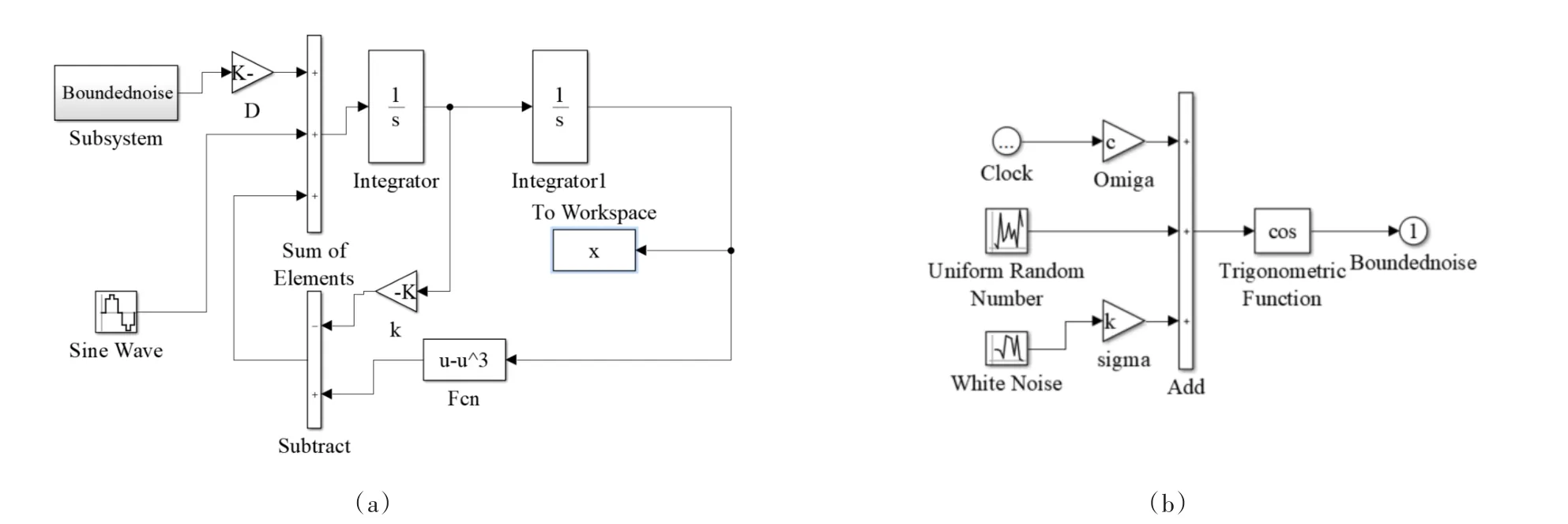
图7 方程（1）的Simulink仿真实验Fig.7 Simulation experiment of Eq.（1）

从图8和图9我们可以看出，与数值计算的结论相同，ω与Ω满足某一数值关系时，系统随机共振的结果最佳（如图中黑色圆形标记所示）.对比图1图2与图8图9，可以看出，由于系统的随机性，仿真实验的结果偏大，尽管得到的结果略微有差别，但误差在可以接受的范围内.通过Simulink的仿真，我们验证了这一数值关系的存在且可以明显改善系统随机共振的结果.

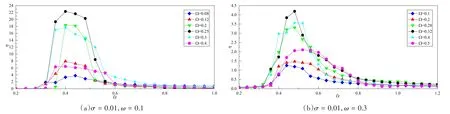
图8 方程（1）的Simulink仿真数据Fig.8 Simulation of Eq.（1）in Simulink

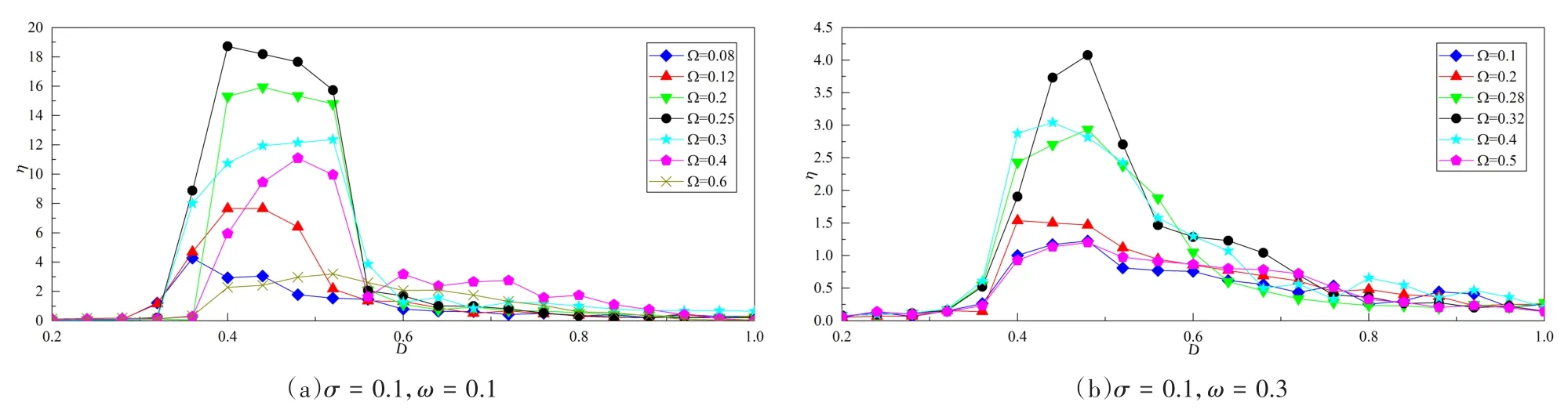
图9 方程（1）的Simulink仿真结果Fig.9 Simulation results of Eq.（1）in Simulink

3 结论

本文通过数值计算和仿真实验的方法研究了受有界噪声扰动及弱周期激励下三类典型系统的随机共振问题，探讨了平均频率Ω改变时有界噪声对共振结果的影响，发现当噪声频率与输入信号频率满足一定数量关系时，随机共振的放大效果最佳.尤其在特定系统中，通过调整有界噪声平均频率来增强共振结果是非常有效果的.