简谐激励下双弹簧非线性能量阱的优化*

王国旭 丁虎 陈立群

（上海大学力学与工程科学学院，上海 200444）

引言

振动在日常生活中是一种常见的物理现象.很多时候人们不希望机器发生振动，因为振动会产生噪声、降低使用寿命和给人体造成不适，为此人们致力于通过各种方式抑制有害的振动.

现有的振动控制方式主要分为主动控制、半主动控制和被动控制.相比以智能材料和控制算法为特征的主动和半主动控制［1-3］，被动控制由于具有结构简单、节能省材和不需人为控制等优势，广泛受到关注.吸振器是一种常用的减振手段.传统的被动式吸振器如调谐质量阻尼器或线性吸振器（Linear Vibration Absorber，LVA）广泛应用于各种系统的振动抑制，比如U型梁和风力机结构的振动控制［4，5］.LVA由质量块、阻尼器和弹簧组成，结构简单，但只能在较窄的频带内有振动抑制作用，而且会使系统产生新的共振峰.为了弥补LVA的不足，Chen等［6］在吸振器中引入非线性刚度，实现零线性刚度和多模态减振，并保持原系统的共振频率.这种吸振器称为非线性能量阱（Nonlinear Energy Sink，NES）.

Gendelman 等［7］和 Vakakis等［8］是研究 NES 的先驱，他们将立方NES耦合到线性系统，在瞬态激励下使能量不可逆地从线性系统转移到NES，这种现象称为能量靶向传递（Targeted Energy Transfer，TET）.Jiang等［9］在扫频简谐激励的结果中发现，NES可以在相当宽的激励频率范围内吸收较多的振动能量.Gendelman等［10］和Starosvetsky等［11］的成果表明NES在强调制响应下可以实现比周期响应更好的振动抑制效果.Gourdon等［12］在实验中通过双弹簧结构实现了立方NES，并研究了地震激励下立方NES的表现，说明相比LVA，NES可以在小质量条件下有更好的表现.然而，Gourdon等［12］也指出，NES只在大激励条件下才有较好的减振效果.

为了拓宽NES减振所需的能量条件，ALShudeifat［13］提出了双弹簧结构的双稳态 NES.与零刚度立方NES不同，双稳态NES具有负刚度.ALShudeifat［13］的成果表明在瞬态激励下双稳态NES可以在更大的初始能量范围内实现比立方NES更好的振动抑制效果.Romeo等［14］进一步揭示了瞬态激励下双稳态NES的TET实现方式，即大激励条件下的非线性拍振和小激励条件下的阱间混沌运动.Qiu等［15］通过解析方法拓宽了双稳态NES在简谐激励下发生强调制响应的激励范围，提升了NES的减振性能.为改善双稳态NES阱内运动的表现，Habib等［16］参照LVA设计了一种调谐双稳态NES.近年来，许多学者致力于双稳态NES的结构设计，比如屈曲梁和永磁结构［17-19］.

以上简要介绍了线性和非线性吸振器的特点，实际中我们需要确定吸振器的最优减振效果及参数配置，以此发掘它的潜在应用价值.另外，由于制造误差和环境等因素，吸振器的参数会有微小波动，此时需要找到吸振器的较优减振效果及参数配置，评价其鲁棒性.因此，本文将通过差分进化（Differential Evolution，DE）算法和参数分析优化简谐激励下能实现立方刚度和双稳态特点的双弹簧NES，并对比LVA，说明两者的区别和联系以及NES的应用价值.

1 力学模型

本文研究的单自由度线性振子（Linear Oscillator，LO）附加双弹簧NES模型如图1所示，系统定常参数如表1所示.M2、C2和KS为NES的质量、阻尼和刚度.L1和L2为NES两个方向上的特征长度.X1和X2为LO和NES的位移.F0和Ω为激励幅值和频率.通过调节LO两端支架的距离2L1，双弹簧NES可以实现单稳态（L1≥L）或图1中的双稳态（L1＜L）.

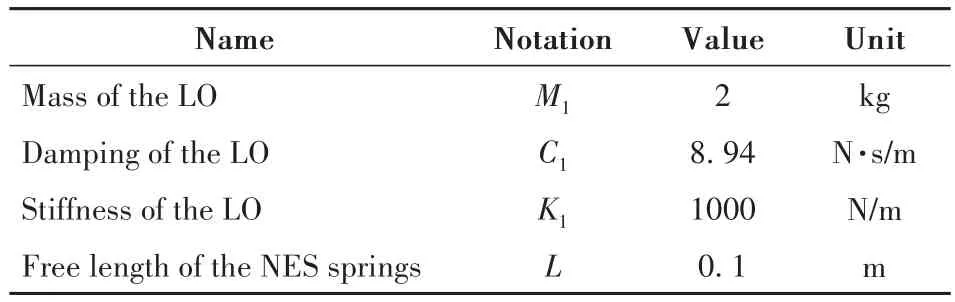
表1 系统固定参数Table 1 Fixed parameters of LO-NES system

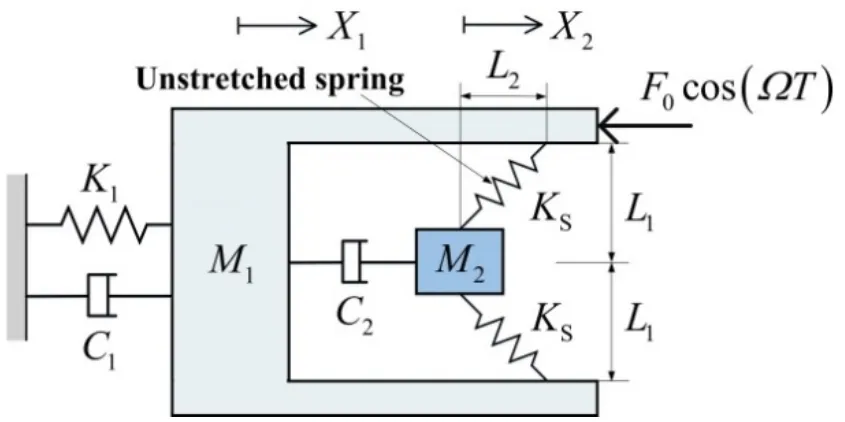
图1 LO附加双弹簧NES的力学模型Fig.1 Model of LO with NES

利用牛顿第二定律，系统控制方程可以写为

其中T为时间.方程（1）的无量纲形式为

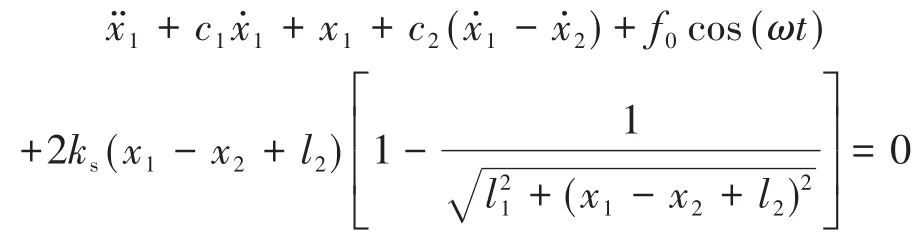
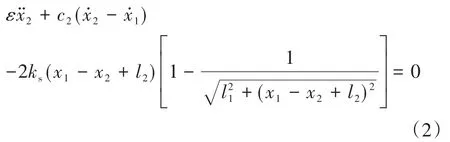
其中（·）表示对无量纲时间t求导.各无量纲参数和变量的表达式为

本文将参照LVA的结果衡量NES的减振效果，由于LO附加LVA系统的无量纲参数表达式与LO附加双弹簧NES系统的一致，方便起见，将ε、c2、ks和x2统称为吸振器的无量纲质量、阻尼、弹簧刚度和位移.由于NES在简谐激励下会存在准周期、强调制和混沌运动，传统的半解析方法（比如摄动法和广义谐波平衡法）不能准确预测这些响应的时间历程，而Runge-Kutta法可以，因此本文将利用Runge-Kutta法得到的结果对NES进行优化.设定Runge-Kutta法的计算时长为100个周期，时间步长为一个周期的1/200，截取时程末尾的周期个数为20，在所有的激励频率下系统位移和速度初值均为0，激励频率ω的变化范围和步长为0.8～1.2和0.02.

2 优化方法与问题描述

DE算法通常被用来求非线性、不可微问题的最优解，具有速度快、鲁棒性好的特点.本文将采用DE算法优化双弹簧NES的四个参数（ε、c2、ks和l1）和LVA的三个参数（ε、c2和ks），其流程图如图2所示.经收敛性验证和参考文献［20］，设定DE算法中的种群规模为40，最大迭代次数为100，变异因子为［-2，2］均匀分布的随机数，交叉概率为0.9.由于DE算法以一定概率收敛到全局最优解，故对同一优化问题进行20次试验，保留最优结果.本文将通过LO扫频区间的稳态位移振幅最大值作为衡量吸振器减振效果的依据，优化目标即最小化LO在扫频区间的振幅最大值.本文也将通过参数分析方法验证DE算法的结果.

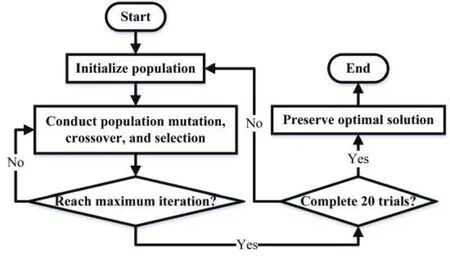
图2 DE算法流程图Fig.2 Flow chart of DE algorithm

3 数值算例

本文关注小质量吸振器在扫频简谐激励下的表现，吸振器的参数优化范围为10-5≤ε≤0.02、10-5≤c2≤10、10-5≤ks≤10 和 10-5≤l1≤2.表 2展示了小和大激励幅值下两种吸振器优化参数和最大振幅衰减率RA的结果.RA为有吸振器时LO在整个频域内最大振幅max（ALO）相对无吸振器时LO最大振幅max(A'LO)的衰减率，其表达式为

表2的结果表明LVA和NES对LO扫频最大振幅的最优抑制效果、优化质量和阻尼值几乎相同，且NES的最优抑制效果不受激励幅值的影响.在NES弹簧刚度ks和几何参数l1的优化结果上，随着l1越远离1，ks的值越小.小激励条件下，最优NES的ks大于最优LVA的ks，最优NES的l1分布范围较广；大激励条件下，最优NES的ks与最优LVA的ks差别较小，最优NES的l1趋近于其上限值.

接着我们通过参数分析验证DE算法的结果，比较NES和LVA较优减振效果对应的参数范围.图3为最优质量比条件下不同LVA阻尼和弹簧刚度的LO振幅衰减率结果，其最优减振效果与表2中的数据基本重合.图4为最优质量比和阻尼条件下不同NES阻尼和弹簧刚度的LO振幅衰减率结果，相比LVA，NES可以在较大的弹簧刚度范围内实现较优的减振效果，尤其是NES接近单稳态弹簧无伸长状态的时候（l1=1）.另外，图4的结果表明激励幅值会对NES的较优参数区域有巨大的影响.在小激励幅值下，双稳态（l1＜1）和单稳态（l1＞1）NES均能实现很好的减振效果；而在大激励幅值下，较优的减振效果主要通过单稳态NES实现.图4中NES的最优减振效果及其参数特点也能很好地吻合表2中DE算法的结果.

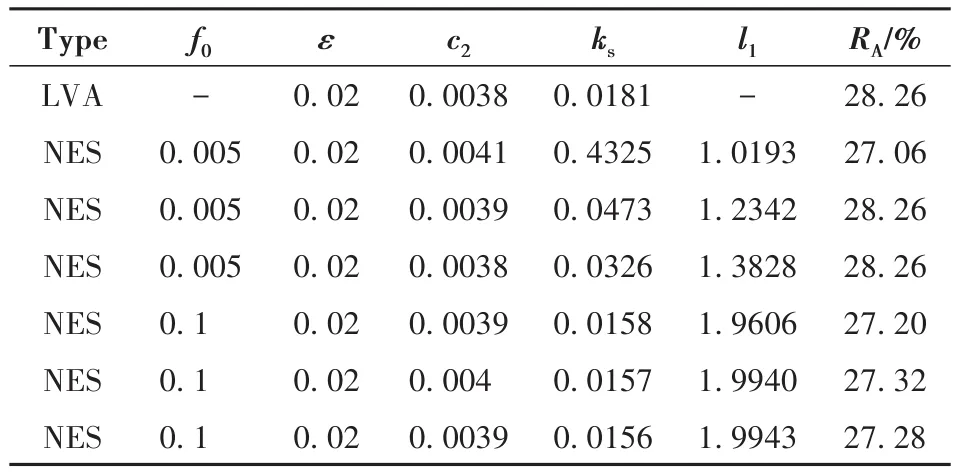
表2 DE优化算法结果Table 2 Results of DE algorithm

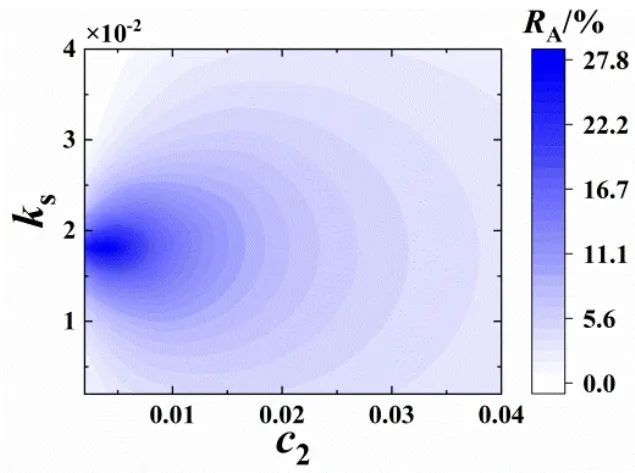
图3 ε=0.02时振幅衰减率随LVA阻尼和弹簧刚度的变化关系Fig.3 Amplitude decaying rate of with varied damping and spring stiffness of LVA and ε=0.02

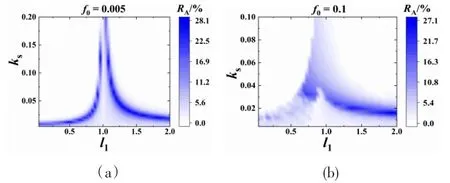
图4 ε=0.02和c2=0.004时振幅衰减率随NES几何参数和弹簧刚度的变化关系：（a）f0=0.005；（b）f0=0.1Fig.4 Amplitude decaying rate of with varied geometry parameter and spring stiffness of NES，ε=0.02，and c2=0.004：（a）f0=0.005；（b）f0=0.1

进一步我们选取两种典型的NES几何构型，即双稳态和单稳态弹簧无伸长NES的减振效果在两种激励幅值下随NES阻尼和弹簧刚度的变化关系，如图5和图6所示.结果表明，在大多数情况下，NES的减振效果会同时受阻尼和弹簧刚度的影响，而图5（b）中单稳态弹簧无伸长NES在小激励幅值下的减振效果与弹簧刚度基本无关.这是因为处于单稳态弹簧无伸长状态的NES控制方程在小激励幅值下可以通过Taylor级数展开成零线性刚度和立方刚度的形式，此时NES不需要通过刚度调谐实现较优的减振效果，但此时的减振效果不及最优LVA和其他几何参数下的最优NES.在大激励幅值下，由于NES响应较大，其控制方程的解不在Taylor级数的收敛域内，此时单稳态弹簧无伸长NES不具有零刚度特性，需要通过刚度调谐实现较优的减振效果.这也是图6两种NES结果非常接近的原因.由于本文研究的NES具有线性阻尼，与LVA一样，NES也需要通过阻尼调谐实现较优的减振效果.

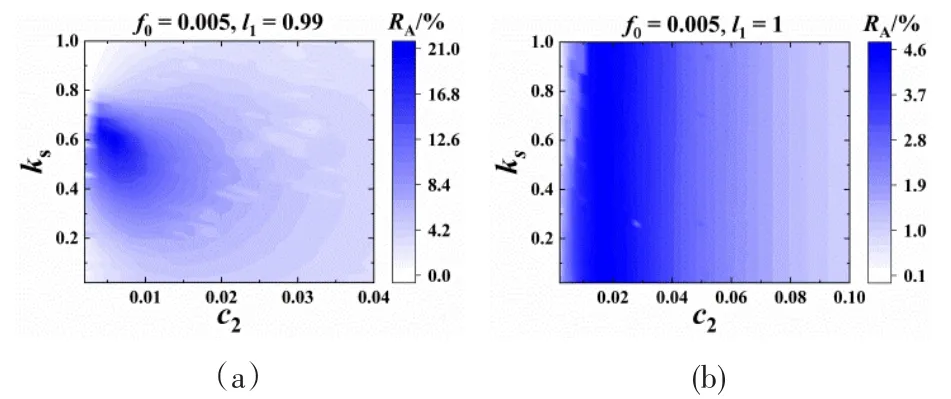
图5 ε=0.02和f0=0.005时振幅衰减率随NES阻尼和弹簧刚度的变化关系：（a）l1=0.99；（b）l1=1Fig.5 Amplitude decaying rate of with varied damping and spring stiffness of NES，ε=0.02，and f0=0.005：（a）l1=0.99；（b）l1=1

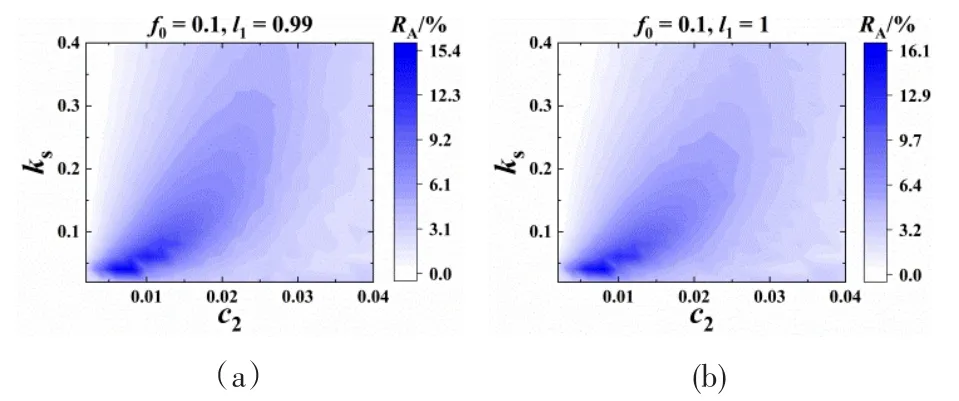
图6 ε=0.02和f0=0.1时振幅衰减率随NES阻尼和弹簧刚度的变化关系：（a）l1=0.99；（b）l1=1Fig.6 Amplitude decaying rate of with varied damping and spring stiffness of NES，ε=0.02，and f0=0.1：（a）l1=0.99；（b）l1=1

以上讨论了LVA和NES的参数优化特点，那么优化后系统的响应会是怎样的呢？图7和图8解答了这个问题.ALVA和ANES分别表示LVA和NES的稳态位移振幅.图7和图8中LVA的参数为表2中的数据，NES的参数为图5和图6中的最优参数，每个激励频率下LO和吸振器的初始位移和速度均为0.图7和图8的结果表明，在小和大激励幅值下，NES对应的最优LO响应接近LVA对应的最优LO响应，即LO均存在两个较为平缓的峰值，吸振器的共振频率略低于LO的固有频率.而小激励幅值下的单稳态弹簧无伸长NES由于具有零刚度特性，此时LO和NES的共振频率仍为无NES时LO的共振频率，但减振效果不明显.图7和图8的结果还说明，对LO的振动抑制主要通过较大的吸振器振幅实现，为了保护较大激励幅值下的吸振器，需要对其引入限幅装置，但此时减振效果需要进一步核实和优化.另外，激励幅值的大小不仅会影响NES参数的较优区域，也会影响系统的幅频响应，尤其是NES的幅频响应和双稳态NES的运动特性.具体来说，在大激励条件下，NES在低频区和高频区的幅值较小，而共振区存在幅值的突弹跳变现象，这种现象不会发生于小激励条件.结合双稳态NES两个稳定平衡点之间的距离2l2，可以说明双稳态NES在小激励条件下通过阱内运动实现全频域的最优减振效果，在大激励条件下图8（a）两条竖直点线所围成共振区内双稳态NES的运动形式为阱间运动，而在低频区和高频区内双稳态NES的运动形式仍为阱内运动.

图7 ε=0.02和f0=0.005时LO、最优LVA和NES的幅频响应：（a）l1=0.99；（b）l1=1Fig.7 Frequency response of LO and optimal LVA and NES with ε=0.02 and f0=0.005：（a）l1=0.99；（b）l1=1

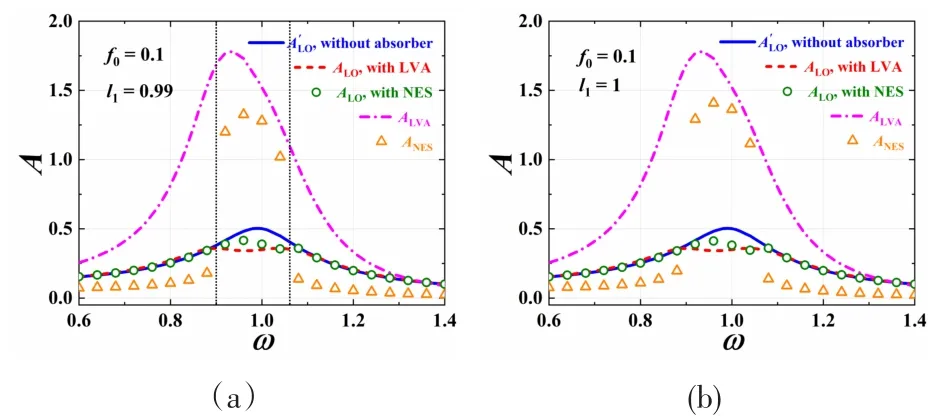
图8 ε=0.02和f0=0.1时LO、最优LVA和NES的幅频响应：（a）l1=0.99；（b）l1=1Fig.8 Frequency response of LO and optimal LVA and NES with ε=0.02 and f0=0.1：（a）l1=0.99；（b）l1=1

4 结论

通过DE算法和参数分析优化简谐激励下的LVA和双弹簧NES，主要结论如下：

（1）最优LVA和最优NES在对LO扫频最大振幅的抑制效果、质量和阻尼大小上无明显差别.

（2）相比LVA，NES可以在较大的弹簧刚度范围内实现较好的减振效果.

（3）激励幅值对NES最优抑制效果的影响不大，但对NES较优参数区域和幅频响应的影响很大.

（4）零刚度NES适用于小幅激励，减振效果不及最优LVA和双稳态NES，但不改变系统共振频率.