一类发展方程指数吸引子的存在性

2022-01-06柳映堂

湖南文理学院学报(自然科学版) 2021年4期

关键词：定性常数全局

柳映堂

(长沙理工大学数学与统计学院,湖南长沙,410001)

本文主要讨论如下带记忆项非经典扩散方程

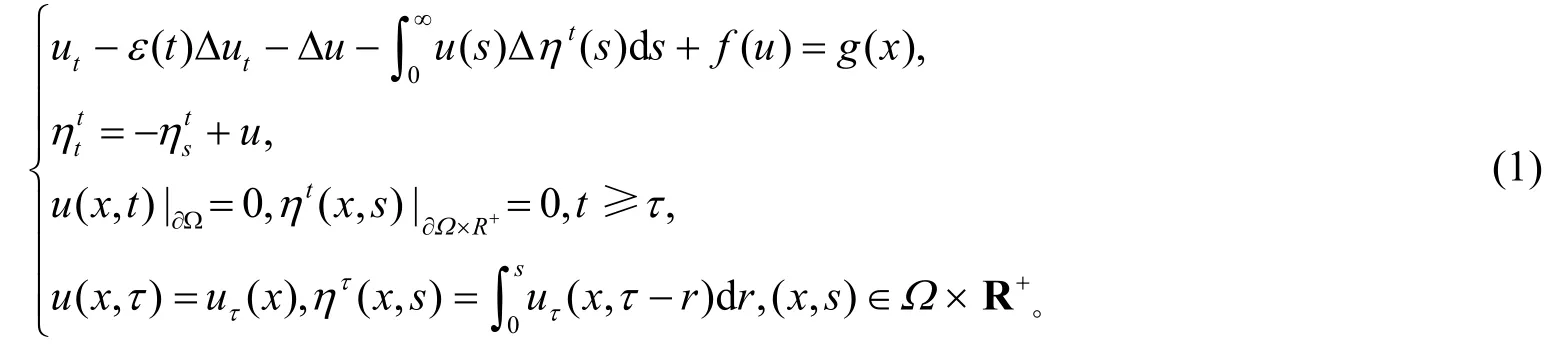
的渐近行为。其中Ω∊Rn(n≥3)是带有光滑边界的有界域,τ∊R是初始时间,记R+=(0,∞),时滞项u(t-s)假设为

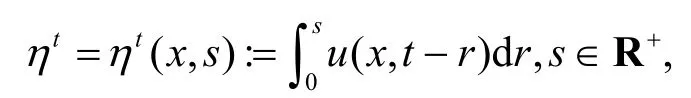
外力项g=g(x)∊H-1(Ω)；ε(t)∊C1(R)为单调递减有界函数,且此外，存在常数L>0,使得。

对核函数k(s)和非线性项f,可做如下假设

(H1)核函数k(s):令μ(s)=-k′(s),设μ∊C（1R+)∩L（1R+),μ(s)≥0,μ′(s)≤0,∀s∊R+,且存在δ＞0,使得

其中M＞0为常数且σ≤δ(δ来自于式(2))。

方程(1)主要被用于流体力学,固体力学以及热传导理论等领域[1–2]。其与通常的反应扩散方程相比,主要考虑了粘弹性和u过去历史的影响(例如聚合物,高粘性流体等[3]);当前述情况都被包含时,才会形成带有记忆项的非经典发展方程(1)。

当方程(1)中核函数k(s)=0且时间依赖参数ε(t)为常数时,相应方程的适定性及其解的渐近行为已被许多学者所考虑(见文献[4–10]及其参考文献)。特别地,在文献[11]和[12]中,当非线性项分别满足|f′(u)|≤c(1+|u|)和临界指数增长时,作者得到了Ht上时间依赖全局吸引子的存在性。文献[13]研究了不带记忆项的非经典扩散方程,在非线性项满足任意阶指数增长情况下,得到了方程的适定性以及时间依赖全局吸引子的存在性。但对满足任意阶多项式增长情形时方程(1)时间依赖指数吸引子的存在性还未见研究。

因此,本文主要对方程(1)时间依赖空间上指数吸引子的存在性进行研究。由于非线性项满足任意阶多项式增长且方程(1)中含有记忆项,从而导致Sobolev嵌入是非紧的,故将充分利用加强的平坦性条件以及分析技巧克服上述困难,进而得到了时间依赖指数吸引子的存在性。