一类克莱因瓶网络的完全独立支撑树

王志颖，魏二玲

(中国人民大学 数学学院, 北京 100872)

0 引 言

信息社会离不开计算机互联网络. 随着互联网使用规模的不断扩大, 处理器之间的连线故障更加频繁.为此, 网络需要具备一定的容错性.网络的容错性是指在故障发生时, 网络是否能继续保持良好的性能.反映到理论上, 就是要对互联网络拓扑结构的研究.多处理器系统可以用一个图网络来表示.多处理器即图中的节点, 两个多处理器之间若有线相连, 即在两点之间连边.多处理器故障即网络的顶点故障, 连线故障即边故障.完全独立支撑树被广泛应用于互联网的容错通信问题之中.当计算机沿着这k个完全独立支撑树发送消息时, 即使k-1个支撑树路径发生故障, 最后一个支撑树路径仍然能保证通信过程正常进行，所以对完全独立支撑树的研究是非常有意义的.

完全独立支撑树的研究是源于Hasunuma[1]的早期工作，作者给出了完全独立支撑树的刻画并证明了k连通线图的基础图存在k个完全独立支撑树.Araki[2]、Hong和Liu[3]以及林政宽等人[4]关注图的最小度条件，给出了存在完全独立支撑树的新的充分条件.Hong[5]证明了最小度δ≥k、顶点数n≥2k的连通图G的k次方图Gk存在k个完全独立支撑树.Qin等[6]给出了一类复合图存在k个完全独立支撑树的充分条件.判断图是否存在完全独立支撑树，除了从最小度数条件出发, 还可以从图的连通度出发.Hasunuma[1]进一步研究了完全独立支撑树与连通度之间的关系,猜想任意2k连通的图都有k个完全独立支撑树.Péterfalvi[7]和Pai等人[8]证明了这个猜想是不正确的，并且Péterfalvi[7]给出了反例，表示对任一个k(k≥2)，存在k连通的图，但图中找不到两个完全独立支撑树.说明连通度不是保证存在完全独立支撑树的条件.更多关于完全独立支撑树的研究可参见文献[9]和[10]等.

虽然Hasunuma的猜想存在反例，但是仍有大量的2k连通的图有k个完全独立支撑树，尤其对一些具有高度对称性的网络.文献[11]证明了对任一个环面网络来说，都存在两个完全独立支撑树.很多大型并行计算机中大量采用环面平行互联网络.本文讨论的一类克莱因瓶网络是环面网络的一种变形.它是一个具有mn个顶点,2mn条边的图.我们知道一个mn个顶点的树含有mn-1条边, 由边的关系我们知道这类网络的完全独立支撑树至多有两个. 在接下来的讨论中, 我们将集中讨论这类网络是否存在两个完全独立支撑树.

1 预备知识

首先我们给出本文讨论的克莱因瓶网络K(m,n)=(V,E)的定义, 其中m和n是大于等于3的整数，其顶点集为V={(i,j)|0≤i≤m-1,0≤j≤n-1},((i,j),(s,t))∈E当且仅当满足以下三种情况之一：

①i=s,j≡t±1(modn)；

②j=t,i∉{0,m-1}或s∉{0,m-1},i≡s±1(modm)；

③i,s∈{0,m-1},i≠s,j+t=n-1.

图1给出了K(m,n)的图示.为了使图清晰起见，本文对部分边使用半边表示法，即一条边分解为两个半边.例如：图1中顶点(0,0)和(m-1,n-1)关联的两个半边合起来即为边((0,0),(m-1,n-1)).在之后所示的图中，我们都采用了这种表示法，不再赘述.

图1 克莱因瓶网络K(m,n)Fig.1 Klein bottle network K(m,n)

文献[11]中将并行计算中用到的一类网络称为环面网络，并讨论了环面网络的完全独立支撑树图.本文讨论了与文献[11]中网络类似、但对称性稍弱、可以嵌入在克莱因瓶上的网络, 并定义其为克莱因瓶网络.图2给出了以K(3×4)在克莱因瓶上的嵌入.

图2 K(3,4)在克莱因瓶上的嵌入Fig.2 Embedding of K(3,4) on the Klein bottle

接下来介绍第二个重要的定义：完全独立支撑树(CIST). 设G是一个简单无向图,P1和P2是图G中顶点x到顶点y的两条路, 如果P1和P2除了顶点x和顶点y以外没有相同的顶点和边, 那么称P1和P2是内部不相交的.设T1,T2，…，Tk是图G的一组生成树，对图G中的任意两个顶点r和v, 如果T1,T2，…，Tk中顶点r到顶点v的路两两内部不相交, 那么称T1,T2，…，Tk是图G的一组完全独立支撑树.

①图G的任意导出子图G[Vi]是连通的；

②二分图B(Vi，Vj)的每一个连通分支H满足|E(H)|≥|V(H)|,i=1,2,3，…，k且i≠j.

定理1.1[1]连通图G有k个完全独立支撑树，当且仅当G的顶点集V(G)存在CIST划分(V1,V2,…，Vk).

定理1.2[1]设T1,T2，…，Tk是图G的一组生成树，T1,T2，…，Tk是一组完全独立支撑树当且仅当T1,T2，…，Tk是边不相交的, 并且图G中任意顶点v仅在最多一个生成树Ti中满足dTi(v)>1.

2 克莱因瓶网络的完全独立支撑树

定理：K(m×n)有两个完全独立支撑树，这里m≥3,n≥3.

证明：我们将用红、蓝两种颜色对边进行染色, 之后将点按照其关联的多数边的颜色染色.我们将证明所有红(蓝)边导出K(m×n)一棵支撑树，并且这两棵支撑树是完全独立的，从而该定理得证.下面按照参数的奇偶性，将K(m×n)分为三类，然后依次进行证明.

(1)K(2k×n),k≥2,n≥3的染色规则：

1)给下列集合中的边染为红色：

2)给下列集合中的边染为蓝色：

3)不染色的边有两条：

((0,0)，(2k-1,n-1))以及((0,n-1),(2k-1,0)).

图3给出了按照上述方法所得的染色.

图3 K(2k×n),k≥2,n≥3的一组完全独立支撑树Fig.3 Two CISTs of K(2k×n),k≥2,n≥3

(2)K((2k+1)×2t)的染色规则,这里k≥1,t≥2.

1)K((2k+1)×4),k≥1的染色规则：

a)染红色的边：

b)染蓝色的边：

c)不染色的边：

((0,0),(2k,3))以及((0,1),(2k,2)).

图4给出了按照上述方法所得的染色.

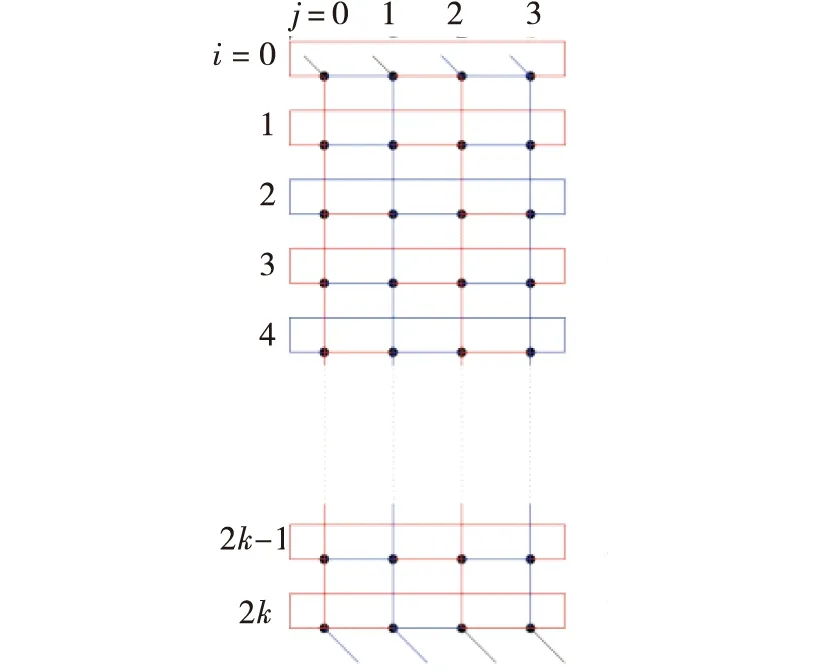
图4 K((2k+1)×4),k≥1的一组完全独立支撑树Fig.4 Two CISTs of K((2k+1)×4),k≥1

2)K((2k+1)×(4t+2))的染色规则, 这里k≥1,t≥1.

a)下列集合中的边染为红色：

b)下列集合中的边染为蓝色：

c)不染色的边有两条, 分别为((0,0),(2k,4t+1))以及((0,2t),(2k,2t+1)).

按照该染色方法我们得到图5.

3)K((2k+1)×4t)的染色规则,k≥1,t≥2.

a)下列集合中的边染为红色：

b)下列集合中的边染为蓝色：

c)不染色的边有两条, 分别为：((0,0),(2k,4t-1))和((0,2t),(2k,2t-1)).

实际上，K((2k+1)×4t)的染色方案可从图5所示的K((2k+1)×(4t+2))染色方案得到：图5所示的j列，其中j=2t-2,2t-1,…,2t+3,被图6所示的4列取代.后面的列按照顺序重新标号即可.

图5 K((2k+1)×(4t+2)),k≥1的一组完全独立支撑树Fig.5 Two CISTs of K((2k+1)×(4t+2)),k≥1,t≥1

图6 替换结构Fig.6 Replacement structure

(3)K((2k+1)×(2t+1))的染色规则,这里k≥1,t≥1.

1)K((2k+1)×3),k≥1的染色规则:

a)下列集合中的边染为红色：

∪j=0.2((0,j),(1,j))

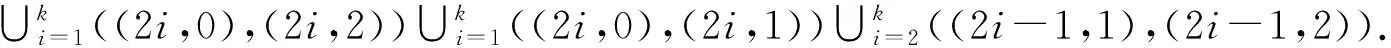
b)下列集合中的边染为蓝色：

((0,0),(2k,2))

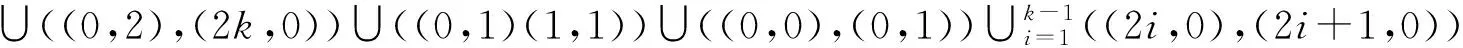
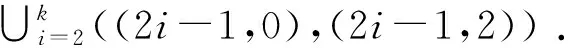
c)不染色的边有两条, 分别为((0,0),(0,2)) 和((1,1),(1,2)) .

图7给出了按照该染色方法所得图例.

图7 K((2k+1)×3),k≥1的一组完全独立支撑树Fig.7 Two CISTs of K((2k+1)×3),k≥1

2)K((2k+1)×(2t+1)) ,k≥1,t≥2,的染色规则：

a)下列集合中的边染为红色：

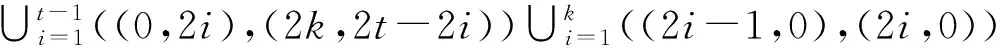
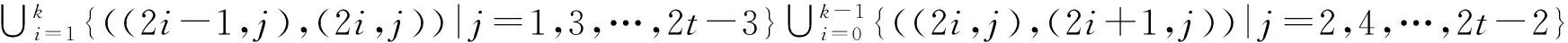
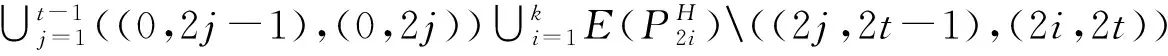
b)下列集合中的边染为蓝色：

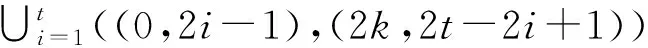
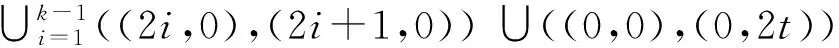
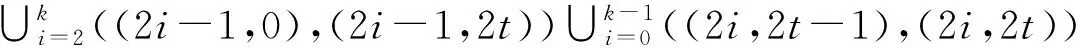
c)不染色的边有两条, 分别为((1,0),(1,2t)) 和((2k,0),(2k,2t)) .

图8给出了这种情形下的染色方案.

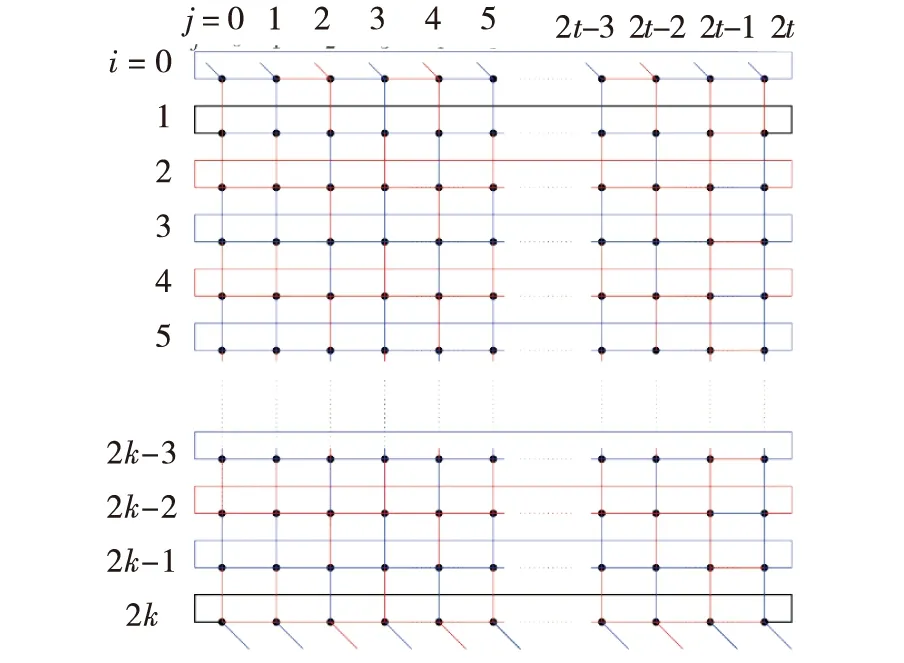
图8 K(2k+1)×(2t+1),k≥1,t≥2的一组完全独立支撑树Fig.8 Two CISTs of K(2k+1)×(2t+1),k≥1,t≥2

可以验证, 红(蓝)色边各导出K(m,n)的一棵生成树, 在每组染色过程中不被染色的边有两条.因为K(m,n)有2mn条边, 两棵支撑树占用了2mn-2条边, 所以还剩两条边不在两个完全独立支撑树中.下面我们证明不同颜色的边及所有点构成的两颗树是图的一组完全独立支撑树.

可以看出我们没有对边进行重复染色, 所以两个完全独立支撑树中没有重复的边.从图中可以看出，蓝色顶点在红色边导出的树中为叶子节点, 在蓝色边导出中为中间节点；红色顶点在蓝色边导出中为叶子节点，在红色边导出中为中间节点，即同一顶点只在蓝边图或红边图中的一个图度数大于1, 根据定理1.2，我们可以判断这两个支撑树是K(m,n)的一组完全独立支撑树.故定理得证.

3 结 论

显然K(m,n)的连通度与其参数有关，但是基于完全独立支撑树的角度, 可以确定它均存在两个完全独立支撑树，且最多只存在两个.通过对m和n的奇偶性进行分类，可以分为四大类，即奇×奇、奇×偶、偶×奇、偶×偶.实际操作中, 我们把偶×奇、偶×偶归为一类，找到了K(2k×n),k≥2,n≥3的一组完全独立支撑树.之后把奇×偶的情形又分为两个子类, 找到了K((2k+1)×(4t+2))和K((2k+1)×4t)，k≥1,t≥1的一组完全独立支撑树.最后找到了K((2k+1)×(2t+1)),k≥1,t≥1的一组完全独立支撑树.至此, 我们找到了K(m,n)一组完全独立支撑树.