砌体填充墙平面内损伤对平面外抗震性能的影响
2022-01-05马金铠孔璟常王晓敏赵伟通曲淑英
马金铠,孔璟常,王晓敏,赵伟通,曲淑英
(1.烟台大学 土木工程学院,山东烟台 264005;2.中国地震局工程力学研究所,黑龙江哈尔滨 150080)
0 引言
砌体填充墙是钢筋混凝土框架结构中最常用的隔墙和围护构件。由于平面布置灵活、施工简便、造价低廉等优势,填充墙钢筋混凝土框架结构被广泛应用[1]。目前,砌体结构抗震加固[2]也取得了很大的研究进展。填充墙作为脆性非结构构件与钢筋混凝土延性结构构件组成复杂的结构体系,现行的规范和结构设计对填充墙的考虑甚少。在地震作用下,填充墙受到平面内和平面外地震作用的共同作用,钢筋混凝土框架与填充墙也存在协同工作机制。汶川地震[3-5]、芦山地震[6-7]和长宁地震[8]震害显示,填充墙的存在增大了结构侧向刚度,产生了不理想的“强梁弱柱”等破坏模式。此外,填充墙平面外倒塌会对生命及财产安全造成极大威胁,并严重影响灾后救援和人口疏散等工作的开展。因此结构抗震设计和分析中单独考虑填充墙平面内或平面外的地震响应是不安全的[9],应充分考虑填充墙平面内外抗震性能的耦合机理。
当地震作用方向与结构主轴存在一定角度时,填充墙会同时受到平面内和平面外地震作用,填充墙平面外失效前就已经产生了平面内损伤,这种损伤多数是由钢筋混凝土框架的平面内侧移对墙体造成的挤压破坏。国内外学者设计了不同的试验对填充墙抗震性能进行了研究,如采用气囊加载方式对填充墙进行平面外加载测试[10-12]。Angel等[10]就填充墙钢筋混凝土框架结构平面内外耦合抗震性能进行了试验研究,结果表明填充墙经平面内损伤后平面外的承载力最高可降低50%,并分析了墙体拱机制的形成,首次提出了平面内损伤对平面外承载力折减之间的经验公式。Flanagan等[11]的试验结果表明填充墙平面内损伤对平面外刚度影响较大,平面内损伤较小时对平面外抗震性能影响不明显。也有学者通过四点加载方式对填充墙进行平面外加载测试[13-14],Ricci等[15]和Risi等[16]对填充墙钢筋混凝土框架结构进行了平面内外的组合加载试验,研究了经平面内损伤后填充墙平面外承载力的变化规律,基于试验结果,对比分析了已有研究[10,17-19]中的平面外承载力折减系数,提出了相应的拟合公式。Xie等[20]基于试验和一系列研究结果,提出了填充墙平面外承载力折减系数与平面内层间位移角和高厚比的经验公式。Agnihotri等[21]与Dolatshahi等[22]分别通过数值模拟和试验手段研究了这一损伤耦合效应。以上研究,均是将填充墙平面内卸载之后进行平面外加载,这种加载方式与震损填充墙在余震作用下平面外承受荷载的情况吻合。但是实际地震作用的方向与结构主轴之间存在一定的角度,即填充墙是同时承受平面内和平面外地震作用的,因此有必要研究平面内维持加载的情况下填充墙的平面外抗震性能。赵伟通[23]设置平面内维持加载和平面内卸载对照组,通过5榀填充墙的拟静力试验研究了平面内损伤对平面外抗震性能的影响。
由于试验研究周期长、造价高等原因,限制了对影响参数的系统研究,因此国内外学者通过数值模拟,对填充墙钢筋混凝土框架结构的抗震性能开展了一些研究。在有限元模拟中合理选用材料的本构有利于数值模拟的收敛性和准确性,Lematire[24]提出了混凝土损伤方程,Lubliner等[25]和Lee等[26]提出了混凝土损伤塑性理论及模型。方自虎等[27]、李伟琛等[28]和张劲等[29]对ABAQUS中混凝土损伤塑性模型(CDP模型)进行了大量的研究。Nasiri等[30]利用ABAQUS对填充墙钢筋混凝土框架进行分离式建模,研究多种参数对墙体平面外抗震性能的影响。高垚等[31]、张宇康等[32]、陈东方[33]等基于ABAQUS对不同类型填充墙进行了参数分析研究。Kong等[34-35]基于ABAQUS研究了平面内外加载次序对填充墙钢筋混凝土框架抗震性能的影响,结果表明填充墙的平面外损伤对其平面内性能具有较大的不利影响。综上所述,填充墙平面内外抗震性能的数值模拟研究取得了一定的进展,但是在平面内维持加载与卸载两种情况下,对填充墙平面外抗震性能还缺乏科学的认识。
本文基于已有试验[21],通过ABAQUS有限元分析软件对填充墙钢筋混凝土框架试验试件进行了分离式建模,利用试验数据验证了模型的可靠性。研究了平面内维持加载与卸载两种情况下,不同的平面内损伤对填充墙平面外抗震性能的影响。
1 试验简介
1.1 结构设计
本文选取文献[21]中的试验,试验中填充墙钢筋混凝土框架结构示意图和配筋图如图1、图2所示,其中地梁的尺寸为3500mm×500mm×400mm(长×宽×高)。填充墙的高度为1400mm,宽度为2100mm。框架柱的尺寸为200mm×200mm×1900mm(长×宽×高)。上方框架梁的尺寸为2700mm×150mm×300mm(长×宽×高)。

图1 框架尺寸及配筋(单位:mm)Fig.1 Dim ension and reinforcem ent in form ation of RC fram e(unit:mm)

图2 RC梁柱的断面尺寸及配筋(单位:mm)Fig.2 Section design of the RC beam and colum n(unit:mm)
1.2 材料属性
试验中选用蒸压加气混凝土砌块砌筑填充墙,砌块尺寸为290mm×100mm×90mm(长×宽×高),强度等级为A5;钢筋混凝土框架所选用的混凝土等级为C30;砂浆为M 5强度型号混合砂浆,砂浆厚度为10mm;钢筋混凝土框架中梁、柱纵筋选取HRB400,箍筋为HPB300。试验中混凝土、砌体、钢筋的力学性能见表1。
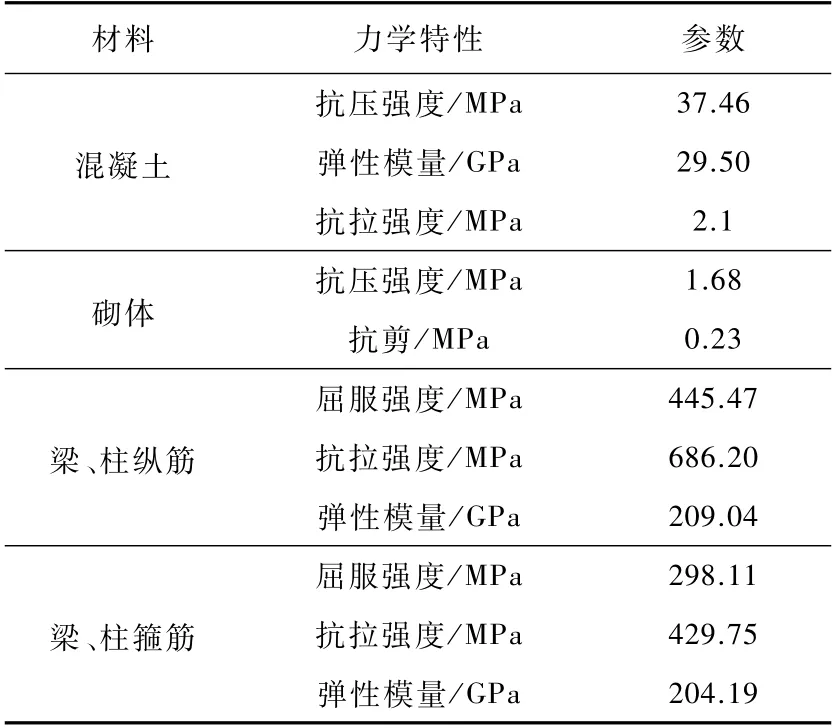
表1 材料实测力学性能Tab.1 M echanical p roper ties of m aterials
1.3 加载仪器布置
如图3所示,试验的加载仪器主要由三部分组成:竖向加载装置、平面内加载装置和平面外加载装置。首先将试件放置在设置有双排地锚孔的加载台架中,在试件的地梁处设置地锚连接孔,用高强螺栓将其与台架锚固,保证试件在各方向加载时,不会出现偏移。另外试验中设置了滚轴支护固定装置。对于竖向加载,在框架柱顶部设置分配梁,上部的压力机通过分配梁对框架柱施加均匀的竖向力,轴压比为0.4,竖向荷载的目标值取321.6kN。平面内加载装置由平内作动器、4个端板和4根高强螺杆用高强螺栓连接而成,其中平面内作动器固定在反力架上,以保证平面内加载有稳定的作用力,平面内加载至所设计的层间位移角值。试验中选取四分点集中加载方式来测试平面外承载力,平面外四点集中加载在墙体中的具体位置如图3所示。平面外加载装置由平面外作动器、四分点加载板组成。为了防止试件在平面外加载时框架梁产生平面外位移,设置了滚轴支护,支护上方设置的滚轴还可在平面内加载时,保证试件能够在平面内方向自由滑动。
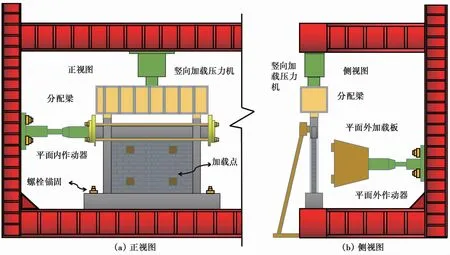
图3 试验加载装置Fig.3 Load ing setup in the test
2 基于ABAQUS的有限元模拟方法
2.1 钢筋混凝土框架的有限元模拟
在ABAQUS有限元模拟中,钢筋混凝土框架结构所用的钢筋均采用桁架单元(T3D2)进行模拟,钢筋的本构采用的为理想双折线弹塑性模型,受拉与受压曲线一致,本构关系式如式(1)所示:

式中,εy为钢筋屈服对应的应变。
框架中混凝土的单元类型为三维实体单元(C3D8R),材料属性为损伤塑性模型(CDP模型)。参考《混凝土结构设计规范GB50010-2010》[36],给出混凝土本构关系式定义受拉与受压的本构关系曲线。
单轴受压时混凝土的本构关系为:
当x≤1时,
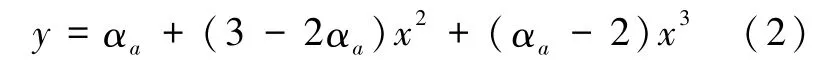
当x>1时,
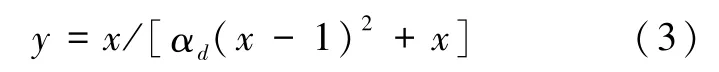
式中,x=ε/εc,y=σ/f*c;αa、αd为混凝土受压时曲线方程上升和下降段的参数;f*c为单轴混凝土抗压强度;εc为混凝土达到峰值应变。
单轴受拉时混凝土本构关系为:
当x≤1时,
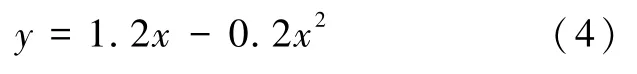
当x>1时,
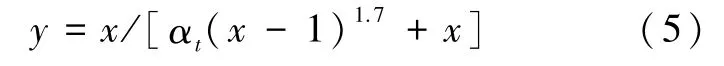
式中,x=ε/εt,y=σ/f*t;αt为混凝土受压时曲线方程上升和下降段的参数;f*t为单轴混凝土抗拉强度;εt为混凝土达到极限应力时的应变。
为了更好地模拟混凝土在平面内的受力特点,针对混凝土非线性性能,本文采用ABAQUS提供的混凝土塑性损伤模型(CDP模型)。在CDP模型中,通过定义和调试混凝土的黏性参数,模拟填充墙钢筋混凝土框架在平面内承载力的下降段。引用弹塑性损伤理论,定义混凝土的损伤因子和开裂应变,来模拟体现混凝土在拉伸和压缩时的变形和裂缝开展。本文定义混凝土塑性损伤模型中的塑性参数及压缩和拉伸损伤因子等,见表2和表3。

表2 塑性参数Tab.2 Plasticity param eters
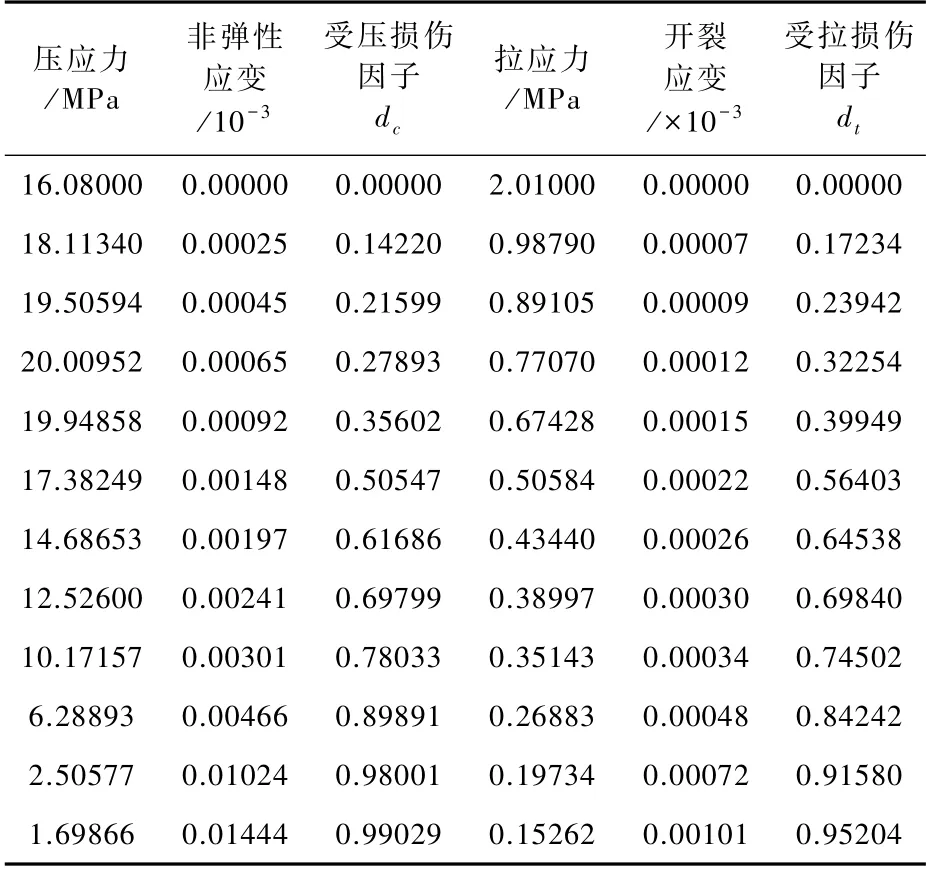
表3 混凝土材料特性Tab.3 M aterial p roperty of the concrete
ABAQUS中的Tie连接可实现各部件之间的永久捆绑,该连接方式利用“主-从公式”定义表面约束,防止主接触面与从面之间的相对滑动。本文中将梁柱混凝土分别进行独立建模,然后采用Tie连接组装,形成混凝土框架结构。钢筋与混凝土之间采用Embedded连接,与Tie连接相比,该连接方式的自由度较大,可以在多个部件相互干涉的情况下建立连接,体现钢筋内置在混凝土中的力学性能。
2.2 砌体填充墙以及墙框界面的有限元模拟
为了更好地模拟填充墙沿砂浆层的开裂滑移,本文对填充墙采取分离式建模的方法,如图4所示。分离式建模方法是,将砌块周围砂浆层厚度的一半与砌块看作整体,形成组合砌块。组合砌块采用实体单元(C3D8R)模拟,组合砌体的材料属性采用损伤塑性模型。对于分离式建模下的组合砌块应力-应变关系的选取,采取的是文献[10]中Angel所提出的砌体本构公式进行定义:
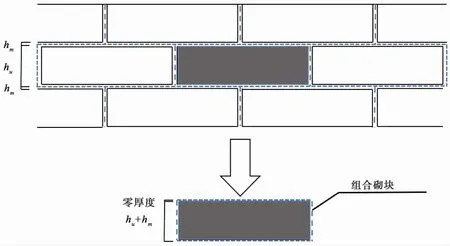
图4 分离式建模Fig.4 Separated m odelling

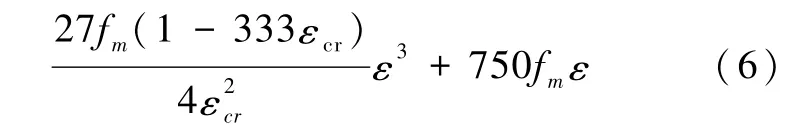
式中,εcr为砌体的压溃应变;fm为砌体的抗压强度。刘桂秋[37]基于大量的试验研究确定了压溃应变与峰值压应变(εmax)的关系,关系式为εcr=1.6εmax,本文取εmax=0.003。
在ABAQUS的相互作用模块下,通过在相邻的组合砌块之间建立接触对来模拟砂浆层,设置表面-表面接触内聚相互作用,在相互作用属性中设置四类接触属性:砌块之间的接触、墙体与地梁之间的接触、墙体与框架柱之间的接触、墙体与框架梁之间的接触,如图5所示。通过定义接触对的黏性接触行为、摩擦行为和硬接触属性来模拟砂浆层的力学性能。在填充墙受力初期,黏性接触行为发挥效果,通过定义Knn、Kss、Ktt3个黏性刚度来抵抗外部拉力和剪切力,当超过弹性范围后,接触面强度发生损伤,接触刚度开始退化,接触面间定义的摩擦行为开始发挥作用,黏性行为完全损伤后退出工作,仅由摩擦力抵抗界面切向力,硬接触抵抗界面压力。切向行为中“罚”摩擦通过摩擦系数联系摩擦力和界面正应力,本文摩擦系数取0.7。填充墙和框架之间的砂浆层同样采用接触对进行模拟。通过定义墙框界面的接触对属性来模拟墙框之间的开裂滑移。
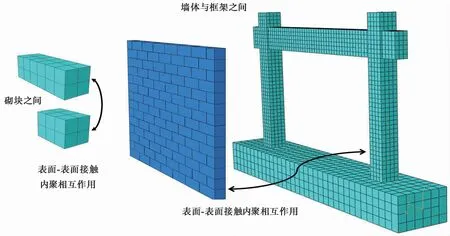
图5 填充墙RC框架接触示意Fig.5 Con tact schem atic diagram of the in filled RC fram e
2.3 荷载及边界条件的设置
2.3.1 荷载
正确选取材料的本构关系和准确设置模型的受力情况,对有限元模拟的准确性起到重要的作用。根据填充墙钢筋混凝土框架结构在试验中的实际受力与加载顺序情况,按照顺序分别设置重力荷载、竖向荷载、平面内水平荷载和平面外水平荷载等4个分析步。其中,重力荷载及竖向荷载在后续的分析步中均处于持荷状态,平面内水平荷载则视情况在后续的平面外加载分析步中设置持荷或卸荷状态。
(1)重力荷载:对整个模型设置重力荷载,沿竖向坐标轴的负方向设置重力加速度9.8m/s2。
(2)竖向荷载:轴压比取0.4,竖向荷载的加载值取321.6kN。在有限元模型中可在框架柱的上表面设置施加压强来模拟竖向力的加载,压强取8.04MPa。
(3)平面内水平荷载:在设置平面内加载前,首先进行耦合约束。在框架梁的左端设置平面内的参考点RP,将RP点与框架梁端表面设置耦合相互作用,使整个框架随RP点的变化而变化。用位移加载控制平面内的变化,取1%层间位移角(17mm)作为平面内的位移控制加载。其中面内0.5%、1%、2%层间位移角对应分析步时长分别为0.5s、1s和2s。
(4)平面外水平荷载:在设置平面外加载前,首先设置平面外四分点加载面,其次在填充墙模型中设置平面外的RP点,将平面外RP点与四分点加载面进行平面外方向的耦合约束。平面外用位移加载进行控制,平面外控制加载的位移取0.05m。
2.3.2 边界条件
根据填充墙钢筋混凝土框架在试验中的固定与支护方式。首先将模型中的地梁沿底面进行固结,防止整个模型在平面内外加载时沿平面内和平面外方向滑移;其次将框架梁和框架柱沿平面外方向进行位移为0的设置,防止框架梁与框架柱在平面外加载时沿平面外方向移动,以免对平面外的承载力造成误差。在ABAQUS中模型约束、荷载、边界条件设置及网格划分如图6所示。

图6 模型约束、荷载、边界条件设置及网格划分Fig.6 Constrain ts,loads,boundary conditions and m esh of m odels
3 有限元模型可靠性验证
3.1 平面内模拟验证
由于试验中试件在平面内只加载到1%层间位移角(17mm),而本文中有限元模拟需要加载到2%层间位移角(34mm)。所以在模拟填充墙钢筋混凝土框架平面内承载力时,需加载到2%层间位移角,取前面1%层间位移角的位移-荷载曲线进行验证。
在混凝土材料定义的CDP模型中,损伤因子dc和拉压刚度恢复参数(ωt、ωc)共同决定平面内位移-荷载曲线的趋势,尤其是ωt、ωc对平面内下降段出现的先后起到决定性的作用。当ωc=1时,表示混凝土受压时弹性模量的斜率无变化,表现出无损伤状态;当ωc=0时,表示混凝土受压时,损伤过大不能恢复。同理,受拉刚度恢复系数ωt=1和ωt=0同前文所述。本文通过取ωc=0.4,ωt=0.4;ωc=0.5,ωt=0.5;ωc=0.6,ωt=0.6这3组参数进行对比试算,得到平面内的位移承载力曲线如图7所示。取每一组参数所得的曲线与试验数据进行对比,得到当ωc=0.4,ωt=0.4时,模拟所得平面内位移-荷载曲线与试验曲线吻合度较大,如图8所示。为体现平面内加载的破坏状况,图9给出平面内有限元模拟所得裂缝图,可以看出填充墙在平面内侧向水平荷载作用下主要表现为对角传力机制。
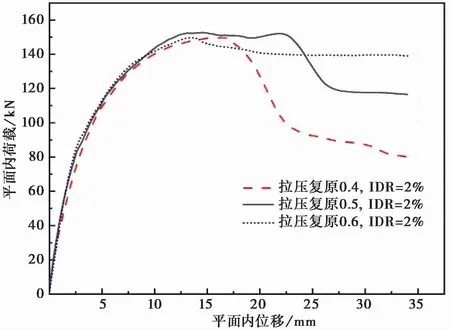
图7 各拉压刚度恢复系数对比Fig.7 Com parison of tension and com p ression stiffness recovery coefficients

图8 模拟所得平面内荷载-位移曲线与试验对比Fig.8 Com parison of in-p lane load-disp lacem ent curves in the sim u lation and experim ent
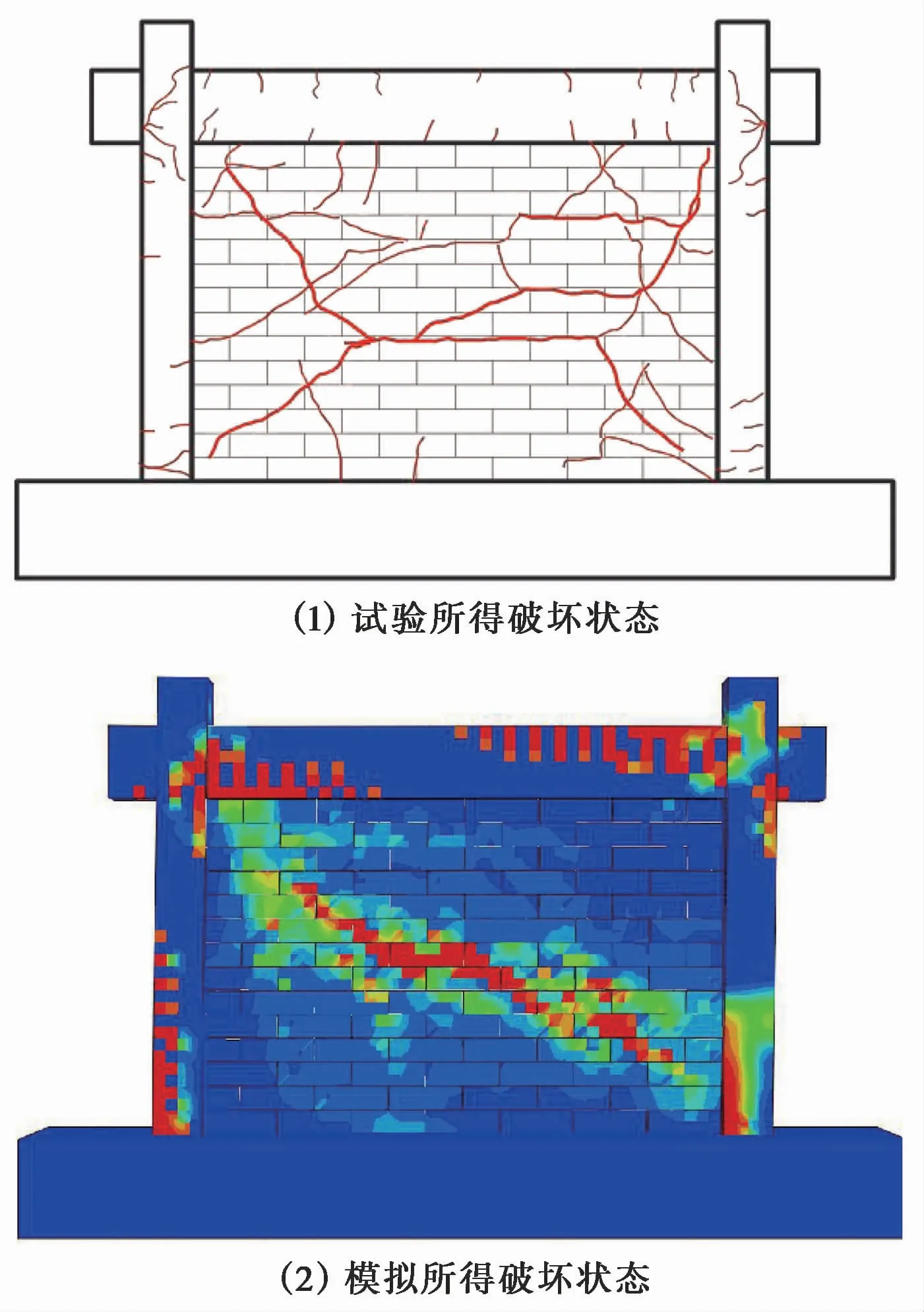
图9 平面内试验所得破坏状态与模拟结果的对比Fig.9 Com parison of dam age states obtained from the in-p lane test and the sim u lation
3.2 平面外模拟验证
取试验中纯平面外加载的试件(W-OOP模型)、保持平面内层间位移角(IDR=1%)进行平面外加载的试件(W-ML2模型)、平面内IDR=1%卸载后进行平面外加载的试件(WUL2模型)等3个试件进行有限元模拟,将模拟所得平面外位移-荷载曲线与试验曲线进行对比验证。图10~图12分别给出了试验与模拟的位移-荷载曲线对比,可以看出有限元模拟所得峰值荷载之前的整体趋势与试验吻合较好,试验所得荷载在峰值后急剧下降,表现出很强的脆性。为进一步与试验的破坏状态进行对比,选用ABAQUS/History Output Manager中的DAMAGEC变量来模拟填充墙破坏的状况。图13~图15中给出了各模型的损伤破坏云图,试验所得裂缝图与有限元模拟所得裂缝图的对比,可以看出有限元模型能够较好地模拟出填充墙平面外开裂状况和裂缝分布情况。

图10 W-OOP模拟结果与试验对比Fig.10 Com parison of disp lacem en t-load cu rves obtained from the out-of-p lane loaded specim en(W-OOP m odel)sim u lation and the test

图11 W-M L 2模拟结果与试验对比Fig.11 Com parison of disp lacem en t-load cu rves obtained from the out-of-p lane loaded specim en(W-M L2 m odel)sim ulation and the test
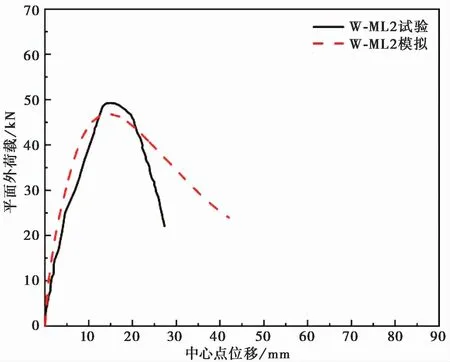
图12 W-UL2模拟与试验对比Fig.12 Com parison of disp lacem en t-load cu rves obtained from the out-of-p lane loaded specim en(W-UL 2 m odel)sim u lation and the test
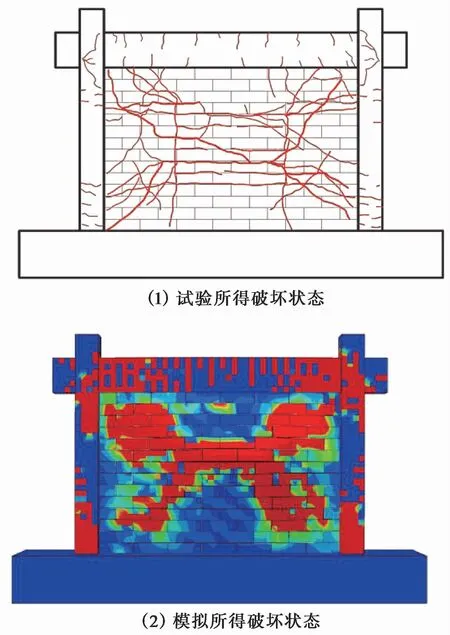
图15 卸载试验所得破坏状态与模拟结果的对比Fig.15 Com parison of dam age states ob tained from the un load ing test and the sim u lation
3.3 平面内外模拟可靠性分析
根据上文模拟结果,为充分验证模型的可靠性,从初始刚度、峰值割线刚度和峰值荷载3个方面对W-OOP、W-ML2及W-UL2 3个试件的模拟与试验结果进行误差分析,从而验证模型的可靠性,为分析其余工况的模拟数值提供可靠的依据。其中平面内外初始刚度取填充墙位移-荷载曲线峰值荷载的20%对应的割线刚度为初始刚度,具体分析数据见表4。
从表4分析得误差数据可知:
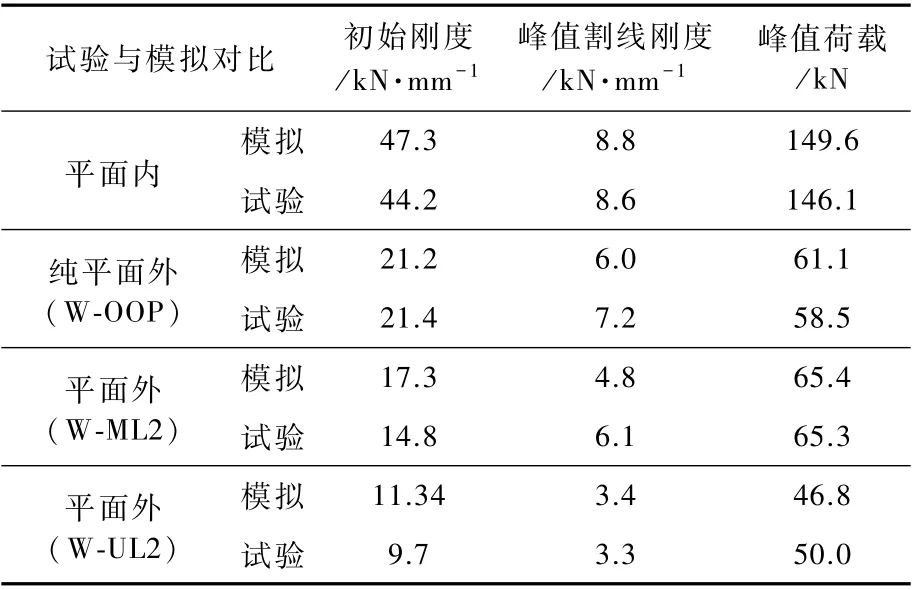
表4 有限元模拟所得各试件平面内外刚度与承载力与试验结果的对比Tab.4 Com parison of the in-p lane and out-of-p lane stiffness and bearing capacity of each specim en obtained from the finite elem ent sim u lation abd the test
(1)对于平面内模拟,试件在平面内1%层间位移角时,试验中峰值荷载为146.1kN,有限元模拟对应荷载为149kN,模拟平面内初始刚度与试验结果的误差为7.00%,峰值荷载的误差为2.40%,模拟结果与试验结果基本一致,位移-荷载曲线也基本吻合。
(2)对于纯平面外模拟,试验所得峰值荷载为 58.5kN,有限元模拟所得峰值荷载为61.1kN,峰值荷载和初始刚度的误差分别为4.40%和0.90%,模拟结果与试验结果较为吻合。对于纯平面外位移-荷载曲线的下降段,试验和有限元模拟有明显差别。这是因为在试验中墙体达到峰值荷载后,砂浆层断裂破坏严重,墙体拱机制骤然失效而丧失承载力,所以平面外位移-荷载曲线呈现出急剧下降的趋势。而有限元模型中砂浆断裂破坏存在一定的过程,所以曲线下降段较为平缓。
(3)对于试件W-ML2,试验所得平面外峰值荷载为 65.3kN,有限元模拟对应荷载为65.4kN,误差为0.15%,与试验吻合较好。平面外初始刚度有一定误差,因为在试验中平面内加载到1%层间位移角时,部分砌块和砂浆层断裂破坏,使平面外刚度下降较多。而有限元数值模拟的约束条件较为理想,维持平面内层间位移角对墙体形成挤压,加强了墙体的边界条件,且有限元模型无法模拟砌块的断裂,故有限元模型的初始刚度虽然小于纯平面外模型的初始刚度,但大于试验所得初始刚度。试验所得曲线下降段较为陡峭,原因同纯平面外加载试件一致。
(4)对于试件W-UL2,模拟所得平面外峰值荷载及初始刚度误差分别为6.40%和30.34%。两者的峰值荷载差别较小,而在初始刚度方面模拟值要大于试验值。这是因为在试验中填充墙钢筋混凝土框架经历了平面内加卸载过程,部分砌块产生裂缝,填充墙的整体性减弱。而有限元模型无法模拟砌块的断裂,所以平面内卸载后填充墙的平面外初始刚度要大于试验值。
从以上的误差分析可以得出,W-OOP有限元模型、W-ML2有限元模型、W-UL2有限元模型与试验结果的对比基本吻合。由图13裂缝对比可以看出,无论是试验还是模拟,裂缝基本呈现出沿对角线发展的分布,出现拱形承力机制,在破坏模式上与试验相吻合,证明了有限元模型的可靠性。
4 填充墙平面内损伤对平面外抗震性能的影响
为研究填充墙平面内损伤对平面外抗震性能的影响,如表5所示,本文设置两种加载方式:(1)对平面内维持加载的试件进行平面外加载,本文标记为W-ML1、W-ML2和W-ML3(W-ML系列试件),分别对应平面内加载至0.5%、1%、2%层间位移角,简化地研究作用不同平面内层间位移角的填充墙的平面外抗震性能;(2)将平面内卸载的试件进行平面外加载,本文标记为WUL1、W-UL2和W-UL3(W-UL系列试件),分别对应平面内加载至0.5%、1%、2%层间位移角,简化地研究不同震损填充墙在余震作用下的平面外抗震性能。
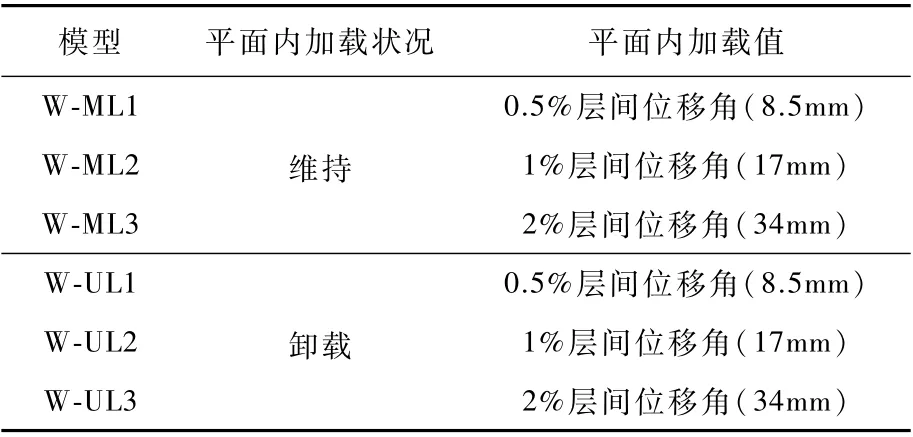
表5 模型工况Tab.5 Loading p rogram of analyticalm odels
对其余不同工况下的模型W-ML1、W-ML3、W-UL1、W-UL3进行模拟分析。各试件平面外的位移-荷载曲线,如图16和图17所示,可以看出在平面内维持加载和卸载两种工况下,平面外体现出不同的力学特性。图18给出了W-ML系列试件的平面内荷载-位移曲线,其中的直线下降部分表示填充墙在平面外加载过程中,平面内承载力的变化。由图18可以看出,在平面外加载过程中的各模型的平面内承载力出现了不同程度的下降,这是因为填充墙的平面外变形减弱了填充墙的平面内传力机制,从而使整个结构的承载力降低。图19给出了W-UL系列试件的平面内荷载-位移曲线,可以看出各试件的平面内荷载卸载为零后均出现了不同程度的残余位移。
4.1 平面内损伤对平面外初始刚度和承载力的影响分析
根据图16和图17的模拟结果,图20和图21给出了以纯平面外加载所得的峰值荷载和初始刚度为基准,各试件的平面外承载力与初始刚度的变化。从图中可看出,W-ML系列试件的平面外承载力随平面内层间位移角的增大呈现先增大后减小的变化趋势,且平面内维持在1%层间位移角时承载力达到最大,而初始刚度呈逐渐减小的变化趋势;墙体随着平面内加载的层间位移角增大,W-UL系列试件的平面外承载力和初始刚度均呈现逐渐减小的变化趋势。因每个模型的损伤及受力状态不同,所以对平面外抗震性影响也有所不同,对6个模型逐一进行分析。
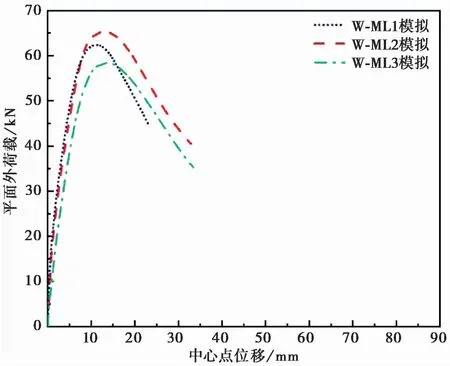
图16 W-M L系列试件平面外位移-荷载曲线Fig.16 Com parison of disp lacem ent-load curves ob tained from the out-of-p lane loaded specim en(W-OOP m odel series)sim u lation and the test
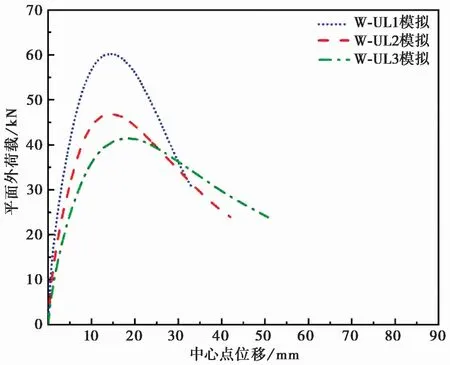
图17 W-UL系列试件平面外位移-荷载曲线Fig.17 Com parison of disp lacem en t-load cu rves obtained from the out-of-p lane loaded specim en(W-UL m odel series)sim u lation and the test
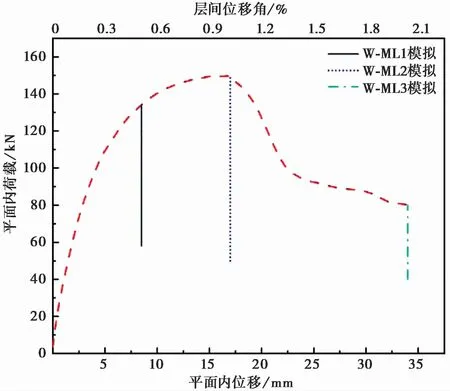
图18 W-M L系列试件平面内位移-荷载曲线Fig.18 Com parison of disp lacem en t-load cu rves obtained from the out-of-p lane loaded specim en(W-M L m odel series)sim ulation and the test
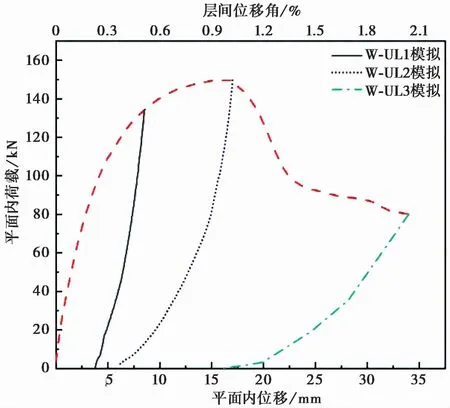
图19 W-UL系列试件平面内位移-荷载曲线Fig.19 Com parison of disp lacem ent-load curves obtained from the ou t-of-p lane loaded specim en(W-OOP m odel series)sim u lation and the test
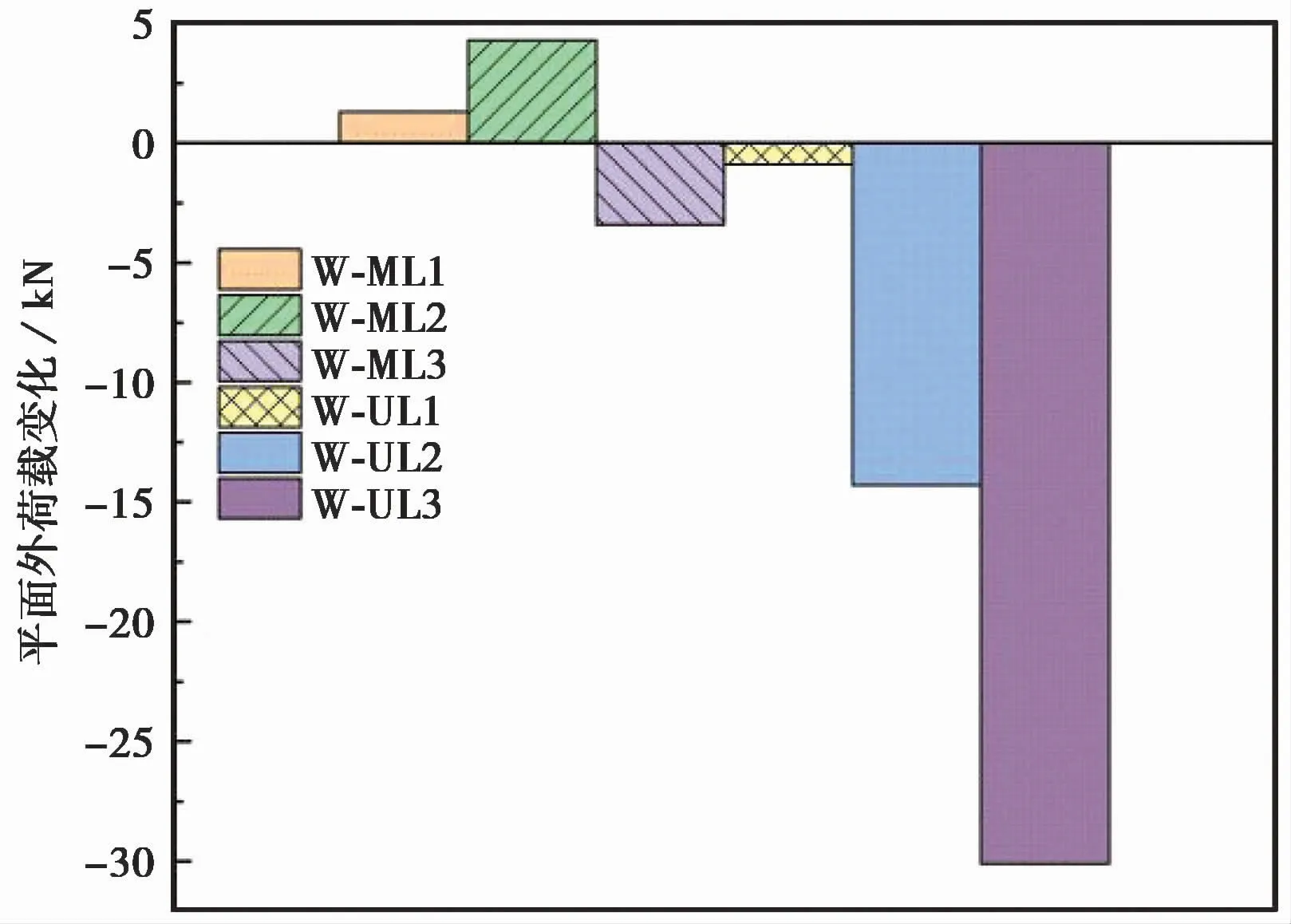
图20 平面外峰值荷载变化Fig.20 Variation of peak load of different W-M L m odel series under out-of-p lane loaded
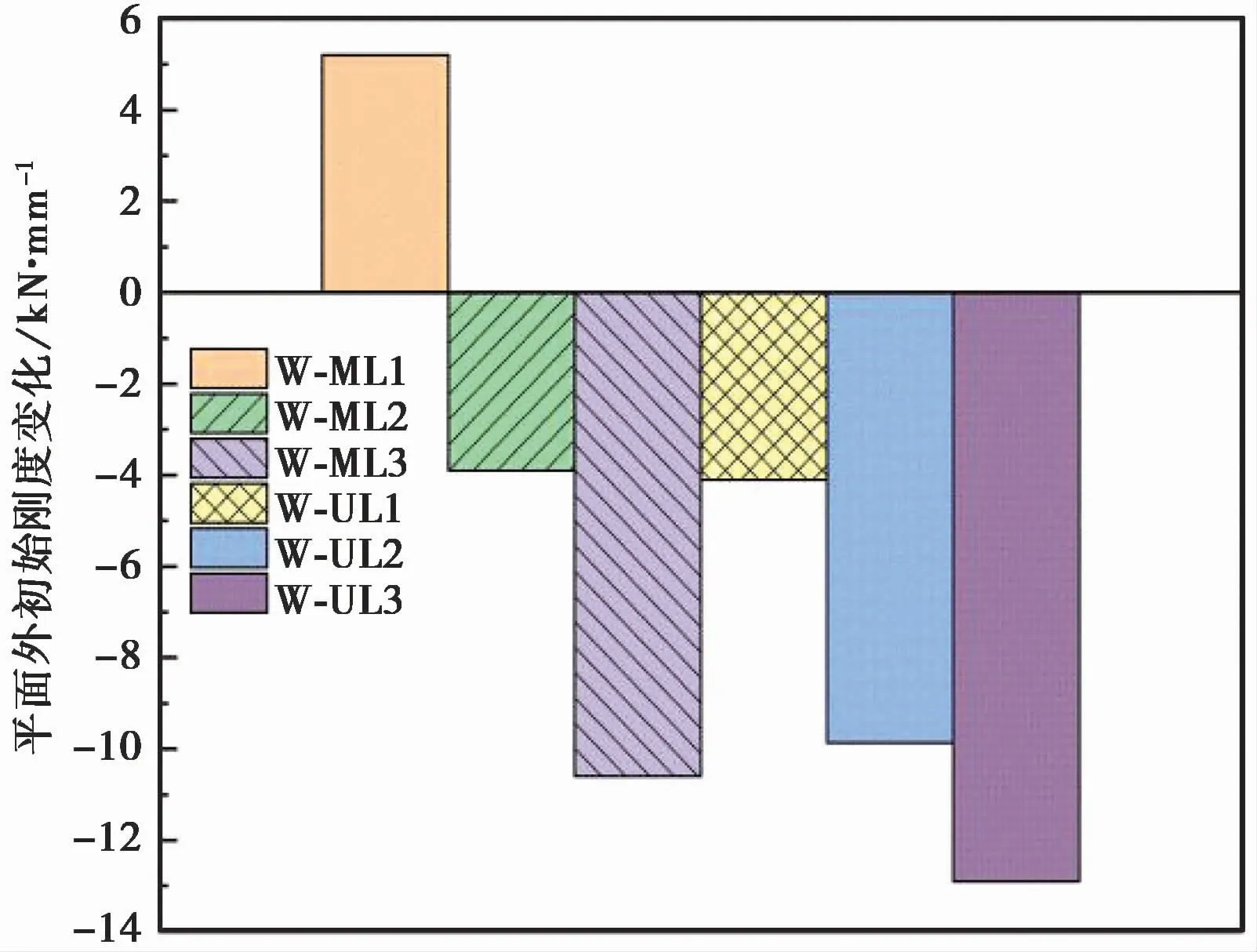
图21 平面外初始刚度变化Fig.21 Variation of initial stiffness of different W-M L m odel series under out-of-p lane loaded
(1)试件W-ML1的峰值荷载为62.3kN,初始刚度为26.4kN/mm,与W-OOP模型相比,分别提高了1.3kN、5.2kN/mm。这是由于平面内加载到0.5%层间位移角处在位移荷载曲线的上升段,如图18所示。维持结构的平面内层间位移角,使墙体在平面内受到挤压,墙体的边界约束条件得到了加强,所以试件W-ML1的平面外初始刚度和承载力均得到了不同程度的加强。
(2)试件W-ML2的峰值荷载为65.4kN,初始刚度为17.3kN/mm,与W-OOP试件相比,分别提高了4.3kN、降低了3.9kN/mm。如图18所示平面内在加载到1%层间位移角时,平面内荷载几乎达到结构承载力,试验中填充墙部分砂浆层断裂破坏,有限元模型则体现为砂浆层黏性接触行为超过了弹性范围,接触刚度开始退化,导致平面外刚度降低。因平面内维持在1%层间位移角,墙体受到两侧框架柱的约束和挤压,墙体的边界条件得到进一步加强,因此平面外承载力达到了所有工况中的最大值。
(3)试件W-ML3的峰值荷载为58.4kN,初始刚度为10.6kN/mm,与W-OOP试件相比,分别降低了3.4kN、10.6kN/mm。由于平面内加载到2%层间位移角时,试件处于平面内位移-荷载曲线的下降段,墙体破坏严重。在有限元模型中大多数砂浆层黏性接触面已经超过了弹性范围,接触刚度退化严重,导致平面外初始刚度下降较大。但由于平面内维持2%层间位移角时,墙体依然存在较强边界挤压条件,墙体变形受到约束。所以填充墙平面外承载力有所下降,但下降幅度并不大。
(4)试件W-UL1为平面内荷载卸载为0后进行平面外加载的工况,从图20和图21可看出,W-UL系列试件的平面外初始刚度和承载力均产生了不同程度的下降。其中W-UL-1试件的峰值荷载为60.1kN、初始刚度为17.1kN/mm,与 W-OOP 试件相比,分别降低了 0.9kN、4.1kN/mm。由于试件W-UL-1加载到0.5%平面内层间位移角,墙体产生一定的损伤。有限元模型中少数砂浆层黏性接触行为超过了弹性范围,接触面发生一定损伤,导致承载力和初始刚度均产生小幅度下降。
(5)试件W-UL2的峰值荷载为46.7kN,初始刚度为11.34kN/mm,与W-OOP试件相比,分别降低了14.3kN、9.86kN/mm。1%平面内层间位移角使填充墙产生了比较严重的破坏。在试验中,墙体内部砂浆层以及墙体与框架之间的砂浆层多数被破坏,在有限元模型中则体现为砌块之间的接触面以及墙体与框架的黏结接触多数被消耗,平面外承载力和初始刚度都有一定幅度的下降。
(6)试件W-UL3的承载力和初始刚度是最低的,与W-OOP试件相比,分别降低了50.73%、61.13%。平面内加载到2%层间位移角时,墙体破坏严重,主要体现为砂浆层的开裂和滑移破坏以及砌块的拉压损伤,平面内卸载后填充墙失去了框架柱的挤压约束,墙体整体性降低,边界约束条件减弱,使得填充墙平面外承载力和初始刚度的大幅度下降。
4.2 破坏模式分析
图22给出了6种工况下的破坏模式,其中图(a)~(c)为W-ML系列试件平面内外破坏模式。总体来看,由于填充墙在平面内维持作用下会改变平面外的受力方向,会使填充墙左下部分裂缝发展。试件W-ML1由于平面内加载幅度较小,框架损伤相对较小,在平面内维持加载的作用下,其平面外破坏模式与W-OOP的拱形破坏模式相似。试件W-ML2由于加载至1%层间位移角,框架损伤相对严重,主要体现在框架的梁柱的节点处的破坏。且在面内维持加载的作用下,使得填充墙面外受力不均,平面外的破坏模式主要沿平面内的斜裂缝处发展扩张,填充墙左下部分裂缝在面内维持作用下发展相对减弱。试件W-ML3无论是框架还是墙体破坏都最为严重,图22中可以看出,面外的损伤面积增大,填充墙左下部分裂缝依旧在在面内维持作用下发展相对减弱。
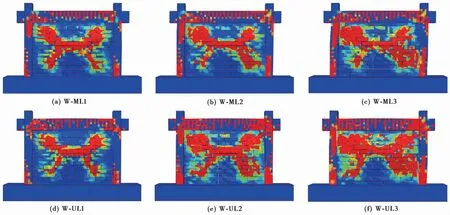
图22 试件平面内外破坏模式Fig.22 In-p lane and out-of-p lane dam agem ode of specim ens under six working conditions
图22中(d)~(f)为W-UL系列试件平面内外破坏模式。由图中可以看出,由于W-UL系列试件为填充墙平面内卸载后平面外的受力状况,面内损伤对面外的损伤程度影响较大,且随平面内层间位移角的增大,面外的损伤逐渐增加。这是因为填充墙在经历平面内损伤后,填充墙损伤严重,平面内卸载后墙体边界条件减弱,造成平面外方向的损伤严重。填充墙在平面内卸载后,平面内方向会产生残余位移。随着平面内层间位移角增大,平面内卸载后所产生的残余位移也随之增大,这会造成平面外不均匀的拱形机制破坏。
由以上破坏模式分析可以得出,不同加载条件下的平面内损伤对平面外破坏模式的影响是不同的。在平面内维持加载的条件下,由于平面内的维持,造成平面外方向的受力不均匀,所以对填充墙造成不均匀的拱形破坏。而在平面内卸载的条件下,由于平面内会产生残余位移,也对填充墙造成不均匀的拱形破坏。相对平面内维持加载而言,在平面内卸载条件下,对平面外损伤影响较为严重。并且随平面内随层间位移角的增大,平面外损伤越严重。
5 结论
本文基于ABAQUS对填充墙钢筋混凝土框架结构进行分离式建模,利用试验数据对数值模型进行验证和标定。以验证后的模型为参考,分别对应地震作用下同时承受平面内外荷载的填充墙平面外行为和震损填充墙在余震作用下的平面外行为,研究了平面内维持加载和卸载两种不同工况下,不同平面内损伤对填充墙平面外抗震性能的影响。主要得出以下结论:
(1)在平面内维持加载时,平面内损伤对墙体平面外承载力的影响较小,因为平面内IDR使填充墙的边界约束条件得到了加强,本文建议可以忽略对平面外承载力的影响。但平面外变形导致填充墙在平面内方向退出工作,其影响不容忽视。
(2)在平面内卸载时,平面内损伤对墙体平面外抗震性能的影响较大,且影响程度与砌块种类有关。对于本文采用实体蒸压加气混凝土砌块的填充墙,在平面内层间位移角为2%时,平面外承载力和初始刚度的下降幅度均超过50%。
(3)平面内维持加载和卸载都会对填充墙平面外造成不均匀的破坏模式。填充墙在平面内卸载的加载条件下,对平面外破坏模式影响较为严重,并且随平面内层间位移角的增大,平面外损伤越严重。
无论是平面内维持加载还是卸载,填充墙平面内损伤都会不同程度地影响平面外抗震性能,另外填充墙的平面外变形也会导致填充墙在平面内退出工作,在多层多跨整体结构中将导致潜在的薄弱层破坏。因此,在地震作用下单纯考虑填充墙平面内或平面外抗震性能均是不合理的,且应采取有效措施防止填充墙平面外变形过大或倒塌。由于本文所选取的试验以及有限元模型均为先平面内加载后平面外加载,然而这种拟静力加载方式并不能充分体现填充墙钢筋混凝土框架在地震作用下的真实受力机理。未来研究重点应放在适用于完好填充墙和震损填充墙同时承受平面内外地震作用的有限元模型。
