车辆稳定性控制系统LQR算法设计

龙文，刘豪

车辆稳定性控制系统LQR算法设计

龙文1，刘豪2

（1.东风柳州汽车有限公司乘用车技术中心，广西 柳州 545005；2.重庆理工大学，重庆 400054）

车辆稳定性控制系统能够有效提高车辆在极限工况下的性能，其主动横摆力矩施加算法是系统控制的核心。文章以车辆二自由度模型为基础，使用车辆响应偏差线性模型，设计了车辆稳定性LQR（Linear Quadratic Regulator）控制算法，获得了主动横摆力矩反馈矩阵；进行了车轮制动力施加决策和计算模块设计，得到了车辆控制的输入量；建立了Carsim和MATLAB联合仿真环境，进行了换道操纵、正弦操纵等开环操纵试验和双移线闭环试验。结果表明：车辆的横摆角速度能够有效跟踪参考模型值，质心侧偏角保持在稳定区域内。文章设计的控制算法能在一定程度上提高车辆的稳定性操纵区域，具有一定的应用价值。

车辆稳定性；线性二次型调节器；横摆角速度；质心侧偏角

引言

车辆在极端工况下容易失去稳定性，引起安全问题。提高该类工况下车辆稳定性的方式包括差动制动和主动转向等，但主动转向方式在车辆处于极限工况时的效果不明显，差动制动方式是该类工况下比较有效的方式[1]。差动制动横摆力矩施加算法是车辆稳定性控制系统的控制算法的核心内容，在文献[2]中，采用车辆二自由度模型作为参考模型进行模糊算法设计，该类方法避免了复杂的系统建模和分析过程，但是调整模糊会过分依赖经验和试验。在文献[3]中建立了包含方向盘转角输入和主动横摆力矩输入的系统模型，采用最优控制的方法设计了横摆力矩计算方法，该方法从机理上分析特性，但将方向盘转角作为干扰量设计系统，违背了车辆操纵的实际情况。

在车辆稳定性控制中，参考目标的选择非常重要，横摆角速度能够通过传感器测得，以该变量作为控制变量设计控制系统实现比较容易。但质心侧偏角是车辆稳定与否的重要表征[4]，特别是在稳定性控制发挥作用的极限工况区域，质心侧偏角参与控制变得更加重要。在文献[5]中，采用质心侧偏角相图确定稳定性控制边界，并以此设计稳定性控制算法。但大多数的研究以车辆二自由度模型作为参考对象，同时采用两者，在尚未进入严重非线性区域时，横摆角速度控制起到主要作用，在进入非线性区域后，质心侧偏角起到主要作用[6]。在文献[7]中，比较了采用线性模型的稳态响应和动态响应作为参考的效果，指出两者差异明显。

在本文设计控制算法时，采用车辆二自由度模型作为参考模型，以其横摆角速度和质心侧偏角动态输出作为参考，并结合车辆在施加主动横摆力矩后的模型，计算响应偏差模型，进而设计LQR算法。

1 车辆稳定性控制基本原理

差动制动是在非线性区域内稳定车辆的有效方式，其基本原理是在车辆发生激转或滑出等情况时，通过对单侧车轮施加制动力，产生绕质心的附加横摆力矩，该横摆力矩能够将车辆重新拉回较为稳定的状态。

1.1 车辆稳定性控制策略

图1 车辆稳定性控制策略

稳定性控制器包含两部分，主动横摆力矩计算模块和车轮选择模块。主动横摆力矩控制器通过算法生成当前状态下需要的主动横摆力矩大小，然后由车轮选择模块根据车辆当前的状态包括方向盘转角和所需的主动横摆力矩的施加方向进一步确定施加制动力的车轮，通过制动将车辆重新稳定到驾驶员的实际期望目标。

1.2 车辆稳定性的判断

车辆稳定与否主要通过质心侧偏角表征，在以往的研究中发现，车辆的质心侧偏角超过4度时，车辆就进入了非线性范围，且有可能逐渐失稳。因此车辆控制的目标之一是将质心侧偏角控制到一个比较小的范围内，在质心侧偏角较小时，车辆不参与控制。

2 控制算法设计

2.1 主动横摆力矩生成算法设计

理想的车辆具有中性转向特性，其横摆角速度的计算公式为：

其中，为车辆的纵向速度，为车辆的轴距，为前轮转角。

车辆的滑出和激转状态可以通过比较车辆实际的横摆角速度和计算得到的横摆角速度进行判断。按照这种方法计算得到的−r值可以作为车辆操纵性的指标。但大多数车辆具有不足转向特性，影响高速状态时的车辆操纵性能，所以通常选择车辆二自由度模型为参考模型，其状态方程为：

式中，β为质心侧偏角目标值；为横摆角速度目标值；1为前轴轮胎侧偏刚度；2为后轴轮胎侧偏刚度；为整车质量；为车辆纵向速度；I为车辆的横摆转动惯量；为质心到前轴的距离；为后轴到质心的距离；为前轮转角。

与采用二自由度线性模型相比，使用稳态模型作为参考模型幅值相等，但线性模型的响应略有滞后。

在车辆存在稳定性问题时，通常车辆已经处于非线性运行区域，车辆的侧偏刚度等都已经发生了变化，为了简化问题，通常假设其依然保持原来的刚度，在车辆稳定性控制中，会施加主动横摆力矩，施加后的车辆响应方程为：

学生对该课程的认知度不高 针对机械电子工程本科生开设的机器人学课程，教学大纲要求学生熟悉机器人技术发展概况及其在生物生产、仿生机械、特种机器人等方面应用的具体案例，掌握基本构成、工作原理、动力学分析、传感控制系统等基本知识[4]。但在教学过程中发现，学生对该门课程的积极性不高，认为内容多、难度大，不易理解，特别是对运动学中矩阵的变换，运动学、动力学等理论的推导分析，产生消极态度，久而久之，导致失去学习的兴趣。

定义△为质心侧偏角参考值与实际响应之间的偏差，△为横摆角速度参考值与实际响应之间的偏差。其表达式为：

将（3）与（2）相减，可得车辆偏差响应模型：

该方程体现了主动横摆力矩对车辆响应与参考输入之间的偏差的作用过程。即：

则转化为标准形式的状态空间方程：

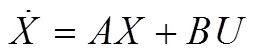
为了设计最优控制器，提出如下控制指标：

其中，矩阵用于使系统能够快速准确地将误差消除为零，R矩阵用于限制输入量不至于过大，超出车轮制动力提供的主动横摆力矩的能力。

LQR的最优控制输入量为：

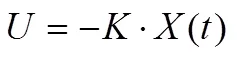
反馈系数矩阵可以直接根据系统的矩阵A，B，Q ，R直接获得。

2.2 主动横摆力矩的施加

在对车辆单侧的车轮施加制动力时，由于附着椭圆特性等的影响，制动力会引起侧向力的变化，最终导致附加横摆力矩的大小发生明显的变化。

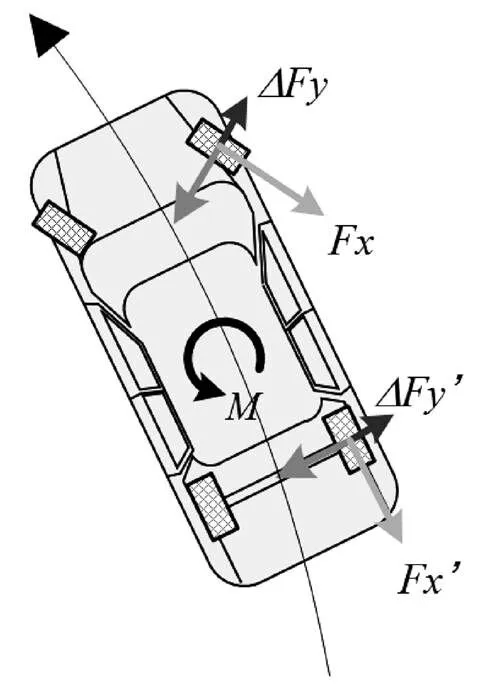
图2 同侧前后轮制动产生不同横摆力矩原理

在车辆的激转工况下（如图2所示），此时需对外侧车轮施加制动力以产生反方向的附加横摆力矩。如果对前轮施加，一方面制动力可以产生反方向的力矩，另一方面制动力的施加也减少了侧向力的提供，进一步增加了横摆力矩，因此在此种方式下，对前外轮的制动能够产生更加有效的结果。如果对后轮施加制动，虽然制动力产生的横摆力矩产生正向效果，但由制动力施加引起的侧向力的减小减弱了该效果，由此产生的叠加效果明显弱于前外轮。根据论文[8]的研究，具体制动力施加时的附加横摆力矩变化过程如图3所示：

图3 不同轮制动主动横摆力矩施加效果

因此，为了使计算得到的附加横摆力矩具有更好的效果，需判断方向盘转角、附加横摆力矩。具体如表1所示：

表1 制动施加车轮判断逻辑

方向盘转角附加横摆力矩车轮 δ＞0△M＞0左后轮 δ＞0△M＜0右前轮 δ＜0△M＞0左前轮 δ＜0△M＜0右后轮

3 控制仿真试验

3.1 联合仿真环境的建立

为了验证所设计的控制算法的效果，采用Carsim和MATLAB建立了联合仿真环境，该仿真环境具有驾驶员模型，能够通过模块调用直接进行开环和闭环操纵稳定性试验，建立的联合仿真环境如图4所示：

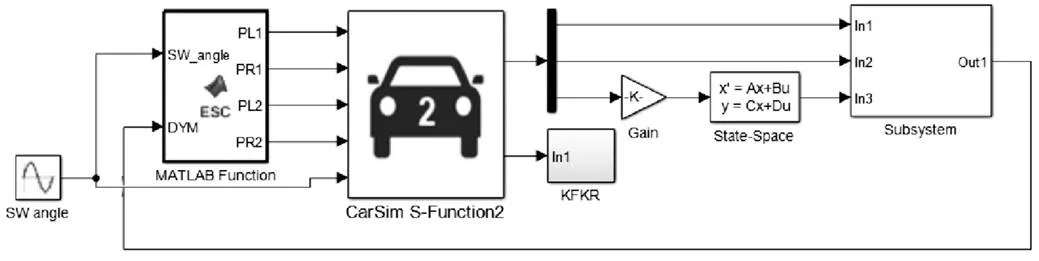
图4 CARSIM和MATLAB联合仿真环境

选用某D型车作为控制对象，其基本参数如表2所示：

表2 整车参数表

参数名参数值 整车质量/kg1 610 前轴到质心距离/m1.05 后轴到质心距离/m1.61 轮距/m1.565 横摆转动惯量/（kg/m2）2 398.4

3.2 试验设计

所进行的试验分为开环试验和闭环试验，开环试验用于对比在相同的方向盘转角输入下车辆在未控制和控制后的响应对比，以及控制过程中的输入。其中开环试验包含换道输入试验和正弦输入试验，闭环试验采用Carsim中建立的双移线试验工况进行检验。

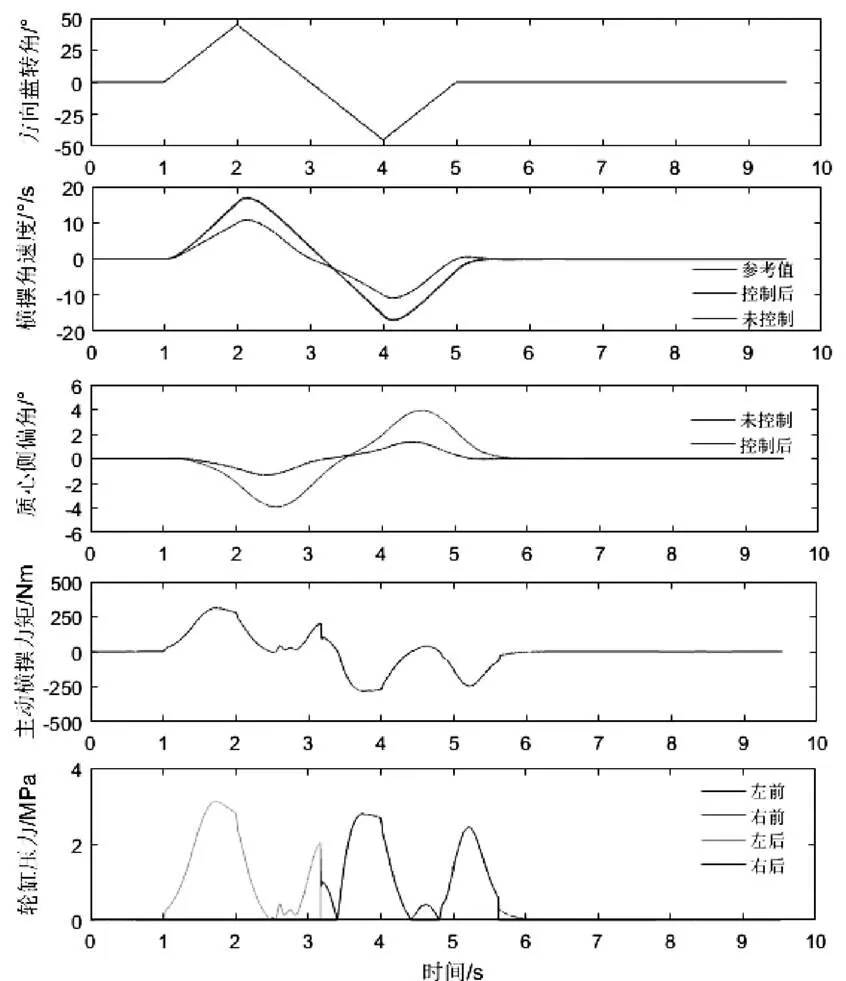
图5 换道试验结果

图5为换道输入试验的结果，其中车速设置为80 km/h，方向盘的转角输入最大值为45度，地面附着系数设置为0.5。在这种操纵下车辆的侧向加速度已经达到0.45，车辆已经进入非线性区域。

从图5可以看出，在车辆未经控制时，车辆的横摆角速度与理想的二自由度模型输出出现较大的偏差，车辆的质心侧偏角也达到了4度以上，这显示车辆已经进入了失稳状态。经控制后，横摆角速度的偏差消失，车辆响应遵从二自由度模型输出。同时质心侧偏角也较小，车辆的操纵总体符合驾驶员的期望。

图6为正弦输入试验结果，试验时车速为80 km/h，方向盘转角最大值设置为60度，输入整体较换道输入平缓，角频率为1 rad/s，路面附着设置为0.5。车辆整体的响应状态与换道输入趋势相同，在未经控制时，车辆的横摆角速度无法跟踪二自由度输出，质心侧偏角达到了20度，车辆已经呈现出比较大的失稳状态。经控制后，车辆的横摆角速度基本能跟随二自由度模型输出，质心侧偏角的最大值也在4度以内，基本保持了稳定。

图6 方向盘正弦操纵试验结果

图7为使用驾驶员模型的双移线闭环试验结果，该试验设置车速为80 km/h，地面附着为0.6。该类试验由于驾驶员在不同响应下的输入发生变化，所以无法直观对比横摆角速度和质心侧偏角响应，但可以对比车辆在稳定性控制系统开启和关闭状态下的输入。从图中可以看到，经控制后，车辆的方向盘转角输入较未控制时平缓，说明通过控制提高了寻迹性能后，车辆响应更容易达到驾驶员期望值，避免驾驶员有过操纵的情况。同时从横摆角速度响应可以看到，未控制时的横摆角速度要比控制后激烈，质心侧偏角的响应则表明，经控制后质心侧偏角较控制前明显减小。

图7 双移线试验结果

4 结论

本文采用车辆响应偏差线性模型，设计了车辆稳定性LQR控制算法，得到了计算主动横摆力矩的反馈比例参数。并依据车辆动力学分析结果，设计了制动力施加决策和计算模块，实现了制动力的施加。采用Carsim和MATLAB建立了联合仿真平台，进行了开环和闭环试验，结果显示设计的算法能够有效地跟踪车辆二自由度模型响应，能够在车辆处于极限工况时提高车辆的操纵稳定性。

[1] 梅炜炜,高晓程,赵林峰,等.综合质心侧偏角和横摆角速度反馈主动转向控制[J].合肥工业大学学报(自然科学版),2020,43(12): 1601-1607.

[2] 郝正君,杨柳青.模糊逻辑控制的车辆稳定系统动力学仿真[J].中国工程机械学报,2018,16(04):332-336.

[3] E. Esmailzadeh, A. Goodarzi, G.R.Vossoughi. Optimal yaw moment control law for improved vehicle handling[J].Mechatronics,2003,13 (7):659-675.

[4] 丁海涛.轮胎附着极限下汽车稳定性控制的仿真研究[D].长春:吉林大学,2003.

[5] 龚天洋,谢宪毅,戎辉,等.基于相平面法的车辆电子稳定控制策略研究[J].交通信息与安全,2019,37(02):83-90.

[6] Hongtei Eric Tseng,Behrouz Ashrafi,Dinu Madau, etl. The Develop- ment of Vehicle Stability Control at Ford[J].IEEE/ASME Transatc- tions on Mechatronics,1999,4 (3):223-234.

[7] Ossama Mokhiamar, Masato Abe. Effects of model response on model following type of combined lateral force and yaw moment control performance for active vehicle handling safety[J].JSAE Review,2002(23):473–480.

[8] Ken Koibuchi, Masaki Yamamoto,Yoshiki Fukada, et al. Vehicle Stability Control in Limit Cornering by Active Brake[J].Internati- onal Congress & Exposition Detroit,960487.1996:26-29.

Design of Vehicle System Dynamics Control Algorithm Based on LQR Method

LONG Wen1, LIU Hao2

（1.Dongfeng Liuzhou Motor Co., Ltd., Passenger Car Technology Center, Guangxi Liuzhou 545005;2.Chongqing University of Technology, Chongqing 400054）

The vehicle stability control system can effectively improve the performance of the vehicle in the limit conditions, its active yaw moment application algorithm is the core of the system control. Based on two degree of freedom model of vehicle, using the linear model of vehicle response deviation, the LQR control algorithm of vehicle stability is designed and the active yaw moment feedback matrix is obtained. The decision-making and calculation module of wheel braking force is designed, and the input of vehicle control is obtained. The co simulation environment of CarSim and MATLAB is established, and the open-loop control tests such as lane change input and the sine input test and the closed-loop test of double lane change are carried out. The results show that the yaw rate of vehicle can effectively track the reference model value, and the sideslip angle of mass center is kept within stability region. The control algorithm designed in this paper can improve the stability control area of the vehicle and has a certain application value.

Vehicle Stability; Linear Quadratic Regulator; Yaw Rate; Side Slip Angle

U461

A

1671-7988(2021)23-76-05

U461

A

1671-7988(2021)23-76-05

10.16638/j.cnki.1671-7988.2021.023.021

龙文（1979—），男，本科，工程师，就职于东风柳州汽车有限公司乘用车技术中心，研究方向：底盘系统设计。