社会网络中基于节点平均度的k-度匿名隐私保护方案①

许佳钰, 章红艳, 许 力, 周赵斌

1(福建师范大学 数学与信息学院, 福州 350007)

2(福建省网络安全与密码技术重点实验室, 福州 350007)

近年来, 随着使用微博、Facebook、Twitter等社交网站的用户数快速增加, 产生 了大规模的社会网络数据. 这些数据具有巨大的商业价值和应用场景, 同样也包含了很多敏感信息[1]. 研究者开发出了大量的数据挖掘技术和社会网络分析方法, 用来挖掘和分析这些数据背后的价值. 但如果发布的数据被不正确使用, 用户可能会遭到恶意攻击和面临隐私泄露问题[2], 在数据挖掘的过程中需要保护用户隐私[3]. 民法典中也确立了平衡个人信息保护与信息合理使用之间的基本准则.因此, 对发布的社会网络数据进行隐私保护尤为重要[4],在发布数据的同时应该保护好个人隐私信息. 如何在有效地保护用户隐私的同时又能保证发布的数据具有可用性[5], 这是人们一直在研究的问题.

数据的隐私保护问题已经得到了广泛的研究,Sweeney[6]在2002年最早提出k-匿名模型, 而最近趋向于个性化的k-匿名[7]的研究. 在k-匿名模型提出之后, l-多样化[8], t-接近[9]等隐私保护模型也被先后提出.然而社会网络中的节点之间存在相关性, 如果仅对节点进行匿名处理, 攻击者仍可能会根据边权值或图结构对网络进行攻击[10-12]. 目前针对社会网络数据的隐私保护方法大致可分为基于聚类和基于图修改两种.

其中, 基于聚类的社会网络隐私保护方法是通过特定的聚类规则将一些节点和边进行聚类, 然后通过泛化达到匿名化效果. Hay等[13]提出对网络中相似节点进行聚合, 聚合后每个块中所包含的节点数n满足k≤n≤2k-1的条件, 这样使得攻击成功的概率不高于1/k. Skarkala等[14]使用节点聚类和边聚类相结合的方法对加权无向网络进行泛化, 以实现k-匿名. 姜火文等[15]利用属性图表示社交网络数据, 综合根据节点间的结构和属性相似度, 将图中所有节点聚类成一些包含节点个数不小于k的超点. 然而, 基于聚类的社会网络隐私保护方法将节点聚类成超点或将边聚类成超边会导致严重的边信息损失, 破坏网络结构, 大大降低数据可用性.

通过图修改的方法实现社会网络数据的隐私保护方法已成为近些年来研究者关注的热点. Liu等[16]首次提出图的k-度匿名化概念, 并采用增加边的图结构修改方式来实现图的k-度匿名化, 以抵抗节点度攻击.Chester等[17]首次提出一种加边与加点相结合的方法来实现k-度匿名图. 针对节点具有标签的社会网络, 文献[18,19]都提出了k-度-l多样化匿名模型, 该模型在满足k度匿名的基础上, 要求度数相同的k个节点至少要有l种不同标签, 并通过增加或删除边以及添加噪声节点的方法实现匿名. Casas-Roma等[20]采用穷举法和贪心算法生成度匿名序列, 通过邻居中心性边选择方法和随机边选择方法实现k-度匿名. 周克涛等[21]针对传统的k-度匿名方法添加的噪声数据过多, 提出了改进的基于邻居度序列相似度的k-度匿名保护方法,可以抵御以节点的度结合邻居度序列作为背景知识的攻击. Macwan等[22]提出了改进的k-度匿名方法, 该模型保留了网络结构属性以及用户隐私. Kamalkumar等[23]针对大规模社会网络提出快速的隐私保护方法, 对小社区实施个性化k-度匿名化. Kiabod等[24]引入一种节省时间的k-度匿名化方法, 该方法利用基于树结构计算图的匿名度序列, 利用基于匿名化级别对图形自底向上节点进行分区, 实现隐私保护级别的动态变化. 张晓琳等[25]针对大规模社会网络有向图, 提出了一种基于层次社区结构的大规模社会网络k-出入度匿名方法, 该方法提高了处理大规模社会网络有向图数据的效率, 并在匿名后保证了数据发布时社区结构分析的可用性. 以上这些基于图修改的社会网络隐私保护方法大多都采用添加、删除边或添加节点以及子图同构等扰动方式实现k-度匿名, 但这些方法还存在信息损失较为严重的问题.

针对以上两种方法存在的问题, 本文提出一种基于节点平均度的k-度匿名隐私保护方案, 用来解决社会网络数据的发布可能导致用户隐私泄露的问题, 在保护用户隐私的同时提高了发布数据的可用性. 本方案首先利用基于平均度的贪心算法生成k-度匿名序列, 然后采用优先保留重要边的图结构修改方法来对图进行修改, 实现图的k-度匿名化. 本方案不仅能有效地提高网络抵抗度攻击的能力, 还能克服传统方案在对网络匿名后所产生的信息损失严重的问题, 在保护用户隐私的同时提高了发布数据的可用性.

1 相关定义

在本文中, 用一个无向无权的图来表示社会网络,G=(V,E),V代表用户实体,E代表实体间的关系,V={v1,v2,···,vn} 是节点的集合,是边的集合且1 ≤i,j≤n.dG代表图G的度序列,d=[d1,d2,···,dn]. 其中,d(i) 或d(vi)代 表图中第i个节点vi的度.

定义1. 向量k-匿名. 如果整数向量V是k-度匿名的, 那么向量V中每个值都出现至少k次. 例如, 向量V=[5,5,3,3,2,2,2]是2-度匿名的.

定义2. 图的k-度匿名. 如果图G的度数序列d是k-匿名的, 那么图G= (V,E)是k-度匿名的.

显然, 只要找到原图的最优k-度匿名向量, 就可以根据该向量在原图基础上增补出新的k-度匿名图. 如图1(a)是一个没有进行过度匿名的原始图, 度序列为[2,3,3,5,3,2,4,3,3,2], 给定度序列和相应的节点ID序列.由于只有节点4具有度5, 而只有节点7具有度4, 所以任何人都可以重新识别出节点4和节点7. 将图1(a)匿名成图1(b), 度序列为[3,4,4,5,3,5,5,4,3,4], 变成一个3-度匿名图, 这时图中任何一个节点都至少有2个节点与其度数相同, 可以重新识别节点4或节点7的概率都减少到1/3.

图1 匿名前后对比图

因此, 如果一个图满足k-度匿名, 则表明图中任一个节点至少与其他k-1个节点具有相同的度, 利用节点度数作为背景知识的攻击者能够识别目标个体的概率不超过1/k[16]. 我们用k值这个指标来衡量社会网络的抵御攻击能力,k值越大, 目标个体身份被攻击者识别的概率就越小, 社会网络的抵御攻击能力就越强, 隐私保护程度也就越高.

根据以上定义, 为了将输入图G转换为结构上类似于G的k-度匿名图, 我们首先需要将G的度序列d转换成k-度匿名序列, 然后根据度匿名序列对G进行图结构修改构造出, 我们在图结构修改时是通过增加、删除或者交换边来实现节点度数的调整. 以单纯对边进行操作, 不增加节点的策略为例, 我们希望选择边变化最少(度数变化最少)的方案来实现k-度匿名,这样可以保证匿名前后图结构的相似性.

定义3. 基于平均度的图匿名代价. 图匿名代价可用匿名前后边的变化数来计算, 根据握手定理可知一条边贡献两个度, 即匿名前后度的总变化数刚好是边的总变化数的两倍, 因此边的变化数与度的变化数直接相关.

图匿名代价GA(G,)由式(1)计算得到:

对于i＜j, 节点i到j之间的所有节点的平均度为d(a), 由式(3)计算得到:

如果节点i到j之间的所有节点形成同一个匿名组, 同一组中所有节点的度都匿名成该组所有节点的平均度d(a), 则有式(4)成立:

将该组的匿名代价记为I(d[i,j]),则基于节点平均度的k-度匿名代价由式(5)计算得到:

在进行图修改操作时要实现式(5)的最小化, 以保持数据可用性.

2 社会网络的k-度匿名隐私保护方案

本节提出了一种基于节点平均度的k-度匿名隐私保护方案, 方案主要包括度匿名序列生成和图结构修改两个阶段. 首先利用基于平均度的贪心算法对社会网络节点度序列进行划分, 生成k-度匿名序列； 然后根据生成的k-度匿名序列对图进行修改实现图的k-度匿名化, 修改时采用优先保留重要边的图结构修改方法.与传统方案相比, 在对图结构的修改程度一样的前提下, 本方案可以达到更大的k值, 说明本方案相对传统方案的抵御攻击能力有显著提高, 提供了更强的隐私保护.

本文中的符号说明见表1.

表1 符号说明

2.1 度匿名序列生成

本方案利用基于平均度的贪心算法(算法1)生成原始图的k-度匿名序列.

下面给出了生成k-度匿名序列的算法.

算法1. k-度匿名序列生成算法输入: 原始图G, 正整数k ˆd输出: k-度匿名序列1. d←degree sequence of G 2. sort(d)3. put the first k nodes into group gi 4. i = 1 5. while until every node gets the group do 6. count Cmerge, Cnew 7. if Cmerge＞ Cnewthen 8. i++9. put nodes nk+1 ～n2k into new group gi 10. k = k + 2k 11. else 12. put node nk+1 into group gi 13. k = k + 1 14. end if

15. count da(gi)//计算的平均度16. the degree of node in gi becomes da(gi)17. end while

该算法将社会网络图G和整数k作为输入, 首先找到输入图G的度数序列并将其按度数降序的顺序进行排序, 然后将前k个节点放入同一组, 接着分别根据式(6)和式(7)计算比较Cmerge和Cnew两个成本, 来决定应该将第(k+1)个节点合并到当前的分组中, 还是在位置(k+1)处开始一个新组. 其中Cmerge表示把第(k+1)个节点合并到当前分组所产生的成本, 由式(6)计算得到；Cnew表示把第(k+1)个节点放入一个新的分组所产生的成本, 由式(7)计算得到.

当Cmerge＞Cnew时, 将第k+1～2k的节点放入一个新的分组, 然后计算和比较第2k+1个节点的成本并放入相应的分组中, 以此类推.

当Cmerge＜Cnew时, 将第k+1个节点合并到上一个分组, 然后计算和比较第k+2个节点的成本并放入相应的分组中, 以此类推.

直到将所有节点分完组后, 计算每一个分组中节点的所有节点的平均度d(a), 然后令该组中所有节点的度都变为平均度, k-度匿名序列生成.

2.2 图结构修改

在上一节中, 原始图的度序列已经被匿名成为k-度匿名序列. 根据生成的k-度匿名序列对图结构进行修改, 使得修改后的匿名图的度序列满足匿名要求.

本方案中进行图结构修改时对边的操作方式主要包含以下3种:

(1)边增加策略: 如图2所示, 我们选择两个不同节点vi,vj∈V, 若(vi,vj)∉E, 可以在节点vi,vj之间添加一条边(vi,vj), 两个节点的度同时增加1； 若(vi,vj)∈E,此时需要找到节点vi的不相邻节点集合(vi), 以及vj的不相邻节点集合(vj), 在(vi)和(vj)中分别找到两个节点vp,vq满足(vp,vq)∈E, 删除边(vp,vq),同时增加边(vp,vi) 与 边(vq,vj) ,此时我们可以看出两个节点vi,vj的度同时增加1, 而节点vp,vq的度没有变化, 并且增加了一条边.

图2 边增加策略的方式

(2)边删除策略: 如图3所示, 我们选择两个不同节点vi,vj∈V, 若(vi,vj)∈E, 此时我们可以在节点vi,vj之间删除边(vi,vj), 两个节点的度同时减1； 若(vi,vj)∉E,此时我们需要找到节点vi的相邻节点集合Γ (vi), 以及vj的相邻节点集合Γ (vj). 在Γ (vi)和 Γ (vj)中分别找到两个节点vp,vq满足(vp,vq)∉E, 增加边(vp,vq), 同时删除边(vp,vi) 与 边(vq,vj) . 此时节点vi,vj的度同时减少1, 而vp,vq的度没有变化, 并且减少了一条边.

图3 边删除策略的方式

(3)边交换策略: 如图4所示, 在边交换策略中,(vj,vp) 与 (vi,vj)∉E这两种情况的边操作是一样的, 需要同时对3个点进行操作. 如果vi,vj,vp∈V, 且同时满足(vi,vp)∈E和(vj,vp)∉E, 此时删除边(vi,vp), 增加边(vj,vp), 节点vi的度减少1, 而节点vj的 度增加了1,vp的度和边数没有变化.

图4 边交换策略的方式

原始图中节点v的度数d(v)与其所属分组的平均度数d(a)之间可能存在的大小关系有如下3种情况:

(1)当d(v)＜d(a) 时 , Δd(v)＞0 , 节点v需要通过执行边增加策略使节点度数增加.

(2)当d(v)＞d(a) 时 , Δd(v)＜0 , 节点v需要通过执行边删除策略使节点度数减少.

(3)当d(v)=d(a) 时, Δd(v)=0 , 节点v满足匿名化,不需要进行任何操作.

我们在进行图结构修改时只需考虑还未满足度匿名化的节点, 对于满足度匿名化的节点可直接跳过无需进行任何操作. 对于还未满足度匿名化的节点, 需要根据两个点间的度数大小关系以及有无连边的情况选择相应的图修改策略.

任意两个节点vi,vj, 两者都满足Δd(v)＜0, 则需要执行图2中的边增加策略, 还需根据两个节点之间是否存在边选择相应的操作方式. 当两个节点之间不存在边时, 则选择操作方式如图2(a)； 当两个节点之间存在边时, 则选择操作方式如图2(b).

任意两个节点vi,vj, 两者都满足Δd(v)＞0, 则需要执行图3中的边删除策略, 还需根据两个节点之间是否存在边选择相应的操作方式. 当两个节点之间不存在边时, 则选择操作方式如图3(a)； 当两个节点之间存在边时, 则选择操作方式如图3(b).

任意两个节点vi,vj, 其中一个满足Δd(v)＞0, 另一个满足Δd(v)＜0时, 则需要执行图4中的边交换策略,无论两个节点之间是否存在边, 操作方式都是一样的.

在边操作中选择边的时候, 要考虑保留重要的边,方案中我们利用了邻域中心性(Neighbourhood Centrality,NC)值来量化大型网络的边缘相关性[20]. 边(vi,vj)的邻域中心性定义为同时与vi或vj相邻, 但不同时与vi和vj相邻的节点的比例, 由式(8)计算得到:

NC值越小, 说明该边的边相关程度就越低, 该边的重要程度比较低；NC值越大, 说明该边的边相关程度就越高, 该边的重要程度比较低. 为了降低图修改前后的信息损失量, 本方案在进行边操作时选择NC值较低的边.

本方案的算法在执行时会多次遍历, 直达图结构修改完成, 具体的图结构修改算法如算法2所示.

算法2. 图结构修改算法输入: 原始图G, 原始图度序列d, k-度匿名序列ˆG输出: k-度匿名图 1. while True do Δd=ˆd-d 2. sort(|Δd|)3. vi=|Δd|max 4. pick node |Δd|vj≠0 5. pick node vj randomly, Δdvj＞0 Δdvj＞0 6. if and then 7. if there exits (vi,vj) then vp,vq∉Γ(vj)vp,vq∉Γ(vj)8. pick two nodes vp,vq randomly (exits (vp,vq) and and )9. delete (vp,vq), add (vi,vp), add (vj,vp)10. else 11. add (vi,vj)Δdvi++,Δdvj++12. 13. end if Δdvi＜0 Δdvj＜0 14. if and then 15. if there exits (vi,vj) then 16. delete (vi,vj)17. else vp∈Γ(vi)vq∈Γ(vj)18. pick two nodes vp,vq randomly (not exits (vp,vq) and and )19. delete (vi,vp), delete (vj,vq), add (vp,vq)Δdvi--,Δdvj--20. 21. end if Δdvi＜0 Δdvj＞0 22. if and then vp∈Γ(vi) vp∉Γ(vj)23. pick node vp randomly ( and )24. delete (vi,vp), add (vj,vp)Δdvi--,Δdvj++25. Δdvi＞0 Δdvj＜0 26. if and then vq∉Γ(vi) vq∈Γ(vj)27. pick node vq randomly ( and )28. add (vi,vp), delete (vj,vp)Δdvi++,Δdvj--29. 30. end while

在上述算法中, 将原始图G和匿名前后的度序列作为输入, 首先计算每个节点需增加的度数| Δd(v)|, 这个过程的时间复杂度为O(n), 并对其进行降序排序, 排序过程的时间复杂度O(nlog2n). 然后选取| Δd(v)|值最大的节点vi和| Δd(v)|值 非零的节点vj, 判断vi与vj之间的度数关系以及有无连边, 执行相应的边操作, 并更新两个节点相应的Δd(v)值, 这个过程的时间复杂度为O(1).根据更新后的Δd(v)值继续选择操作的节点, 重复以上步骤, 直到所有节点的Δd(v)值为0, 则图结构修改完成,总重复次数为O(n)级别. 因此, 该算法的总时间复杂度为O(n2)级别. 但是在真实社交网络中 算法仍有较好的执行效率, 能够满足实际需求.

3 实验结果分析

本方案使用Facebook数据集进行仿真实验, 来源于 Stanford大学的一个公开数据库SNAP[26], 该数据集说明了Facebook社交网站上的各个用户之间的关系,包含节点数4039个, 无向边88 234条, 节点的总度数为176 468度, 平均度数为43度, 且节点的度服从幂律分布. 算法代码用Python编程实现, 实验环境为Intel Core i5 CPU 1.4 GHz, 16 GB内存, 操作系统为 MacOS.

对于社会网络中的图数据, 在进行匿名隐私保护的同时保持其可用性是非常重要的[10]. 为了说明本文提出的k-度匿名隐私保护方案的有效性, 我们通过计算边的变化率来说明数据的信息损失量, 其中边的变化率为匿名前后边的变化数与原始图中的边总数之比.数据的信息损失量越小, 则数据的可用性越好. 另外我们还考虑了图结构的一些基本属性, 主要测试平均聚类系数、平均最短路径、节点平均度这3个指标. 单个节点的聚类系数是它所有相邻节点之间连边的数目占可能的最大连边数目的比例, 而整个网络的平均聚类系数就是所有节点簇系数的平均值； 平均最短路径是网络中所有结点对的距离的平均值； 节点平均度是网络中所以节点的度数之和与节点总数之比. 我们将实验前的数据与进行k-度匿名后的数据进行对比, 同时与文献[16,20]的方案进行对比来, 以验证本方案的有效性.

图5展示的是本方案和文献[16,20]的方案在匿名前后信息损失量的变化结果, 表2是具体的实验数据. 通过对比分析在匿名前后网络的边变化率来衡量信息损失量. 如图5所示, 随着k值的增大, 3种方案造成的信息损失量也都跟着变大, 但是相比于文献[16,20]两种方案, 本方案信息损失量是最小的, 更好地保持了数据的高可用性.图6展示了本方案和文献[16,20]方案在匿名前后聚类系数的变化结果, 表3是具体的实验数据. 如图6所示, 与文献[16,20]两种方案相比, 本方案使得匿名后的网络在不同的k值下始终最接近于原始网络的平均聚类系数值, 对网络平均聚类系数的影响明显小于另外两种方案. 文献[16]的方案在图结构修改时没有考虑保留重要的边, 使得匿名后网络的平均聚类系数与原始网络相比有较大改变, 对图结构的修改较大. 而本方案在图结构修改时引入了NC值来保留重要的边, 匿名前后图结构变化非常小. 由此可见, 本方案在实现k-度匿名保护用户隐私同时, 还能保持数据具有较高的可用性.

图5 信息损失量对比图

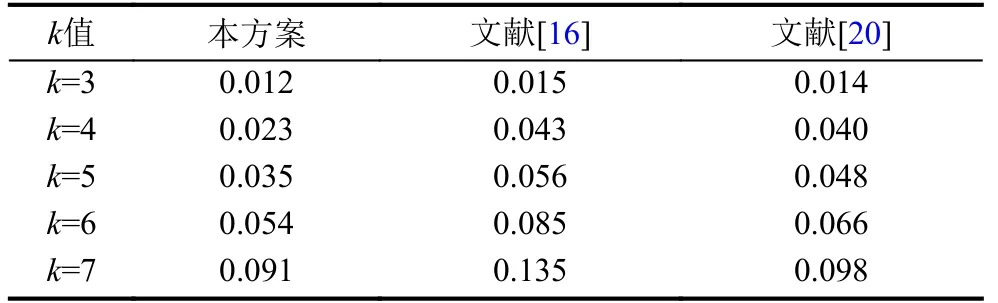
表2 信息损失量对比

图6 平均聚类系数对比图

表3 平均聚类系数对比

图7展示的是本方案和文献[16,20]的方案在匿名前后平均最短路径的变化结果, 表4是具体的实验数据.如图7所示, 随着k值的增加, 3种方案的平均最短路径都在减小, 但是文献[16]的方案使得匿名后网络的平均最短路径始终大于原始网络, 较大程度地破坏了网络结构. 当k值较小时, 文献[20]的方案使得匿名后网络的平均最短路径始大于原始网络, 对网络结构的破坏较大；当k值较大时, 文献[20]的方案使得匿名后网络的平均最短路径始小于原始网络, 对网络结构的破坏较小. 而本方案使得匿名后网络的平均最短路径始终小于原始网络, 较好地保持了网络结构的稳定性.

图7 平均最短路径对比图

表4 平均最短路径对比

图8展示的是本方案和文献[16,20]的方案在匿名前后节点平均度的变化结果, 表5是具体的实验数据. 如图8所示, 随着k值的增加, 本方案对原始网络节点平均度的改变量最小, 匿名后网络的节点平均度数与原始网络基本相同. 文献[20]的方案对原始网络节点平均度的改变程度略高于本方案. 文献[16]的方案使得匿名前后网络的节点平均度有较大改变, 对原始网络结构的破坏较为严重.

表5 节点平均度对比

图8 节点平均度对比图

图9展示了本方案和文献[16,20]的方案在运行时间上的比较结果, 表6是具体的实验数据. 如图9所示, 当k值较小时, 3个方案的算法运行时间大致相同,当k值较大时, 本方案的运行时间要高于文献[16,20]的方案. 但总体来说, 本方案的运行时间不会比另外两个方案高出很多, 且本方案使得社会网络在抵御度攻击方面和保持图数据可用性方面均有了较好的改进,因此这样稍高的时间复杂度还是在可接受范围内.

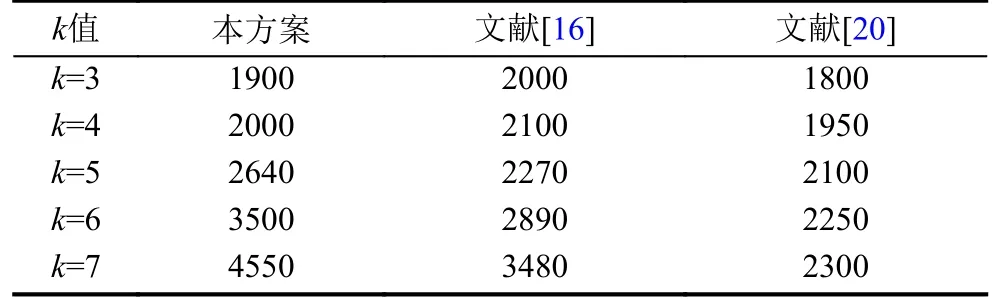
表6 执行时间对比(s)

图9 执行时间对比图

4 结束语

针对社会网络数据的发布可能遭到度攻击进而导致用户隐私泄露的问题, 本文提出一种基于节点平均度的k-度匿名隐私保护方案, 本方案在保护用户隐私的同时保证了发布的数据具有较高可用性. 首先利用基于平均度的贪心算法对社会网络节点度序列进行划分, 使得同一分组中节点的度都修改成平均度, 生成k-度匿名序列, 极大地减少了与原始度序列的距离； 然后使用边增加、边删除、边交换3种边操作方式对原始图进行图结构修改, 由于对边进行操作时考虑了NC值, 保留了网络中重要的边, 匿名后的网络保持了较好的连通性和关系结构, 从而提高了发布数据的可用性.本方案不仅能有效提高社会网络抵御度攻击的能力,还能保持网络结构的高稳定性和发布数据的高可用性.但是在算法的时间复杂度方面, 与其它方案相比优势不够明显, 因此还需要在未来进一步研究如何减小算法的时间复杂度.