基于二维最小相位相干因子的MIMO穿墙雷达成像方法*

屈乐乐，杨永席，杨天虹

(沈阳航空航天大学 电子信息工程学院,沈阳 110136)

0 引 言

超宽带(Ultra-wideband,UWB)雷达是一种高分辨率雷达，在分辨率、穿透能力等方面具有许多传统探测方法不具备的优势。多输入多输出(Multiple-Input Multiple-Output,MIMO)雷达是通过多个发射端发射特定波形、多个接收端接收各路散射信号并进行联合处理的新体制雷达，可以在阵元数目有限的情况下极大地提高阵元利用率。因此，超宽带MIMO被越来越广泛的应用在穿墙雷达中[1-2]。

对于穿墙成像雷达而言，低栅瓣、低旁瓣和高分辨率的图像有助于区别不同的目标，抑制伪影。文献[3]系统地比较了超宽带与窄带信号，指出栅瓣是由各阵元发射的信号部分相干叠加形成的，对于超宽带信号，阵元均匀配置的阵列比随机阵列的栅瓣低。文献[4-5]分析了MIMO雷达因等效相位中心产生的误差，并给出相应的误差校正方法。对于阵列设计，文献[6]提出分解法设计收发分置阵列，使得等效阵列是均匀无冗余且等幅加权的，但会遗漏一些设计方案。文献[7]根据给定的等效阵列设计阵元的位置及权重，用卷积逆运算配置收发共置阵列。文献[8]提出了一个基于多项式分解方案，并将其应用于具有均匀线性的等效天线阵列设计。

正确的MIMO阵列拓扑设计可以减少成像结果的栅瓣和旁瓣杂波干扰，提高成像质量。但在实际应用中系统天线尺寸在很多情况下不能满足理论上完全消除栅瓣的天线间距大小。另外，电磁波通过墙体传播会出现折射、多次反射以及速度变化等现象，导致虚假目标伪影的产生。这些都会导致成像结果存在一定的栅瓣和旁瓣干扰[9-10]，因此寻找有效的成像方法提高成像质量很有必要。

为提高成像质量，可以采用相干因子(Coherence Factor,CF)和相位相干因子(Phase Coherence Factor,PCF)对成像结果进行加权处理[5,10-12]。CF和PCF在方位向上均具有较好的栅瓣旁瓣抑制作用，但两者都无法抑制距离向的旁瓣干扰。文献[11]提出距离向相干因子(Range Coherence Factor,RCF)，RCF沿频率维度而不是孔径维度做非相干求和，可实现在距离向上抑制旁瓣。文献[12]提出了二维相位相干因子(Two-dimensional Phase Coherence Factor,2D PCF)，可同时抑制方位向和距离向的栅瓣和旁瓣干扰。

本文首先针对文献[9]分解方案中阵元位置不会发生改变的问题引入了位移因子，对虚拟阵元、发射阵元和接收阵元位移因子的关系进行了描述，得到了简便可行、配置灵活的MIMO阵列配置方法；然后推导了PCF、RPCF和2D PCF三种成像加权因子，针对2D PCF仅综合PCF和RPCF部分优点的情况，提出了二维最小相位相干因子(Two-dimensional Minimum Phase Coherence Factor,2D MPCF)，可以更加充分地利用PCF和RPCF的优点；最后通过仿真实验验证了2D MPCF无论在方位向还是距离向拥有比2D PCF更好的干扰抑制效果。

1 MIMO阵列配置方法

1.1 分析模型

根据相位中心近似原理将双站雷达等效为收发同置的单站雷达，其模型如图1所示。

图1 相位中心近似模型

虚拟阵元位置可以表示为

CV={rV:rV=(rT+rR)/2,rT∈ST,rR∈SR}。

(1)

式中：rV代表等效虚拟阵元所在位置，rT和rR分别表示发射和接收阵元所在位置，ST和SR是包含发射和接收阵元位置向量的集合。阵元相应的权值为

wV(rV)=wT(rT)·wR(rR)。

(2)

式中：wV(rV)、wT(rT)和wR(rR)分别是虚拟阵元、发射阵元和接收阵元的权值。在本文中对阵列的设计是基于均匀无冗余的等效阵列，相应权值wT(rT)和wR(rR)均设为1。

1.2 阵列配置方法

1.2.1 计算等效孔径长度和虚拟阵元个数

方位向分辨率与等效孔径长度之间的关系为

(3)

式中：L为等效孔径长度,λc为中心频率对应的波长,ρ为阵列中垂线上与阵列垂直距离为R处的方位向分辨率。等效虚拟阵元个数与栅瓣电平的关系为

(4)

式中：SL表示栅瓣电平，M为等效虚拟阵元个数。

1.2.2 因式分解法设计MIMO阵列

因式分解对次幂的运算操作仅有加减，所以将式(1)改写成

CV={rV:2rV=rT+rR,rT∈ST,rR∈SR}。

(5)

此时rT+rR的位置可表示为

(6)

根据文献[8]中的方法，如果M可以分解为Q个不可约的正整数，即

(7)

则PM(z)可以表示为

(8)

(9)

对虚拟阵元位置的改变可以通过引入一个位移因子，则改变后的虚拟阵元位置为

PMs(z)=PM(z)·zm。

(10)

式中：zm=zmT·zmR，这里zmT和zmR分别是发射阵元与接收阵元的位移因子。

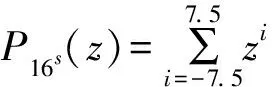
P16s(z)=(1+z)(1+z2)(1+z4)(1+z8)·z-7.5。

(11)

则MIMO阵列的其中一个方案为

(12)

需指出的是，当Q个不可约的正整数不完全相等且排序不同时，其分解方案也是不同的。

1.2.3 确定最终的阵列配置

阵列配置分解出来后，可以根据要求选择合适的阵列配置，通常考虑利用最小的空间来实现相同的有效孔径。

2 基于2D MPCF加权的成像方法

2.1 频域后向投影算法

图2中的MIMO雷达阵列包含a个发射阵元和b个接收阵元，在该成像场景下发射和接收阵元位置分别表示为rTe(e=1,2,…,a)和rRf(f=1,2,…,b)，目标点位置为rp。从第e个发射阵元经过墙到目标点，再从目标点经过墙到第f个接收阵元的路径如图2所示。

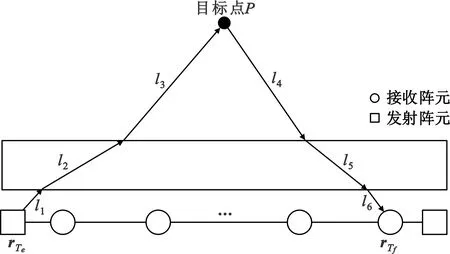
图2 穿墙成像几何示意图

则第ef个通道对应的接收信号为

(13)

式中：A表示目标点的反射系数；N代表频点个数；fk是第k个频率；τef为传播时延，

(14)

式中：c是光速,v是电磁波在墙体中的传播速度，l1～l6为电磁波的传播路径。

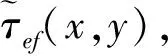
(15)

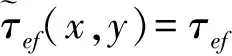
(16)

2.2 2D MPCF因子

PCF方法最早应用于超声成像技术,是一种基于孔径数据瞬时相位统计分析的自适应波束形成算法。穿墙成像中像素点(x,y)在第ef个通道的瞬时相位为

φef(x,y)=∠Sef(x,y) ，

(17)

则PCF定义为

PCF(x,y)=1-std(exp(jφef(x,y)))。

(18)

式中：std表示求标准差，

(19)

式中：φef是φef(x,y)的简写。当成像点与目标点位置相同时，瞬时相位的标准差为0，PCF的值为1。将PCF作为加权因子对图像各像素点进行加权为

Ipcf(x,y)=I(x,y)·PCF(x,y)。

(20)

通过上述公式可知，PCF求瞬时相位的标准差是沿孔径维度，仅在方位向具有良好的栅瓣旁瓣抑制效果，但无法抑制距离向旁瓣干扰。为实现在距离向上抑制旁瓣，可在频率维度求瞬时相位的标准差得到RPCF：

RPCF(x,y)=1-std(exp(jφk(x,y)))。

(21)

其中每个频点的瞬时相位为

φk(x,y)=∠Sk(x,y) ，

(22)

(23)

将RPCF作为加权因子对图像进行加权为

Irpcf(x,y)=I(x,y)·RPCF(x,y)。

(24)

在PCF和RPCF的基础上，文献[12]提出了2D PCF，其定义为

PCF2D(x,y)=PCF(x,y)·RPCF(x,y)。

(25)

2D PCF因子不仅可以在方位向抑制栅瓣干扰，而且可以在距离向抑制旁瓣干扰。为了更加充分地利用PCF和RPCF的优点得到更好的栅瓣旁瓣抑制效果，本文提出了2D MPCF，其定义为

MPCF2D(x,y)=min{PCF(x,y)，RPCF(x,y)}2。

(26)

将其作为加权因子对图像进行加权为

Impcf2D(x,y)=I(x,y)·MPCF2D(x,y)。

(27)

图3为基于2D MPCF成像方法的流程图。

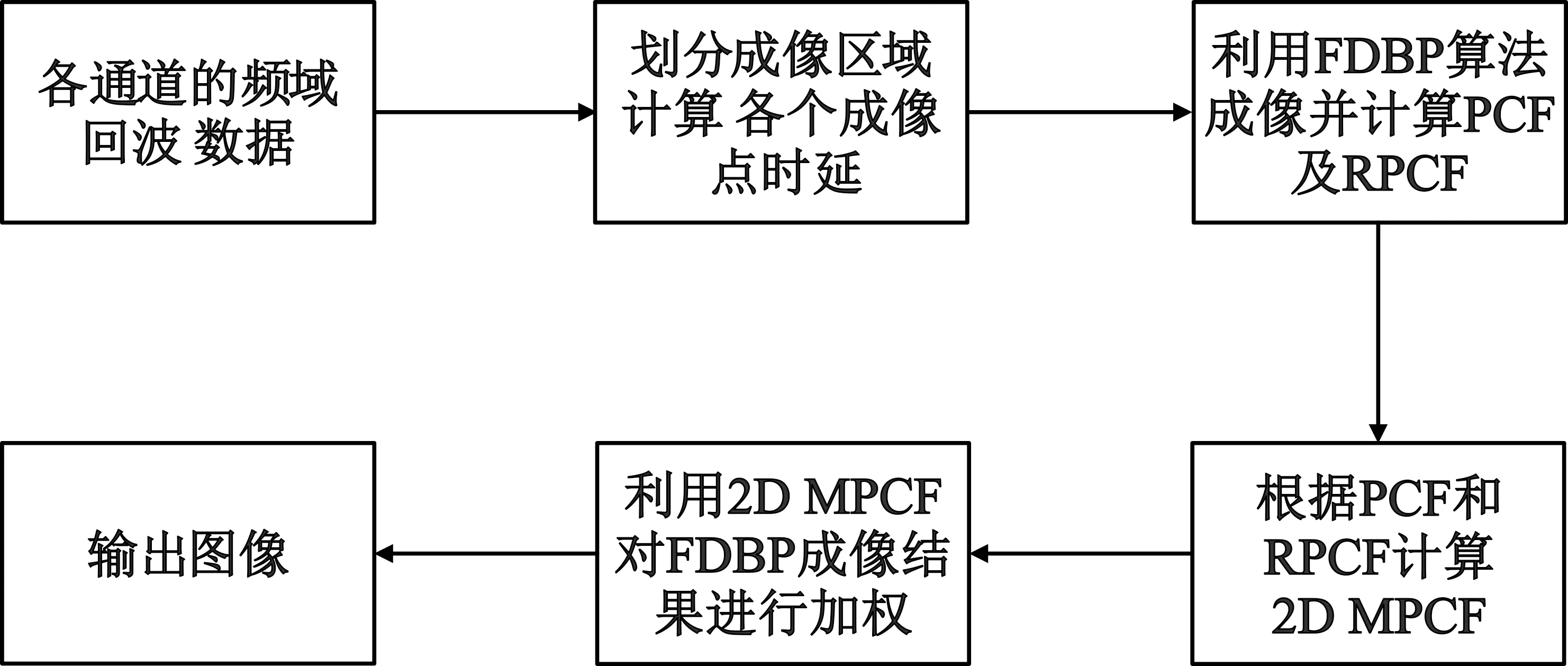
图3 基于2D MPCF成像方法的流程图

3 实验仿真

本次仿真设阵列中心3 m处方位向分辨率为0.1 m，栅瓣水平小于-30 dB，中心频率2 GHz，分数带宽为100%。

采用第1节中的步骤，计算得到等效孔径长度L=2.25 m，等效阵元个数M>31。因此选取等效阵元个数为32个，通过计算并保留两位小数后得到d=0.15 m。其因式分解结果为

P32s(z)=(1+z)(1+z2)(1+z4)(1+z8)(1+z16)·z-15.5。

(28)

按照4发8收的配置进行组合，可以得到多种组合方案，其占用空间最小的方案为

(29)

该方案的MIMO阵列模型如图4所示，阵列总长为2.55 m。

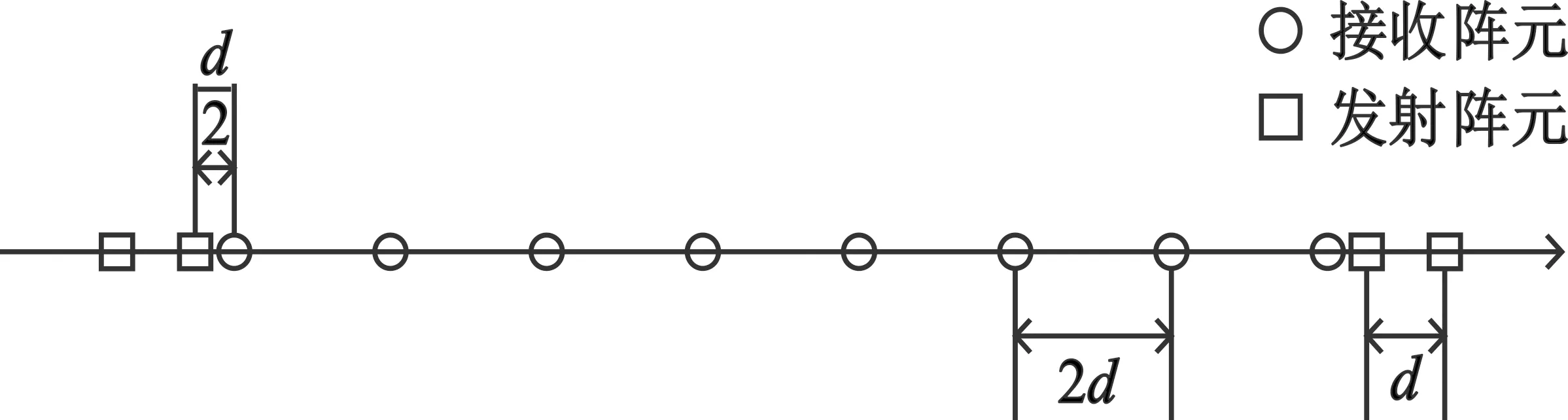
图4 长度最小的4发8收MIMO阵列

仿真实验场景如图5所示，MIMO阵列平行于x轴，中心位于(2.5 m,0.1 m)处，发射中心频率为2 GHz的Ricker波，时窗为50 ns。墙体平行于x轴，中心为(2.5 m，0.6 m)，墙体厚度为0.2 m，长度为5 m，电导率为0.01，相对介电常数为7.6。目标1和目标2分别是圆心位于(1.7 m，3 m)和(3.4 m，3 m)处、半径为0.1 m的圆形金属目标。

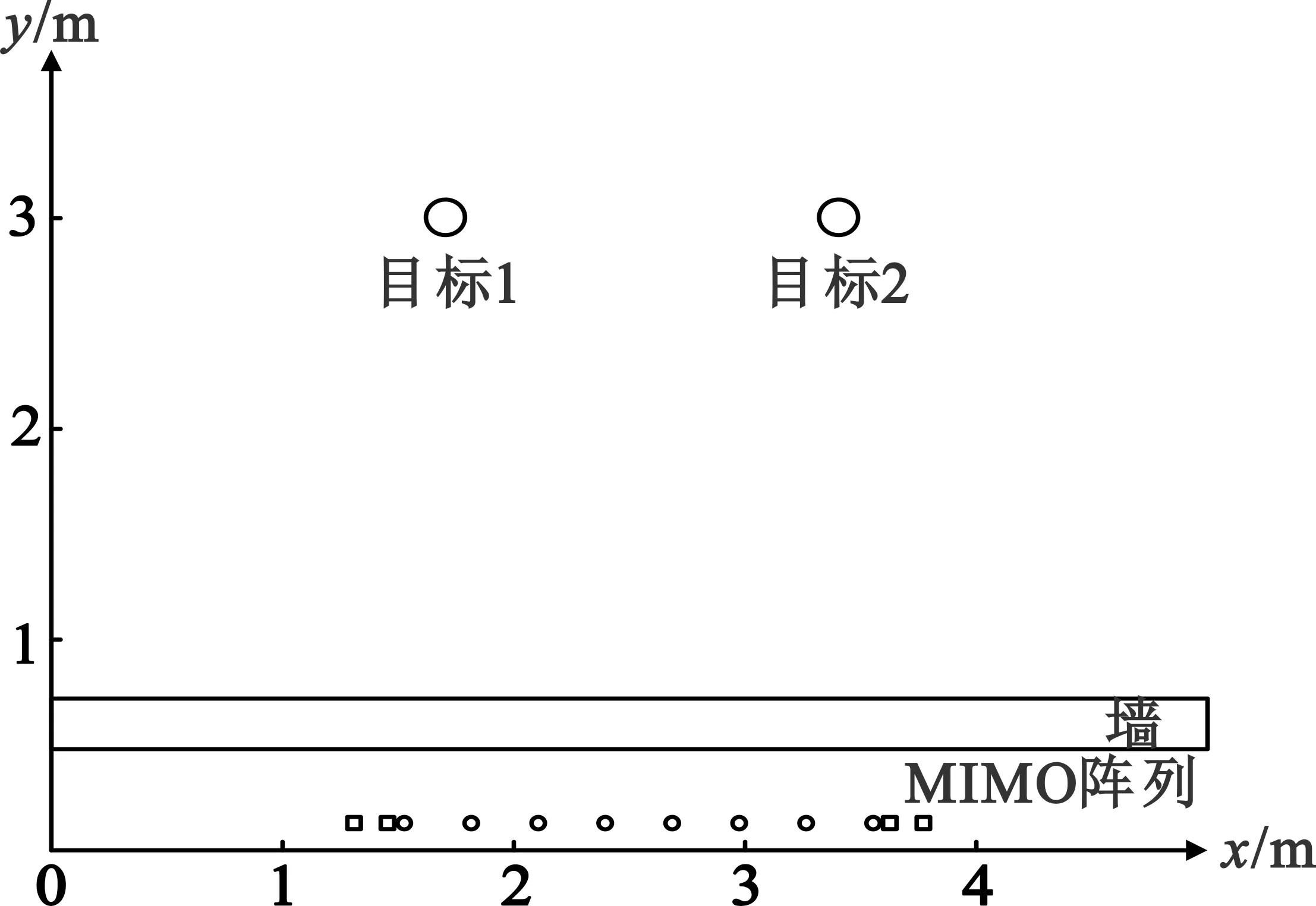
图5 仿真场景

采用基于时域有限差分方法的GprMax软件[13]得到时域回波数据。由于成像方法和加权因子是在频域进行，采用傅里叶变换技术将仿真产生的时域数据变换到频域。在每个通道得到带宽为1～3 GHz、频率步长为20 MHz的101个频点回波数据。成像区域大小为3 m×3 m，其中方位向1～4 m，距离向1.5～4.5 m，共划分为300×300个网格，利用FDBP成像算法对频域数据进行处理得到如图6所示的成像结果。

图6 FDBP成像结果(dB显示)

图6中红色圆圈是因为墙体多次反射所引起的伪影。分别利用2D PCF和2D MPCF对FDBP成像结果进行加权，得到图7所示的成像结果。

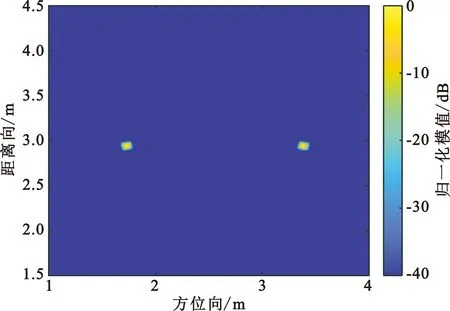
(b)2D MPCF加权图7 成像结果(dB显示)

为了定量描述杂波抑制的效果，使用积分旁瓣比(Integrated Side Lobe Ratio,ISLR)对成像质量进行评价。ISLR定义为

(30)

式中：Etotal和Emain分别是图像的总能量和目标主瓣能量。图7(a)和图7(b)的ISLR分别为-87.54 dB和-115.48 dB，2D MPCF加权图像的ISLR比2D PCF的ISLR降低了27.94 dB。

为了更好地观察两种因子对杂波的抑制作用，图8给出了两种因子加权后图像中峰值点位置在方位向和距离向的剖面图。

(a)方位向

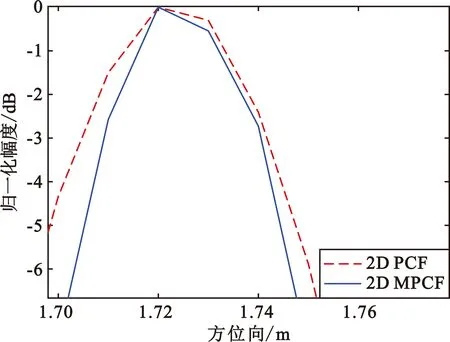
(b)(a)的局部放大

(c)距离向

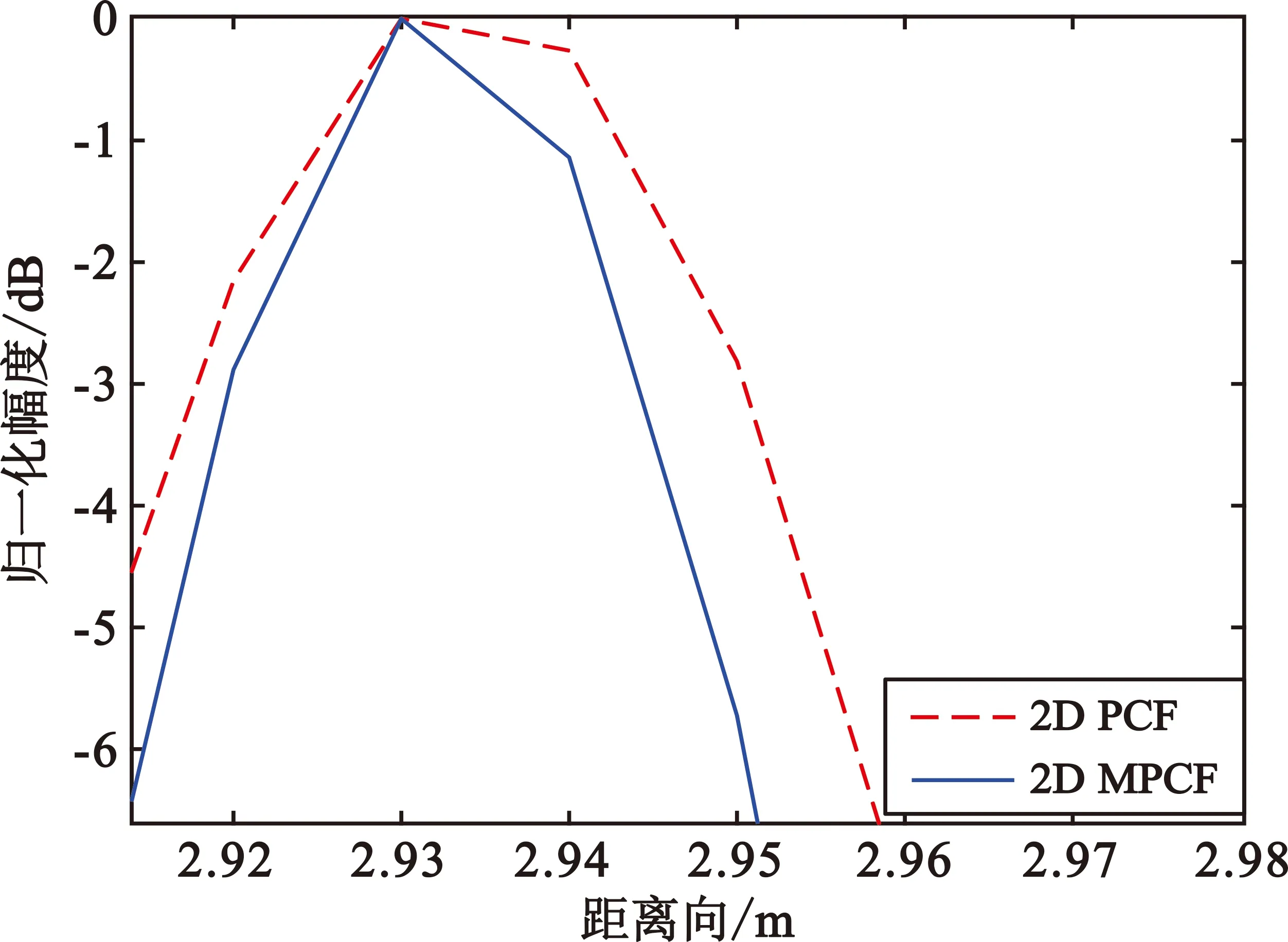
(d)(c)的局部放大图8 峰值处方向位与距离向剖面图

将峰值点附近区域放大显示如图8(b)和图8(d)所示，在图8(b)中-3 dB宽度从4个像素降低为3个像素，在图8(d)中-3 dB宽度从4个像素降低为3个像素。这说明2D MPCF加权后比2D PCF加权后在两个方向上获得了更好的分辨率。2D MPCF和2D PCF都是将PCF和RPCF进行结合的成像方法，因为PCF和RPCF对各个通道相位信息处理方式的不同，造成了其在不同方向上对栅瓣和旁瓣杂波干扰抑制效果不同。在理想情况下，PCF和RPCF在目标点位置得到的值均为1，但在目标点以外，因为抑制效果不同对应的PCF和RPCF的值也会有所不同。2D PCF仅是将PCF和RPCF的值进行简单的相乘，在抑制效果不同的点，简单的相乘便没有充分利用这种因对各个通道相位信息处理方式的不同而带来的优点，2D MPCF便考虑到了这种情况，因此可以在两个方向上获得更好的效果。

4 结束语

本文介绍了一种基于因式分解法的超宽带穿墙雷达MIMO阵列配置方法，使用该方法可以快速准确设计出MIMO阵列并对收发阵列的位置可以进行调整，从而获得拥有较低栅瓣水平的MIMO阵列；然后提出了基于2D MPCF加权的穿墙雷达MIMO成像重建方法。仿真实验结果表明，基于2D MPCF加权的穿墙雷达MIMO成像重建方法在方位向和距离向具有更优异的杂波抑制能力，并在一定程度上提高了成像重建分辨率。下一步将提高成像算法的计算效率，满足穿墙雷达实时成像场合的需求。