基于不同本构模型的面板堆石坝应力变形分析
2022-01-04黄小华
黄小华
(福建水利电力职业技术学院,福建 永安 366000)
混凝土面板堆石坝指用碎石和砂砾石经过抛填、碾压成型的一种坝型。因其具有断面小,施工简单,造价较低,对地形地质的要求较低等特点,因此是坝工界应用较广泛的一种坝型。随着面板堆石坝设计施工技术的快速发展,大坝主体的填筑质量得到改善,坝体的高度也得到快速的提升。对于高面板堆石坝,变形量偏大、稳定期偏长、变形控制是大坝建设的难点之一。由于筑坝材料的应力应变关系对于数值模拟分析影响很大,因此,分析混凝土面板堆石坝在不同本构模型下的应力变形规律具有重要意义。
1 堆石料的本构模型
目前,在国内外坝工界,混凝土面板堆石坝有限元分析中,堆石料本构模型主要采用两种类型:非线性弹性模型和弹塑性模型[1]。前者在广义胡克定律的基础上建立刚度矩阵,假设变形全部为弹性的,以及通过改变弹性常数的数值来反映筑坝材料的非线性。该类模型常见的有邓肯E-v模型、邓肯E-B模型和K-G模型。由于筑坝材料变形非完全弹性特性,而是具有典型的弹塑性特性,因此,在混凝土面板堆石坝数值计算中,筑坝材料采用弹塑性模型从理论上讲更合理。沈珠江双屈服面模型和剑桥弹塑性模型是目前坝工界常用的两种弹塑性模型。
1.1 邓肯E-v模型
邓肯等1963年首先提出可以采用增量弹性模型拟合黏性土和砂性土的应力应变关系。该模型的切线弹性模型的表达式为:
(1)
式(1)中:K—初始模量系数;
Pa—大气压力,MPa;
n—初始模量指数;
σ1—大主应力,MPa;
σ3—小主应力,MPa;
Rf—破坏比;
c—堆石料的粘聚力,MPa;
φ—堆石料的内摩擦角,(°)。
对卸荷—再加荷模量Eur与σ3的关系仍以幂函数表示,其形式为:
(2)
式(2)中:Eur、nur均为试验参数。
切线泊松比的表达式为:
(3)
式(3)中:G、D、F均为与泊松比有关的模型参数。
1.2 邓肯E-B模型
由于邓肯E-v模型计算值υt偏大,且求G、F、D值时带有不定性,与试验资料拟合不理想。邓肯等又提出采用切线体积变形模量Bt代替切线泊松比υt。Bt的表达式如下:
(4)
式(4)中:Kb—体积模量系数;
m—体积模量指数。
邓肯E—B模型切线弹性模量Et和回弹模量Eur的算式与邓肯E—v模型相同。该模型的优点是参数的选取不仅有丰富的经验,而且计算非常简单,可靠性也较高[2]。但由于岩土类材料应力应变关系反应耦合作用,该模型不能反映堆石料的剪缩剪胀性。对于砂、卵石等粗粒岩石材料,该模型还考虑堆石料φ值随围压增大而减小的特性。φ0为当σ3=pa时φ值,对于砂、卵石等Δφ=5°,对于石料Δφ=10°。
(5)
1.3 沈珠江模型
为了较好地反映堆石料实际的变形特性,南京水科院的沈珠江院士吸收邓肯模型和剑桥模型优点,克服非线性弹性模型不能反映堆石料各向异性的缺点,提出了物理概念清楚的双屈服面弹塑性模型[3-4],又称“南水”模型。该模型由椭圆函数和幂函数组成。
(6)
式(6)中:
(7)
(8)
参数r为椭圆的长短轴之比,对于堆石料,一般r取2。
沈珠江模型的两个基本参数分别为切线弹性模量Et和切线体积比μt,其计算式为:
Et=Ei(1-RfSt)2
(9)
(10)
其中,Ei、St分别为初始切线模型和应力水平,其表达式为:
(11)
(12)
式(1)—(12)中:c、φ、Rf、K、n、Cd、nd和Rd均为材料的参数。
2 本构模型在实际坝体计算中的应用
2.1 工程概况
以福建仙游抽水蓄能电站下水库混凝土面板堆石坝为计算实例。该工程正常蓄水位294.0 m,坝顶上游侧设置防浪墙,坝顶高程299.9 m,建基面最低高程224.8 m,最大坝高75.1 m,坝顶宽度考虑施工、交通等要求采用8.0 m,坝顶长263.071 m。上下游坝坡分别采用1:1.405和1:1.35,并在下游坝面高程274.9 m和249.9 m设宽为2 m的马道,坝顶与左右岸公路相接。该坝趾板线两岸地形较平顺,两岸上部为坡残积覆盖,河中为冲洪积覆盖,基岩为辉绿岩,为坚硬岩体,力学强度高。堆石料是面板下游的填筑体,根据其功能和受力情况可以分成若干区域。垫层区及过渡区坡度采用与坝体上游坡同坡度,均为1:1.4,垫层区水平宽度均为3.0 m,过渡区水平宽度均为4.0 m。混凝土面板作为坝体的防渗主体,顶部与防浪墙底连接,厚度为0.3 m,渐变至面板底部厚度为0.5 m。典型断面图见图1。
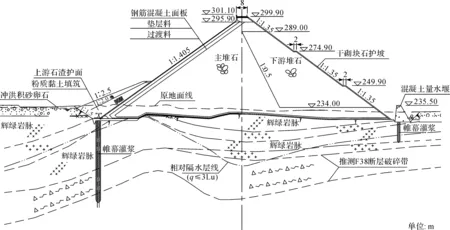
图1 堆石坝典型断面
2.2 计算模型及参数
在三维有限元计算中,将整个坝体分为41个断面,结点总数为8 379,单元总数为7 889(见图2)。对混凝土面板和堆石料单元,均采用六面体八节点或退化的八节点等参数单元模拟。其中,混凝土面板单元442,堆石体6 748,接触面单元442,接缝单元257。坝基面与侧面约束结点为1 036[5]。混凝土面板采用线弹性模型,计算参数见表1。周边缝、面板缝以及面板与垫层之间均采用无厚度的Goodman单元模拟材料边界应力应变的协调关系[6],计算参数见表2。堆石料的本构模型分别采用邓肯E-B模型和沈珠江模型模拟,进而探究堆石料本构模型对面板堆石坝应力变形的影响,以便于对工程数值模拟提供指导。各分区堆石料邓肯E-B模型参数和沈珠江模型中切线体积比参数Cd、nd、Rd取值见表3。

图2 坝体有限元网格划分图
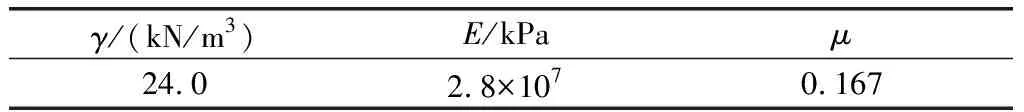
γ/(kN/m3)E/kPaμ24.02.8×1070.167

表2 接触面单元材料参数

表3 堆石料的计算参数
2.3 计算结果与分析
2.3.1 计算结果
采用邓肯E-B模型和沈珠江模型分别对混凝土面板堆石坝蓄水期进行三维有限元计算分析,计算整理所得成果见表4、图3—图6。

表4 坝体及面板应力和位移计算成果

图3 蓄水期河床断面水平位移等值线图
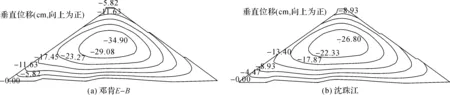
图4 蓄水期河床断面垂直位移等值线图
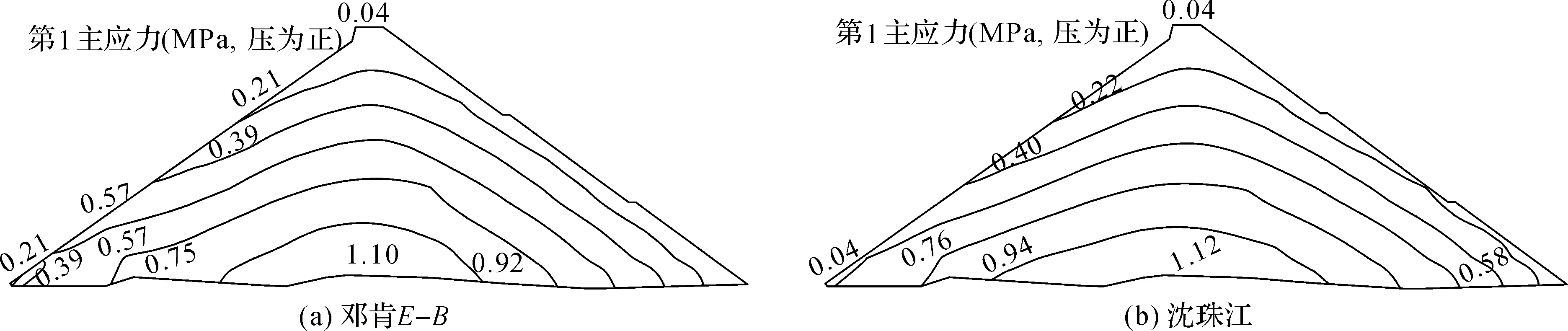
图5 蓄水期河床断面第1主应力等值线图

图6 蓄水期坝体断面第3主应力等值线图
2.3.2 面板应力变形分析
面板应力变形计算成果见表4及图7—图9。
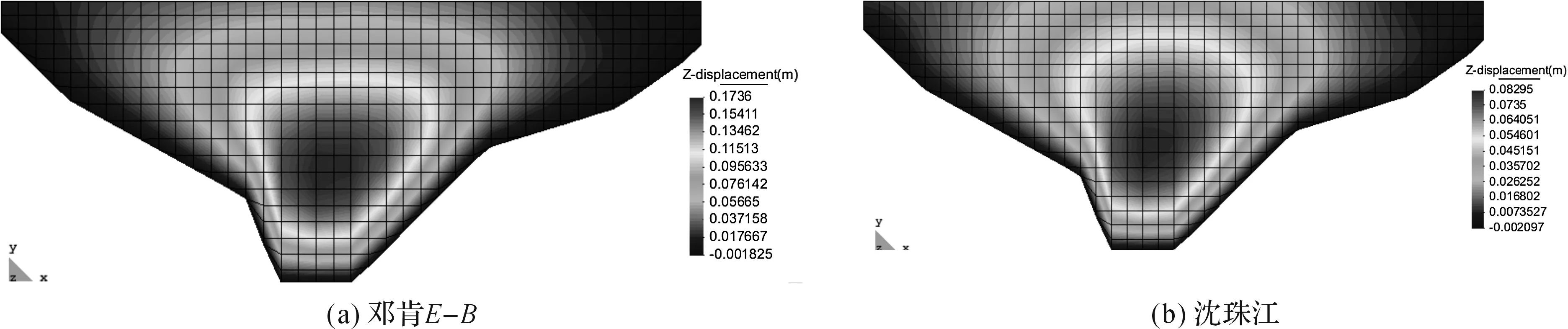
图7 蓄水期面板挠度云图

图8 蓄水期面板坝轴向应力云图

图9 蓄水期面板顺坡向应力云图
规定变形以向下游为正,应力以压为正。
从图7可以看出,混凝土面板在上游水压力的作用下,整个面板变形似锅状,即呈现四周挠度小、中间挠度大的变形规律[8-9]。邓肯E-B模型计算的最大面板挠度为17.4 cm,沈珠江模型计算的最大面板挠度为8.3 cm。邓肯E-B模型比沈珠江模型挠度计算值大得多,计算结果偏安全。
由图8可以看出,整个混凝土面板在坝轴线方向主要处于受压状态。邓肯E-B模型得出蓄水期最大坝轴向压应力为2.28 MPa,压应力不大,从河床段中部往两岸慢慢变小。沈珠江模型计算最大坝轴向压应力为0.63 MPa,比邓肯E-B模型计算值小很多。
从图9可以看出,混凝土面板中部处于受压状态,底板处于受拉状态。这是由于面板在上游水压力作用下产生向下游凹的变形,导致面板中部顺坡向基本处于受压状态,两种模型计算的最大顺坡向压应力分别为3.45 MPa和2.88 MPa。虽然由于面板底部摩擦力的作用使面板底部处于受拉状态,但拉应力不大[10]。
3 结 论
(1)两种模型计算出来的垂直位移规律大致相同,最大垂直位移均在坝体的中间部位。邓肯E-B模型计算出来的结果比沈珠江模型更大,这是因为采用邓肯E-B模型计算时,坝体分层浇筑导致中上部的堆石体应力水平低,弹性模量较小。
(2)蓄水期,邓肯E-B模型计算的河床段面板底板顺坡向拉应力值比沈珠江模型计算值大很多,这与面板堆石坝实际情况不符。此外,邓肯E-B模型计算所得的坝体水平位移与面板挠度也比堆石坝实际值更大,但是作为工程设计的依据是偏安全的,因而具有应用价值。
(3)筑坝材料具有流变性质,两种本构模型均未考虑堆石料的流变性,如何反映材料流变性的本构模型尚需进一步研究。
