临兴区块致密砂岩气储层参数测井精细评价
2022-01-04秦瑞宝李铭宇余杰汤丽娜黄涛李利
秦瑞宝,李铭宇,余杰,汤丽娜,黄涛,李利
(中海油研究总院有限责任公司,北京100028)
0 引 言
致密砂岩气作为中国各类天然气藏的重要组成部分,相对于常规气藏,其物性差,孔隙结构复杂,储层参数难以准确计算[1-2]。为此,国内外学者开展了相应的研究。宋子齐等[3]通过分析岩性、物性、孔隙结构类型与测井响应之间的关系,建立了不同岩石物理相储层孔隙度模型,能够提高致密储层孔隙度计算精度;邵才瑞等[4]利用岩心压汞资料,根据不同毛细管压力曲线形态,按孔隙度范围分类建立J函数与饱和度之间的关系,能够提高低孔隙度低渗透率储层饱和度的计算精度;李霞等[5]基于低孔隙度低渗透率储层孔隙结构特征,提出了双孔隙组分饱和度模型,比较适用于岩电实验中出现“非阿尔奇”现象的低孔隙度低渗透率储层;石玉江等[6]在储层导电机理研究基础上,建立了基于自由水、微孔隙水和黏土束缚水的“三水”并联导电的含水饱和度解释模型,提高了致密储层含气性评价精度。
该文结合临兴区块油藏特点,提出了基于物源分类的岩心标定测井的孔隙度精细评价新方法,建立了基于“非线性阿尔奇”现象的新含气饱和度模型,从而得到精确的孔隙度、饱和度等参数,为增加储量提高产量提供可靠依据。
1 区块概况及储层特征
临兴区块位于鄂尔多斯盆地晋西挠褶带,临近大牛地气田,主要勘探目的层为上古生界二叠系石千峰组、上石盒子组、下石盒子组、山西组、太原组以及石炭系本溪组。
该研究区沉积相类型多样,成岩作用强烈,岩石成分复杂,岩屑、长石含量高。储层主要发育长石岩屑砂岩、岩屑长石砂岩与岩屑砂岩,少量发育岩屑石英砂岩与石英砂岩;成岩相主要分为溶蚀相、绿泥石衬边相、硅质胶结相、碳酸盐胶结相、基质充填相和机械压实相,其中溶蚀相和绿泥石衬边相对储层物性起建设性作用,其他成岩相对储层物性有破坏作用。
该区块储层整体物性较差(见图1),孔隙度为0.3%~21.5%,平均7.3%;渗透率为0.001~89.600 mD(1)非法定计量单位,1 mD=9.87×10-4 μm2,下同,平均0.330 mD,其中致密和低渗透砂岩储层占比近80%。
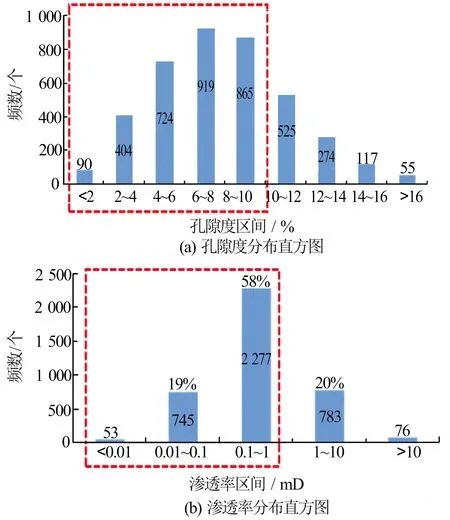
图1 临兴区块储层岩心分析孔隙度、渗透率分布情况
2 储层参数测井精细评价
孔隙度和饱和度是储量评价中最重要的2个参数。但由于研究区含气层位多、沉积相类型多样、岩石成分复杂、成岩作用强烈,给准确求取孔隙度和饱和度带来挑战。为提高储层参数计算精确度,满足储量估算要求,开展了孔隙度、饱和度精细评价研究。
2.1 基于物源分类的岩心标定测井孔隙度计算方法
临兴区块岩石成分复杂,导致岩石骨架参数多变,采用常规三孔隙度测井评价方法结合岩心数据进行建模,发现密度与岩心分析孔隙度的相关性要明显好于中子和声波时差与岩心分析孔隙度的相关性,因此,采用单密度测井资料计算孔隙度。但由于研究区含气层位多,在平面和纵向上分布不均,不同井、不同层位的含气性变化大,含气性和岩性的变化对密度测井响应存在较大影响。上石盒子组岩心分析孔隙度与测井密度相关系数仅为0.73,这样的相关性对于中高孔隙度渗透率储层基本满足计算精度要求,但对于特低孔隙度渗透率和致密储层来说则不够。利用回归公式计算的孔隙度与岩心分析孔隙度相对误差高达20%以上,无法满足储量估算的精度要求。该文结合区块沉积物源和沉积相分析,在综合考虑含气性变化的前提下,建立岩心标定测井孔隙度精细评价模型,有效解决孔隙度计算精度不高的问题。
诸多研究成果表明,鄂尔多斯盆地北部上石炭统中二叠统砂岩的物源区主要为再旋回造山带物源区,可划分出乌海-银川、杭锦旗-东胜及准格尔旗-府谷等3个物源区。受物源分类的影响(不同物源控制岩屑含量的多少),盆地内部石英砂岩分布以杭锦旗-东胜为界,具有明显东西分区性,主要分布于盆地西部,越往东石英含量逐渐降低,而岩屑含量则逐渐增高,盆地东部总体上是岩屑砂岩的覆盖区[7-8]。结合临兴区块X射线衍射分析资料统计上石盒子组东西区岩石成分分布情况(见表1),可以看出,从西往东,石英含量降低,长石和岩屑含量增加,并且图2中薄片分析表明,位于东边的LX-A井其岩屑含量明显多于西边的LX-B井,整体上与鄂尔多斯盆地大趋势保持一致。因此,临兴区块平面上岩石骨架密度应该表现为西低东高的特征。

表1 临兴区块上石盒子组岩石成分统计表
从区域沉积背景分析,临兴区块主要目的层上古生界沉积环境经历了太原组滨浅海相潮坪障壁潟湖沉积,到山西组海陆过渡相曲流河三角洲沉积,再到下石盒子组、上石盒子组及石千峰组河流三角洲发育的内陆湖盆陆源碎屑沉积的发展演变,下部海相、海陆过渡相易形成灰质胶结,碳酸盐岩含量高,岩石骨架密度增大。利用X射线衍射分析资料统计分析临兴区块不同层位碳酸盐岩含量的分布情况(见表2),总体上看,从下而上自太原组到石千峰组,碳酸盐岩含量逐渐降低,与区域沉积相认识相符,故纵向上岩石骨架密度表现为上低下高的特征。
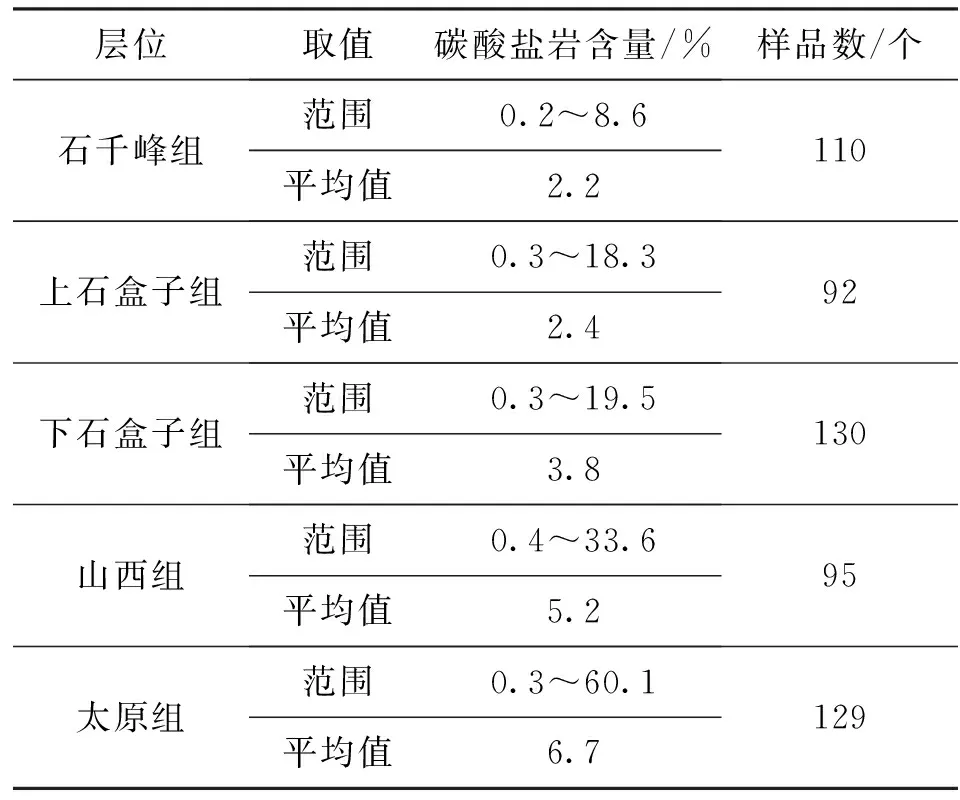
表2 临兴区块碳酸盐岩含量统计表
结合岩心分析孔隙度,利用密度测井孔隙度计算公式,分区、分层位标定砂岩骨架密度值,具体标定结果见表3。

表3 临兴区块岩石骨架密度取值表(单位:g·cm-3)
研究区致密砂岩气储层密度孔隙度与中子孔隙度的差值大小能够反映储层含气性[9],含气性越好,密度孔隙度与中子孔隙度差值也会越大。自然高产气层测井响应特征表现为自然伽马值小于50 API、密度中子孔隙度曲线表现为明显的正差异,密度孔隙度与中子孔隙度差值大于或等于4%。因此,可以根据流体性质对测井响应的影响程度确定地层流体密度值。
该文据此开展临兴区块孔隙度计算,以使计算精度达到储量规范的要求。
(1)
φt=φe+Vshφsh
(2)
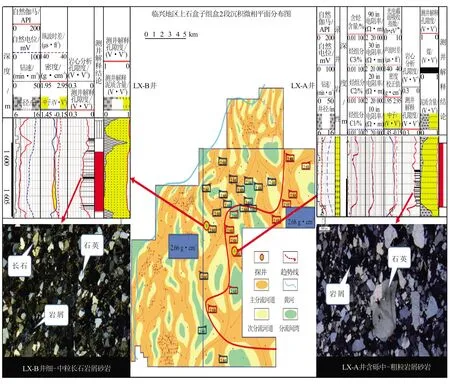
图2 临兴区块上石盒子组岩石骨架密度值分布*非法定计量单位,1 ft=12 in=0.304 8 m; 1 b/eV=6.241 46×10-10 m2/J,下同
式中,φe为有效孔隙度,小数;φt为总孔隙度,小数;ρlog为体积密度测井值,g/cm3;ρma为砂岩骨架密度,g/cm3;ρsh为泥岩密度值,取2.62 g/cm3;Vsh为泥质含量,小数;φsh为泥岩孔隙度,取0.10 g/cm3。ρfl为地层流体密度,当密度孔隙度减中子孔隙度差大于或等于4%时,取0.80 g/cm3,否则取1.00 g/cm3。以临兴区块上石盒子组岩石骨架密度标定结果为例(见图2中盒2段沉积微相平面分布图),以图2中红线为界,西边岩石骨架密度取2.66 g/cm3,测井计算孔隙度与岩心分析孔隙度吻合最好(见图2中LX-B井处理成果图),东边岩石骨架密度取2.68 g/cm3,测井计算孔隙度与岩心分析孔隙度吻合最好(见图2中LX-A井处理成果图),其他层段岩石骨架密度取值见表3。最终形成了平面上东、西分区,纵向上分层位的砂岩骨架密度取值规律,总体上骨架密度呈现西低东高,上低下高的趋势,与区域物源分类和沉积背景相一致。
2.2 基于“非阿尔奇”现象的含气饱和度新模型
致密砂岩储层孔隙结构复杂、岩电关系复杂,岩电参数难以准确求取,传统阿尔奇或印度尼西亚公式评价含水饱和度不能满足储量估算的精度要求。该文基于临兴区块大量的岩电实验数据,针对致密砂岩储层分析不同孔隙类型储层的岩电关系,构建新的致密砂岩储层含气饱和度定量评价模型。
2.2.1岩电关系分析
根据Rasmus多重孔隙介质电阻率模型[10],认为岩石孔隙结构对岩石电学性质有控制作用。图3为临兴区块铸体薄片资料显示的4种孔隙类型及实验分析得到的岩电关系,储层孔隙结构可分为粒间孔隙型、粒间-溶蚀孔隙型、泥粉-粒间孔隙型和粒间-裂缝孔隙型,岩电实验数据显示的复杂孔隙类型是导致数据点分区分散、岩电关系产生差异的原因。分析不同孔隙类型的胶结指数m与孔隙度的关系发现:溶蚀孔隙的存在将使胶结指数m增大,基质孔隙度愈小、溶蚀孔隙度愈大,m值愈大;微裂缝发育可降低胶结指数m值,基质孔隙度愈低、裂缝孔隙度愈大,m愈小;在相同孔隙度下,粒间-裂缝孔隙型胶结指数m最小,粒间-溶蚀孔隙型胶结指数m最大。4种不同孔隙类型储层岩石电阻率指数与含水饱和度的关系整体呈现指数关系,粒间孔隙、粒间-溶蚀孔隙、泥粉-粒间孔隙和粒间裂缝孔隙的饱和度指数n依次增大。

图3 临兴区块薄片分析孔隙类型和岩电关系
2.2.2新饱和度模型及参数确定方法
(1)胶结指数m值的确定
地层因素与岩心分析孔隙度的关系表明,临兴地区胶结指数m是一个变值,m值与孔隙度呈近似单调递增关系。但不同层位的变化趋势不尽相同,若不分层拟合相关系数仅为0.417,无法满足计算精度要求。故分层位建立m值的确定方法(见图4)。图4为不同层位胶结指数m与孔隙度的关系,分层拟合的公式精度明显提高。由于石千峰组和山西组m值变化较小,可以选取固定的m值。
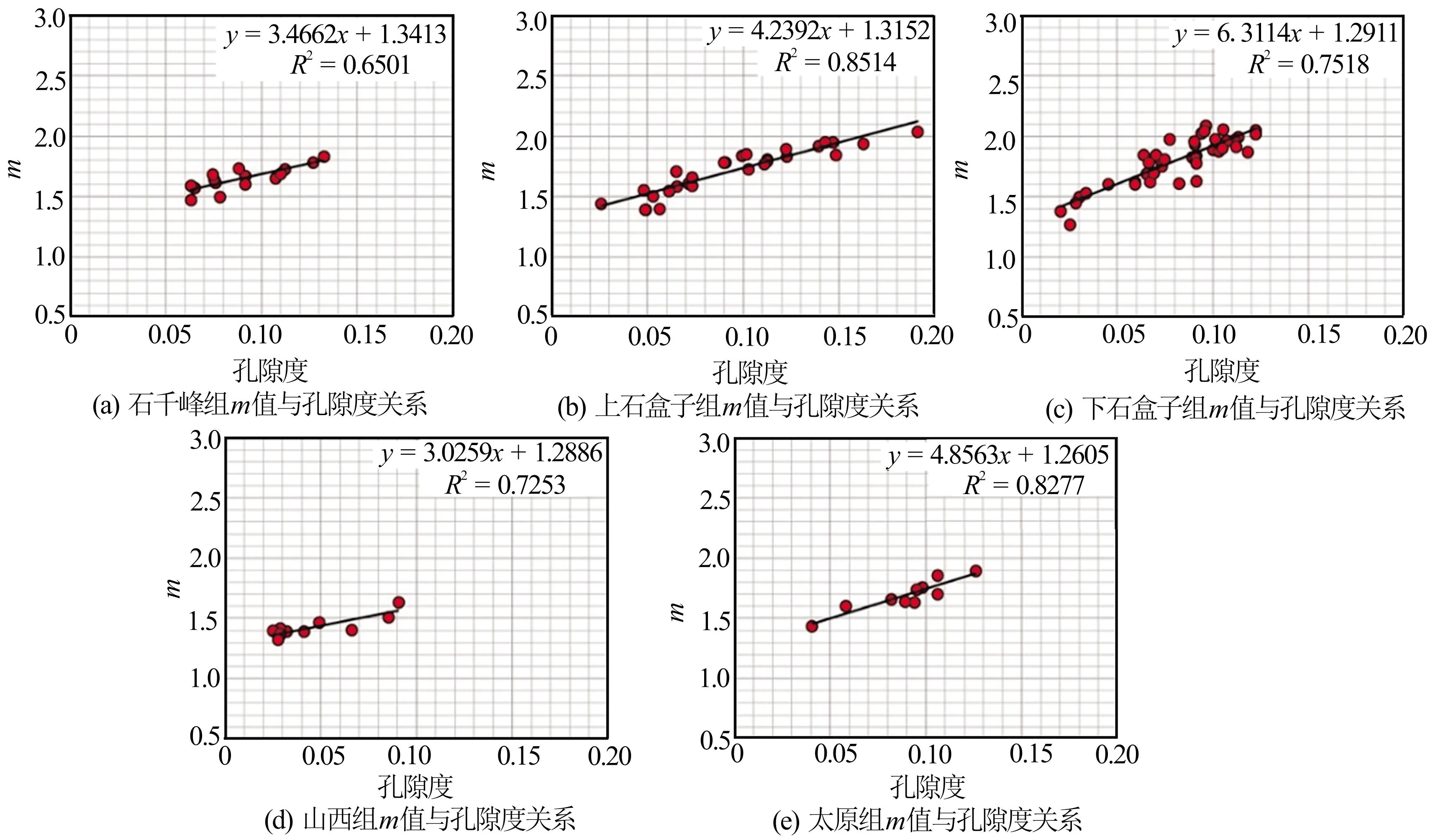
图4 临兴区块不同层位胶结指数m值与岩心分析孔隙度的关系
(2)新饱和度系数xb和电阻率指数xn值的确定
研究区岩电实验结果表明,岩石电阻率指数与含水饱和度在双对数坐标系下呈现较明显的非线性相关性。为了进一步提高饱和度评价精度,将岩电实验数据分为2类,建立电阻率指数与含水饱和度的指数关系[见图5(a)],分别得到饱和度系数。Ⅰ类以泥粉粒间孔隙、粒间裂缝孔隙和小孔隙为主,Ⅱ类岩样以粒间孔隙、粒间溶蚀孔隙和大孔隙为主,Ⅰ类饱和度系数n值大于Ⅱ类饱和度系数n值。
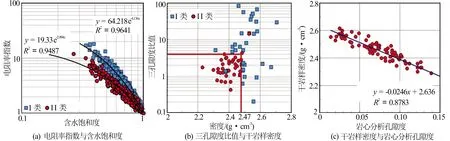
图5 临兴区块2类储层测井定量区分图版
但是,对于这2类储层能否利用测井资料区分开来,是新模型得以在实际测井资料处理中应用的关键。相比于Ⅰ类储层,Ⅱ类孔隙结构构成的储层物性更好,储集渗透能力强,含气性更好,基于中子、密度、声波三孔隙度测井与储层含气性的密切关系,提出利用三孔隙度比值B放大储层含气信息从而识别不同类型储层。经过多种参数交会图分析,发现测井三孔隙度比值B与干岩样密度DENG交会图能够区分2类储层[见图5(b)],Ⅰ类储层:B>4,DENG>2.47 g/cm3;Ⅱ类储层:B≤4,DENG≤2.47 g/cm3。
其中,三孔隙度比值计算公式为
(3)
式中,B为三孔隙度比值,无量纲;φs为声波孔隙度,小数;φN为中子孔隙度,小数;φd为密度孔隙度,小数。
干岩样密度可以通过建立与岩心分析孔隙度的相关关系(见图5(c))计算得到
DENG=-0.0246φ+2.636
(4)
式中,DENG为干岩样密度,g/cm3;φ为岩心分析孔隙度,小数。
在上述岩电关系的基础上,建立新的岩电关系
(5)
(6)
联合式(5)和式(6),可得饱和度模型的关系式
(7)
式中,F为地层因素,无量纲;I为电阻率指数,无量纲;Ro为100%含水岩石电阻率,Ω·m;Rw为地层水电阻率,Ω·m;Rt为地层电阻率,Ω·m;φe为有效孔隙度,小数;m为孔隙胶结指数;α为岩性系数,取值1;xb和xn为新饱和度模型系数,区别于阿尔奇公式中的b和n值。最终分层位确定了不同类型储层新饱和度模型的参数取值(见表4)。

表4 新饱和度模型参数取值表
3 测井资料处理及精度分析
依据上述储层参数精细评价方法对50口取心井开展实际测井资料的处理,利用270层的岩心分析孔隙度对测井解释孔隙度进行验证,相对误差均小于8%[见图6(a)],满足储量估算的精度要求。另外,由于密闭取心对钻井工艺要求极高、成本昂贵,研究区仅对少量井进行了密闭取心。研究表明,蜡封岩心分析含水饱和度及3 MPa高压半渗透隔板束缚水饱和度数据可用于测井计算饱和度的检验[11]。最终利用研究区3口井8个小层密闭取心、24口井61个小层蜡封岩心、8口井23个小层半渗透隔板的饱和度数据对测井计算饱和度进行检验[见图6(b)],其绝对误差均小于5%,满足储量估算的精度要求。
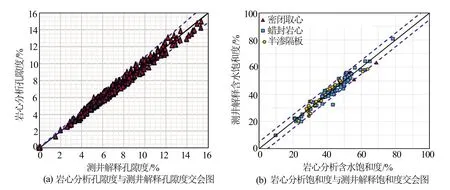
图6 临兴区块测井解释孔隙度和含水饱和度计算精度分析
图7为利用新模型对LX-C井储层参数精细处理的结果。从左到右第7道蓝色曲线为原解释孔隙度曲线,红色曲线为新方法解释孔隙度曲线,第8道蓝色曲线为原解释含水饱和度,红色曲线为新方法解释含水饱和度,黑色杆状线为岩心分析孔隙度、饱和度数据。新模型计算结果与岩心分析数据吻合更好,且孔隙度和含气饱和度均高于常规解释结果。通过统计,图7中3套气层新方法处理的平均孔隙度为8.3%,平均含气饱和度为72.5%;常规解释的平均孔隙度为6.1%,平均含气饱和度为57.2%。分别高出2.2%和15.3%。仅此3个气层而言,其他储量计算参数保持不变,采用该研究提出的精细评价方法处理后,计算储量将提高9.6%。
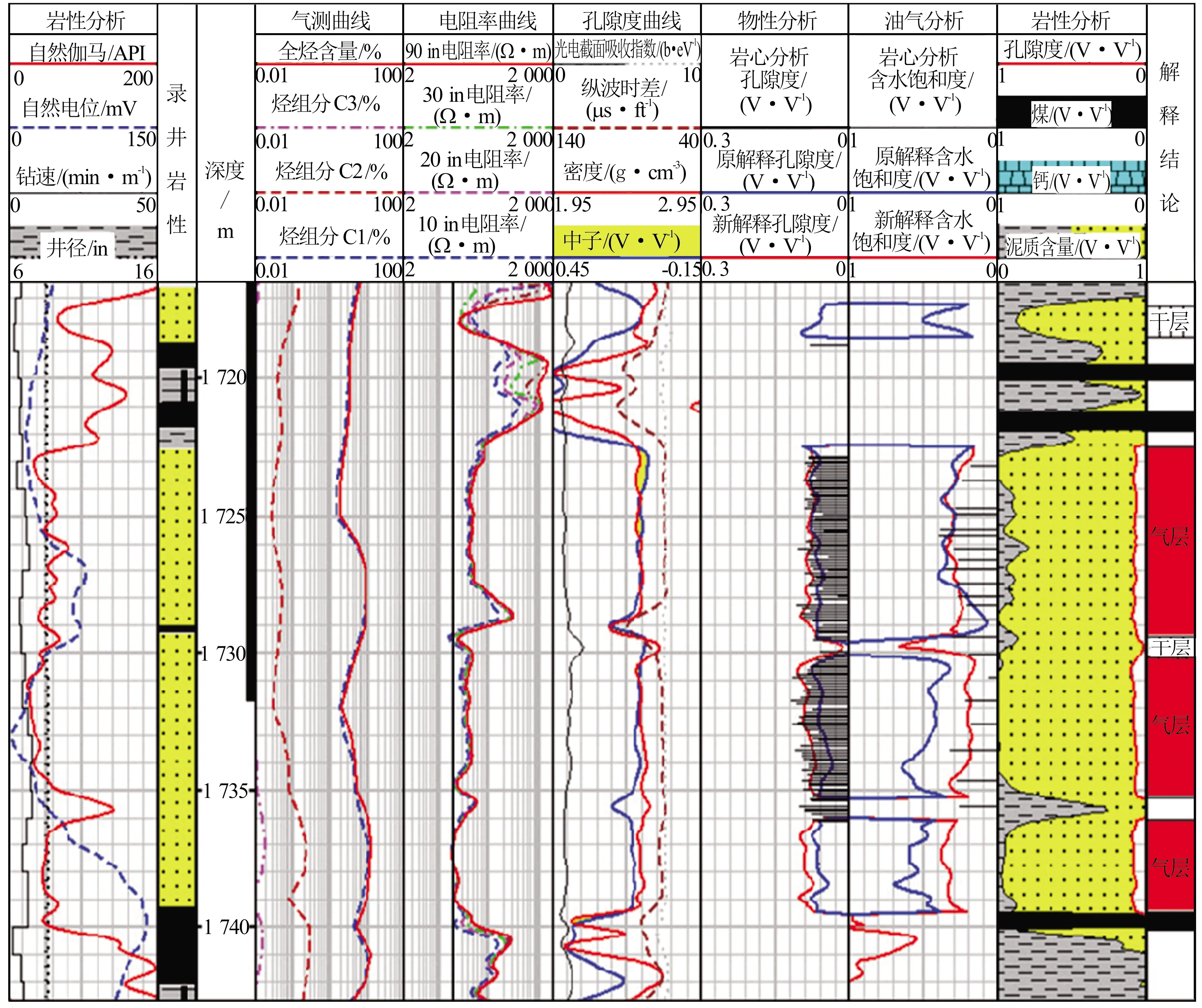
图7 LX-C井新老方法处理结果对比
4 结 论
(1)以大量岩心分析资料为基础,以岩心标定测井的方法,建立了基于物源分类的孔隙度计算方法,解决了临兴区块岩石成分复杂、岩石骨架参数变化大导致的孔隙度计算精度低的问题。研究结果表明,由于岩屑和碳酸盐岩含量高,导致骨架密度值明显大于砂岩理论密度值(2.65 g/cm3)。该方法对类似取心资料少或勘探新区的孔隙度的精确计算,具有一定的指导意义。
(2)临兴区块储层孔隙类型多样,导致岩电关系复杂,使得传统的含水饱和度模型计算精度低。通过对大量的岩电实验数据进行分析,认为在双对数坐标系下,岩石的电阻率指数与含水饱和度呈现为非线性,分2类储层建立了新含气饱和度模型。通过密闭取心、蜡封岩心和半渗透隔板岩心分析数据验证,新模型计算的饱和度绝对误差小于5%,满足了储量规范要求。
(3)该研究成果为临兴区块提供了精确的孔隙度、饱和度参数,为致密砂岩气层分类、压裂改造奠定了坚实基础,为增储上产提供了重要的技术支撑。
猜你喜欢
——以鄂东临兴神府地区为例
