基于雷达组合反射率拼图和深度学习的中尺度对流系统识别、追踪与分类方法*

南刚强 陈明轩 秦 睿 韩 雷 曹伟华

1.中国海洋大学，青岛，266100 2.北京城市气象研究院，北京，100089

1 引言

中尺度对流系统（Mesoscale Convective System，MCS）是具有旺盛对流性运动的天气系统，其水平尺度大约为10—2000 km，生命期在3 h以上。Schumacher等（2006）研究了美国地区1999—2003年的极端降水事件，发现所有事件中有66%和暖季事件中有74%与MCS有关，并且美国北部几乎所有的极端降雨事件都是由MCS引起的。Schumacher等（2020）研究表明MCS会产生很大比例的暖季降雨，且在气候变暖的情况下，MCS的频率和强度也可能会增大。中国国家气候中心分析结果显示，于1954、1969、1980、1991、1996、1998、1999、2003和2007年发生的特大暴雨洪涝都与MCS存在直接的关联，这些灾害给国民经济和人民生命财产安全造成了重大损失（王晓芳等，2011）。自2012年以来，华北中东部暴雨事件频发（雷蕾等，2020），对社会造成了巨大损失，并且这些暴雨特别是短时强降水的形成均与MCS存在直接关系。因此，做好MCS及其致灾天气的预报、预警，对人们了解暴雨、龙卷风和山洪等气象灾害的发展及演化有很大的帮助。

资料的选择对MCS的研究有着至关重要的影响。从中尺度天气的角度判断，MCS的尺度范围相对较大，且空间变化较广，形态较为复杂，因此近几十年来，气象学家通常使用较大范围的卫星或雷达组网数据进行MCS的监测、识别、追踪和预报（Houze，2018）。

基于雷达探测资料的常用识别MCS的方法有2类。一类是基于雷达拼图资料的TITAN算法（Thunderstorm Identification，Tracking，Analysis and Nowcasting）（Dixon，et al，1993）。TITAN属于对流风暴三维特征自动识别、跟踪、分析算法的典型代表，后续经过了多次改进和完善，并在多个临近预报系统中得到应用（Mueller，et al，2003；韩雷等，2007；Han，et al，2009；陈明轩等，2006，2010）。另一类是基于雷达拼图资料开发的SCIT算法（Storm Cell Identification and Tracking Algorithm）（Johnson，et al，1998），并 借 助Davis等（2006a，2006b）开发的模式评估工具（MODE，Method for Objective-based Diagnostic Evaluation）进 行 识别。但TITAN和SCIT均属于风暴“质心”识别和追踪算法，对尺度较小的超级单体风暴或孤立的风暴单体的识别效果更好，而对于结构和形态较为复杂的MCS的识别有时不够准确。人们为了能够利用SCIT准确地识别MCS，对SCIT算法进行了一定改进，将SCIT算法中识别的位置比较接近的风暴单体组成MCS，以便对MCS进行跟踪和预报。随着机器学习算法的广泛应用，人们开始借助人工智能来实现MCS的自动识别，Haberlie等（2018a）使用随机森林、梯度提升和极度梯度提升3种分类算法实现了美国MCS的自动识别。

MCS的移动轨迹追踪通常也使用TITAN算法或改进的SCIT算法实现，但是这类风暴“质心”算法也存在与上述识别MCS类似的追踪缺陷。另一种常见的MCS移动轨迹追踪方法是基于雷达回波的交叉相关追踪（Tracking Radar Echoes by Crosscorrelation，TREC）（Rinehart，et al，1978），该方法同样适用于基于卫星观测资料的MCS追踪。杨吉等（2015）利用TREC和面积重叠算法实现了新的MCS追踪预报方法。最近，曹伟华等（2019）将TITAN算法和TREC算法进行融合，发挥不同识别追踪算法的优势，以提升强对流系统的识别和临近预报水平。但是，TREC算法最大的问题是交叉相关矩阵的计算设置与对流系统回波的尺度密切相关，使得不同尺度对流系统的追踪效果和精度差异较大。对于MCS的追踪，还有Skok等（2009）提出的时间空间目标建立法，但是，该方法有一个很大的弊端，对多个对象的合并（分裂）将导致一个单一的、过度扩展的风暴带。作为一种替代方法，可以使用Lakshmanan等（2009）提出的时、空重叠追踪法，该方法将时、空对象构建过程仅应用于两个相邻时次雷达图像在空间上重叠的风暴。

准线性MCS包含一条对流线，也就是一个连续或接近连续的对流回波链，该回波链共享一个几乎共同的前缘，并以近似串联的方式移动，包括其按照一个接近直线或中等弯曲的弧线方式排列（Parker，et al，2000）。准线性MCS（如飑线）的分类是研究MCS的一个重要课题，尤其对短时强降水和暴雨特征的研究有重要意义。Parker等(2000）使用2 km分辨率的美国雷达组合反射率因子数据，研究了MCS的主要组织形态，根据对流线和层状云的相对位置将准线性MCS分为尾随层云（Trailing Stratiform，TS）、前 导 层 云（Leading Stratiform，LS）和 平 行 层 云（Parallel Stratiform，PS）3类，并研究了每种类型的基本特征，形成了经典的线状MCS分类概念模型。Wang等（2014）借鉴上述工作，利用2010年6—7月长江流域的雷达拼图和观测资料，分析了长江中下游地区梅雨季MCS的类型和特征。Ashley等（2019）使用图像分类和机器学习方法对22 a的美国地区雷达拼图数据进行分割、分类和准线性对流系统（Quasi-Linear Convective Systems，QLCS）追踪，该研究更进一步地说明了自动风暴形态分类的实用性，减少了研究人员手动形态学分类的耗时和时空限制。Jergensen等（2020）使用机器学习并基于雷达探测数据和邻近探空资料，将雷暴有效地分为3类：超级单体、QLCS和无组织对流。

MCS的自动识别、跟踪和分类本身就是一个复杂的工作，涉及到很多核心技术与算法。鉴于此，文中结合机器学习算法来实现MCS的自动识别，将MCS的识别转化为从特定MCS切片中抽取到的样本的预测问题。并且，基于追踪得到的运动轨迹和准线性MCS中TS、LS和PS三种类型的组织结构，提出了新的分类算法，也就是根据MCS运动方向与层状云和强对流云区域在识别的MCS切片中的分布特征，实现对准线性MCS的分类。

文中首先通过分割雷达拼图数据和抽取MCS切片中的特征将MCS的识别转换为二分类问题，并使用机器学习算法训练数据集得到最优分类器进而实现MCS的自动识别。再对机器学习模型识别的MCS进行追踪，得到包含MCS信息的数据集和追踪轨迹。最后根据轨迹矢量与MCS切片拟合椭圆短轴的夹角以及拟合椭圆长轴两侧的层状云和强对流云面积之比，建立准线性MCS的分类算法。

2 模 型

2.1 深度学习简介

深度学习是机器学习的一个重要分支，它能自动地从输入数据中抽取更加复杂的特征，使网络模型的权重学习变得更加简单有效。早期的深度学习受到了神经学的启发，使得深度学习可以胜任很多人工智能的任务，到如今，深度学习已经从最初的图像识别领域扩大到了机器学习的各个领域。

文中使用深度学习中的深度神经网络（Deep Neural Networks，DNN）进行MCS的特征识别，并将其训练所得模型的预测结果与传统的机器学习算法做对比。由于用到的其他3种普通机器学习分类算法（支持向量机（SVM）、随机森林（RF）、极度梯度提升决策树（XGBoost））都是基于开源的Scikit-Learn库（Pedregosa，et al，2011）实现的，在此不予介绍，读者可参考相关文献。下文将主要介绍DNN模型的实现。

2.2 深度神经网络（DNN）模型

2.2.1 网络结构

文中使用的DNN模型（Bengio，2009）是一个4层的全连接神经网络结构，包含2个不同节点的隐藏层，第1层为输入层，节点数为MCS样本的特征数量（共14个，后面会详细介绍这些特征的定义）；第4层为输出层，含有2个节点，分别对应预测结果MCS（标记为1）和non-MCS（非MCS，标记为0）。

DNN模型的主要参数见表1。表中的GradientDescent即梯度下降法，是一种常用的优化器；Relu是激活函数，表达式见式（1），Relu函数在正区间内的斜率为常数，避免了模型训练过程中梯度消失的情况，并且在梯度下降过程中使得模型能够快速收敛。

表1 DNN模型主要参数Table 1 Main parameters of the DNN model

2.2.2 学习率和损失函数设置

在训练神经网络时，需要设置学习率来控制网络参数更新速度，学习率决定了网络参数每次更新的幅度。学习率太小，会导致模型收敛过于缓慢，进而增加训练的时间成本，有时甚至导致模型出现“无学习能力”的情况；学习率太大，使得模型无法靠近或达到最优解，最终导致模型无法收敛。为了解决此问题，使用指数衰减法来控制学习率的变化，使模型趋于最优解。

式中，lr是学习率；lr_base是初始学习率；α是小于1的衰减率，在本试验中取0.99；decay_step是常数，表示衰减速度；train_step是训练轮次。

损失函数是模型优化的对象，通过最小化损失函数使模型达到收敛状态，减少模型预测值的误差。本试验解决的是二分类问题，所以用交叉熵作为该模型的损失函数。交叉熵用来刻画两个概率分布的距离，对于两个特定的概率分布p和q，交叉熵的计算方法为

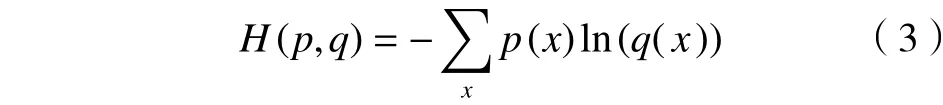
在本试验中，p表示样本的标签，q表示网络输出结果的概率分布。

根据本研究的需要，为了将神经网络的输出结果转化为概率分布，用Softmax回归作为网络输出层的额外处理层。假设原始网络的输出为yi(i=1,2,···,n)，则经过Softmax回归处理后的结果为

2.2.3 过拟合问题

在神经网络的训练过程中，模型经常会出现过拟合的情况，也就是模型在训练集上的拟合效果很好，但在测试集上的预测值和真实值差异却很大。为了解决训练得到的模型出现过拟合问题，通常会在损失函数中引入正则化。正则化就是在损失函数中加入刻画模型复杂度的指标来限制权重的大小，进而减小训练数据中的随机噪声对模型拟合的影响。常用的有L1正则化和L2正则化

式中，w表示网络的权重，模型的参数复杂度由网络的所有权重系数（w）决定。L1正则化更趋向于产生一个稀疏模型，而L2正则化可以更好地防止模型过拟合，故本试验使用L2正则化。假设模型的损失函数为L（θ），正则化系数为λ，则引入L2正则化后的优化函数如下

此时，在优化模型时会直接优化Loss函数，而不是损失函数L（θ）。需要特别说明的是，本试验为了增加DNN模型在测试集上的健壮性（即模型稳定高效且性能优越），引入了滑动平均模型。在采用梯度下降法训练神经网络时，使用滑动平均模型在很多应用中都可以一定程度上提高最终模型在测试数据上的性能。简单来说，就是数据每次训练得到的模型都受到之前模型的影响，进而影响后面模型的训练，这个影响随着训练次数的增加而减小，这样可以让模型的训练更加趋于稳定。

3 试验设计

3.1 试验数据及预处理

文中所用的雷达拼图数据的格点分辨率为1 km×1 km，覆盖整个京津冀地区，区域大小为800 km×800 km，时间间隔为6 min。该数据具有高时、空分辨率特征，并且覆盖范围较广，非常适合于京津冀地区MCS的识别与追踪。该雷达拼图数据是北京自动临近预报系统（BJ-ANC）的产品（陈明轩等，2010），BJ-ANC系统在形成上述雷达拼图资料过程中对京津冀地区每部雷达基数据均进行了较为严格的质量控制，包括地物杂波、超折射回波、0℃层亮带回波的自动识别和剔除（陈明轩等，2010），这里不再赘述。

京津冀地区原始雷达拼图数据的投影坐标为非等间隔经纬度投影，为了方便后面试验的进行，需要对每个网格的经度和纬度等间隔化。经处理后每个网格在地理上的大小近似为1 km2，数据的经纬度范围（36.21°—43.40°N，112.03°—120.90°E）。这样处理只是细微地改变了每个网格点的经纬度，每个网格的值依旧保持不变。因为夏季是京津冀地区MCS的高发季节，并且要得到足够多的样本来训练模型，故选择2010—2019年中5—9月的数据进行试验，其中2010和2014年缺失5月的数据。

3.2 数据分割及MCS切片提取规则

为了用机器学习模型识别雷达拼图中的MCS，首先需要分割雷达拼图数据得到候选MCS切片，进而抽取样本特征。这里的MCS切片，是指通过搜索满足特定阈值大小和强度标准的雷达回波图像中的相连通像素组，而组合得到的雷达探测强对流区域，用该MCS切片表示单个时刻MCS的空间强度和形态特征。在本研究中，参考Parker等（2000）的工作（简称PJ00标准），PJ00标准将MCS定义为一个至少持续3 h且包含连续或半连续深湿对流的降水区域，该降水区域的长轴不小于100 km。根据PJ00标准，分割雷达拼图数据中MCS切片的阈值如表2所示，其中对流区域搜索半径和层状云区域搜索半径并不是唯一的，对流区域搜索半径的常用取值有6、12、24和96 km，而层状云区域搜索半径的常用取值有48、96和102 km。根据Haberlie等（2018b）关于美国中纬度地区MCS追踪的研究，对流区域搜索半径取24 km、层状云区域搜索半径取96 km时，追踪效果最好。所以本试验这两个指标也分别设为24和96 km进行雷达拼图数据的分割及MCS的追踪。

表2 用于分割雷达拼图中MCS的指标阈值Table 2 Various thresholds used to segment MCS in radar mosaic data

以图1所示原始雷达拼图数据为例，分割过程可以总结为以下3个步骤：（1）确定至少包含一个强对流回波（≥50 dBz）像素的对流回波（≥40 dBz）区域，并将面积大于40 km2的对流区域选定，如图2a中黑色实线标记的区域；（2）如果选定的对流区域的距离在指定半径24 km内，则将它们连接，若连接后区域的最佳拟合椭圆的主轴长度（即MCS核长度）至少为100 km，则将其视为候选MCS核，如图2b黑色实线区域；（3）将指定半径96 km内的层状云回波（≥20 dBz）区域与其各自的候选MCS核相关联，并用黑色轮廓线勾勒出最终的候选MCS切片，如图2c所示。

图1 原始雷达拼图数据（2014年6月17日11时59分36秒（世界时，下同））Fig.1 Original radar mosaic data （11：59：36 UTC 17 June 2014）

图2 使用雷达拼图数据 （2014年6月17日 11时59分36 秒） 演示候选MCS切片的分割过程（a.包含强对流单元且面积大于40 km2的对流区域；b.连接指定半径24 km内的对流区域，将主轴长度超过100 km的连接区域确认为MCS核；c.关联MCS核指定半径96 km内的层云区域得到候选MCS切片）Fig.2 Demonstration of segmentation steps for candidate MCS slices using radar mosaic data （11：59：36 UTC 17 June 2014）（a.convection areas greater than 40 km2 with intense convection；b.connected convection area within a specified radius （24 km），and the connected area is considered to be the MCS core if its major axis length is at least 100 km；c.candidate MCS slice is identified by connecting the strtatiform pixels that are within the specified radius （96 km） of MCS core）

3.3 MCS特征化及识别

为了实现文中的MCS分类目标，必须将MCS切片信息具体特征化从而得到训练样本。每个MCS特征的选择是参考先前的相关研究而确定的（Haberlie，et al，2018a），并使用Scikit-Image（van der Walt，et al，2014）中的图像处理函数来完成特征值计算。共选取14个MCS特征，可以简单将其分为面积特征、比值特征、几何特征和统计特征，具体参见表3。

表3 MCS样本特征列表Table 3 Sample features of MCS

由于每个网格的面积是1 km2，因而面积特征大小即为满足阈值的网格数。14个MCS特征的计算都比较简单，含义也很明确，此处对较复杂的几何特征做一些简单说明。几何特征主要涉及到MCS拟合椭圆和凸包两大形态，对应的相关特征就是拟合椭圆的长轴、短轴和离心率以及凸包区域的面积。凸包（图3a）是将不规则图形的最外层点连接起来而得到的凸多边形，即该不规则图形的最小外接凸多边形。拟合椭圆是指与不规则图形区域具有相同标准二阶中心矩的椭圆（图3b），即最佳拟合椭圆。离心率是该椭圆的焦距与长轴之比，用来衡量椭圆的扁平程度，取值范围为（0，1），离心率越大椭圆越扁平。

图3 MCS切片的凸包 （a） 和拟合椭圆 （b） 示意Fig.3 Convex hull （a） and fitting ellipse （b） of MCS slice

抽取完每个候选MCS切片的14个特征后，为每个样本主观分配MCS和non-MCS标签，将其制作成含有大量样本的数据集，并将数据集按照年份划分为训练集和测试集，具体见表4。数据集的划分遵循以下2个原则：（1）训练集和测试集的比例要适当，既要保证足够多的样本来训练模型，也要有充足的测试集来评估模型的性能，通常按照7∶3的比例划分训练集和测试集；（2）要保证训练集中正、负样本的平衡性。训练集用来训练分类器得到最优的机器学习模型，而测试集则用作独立数据来评估模型的分类性能，根据最优模型来识别候选MCS切片是否为真实的MCS。如前所述，文中用4种常见的机器学习算法作为试验的分类器，分别是RF、SVM、XGBoost和DNN，前3种算法都是基于Scikit-Learn库实现，属于传统机器学习算法，对解决二分类问题有很好效果。DNN模型是基于Tensorflow框架搭建的全连接层神经网络，该模型的可调控参数较多，优化器和损失函数的选择较为灵活，并且可以调用GPU加速模型的训练速度，都极大提高了模型的潜力和应用空间。

表4 不同类别和年份的训练集和测试集样本数Table 4 Training and testing counts by classification and year

3.4 MCS追踪

根据PJ00标准，从对流系统的结构规模来看，由对流单体或者对流簇形成的MCS及其伴随的中尺度环流必须持续足够长的时间。鉴于此准则，对雷达拼图中的MCS进行追踪，必须满足如下条件：（1）尺度和强度要求的分块必须在时间序列上进行时、空关联；（2）该关联必须至少持续3 h以上。追踪的目的是在时间和空间上关联机器学习模型识别出的MCS切片，以生成包含强度、空间和时间信息的MCS条带数据集，并根据追踪轨迹实现准线性MCS中TS、LS和PS三种模型的特征分类。

本试验使用时空重叠追踪法（Lakshmanan，et al，2009）进行MCS追踪，该方法对两个相邻时次雷达拼图在空间上相重叠的风暴进行匹配。对于2018和2019年5—9月的所有时间间隔为6 min的测试集雷达数据，根据DNN模型识别MCS的评估结果确定分类阈值为0.5，依此阈值来选择当前时刻和下一时刻的MCS切片。匹配过程中将建立一个二维矩阵，“矩阵行”表示在现有追踪轨迹内的一个当前时刻MCS切片，“矩阵列”表示下一时刻未经匹配的MCS切片。分别计算前、后2个时刻重叠的MCS切片的相似度，根据最小相似度进行匹配并确定追踪的MCS回波轨迹。此处的相似度是指经过最大值归一化后的两个长度为14的样本特征之间的欧几里德距离。对于下一个时刻未匹配的MCS切片，则将其视为新追踪轨迹的起始，并为其分配新的MCS序号用于后续的追踪匹配。

如图4所示，分别计算MCS切片N与S1、S2的欧几里德距离，当前时刻切片N与下一时刻切片S1更相似，所以追踪轨迹指向S1（图中虚线箭头所指方向）。切片S2则被标记为新的MCS并用于后面的追踪，依此类推。显然，对于前后2个时刻只有一个重叠的切片，则该算法就类似于简单的重叠匹配；如果存在多个重叠切片，则选择最为相似的切片与现有的追踪轨迹相关联。

图4 追踪过程示意 （N为当前时刻的MCS切片，S1和S2为下一时刻的2个MCS切片）Fig.4 Tracking process （N is a MCS slice at the current moment，S1 andS2 are the two MCS slices at the next moment）

3.5 准线性MCS分类

根据准线性MCS的定义，首先用主观判断法从各MCS切片的雷达回波图中选择满足定义的准线性MCS；再根据追踪得到的MCS轨迹矢量，计算MCS正方向与轨迹矢量的夹角以及层状云和强对流云在拟合椭圆长轴两侧的占比，从而建立准线性MCS的分类算法。

（1）MCS正方向定义

定义沿x轴的正方向为基准，根据MCS切片的最佳拟合椭圆长轴的斜率k来确定椭圆短轴的正方向。若k≥0，则以右下侧短轴为正方向；若k＜0，则以右上侧短轴为正方向，如图5所示。

图5 MCS正方向的定义（a.k≥0，b.k＜0；红色箭头为短轴的正方向）Fig.5 Definition of the positive direction of MCS（a.k≥0，b.k＜0；red arrow is the positive direction of the minor axis）

（2）MCS分类特征计算

根据前述TS、LS和PS三种类型MCS的气象学特征，在此定义3个特征来实现3类MCS的分类，分别为短轴正方向与轨迹矢量的夹角（θ）、长轴两侧层状云区域面积比值（Rs）和长轴两侧强对流区域面积比值（RI）。RS和RI是正方向一侧的面积与负方向一侧的面积之比。轨迹矢量是当前MCS到下一时刻MCS的运动方向，在数学上，夹角的取值范围[0，180°]，此处为了区分正负方向的角度，当θ＞90°时，将其转换为θ−180°。此时，夹角（θ）的取值范围[−90°，90°]，其中[0，90°]表示MCS沿短轴正方向运动，[−90°，0]表示MCS沿短轴负方向运动。根据定义的上述特征对TS、LS和PS型MCS进行分类，如表5所示（表格中的thre是分类阈值，根据RI的计算结果及分类正确率，本试验thre的取值为10）。

表5 TS、LS和PS型MCS的分类规则Table 5 MCS classification rules for TS, LS and PS

4 试验结果

4.1 检验方法

文中试验属于有监督机器学习中的分类问题，所以用基于“观测”与“预测”按类别分类后列出频率表进行统计，通常将该表称为混淆矩阵（Zheng，2015），如表6所示。表中TP表示实际样本为MCS、模型预测也为MCS；FP表示实际样本为non-MCS、但模型将其预测为MCS；FN表示实际样本为MCS、但模型将其预测为non-MCS；TN表示实际为non-MCS、模型预测也为non-MCS。也就是说，TP和TN都是分类正确的度量值，而FP和FN都是分类错误的度量值。

表6 预测和实际标签的混淆矩阵Table 6 Confusion matrix for predictions and actual labels

根据混淆矩阵的统计结果，计算命中率（probability of detection，POD）、虚 警 率（false alarm ratio，FAR）、临界成功指数（critical success index，CSI）和准确率（accutacy，ACC）对结果进行综合评估。各评分标准的计算公式如下

4.2 MCS识别结果分析

使用训练好的SVM、RF、XGBoost和DNN四个模型分别对测试集样本进行MCS识别，得到各个模型的混淆矩阵，如表7所示。可以发现在测试集上，XGBoost模型对应的TP值最大，SVM模型对应的TP值最小，且二者相差较大，说明XGBoost模型对MCS类的识别效果最好，达到91.22%，而SVM模型对MCS类的识别效果最差，仅为88.10%。对于这一点，在FN上也得以很好的体现，在测试集的2732个MCS类样本中，SVM模型将其中325个样本预测为non-MCS，而XGBoost模型对应的该值为240。对于non-MCS类样本的预测，DNN模型取得了最高的准确率，对测试集中non-MCS类的分类正确率达到了90.16%，SVM模型仅次之。

表7 SVM、RF、XGBoost和DNN模型在测试集上的混淆矩阵Table 7 Confusion matrix of the SVM，RF，XGBoost and DNN models on testing set

混淆矩阵仅仅展示了模型预测效果的频率，为了更全面地对比这4个模型的分类性能，根据混淆矩阵计算它们各自的CSI、POD、FAR和ACC，如表8所示。DNN模型的CSI值最高，达到0.8034，这充分说明了DNN模型整体上对MCS类识别的性能优于其他模型，再结合ACC，更体现出DNN模型的优良性能。POD值反映了模型对正样本MCS类的识别率，XGBoost模型的POD值最高，达到0.9112，与前面对混淆矩阵的分析是极度吻合。而FAR值的大小反映了模型将负样本non-MCS类别识别为MCS类所占的比重，DNN模型的FAR值最小，说明其对non-MCS有很高的识别率。

表8 SVM、RF、XGBoost和DNN模型在测试集上的评分Table 8 Scores of the SVM，RF，XGBoost and DNN models on testing set

综合来看，DNN模型对MCS的识别性能优于其他3种机器学习模型，但该模型也存在一定缺点：对MCS类的识别正确率次于XGBoost和RF模型。考虑到后面的MCS轨迹追踪，若模型将non-MCS类预测为MCS类的次数较多，则会导致轨迹追踪出现一些属于非MCS的部分，对追踪结果正确性的影响会比较大；若模型将个别时刻雷达拼图中的MCS识别为non-MCS，中断的追踪路径可以重新再匹配进行连接，对整体的轨迹追踪不会有太大影响。因此，后面将选择使用DNN模型识别的MCS切片信息进行追踪，进而生成MCS条带数据。

4.3 MCS追踪结果分析

本节主要选取2个具体的MCS个例来分析追踪结果，分别发生在2019年5月17日09时24分—15时和2019年7月13日13时42分—22时54分。追踪结果的分析以下面原则为切入点：（1）若未匹配的追踪结果不连续，则重点分析断点处的雷达拼图是否为MCS；（2）若未匹配的追踪结果是连续的，则重点分析其轨迹起始处的雷达拼图是否为MCS。据此，对MCS生命期内的追踪结果进行主观分析。

（1）2019年5月17日MCS个例

图6显示了2019年5月17日的MCS发展演变过程，组成该MCS每个时刻的MCS切片样本由DNN模型识别，并且将分类阈值设置为0.5。当模型对样本的预测值不小于0.5时，将该样本对应的候选MCS切片进行追踪合并。该MCS始于09时24分，此时对流云团基本处于北京北部，并一路向南移动，至13时06分结束，持续近4 h，主要影响北京、廊坊和天津等地。

图6 2019年5月17日09时18分—15时MCS追踪轨迹Fig.6 Tracking path of MCS during 09：18—15：00 UTC 17 May 2019

该时段的MCS轨迹是不连续的（最下面有两条断开的轨迹）。查看实际雷达拼图数据发现，13时06—56分的雷达拼图数据缺失，但13时56分—14时30分的雷达数据正常，原始数据如图7所示，分割后的MCS切片如图8所示，并且DNN模型将其识别为MCS，生成的追踪数据也对该时段的MCS进行了关联。

图7 2019年5月17日13时56分—14时30分原始雷达拼图数据（a—f，时间间隔：6 min）Fig.7 Original radar mosaic data at 13：56—14：30 UTC 17 May 2019（a—f，interval：6 min）

图8 2019年5月17日13时56分—14时30分的MCS切片（a—f，间隔： 6 min）Fig.8 Display of MCS slices during 13：56—14：30 UTC 17 May 2019（a—f，interval：6 min）

试验结果表明，如果深度学习模型预测候选MCS样本的值未达到0.5，则会造成MCS的不连续，同时，某时段雷达拼图数据的缺失也会导致MCS的轨迹追踪中断，在这两种情况下时、空匹配过程将无法创建连续的MCS条带。尽管使用较高概率阈值的目的是减少non-MCS事件的错误识别，但实际情况表明，此方法也可能会删除或截断合理的MCS区域。由于匹配过程仅检查当前时刻和下一个6 min时刻的MCS切片匹配，因此，如果模型对某一个雷达拼图中的MCS切片的预测值未超过分类阈值，则追踪结束。

解决该问题的一种方法是重新分析追踪数据库来连接以前未连接的轨迹，也就是尝试将包含至少2个切片的条带末端（持续时间为12 min）连接到具有至少2个切片的条带开始端。要找到合适的匹配项，规定必须满足以下条件：（1）匹配的候选MCS条带的开始时间距上一个MCS条带的结束时间不超过60 min；（2）匹配的候选MCS条带的第一个切片与前一个条带的最后一个切片必须重叠或者相距100 km之内。图9是一个经过匹配的追踪轨迹，此时MCS的起止时间分别为09时24分和14时30分，很明显该MCS条带较未匹配前在结尾处有延伸（图9红色虚线标注区域），整个轨迹是连续的（与图6对比）。

图9 2019年5月17日09时18分—15时MCS追踪路径 （已匹配）Fig.9 Tracking path of MCS during 09：18—15：00 UTC 17 May 2019 （rematched）

（2）2019年7月13日MCS个例

图10显示了2019年7月13日的一个MCS过程，雷达观测该MCS大约始于13时42分，并一路向东南方向移动，途径北京、天津及河北东部，并经渤海湾进入山东省境内，至22时54分逐渐减弱消退，持续超过9 h。

图10 2019年7月13日13时42分—22时54分MCS追踪路径Fig.10 Tracking path of MCS during 13：42—22：54 UTC 13 July 2019

对DNN模型识别的MCS切片进行重新分析匹配，追踪轨迹如图11所示。显然，该MCS的轨迹较未匹配前有所延长（红色虚线标注区域），延长区域主要分布在河北省北部，并靠近北京市北部。这是由于DNN模型将某时刻MCS分类为non-MCS导致的中断，匹配后对其重新建立了连接。

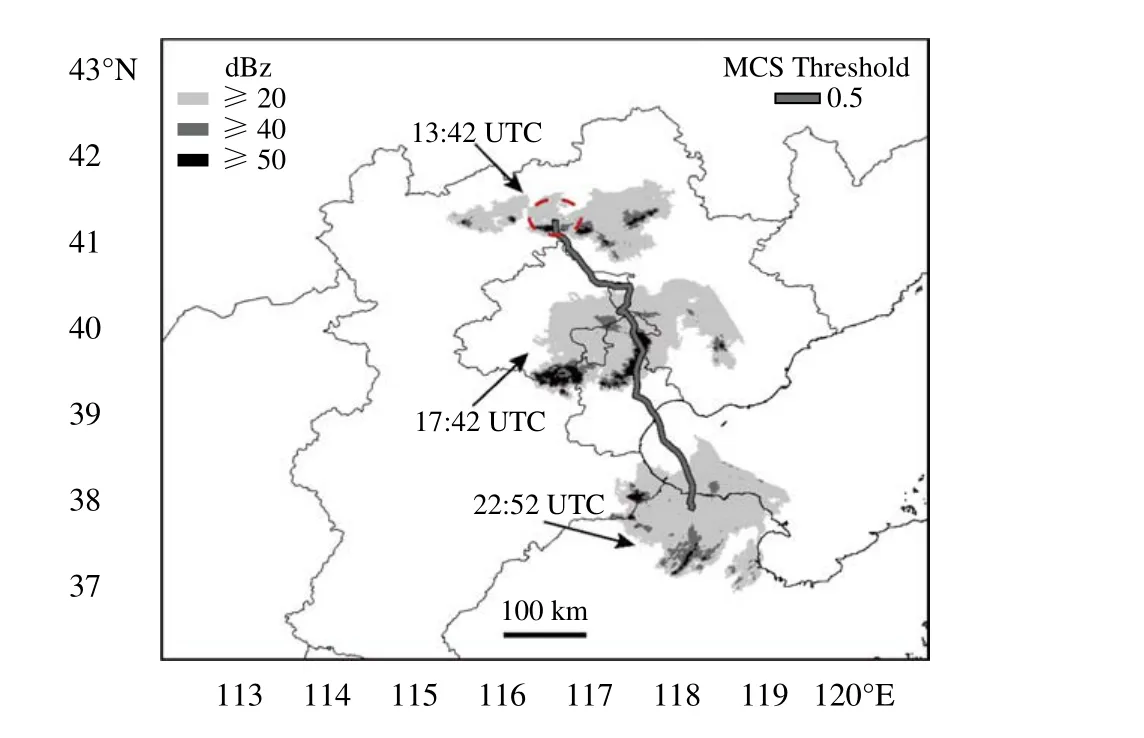
图11 2019年7月13日13时42分—22时54分MCS追踪路径 （已匹配）Fig.11 Tracking path of MCS during 13：42—22：54 UTC 13 July 2019 （rematched）

对上述MCS个例轨迹追踪中18时42分—19时11分的雷达数据（图12）和其所对应的MCS切片（图13）进行分析发现，雷达拼图分割时通常会得到一个候选MCS切片，但对于雷达回波结构和形态较为复杂的区域性对流天气过程，可能会出现2个（图13b—e，分割得到2个候选MCS切片）、有时甚至更多个候选切片。当子图中出现多个MCS切片时，表示在该区域的同一时段出现了多个MCS，进行追踪时会得到2条不同的轨迹路径。本试验的追踪结果只有1条，是因为发生在山东省北部的MCS切片虽然满足MCS的客观定义，但DNN模型将其识别为non-MCS，与雷达观测实际分析完全一致，图13b—e右下角的MCS切片回波特征只持续了24 min左右，无法形成真正的MCS。

图12 2019年7月13日18时41分—19时11分 （a—f，间隔：6 min） 的原始雷达拼图数据Fig.12 Original radar mosaic data during 18：41—19：11 UTC 13 July 2019 （a—f，interval：6 min）

图13 2019年7月13日18时41分—19时11分 （a—f，间隔：6 min） 的MCS切片展示（b—e子图中有2个MCS切片）Fig.13 Display of MCS slices during 18：41—19：11 UTC 13 July 2019 （a—f，interval：6 min）（there are two MCS slices in the b—e panels）

4.4 准线性MCS分类结果分析

根据3.5节的分类算法，对2018和2019年5—9月测试集数据的准线性MCS进行分类，可分为TS、LS和PS三类（表9）。统计结果显示，京津冀地区TS型在这3类准线性MCS中占据主体（71%左右）。Parker等（2000）的研究也表明，美国中纬度地区的准线性MCS以TS型为主。

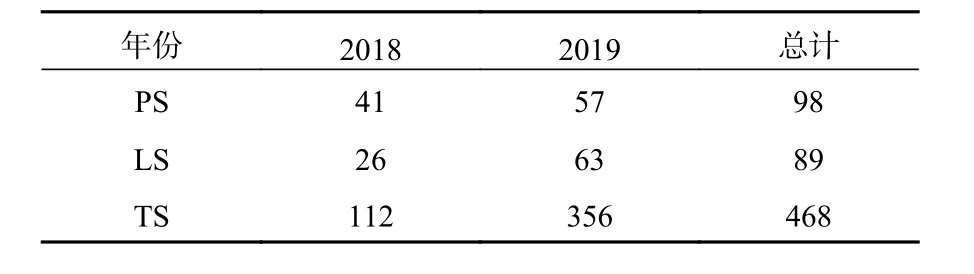
表9 2018和2019年MCS切片中TS、LS和PS型的个数统计Table 9 Numbers of TS，LS and PS in MCS slices in 2018 and 2019

为了分析试验结果，此处选择了3个时段的RS、RI和θ的计算值，分别与LS、TS和PS这3类准线性MCS对应，如表10所示。

（1）LS型：2019年5月17日12时41分—13时05分的MCS切片属于LS型。根据表5的分类算法，LS的类别由RI和θ决定。表10显示该MCS个例的RI值均小于0.1，且夹角θ值为正，与表5定义一致；结合MCS切片（图14，2019年5月17日12时41、47、53分和13时05分4个时刻的MCS切片），4个MCS切片整体向南移动，根据其对流和强对流区域的分布，判定为LS型。

图14 2019年5月17日的LS型MCS雷达回波（a.12时41分，b.12时47分，c.12时53分，d.13时05分）Fig.14 Classified LS MCS radar reflectivity on 17 May 2019（a.12：41 UTC，b.12：47 UTC，c.12：53 UTC，d.13：05 UTC）

续图14Fig.14 Continued

（2）TS型：2019年7月13日14时17分—15时59分的MCS切片属于TS型。表10显示该MCS个例的RI值均大于10，且夹角θ值为正，与表5对TS型的定义一致；结合MCS切片（图15，2019年7月13日14时17、47分、15时17和47分4个时刻MCS切片），4个MCS切片整体向南移动，根据其对流和强对流区域的分布，判定为TS型。

图15 2019年7月13日TS型MCS雷达回波 （a.14时17分，b.14时47分，c.15时17分，d.15时47分）Fig.15 Classified TS MCS radar reflectivity on 13 July 2019 （a.14：17 UTC，b.14：47 UTC，c.15：17 UTC，d.15：47 UTC）

（3）PS型：2019年7月25日05时47分—07时05分的MCS切片属于PS型。根据表5的分类算法，LS型由RS和RI决定。表10中该MCS个例的RS值均接近1，且RI值在[0.1，10]；结合MCS切片（图16，2019年7月25日05时47分、06时11、41分和07时05分4个时刻的MCS切片），发现与对流线相关的大部分层状云降水区域平行于该对流线，符合PS型特征。

图16 2019年7月25日PS型MCS雷达回波 （a.05时47分，b.06时11分，c.06时41分，d .07时05分）Fig.16 Classified PS MCS radar reflectivity on 25 July 2019 （a.05：47 UTC，b.06：11 UTC，c.06：41 UTC，d.07：05 UTC）

表10 分类出的LS、TS和PS型准线性MCS所对应的RS、RI和θ的计算值（比值的分母为0时用−9999.000表示计算值；此处只选择了3个时间段）Table 10 Calculated values ofRS，RI andθ，which correspond to the classified LS，TS and PS of Quasi-linear MCSs（−9999.000 is used to represent their values when the denominator ofRS andRI is 0，only three time periods are selected here）

综合以上分析发现，表5提出的TS、LS和PS分类算法取得了良好结果，证明该分类算法的合理性与可行性，为准线性MCS的自动客观分类提供了一种新的方法，可在强对流天气特别是强降水时、空特征的预报中得到应用。

5 结论与讨论

选取2010—2019年共10 a夏季的京津冀地区雷达拼图数据，基于机器学习开展了MCS的自动识别、追踪及分类试验研究。（1）对原始雷达拼图数据进行预处理以保证试验数据的有效性，根据PJ00标准按照特定的分割参数对原始雷达数据进行分割得到候选MCS切片，并从每个切片中抽取14个MCS特征值构建MCS特征识别数据集。（2）使用深度学习方法建立了一个二分类DNN模型，将预测结果与其他3种传统机器学习算法（RF、SVM和XGBoost）的结果进行对比。试验结果表明，DNN模型识别MCS的性能优于其他3种算法，能够有效判别MCS和non-MCS。并且，DNN模型将non-MCS识别为MCS的频率是最低的，有利于后续的MCS追踪。（3）将DNN模型识别的MCS切片用于MCS追踪，使用改进的时空重叠追踪法完成2018和2019年京津冀地区的MCS追踪，得到包含强度、空间和时间信息的MCS条带数据集。（4）根据追踪得到的MCS轨迹矢量计算MCS切片的运动方向，并求得MCS切片拟合椭圆长轴两侧的层状云和强对流云区域的面积占比，实现了TS、LS和PS三类准线性MCS的自动分类，对提升MCS致灾天气的预报、预警具有重要意义。

MCS回波结构复杂，对其进行有效识别在气象领域是一件较为复杂的工作。文中使用深度学习算法建立了自动识别MCS的方法，对MCS的研究具有重要意义。本研究还存在一些不足，如用搜索半径96 km来限定MCS切片的层状云区域，在以后工作中还需要继续改进；对MCS分块进行人工特征抽取，没有发挥卷积神经网络（Convolutional Neural Networks，CNN）自动抽取图像特征的优势；并且，对准线性MCS的分类也是基于人工抽取特征再进行映射而实现。因此，在未来的研究中，可以从以下两方面做深入探索：（1）CNN可以自动从输入数据中抽取到复杂的内在纹理特征，能够更加精确地捕捉到MCS分块中各个强度区域之间的空间联系，进行更高效地识别MCS。可以考虑使用CNN模型实现MCS切片的自动识别，但首先得解决CNN网络如何训练大小不同的MCS切片数据，或者解决如何将MCS切片数据的大小进行统一处理。（2）利用深度学习实现准线性MCS或者准线性对流系统（QLCS）中的TS、LS和PS型的特征分类（Parker，et al，2000）或实现MCS中强降水特征的分类识别（Schumacher，et al，2005，2020）。

致 谢：文中使用的机器学习算法源自Scikit-Learn开源库（代码地址：https://github.com/scikit-learn/scikit-learn.git）以及Google公司的TensorFlow平台（https://github.com/tensorflow/tensorflow.git），谨此致谢。