风电场风机覆冰期预报方法
2022-01-04许杨陈正洪
许杨 陈正洪
(1 湖北省气象服务中心,武汉 430205; 2 湖北省气象能源技术开发中心,武汉 430205)
引言
目前,风机覆冰作为影响风电场运营的重要灾害之一,国内外已开展的相关研究包括结冰气象条件模拟、积冰模型建立、结冰对风电功率预测的影响以及风机防冰除冰措施等[2-4]。本文主要开展风机覆冰期预报方法的研究,相关研究有Dierer等利用WFR镶嵌Mokkonen积冰模型开展了风机积冰预报[5];Davis等提出了利用WFR镶嵌Brakel模型预报冰重、覆冰类型,并可以与除冰模型融合的方法[6]。综合考虑多种预报方法发现,物理法没有考虑风机旋转对气场的影响;数值仿真模型虽然通过对气流轨迹进行模拟的基础上引入积冰模型,可以模拟风机桨叶各点覆冰量,但计算复杂,难以将连续变化的气象条件引入进行模拟。为此,本文拟采用Makkonen结冰增长模型镶嵌冰表面辐射融化模型建立适用于风机覆冰的预报模型,基于数值模拟结果和风机性能参数驱动模型,预报时考虑风机旋转时气流的相对速度,探索适用于实际业务运行的风机覆冰起止时间预报方法,为风电场前期效益风险评估及安全运行提供技术支撑。
1 资料与方法
1.1 资料
数值模拟资料为中国气象局公共气象服务中心提供的九宫山风电场代表点中尺度WRF耦合小尺度CALMET综合模式模拟结果,模式格点分辨率为1 km,时间分辨率为15 min,取预报当日北京时00:15之后72 h的模拟数据驱动模型,预报要素包括风速、风向、气温、相对湿度、气压。
风电场相关资料由通山九宫山风电场提供,包括16台风机覆冰起始时间数据、发电量数据、风机参数文件等。九宫山风电场风机型号为G58 850 kW的西班牙歌美飒双馈风力发电机。
1.2 预报模型建立
1.2.1 积冰模型
积冰模型分为经验模型[7]和物理模型[8]。物理模型一般有2种模拟方案:基于自由转动的垂直圆柱体的积冰模型和二维及三维叶片积冰仿真模型[2]。本研究由于侧重积冰起止时间模拟,不涉及冰形状模拟,因此采用Makkonen结冰增长数值模式[9-10]:
(1)
式中,M为结冰质量;t为结冰时间;v为粒子相对速度;w为粒子群含水量,即液态水含量LWC,可由WRF输出变量求算得到;A为有效积冰截面,与风向和有效粒子速度有关;α1为收集系数[11];α2为碰撞系数,当v<1 m/s,α2=1,否则α2=1/v;α3为增长系数[12]。
1.2.2 相对风速计算
综上所述,梅毒酶联免疫吸附法适合标本量比较大的检测,梅毒甲胺红不加热血清反应适用于梅毒治疗效果观察,梅毒螺旋体明胶颗粒凝集适用于梅毒甲胺红不加热血清反应和梅毒酶联免疫吸附法检出标本的验证检测,三种检测方式结合应用,可以降低误诊率与漏诊率,具有临床推广价值。
对旋转风机,Makkonen积冰模型中粒子相对速度Vrel,计算方法如下[13-14]:
(2)
(3)

1.2.3 融冰模型
融冰模型主要考虑对流辐射融冰[7],覆冰融化速率为:
(3)

1.3 模拟方案
考虑到覆冰持续时间可能超过气象要素预报时效,因此为确保实际业务应用的可行性,将覆冰开始、结束时间分别进行模拟预报,覆冰开始时间预报采用覆冰前3 d、前2 d、前1 d的数值天气预报结果驱动覆冰模型模拟[18];覆冰结束时间的预报需要先从覆冰开始时间模拟覆冰量,然后开展融冰模拟,因此预报时可以分别采取覆冰结束前3 d、前2 d、前1 d的数值天气预报结果驱动融冰模型,进行覆冰结束时间的预报。此外,在预报覆冰开始之后,假设风机停机,此后一直到覆冰结束期间,相对风速即为实际风速。
2 预报模型检验
2.1 模型的敏感性分析
利用G58 850 KW风力发电机相关性能参数,分别选择气温、风速、含水量、气压、相对湿度其中1个因子在一定范围内变化,其他因子保持固定值不变模拟风机积冰分别随气温、风速、液态水含量变化情况,以此对所建模型进行敏感性检验。
图1为结冰直径D=0.4 m,设计风速V=20 m/s,液态水含量w=0.3 g/m3时气温分别在-1 ℃、-3 ℃、-5 ℃、-7 ℃、-10 ℃、-20 ℃风机覆冰量随时间变化图。由图可见,覆冰初始阶段气温越低覆冰增长越快,最大覆冰量越少,达到最大覆冰量时间越短,越接近0 ℃最大覆冰量越大,达到最大覆冰量时间越长。模拟结果与理论结果一致,即气温越低,液态水冻结速率越快,主要以干增长为主,冰密度比较小,故最大积冰量小;气温接近0 ℃时以湿增长为主,初期液态水冻结少,但冰密度大且后期附着力强,因此最大覆冰量大。
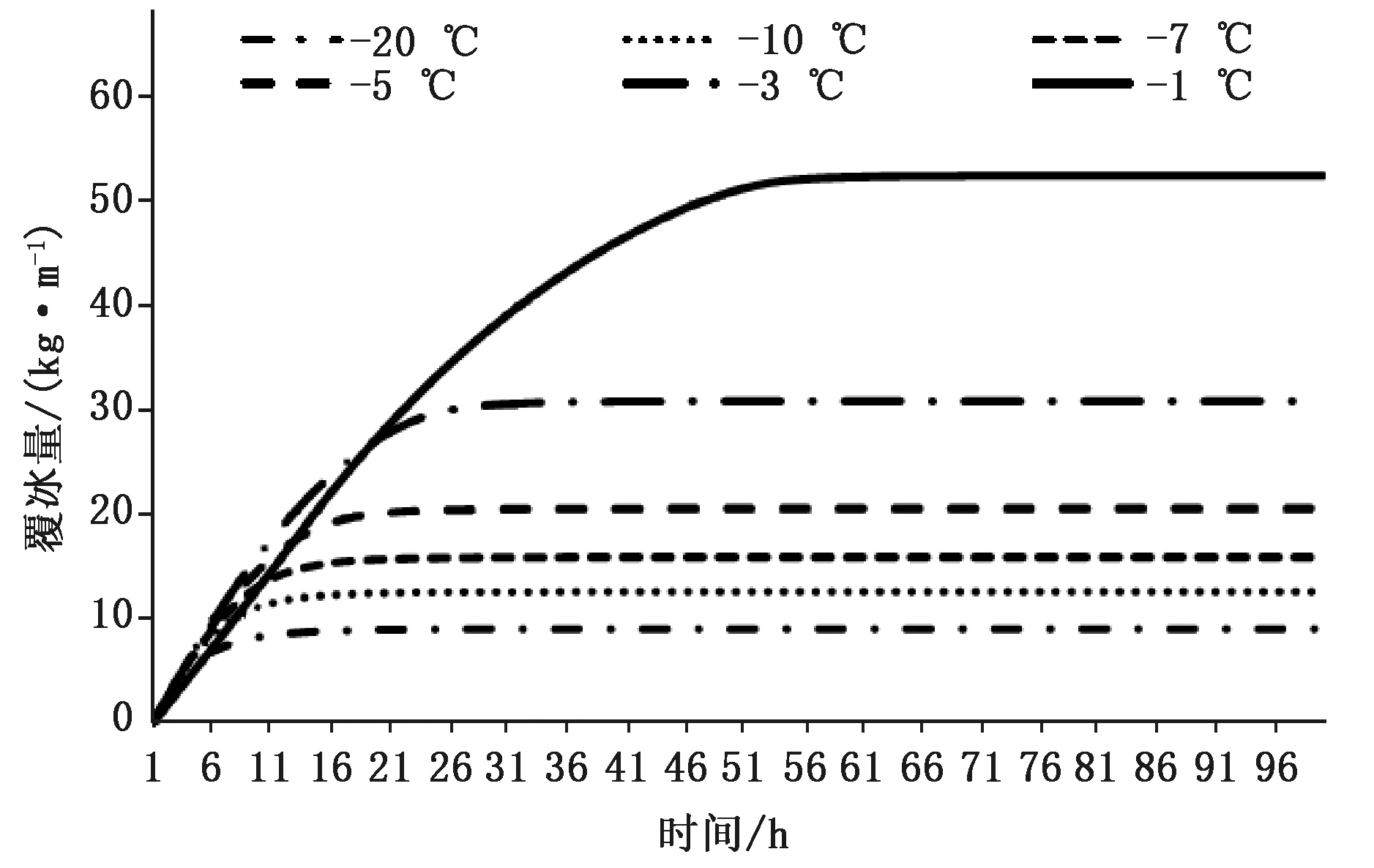
图1 设定D=0.4 m,V=20 m/s,w=0.3 g/m3,不同气温时覆冰量变化(D为结冰直径,V为设计风速,w为液态水含量,下同)
图2为D=0.4 m,气温T=-1 ℃,w=0.3 g/m3时风速分别在2 m/s、5 m/s、10 m/s、20 m/s、60 m/s风机覆冰量随时间变化图。由图可见,并非风速越大,覆冰增长越快,而是风速在适宜范围内覆冰增长速率随风速增加而增加,风速达到一定数值如60 m/s时,覆冰增长速率反而较慢,主要原因是风速越大水汽输送速率越高,但同时碰撞率越小,覆冰速率反而变小,当风速在适宜范围内时水汽碰撞率和冻结系数均较高,因此覆冰速率大。
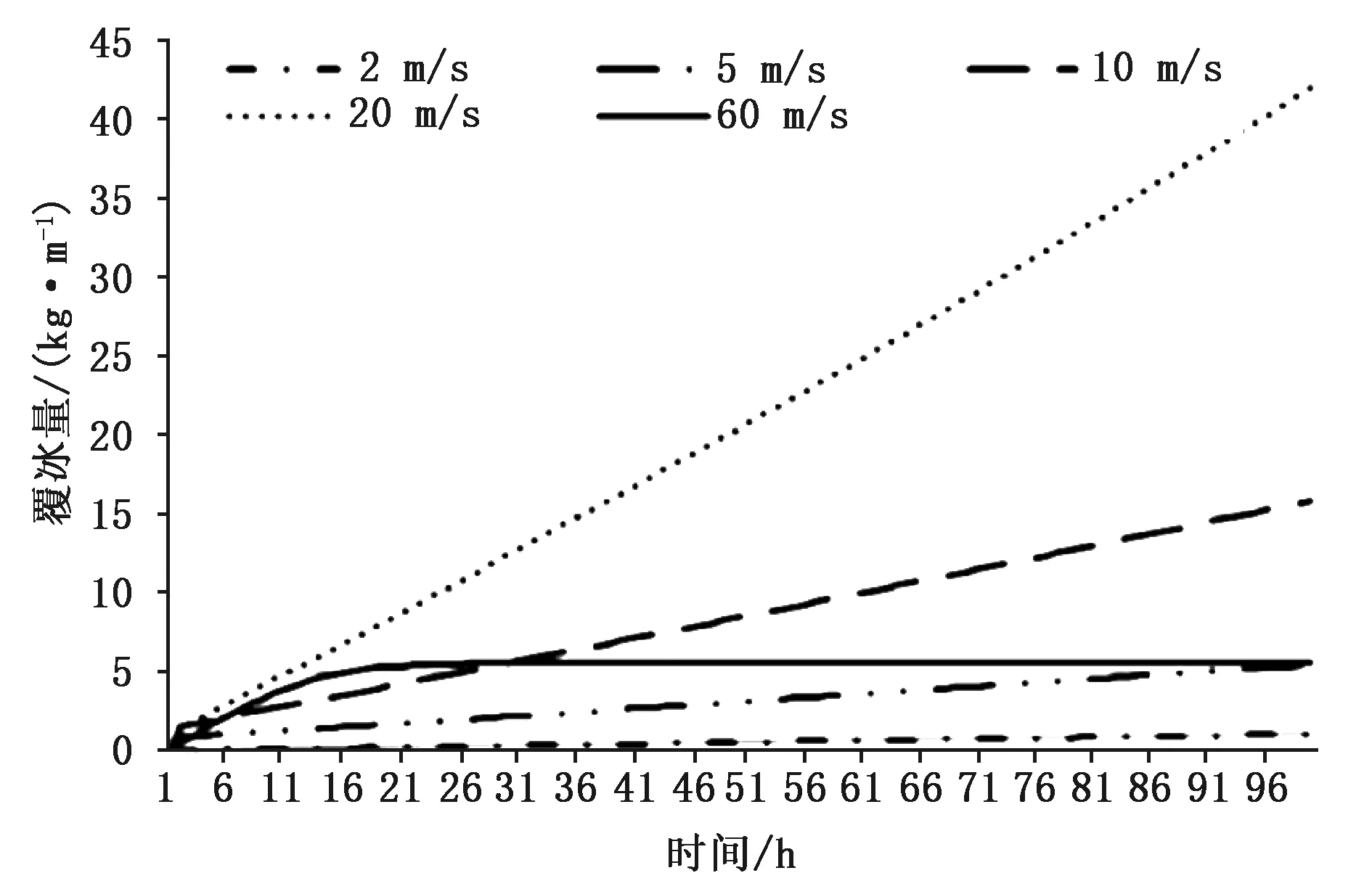
图2 设定D=0.4 m,T=-1 ℃,w=0.3 g/m3,不同风速时覆冰量变化(T为气温,下同)
图3为D=0.4 m,T=-1 ℃,V=20 m/s时液态水含量分别在0.1 g/m3、0.2 g/m3、0.3 g/m3时风机覆冰量随时间变化图。由图可见,液态水含量越高即水汽越充足,覆冰速率越快。

图3 设定D=0.4 m,T=-1 ℃,V=20 m/s,不同液态水含量时覆冰量变化
2.2 历史覆冰预报检验
以九宫山风电场2012年12月至2013年12月观测到风机(F1)共19次覆冰过程为研究对象,分别采用提前1 d、提前2 d、提前3 d三种预报方案,开展覆冰开始时间与结束时间预报,发现提前1 d、提前2 d、提前3 d三种预报方案能够同时报出覆冰发生及结束过程的次数分别为12次、8次、7次,提前1 d的报出率为63%。以下就覆冰开始和结束的预报结果分别进行分析及讨论。
表1为覆冰预报与实际开始时间对比结果,可见19次覆冰过程中提前1 d、提前2 d、提前3 d三种预报方案分别能报出13次、12次、12次,报出率在63%~68%;在预报出的覆冰过程中,提前1 d、提前2 d、提前3 d三种预报方案预报覆冰开始时间与实际覆冰开始时间平均相差6.8 h、27 h、38 h,发现越临近覆冰发生时间,覆冰开始时间预报准确率越高。提前1 d、提前2 d、提前3 d三种预报方案预报覆冰开始时间与实际覆冰开始时间相差6 h以内次数分别为7次、2次、2次;相差12 h以内分别为9次、3次、3次;相差24 h以内分别为13次、5次、5次。

表1 九宫山风场2012年12月至2013年12月覆冰过程开始时间预报检验
表2为覆冰预报与实际结束时间对比结果,可见提前1 d、提前2 d、提前3 d三种预报方案分别能报出15次、9次、9次,报出率分别为79%、47%、47%;在预报出的覆冰过程中,提前1 d、提前2 d、提前3 d三种预报方案预报覆冰结束时间与实际覆冰结束时间平均相差18 h、15 h、18 h;提前1 d、提前2 d、提前3 d三种预报方案预报覆冰结束时间与实际覆冰结束时间相差6 h以内次数分别为3次、2次、1次;相差12 h以内分别为5次、4次、2次;相差24 h以内分别为10次、7次、6次。

表2 九宫山风场2012年12月至2013年12月覆冰过程融化时间预报检验
覆冰结束时间预报误差大于覆冰开始时间,主要是因为覆冰结束时间预报需要从覆冰开始时间模拟覆冰量,再运行融冰模型,开展覆冰结束时间预报,覆冰量预报误差以及融冰模型的误差均会影响覆冰结束时间误差,且目前融冰模型仅考虑了表面辐射融冰的情况,而辐射融冰仅仅是融冰的一种原因,除此之外还包括机械融冰、传导融冰等导致融冰发生。提前1 d、2 d、3 d无明显改善,说明覆冰量和融冰模型比气象数值预报精度对覆冰结束时间更敏感,影响更大。
2.3 典型覆冰过程预报
典型过程1:2012年12月17日16:48至2012年12月19日14:31 F1风机出现近2 d的覆冰,模型对覆冰开始时间和结束时间预报结果如图4所示。此次过程提前2 d、提前3 d均未报出覆冰开始时间,但提前1 d预报方案可以预报出覆冰开始时间,比实际覆冰时间滞后6 h;提前1 d、2 d、3 d预报方案均报出了融冰时间,与实际观测融冰时间基本无差异,分别相差1 h、0 h和3 h。分析覆冰期气象条件(图5)可以知道覆冰发生时气温低于0 ℃,相对湿度达到100%,液态水含量维持在1.0 g/m3,风速在7.5 m/s左右;0 ℃以上覆冰开始融化,2 h左右完全融化。
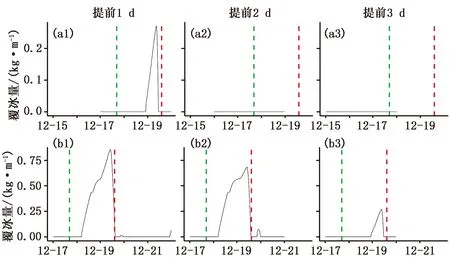
图4 提前1 d、2 d、3 d预报的2012年12月17日覆冰开始(a1~a3)和结束(b1~b3)时间及覆冰量(绿色虚线为覆冰开始时间,红色虚线为覆冰结束时间,下同)

图5 2012年12月17日预报覆冰及气象要素:(a)覆冰量,(b)相对风速,(c)风速,(d)气温,(e)液态水含量,(f)相对湿度
典型过程2:2013年1月2日20:00至2013年1月9日18:00出现了长达1周左右的覆冰,模型对覆冰开始时间和结束时间预报结果如图6所示。此次过程提前2 d、提前3 d均未报出覆冰开始时间,但提前1 d预报方案可以预报出覆冰开始时间,比实际覆冰时间提前18 h;提前2 d、3 d预报方案均未报出融冰时间,提前1 d预报方案报出了融冰时间,比实际观测融冰时间推迟17 h。分析覆冰期气象条件(图7)可知覆冰发生时气温低于0 ℃,相对湿度仅60%,液态水含量几乎接近0.1 g/m3,风速10 m/s左右,覆冰发生较快;覆冰期间多次气温回升到0 ℃以上,覆冰部分融化,但之后覆冰重新增长,直到气温持续一段时间高于0 ℃,覆冰才完全融化。

图6 提前1 d,2 d,3 d预报的2013年1月2日覆冰开始(a1~a3)和结束(b1~b3)时间及覆冰量
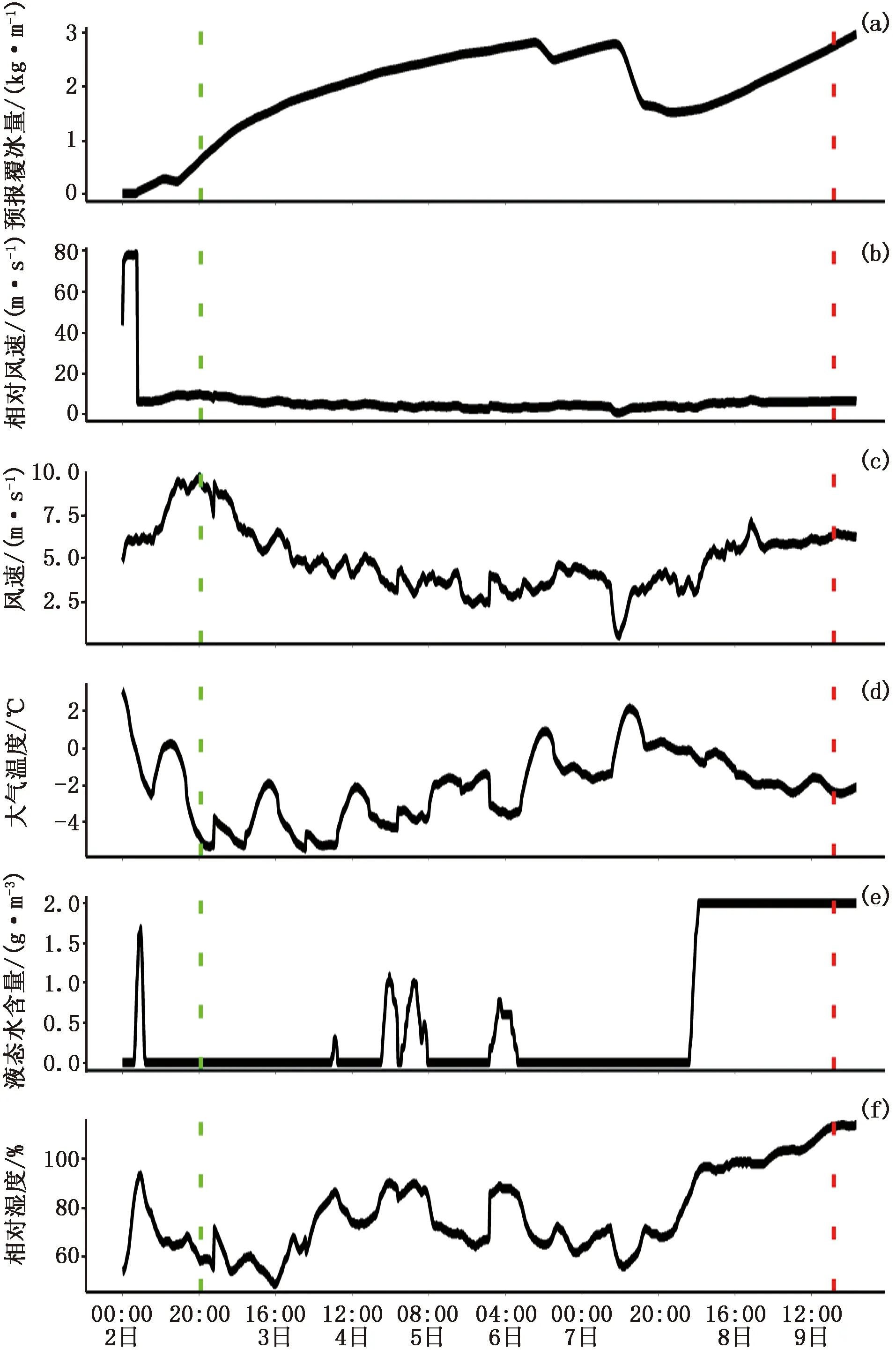
图7 2013年1月2日预报覆冰及气象要素:(a)覆冰量,(b)相对风速,(c)风速,(d)气温,(e)液态水含量,(f)相对湿度
分析以上两次典型覆冰过程可见,按照气温0 ℃以下,相对湿度85%的阈值作为风机覆冰开始判断指标并不完全适用,气温0 ℃以下是覆冰开始的必要条件,但不是唯一条件,综合考虑敏感气象要素及风机气动参数的覆冰模型在覆冰预报中表现出更好的预报技巧性和可操作性。0 ℃以上作为融冰条件仅能判断覆冰开始融化,但并不能预报覆冰融化时间,镶嵌融冰模型的覆冰预报模型考虑覆冰量和融冰速率,在覆冰结束时间预报上较阈值法优势更明显。
3 结论与讨论
本文采用Makkonen结冰增长模型镶嵌冰表面辐射融化模型建立适用于风机覆冰的预报模型,基于WRF耦合Calmet综合模式预测结果和风机性能参数驱动模型,进行风机覆冰开始和结束时间的预报。以湖北通山九宫山风电场为研究对象,采用该区域气象自动站观测数据对数值模式结果系统性误差进行修正,在此基础上对预报模型的准确性进行检验评价。
(1)风电场2012年12月至2013年12月两年中观测到风机(F1)共发生覆冰19次,分别采用提前1 d、提前2 d、提前3 d三种预报方案,开展覆冰起止时间的预报,并与实际覆冰起止时间进行比较,发现提前1 d、提前2 d、提前3 d预报开始时间分别能报出13次、12次、12次,预报结束时间分别能报出15次、9次、9次,提前1 d的报出率约为79%。
(2)在预报出的覆冰过程中,提前1 d、提前2 d、提前3 d三种预报方案预报覆冰开始时间与实际覆冰开始时间平均相差6.8 h、27 h、38 h,预报覆冰结束时间与实际覆冰结束时间平均相差18 h、15 h、18 h,说明越临近覆冰发生时间,覆冰开始时间预报准确性越高。
(3)提前1 d、提前2 d、提前3 d三种预报方案预报覆冰开始时间与实际覆冰开始时间相差6 h以内次数分别为7次、2次、2次,相差12 h以内分别为9次、3次、3次,相差24 h以内分别为13次、5次、5次。
以上分析说明本模型对风机覆冰具有一定的提前预警能力,覆冰结束时间预报误差大于覆冰开始时间,主要是因为覆冰结束时间预报需要从覆冰开始时间模拟覆冰量,再运行融冰模型,然后开展覆冰结束时间预报,覆冰量预报误差以及融冰模型的误差均会影响覆冰结束时间预报效果,且目前融冰模型仅考虑了表面辐射融冰的情况,而辐射融冰仅仅是融冰的一种原因,因此对融冰模型进行改进或将实际覆冰量作为模型输入可以提高覆冰结束时间的预报精度。模型中参数较多,需在实践中不断改进,对参数算法进行优化,采用更精细准确的数值预报结果驱动,以期获得更好的预报效果。
