基于多目标FCS-MPC的永磁同步发电机MTPA控制

邱建琪，吴翊铭，史涔溦

(浙江大学 电气工程学院，浙江 杭州 310027)

永磁同步发电机PMSG由于结构简单、效率高及可靠性高等优点，在现代工业中被广泛使用。由于PMSG输出交流电压，其幅值和频率随着转速变化而变化，因此在PMSG的输出端需要通过整流器将交流电压变换成稳定的直流电压，从而保持输出电压的稳定。常用的整流方式有二极管不控整流和脉冲宽度调制(pulse width modulation，PWM)整流2类。

目前对于永磁同步发电机PWM整流的常用控制策略是电压外环和电流内环的双闭环PI矢量控制，根据d，q轴电流分配策略，又可以分为id=0控制、最大转矩电流比MTPA控制和弱磁控制等。但在实际PI控制中，控制效果对系统参数的依赖度很高，且不同工况下最优PI参数不同，因此在变工况控制情况下控制效果欠佳[1-4]。

近年来，有限集模型预测控制FCS-MPC由于其结构简单、多目标控制及良好的非线性控制效果等特点被广泛应用在永磁同步电机控制领域中。FCS-MPC根据系统模型，预测有限集合中每个控制组合作用下在未来周期中被控变量的变化，通过代价函数计算得到最优控制组合，实现被控变量对参考变量的跟踪。该算法响应迅速、鲁棒性强，能够有效克服PI控制中参数整定复杂、受环境影响等缺点。目前,已有大量文献开展了针对永磁同步电动机PMSM的FCS-MPC控制的研究，然而在发电系统中，目前对于PMSG稳压控制的预测控制研究较少，故PMSM的预测控制策略对基于PWM整流器的PMSG稳压控制具有较大研究意义[5-7]。

对于永磁同步发电机的id=0控制，可以采用基于电流模型预测的方法实现，即通过给定d，q轴电流计算电流代价函数从而得到最优电压矢量[8]。在中低速工况下，对于永磁同步凸极发电机系统，通过MTPA控制策略，可以最大限度提高效率，在保证有效输出同时降低相电流，有利于开关器件工作。为了实现MTPA，需要先计算得到某个转矩参考下的d，q轴电流参考值，然后基于矢量控制或者电流模型预测控制来实现后续的电压矢量分配[9]。课题组针对上述方法，提出了一种基于多目标FCS-MPC的永磁同步发电机MTPA控制方法，在FCS-MPC基础上，通过多目标优化实现转矩参考值跟踪及MTPA优化控制，可以代替传统的基于双闭环PI的矢量控制及电流模型预测控制，具有较强的鲁棒性和良好的动静态性能。

1 PMSG稳压系统

永磁同步发电机稳压系统的拓扑如图1所示，包括PMSG、PWM整流器、电容及直流负载。原动机拖动电机转动，输出三相交流电压，通过PWM整流器和电容转换成稳定的直流电压，供给负载。

图1 PMSG系统拓扑Figure 1 Topology of PMSG system

在电动机惯例下，PMSG在同步旋转坐标系中的模型如下：

(1)

电磁转矩方程为：

Te=1.5pn[ψfiq+(Ld-Lq)idiq]。

(2)

式中：ud，uq为定子d，q轴电压；id，iq分别为定子励磁电流、转矩电流；Rs为定子电阻；Ld，Lq为电机d，q轴电感；ω为电机的电角速度；ψf为永磁体磁链；pn为电机极对数;Te为电机的电磁转矩。

当控制周期足够小时，可以认为模型的各个变量在控制周期中保持不变，采用欧拉算法可对式(1)进行离散化，离散公式如下：

(3)

式中Ts为采样周期。

将式(3)代入式(1)，可得PMSG的离散数学模型为：

(4)

式中：k为当前采样周期，k+1为下一采样周期；ud(k)，uq(k)分别为当前周期定子电压d，q轴分量；id(k)，iq(k)分别为当前周期定子电流d，q轴分量；id(k+1)，iq(k+1)分别为下一周期定子电流d，q轴分量。

2 控制优化目标

2.1 转矩控制

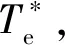
转矩预测的模型可由式(2)得出：

Te(k+1)=1.5pn[ψfiq(k+1)+(Ld-Lq)id(k+1)iq(k+1)]。

(5)

式中Te(k+1)为下一周期的转矩预测值。

(6)

在系统的每个周期中，保证电磁转矩的代价函数最小，能够有效地实现转矩跟踪。

2.2 MTPA控制的实现

为了提高PMSG稳压系统的控制效率，当原动机运行在中低速工况下，期望通过最小的定子电流产生最大的电磁转矩满足负载的需求，即对PWM整流器采用最大转矩电流比MTPA控制。

设定子电流矢量is与d轴呈θ角度关系，则电流在d,q坐标系下的电流分量分别为：

(7)

式中is为定子电流幅值。

将式(7)代入式(2)得：

(8)

以定子电流幅值不变为条件，为了实现电机的最大电磁转矩输出，需要得到最优的夹角θ，即求取式(8)以θ为变量的极值点，应满足：

(9)

联立式(7)和式(9)可得：

(10)

由式(10)可得到永磁同步发电机MTPA控制时的运行轨迹，如图2所示[10]。

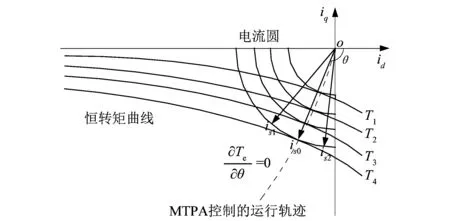
图2 永磁同步发电机MTPA控制的运行轨迹Figure 2 Track of PMSG MTPA control

如图2所示，永磁同步发电机的恒转矩曲线集中在第3象限，MTPA的运行点为电流极限圆与恒转矩曲线的切点，各切点构成了MTPA的运行轨迹。

课题组将MTPA控制与永磁同步发电机的FCS-MPC算法结合，通过增加一个目标优化项，实现PMSG的MTPA预测控制。建立MTPA的代价函数如下：

(11)

由式(10)和式(11)可知，为了实现MTPA控制，使工作点位于MTPA轨迹上，应控制代价函数fMTPA尽可能接近0。

2.3 最大电流约束

为了保证开关器件和永磁同步发电机系统的安全，需要约束允许通过的最大电流，令最大电流为imax,具体方式为在代价函数中引入一个限流辅助项如下：

(12)

当电机的定子电流幅值小于等于imax时，系统并无过流，此时限流代价函数为0；当定子电流幅值大于imax时，系统存在过流危险，此时代价函数产生作用，限流保护开启，通过多目标代价函数的作用，控制系统电流小于限幅值。

3 多目标优化实现

3.1 多目标优化代价函数

由上文可知，为了实现永磁同步发电机PMSG稳压系统的MTPA控制，控制方法中包含多个优化目标，为了实现多目标优化，设计系统的代价函数为：

f=KTefTe+KMTPAfMTPA+Kimaxfimax。

(13)

式中：KTe，KMTPA，Kimax为对应代价函数的权值系数，通过调试权值系数可以得到最优的多目标优化效果，并且在变工况后也无需调节系数。

在系统的动态过程中，转矩误差较大，此时电磁转矩代价函数起主导作用，实现转矩的快速跟踪。在系统的稳态过程中，转矩跟踪基本实现，MTPA优化代价函数起主导作用，系统将根据此刻的负载工况进行电流的调节，确保PMSG稳压系统始终保持在MTPA运行轨迹上。电流约束代价函数则一直约束定子电流在安全范围内，用于保护开关器件和电机的安全，避免因过流造成系统损坏[11]。

3.2 矢量集约束

在FCS-MPC控制算法中，对于三相PWM整流器，由于每相桥臂有2种开关状态，所以矢量集一共包括8种电压矢量，8种电压矢量对应的开关状态如图3所示。

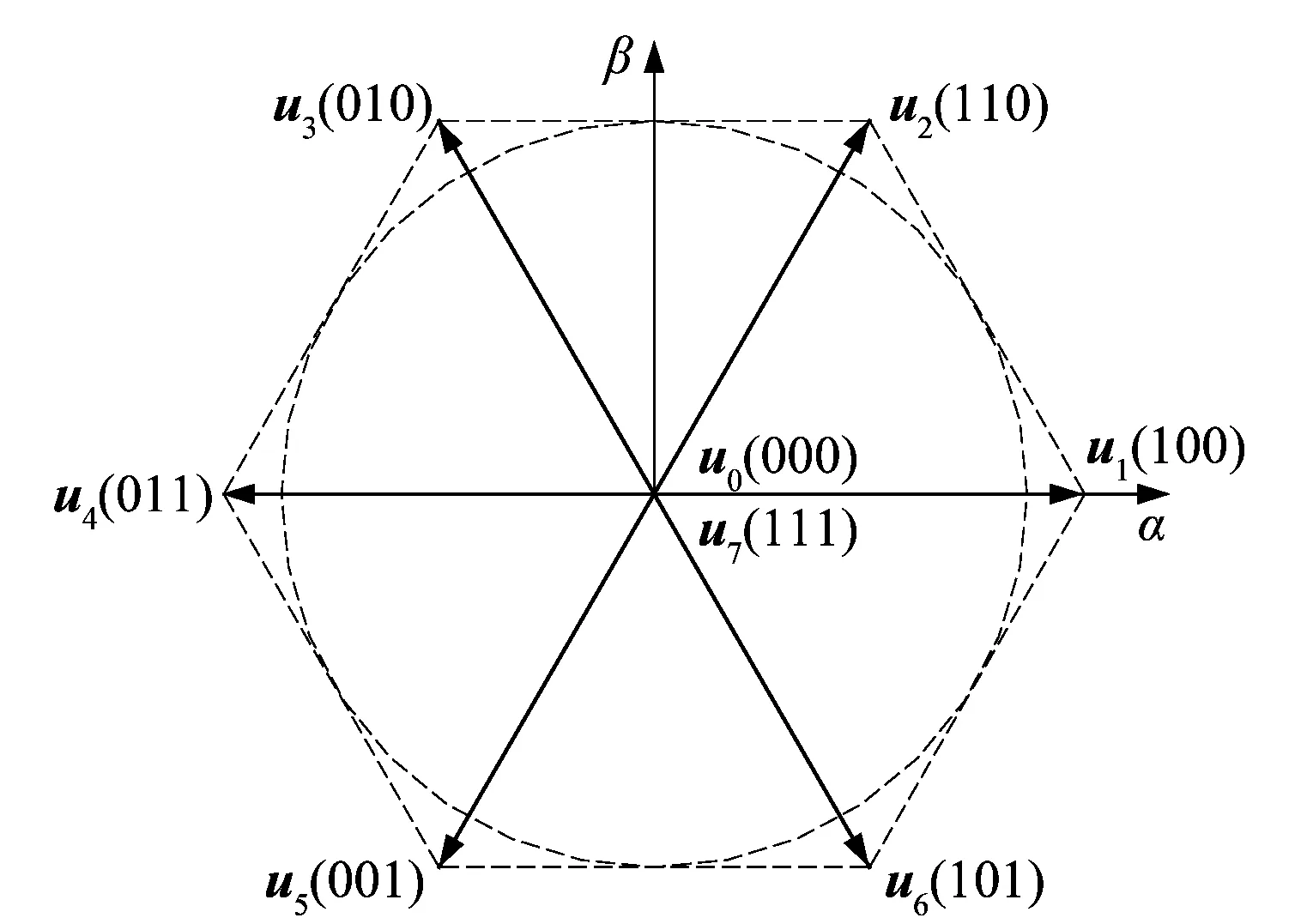
图3 三相PWM整流器的8种电压矢量Figure 3 Eight voltage vectors of three-phase PWM rectifier

传统的基于电流模型预测的id=0控制框图如图4所示，由当前电流值预测下一时刻的电流值，电压外环输出iq给定值，计算电流代价函数fid和fiq，通过计算不同电压矢量作用下的电流代价函数，得到最优电压矢量，并转换成开关信号作用于PWM整流器。

图4 基于电流模型预测控制的PMSG的id=0控制框图Figure 4 Control block diagram of PMSG id=0 control based on current model predictive control

图5所示为本文控制方法的框图，由当前时刻电流值预测下一时刻的电流值和转矩值，电压外环输出转矩参考值后，分别计算不同电压矢量作用下的多目标优化代价函数，并选取使代价函数最小的电压矢量，通过PWM整流器开关器件实现系统的控制。

图5 基于FCS-MPC的PMSG的MTPA控制框图Figure 5 Control block diagram of PMSG MTPA control based on FCS-MPC

4 仿真分析

为了验证课题组所提控制方法的正确性与可行性，在MATLAB/Simulink平台上对PMSG稳压系统进行了仿真。系统参数如表1所示。

表1 PMSG参数Table 1 Parameters of PMSG

课题组对永磁同步发电机稳压系统，分别进行基于电流模型预测的id=0控制仿真，及基于多目标FCS-MPC的MTPA控制仿真，并进行对比。

仿真系统的主要参数如下：给定母线电压参考值为100 V，相电流限幅为5 A，稳态工况时原动机转速为350 r/min，负载为100 Ω。为了验证系统的动态性能，进行了卸载和加速的仿真。稳态和动态的波形如图6所示。

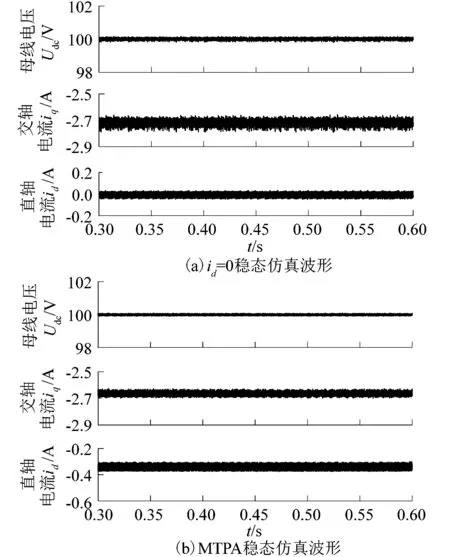
图6 PMSG基于电流模型预测的id=0控制和基于多目标FCS-MPC的MTPA控制的仿真波形Figure 6 Simulation waveforms of PMSG id=0 control based on current model prediction and MTPA control based on multi-objective FCS-MPC

图6所示的仿真中，卸载仿真即在稳态运行时，将100 Ω负载突卸至空载，加速仿真即在稳态运行时，将350 r/min的原动机转速突增至500 r/min。

由图6(a)和(b)可知：当系统处于稳态时,直流电压均稳定在给定值，采用文中提出的多目标FCS-MPC方法进行控制时，为了提高运行效率，MTPA优化目标项控制励磁电流id=-0.34 A,由id，iq可得定子电流幅值ia=2.69 A，小于id=0控制时的2.75 A，有效优化了系统效率，实现了永磁同步发电机整流系统的MTPA控制。

由图6(c)和(d)可知：在0.45 s时刻系统突卸负载后，通过文中提出方法进行控制，约0.04 s后系统稳定运行在新的工况，id稳定在0 A，且直流电压的跟踪效果较为良好。随着负载的改变，励磁电流id可以实现有效自适应调节。

由图6(e)和(f)可知：在0.45 s时刻原动机突增转速后，通过多目标FCS-MPC方法，经过0.03 s的动态变化，电压仍稳定在给定值，id变为-0.13 A，定子电流幅值仍小于id=0控制时的幅值，实现了系统的MTPA控制。由图可知，由于此时转速较高，MTPA控制的电流稳定性优于id=0控制。

仿真结果表明：采用多目标FCS-MPC方法进行MTPA控制，系统运行状况稳定，动态响应平滑，随着负载和转速的变化，励磁电流id可以实现自适应调节，使整个运行过程中系统始终能运行在MTPA轨迹上，有效实现了永磁同步发电机系统的MTPA控制。

5 实验验证

对上述仿真分析进行实验验证。实验所用硬件平台如图7所示。图7(b)中，测功机起原动机作用的。

图7 系统硬件平台Figure 7 System hardware platform

在Keil软件中分别编写id=0电流预测控制和多目标FCS-MPC的MTPA控制程序。由于实际实验中，计算与采样都不能实时完成，不能忽略，故实验中对系统延时进行了补偿，即通过计算下一个采样周期的代价函数来进行滚动优化。

实验中设置开关频率为16 kHz，PWM整流器输出外接100 Ω电阻，给定直流母线电压为100 V，稳态实验转速为350 r/min。在实验中，由于硬件平台非理想情况，无法做到绝对空载，且开关器件对开关频率有限制，与仿真相比存在误差电流。

稳态实验波形如图8(a)和(b)所示。稳态运行时系统突卸负载至空载，得实验波形如图8(c)和(d)所示。在稳态运行时，突增转速至500 r/min，记录实验波形如图8(e)和(f)所示。

图8 PMSG基于电流模型预测的id=0控制和基于多目标FCS-MPC的MTPA控制的实验波形Figure 8 Experiment waveforms of PMSG id=0 control based on current model prediction and MTPA control based on multi-objective FCS-MPC

由图8(a)和(b)可知，当系统处于稳态时,直流电压均能较好地稳定在给定值，采用多目标FCS-MPC方法进行控制时，id=-0.25 A,且通过id，iq计算定子电流幅值ia=3.3 A，小于id=0控制时的3.7 A，有效实现了永磁同步发电机整流系统的MTPA控制。

对比图8(c)和(d)得到：在卸载实验中，系统突卸负载后，通过课题组提出方法进行控制，id变为0 A且基本稳定在0 A，并能有效跟踪直流电压给定，动态响应平滑。

对比图8(e)和(f)可知：在加速实验中，原动机突增转速后，通过多目标FCS-MPC方法，电压仍稳定在给定值，id仍为负值，仍实现了系统的MTPA控制，由于原动机加速过程的影响，响应速度与仿真有差距，但动态响应平滑，证明MTPA优化有良好的动静态性能。

6 结语

课题组提出了一种基于多目标FCS-MPC实现永磁同步发电机MTPA控制的方法，通过设计基于MTPA曲线的代价函数，无需实时计算得到MTPA曲线上的id，iq数值，直接实现MTPA控制的FCS-MPC，并与基于电流模型预测的id=0控制进行比对，进行了仿真分析和实验验证。仿真和实验结果表明，通过多目标FCS-MPC，可以实现电磁转矩跟踪、MTPA优化控制及最大电流约束，从而有效跟踪给定直流母线电压。该方法既能优化系统的运行效率，又使系统具有良好的稳定性，并且动态响应迅速平滑，实现了永磁同步发电机的MTPA控制。