废石-尾砂胶结膏体料浆的压力泌水效应及管输边界层厚度估算
2022-01-04杨天雨乔登攀
杨天雨 乔登攀 邓 涛 王 俊 张 希
(1.昆明理工大学 国土资源工程学院,昆明 650093;2.玉溪矿业有限公司 大红山铜矿,云南 玉溪 653100)
目前,膏体充填以其浓度高、屈服应力高、充到井下不分层、泌水量少、重金属离子不随着泌水而迁移的特点得到广泛应用。众所周知,管道输送是将膏体料浆输送到井下的有效途径,充填膏体拌合物在管道压力作用下必然有一部分水分(包括稀浆)被挤出,从某种意义上来说,这正是充填膏体管道输送的必要条件。一定量的水分或稀浆的泌出,对形成柱塞流所必需的润滑层起着决定性的作用,该润滑层即为管道输送边界层。所谓柱塞流(又称栓流),就是指宾汉姆体沿管道作层流流动时,物体中心部分由于其屈服值大于剪应力而形成一固体塞(或称固体栓),塞内不存在速度梯度,整体是以同一速度作向前运动的流动状态[1]。在充填料浆管输边界层效应方面,滕一峰等[2]参考平板层流卡门动量积分关系并结合工程实践求得管道非连续流体的层流卡门动量积分和边界层厚度表达式;刘晓辉等[3]基于非牛顿流体力学及表观滑移假说,通过理论分析将膏体管内流动划分为柱塞区、剪切区及滑移区,结合宾汉流变模型,构建膏体管道输送的流量平衡方程,推导出膏体管内滑移流动的阻力公式。肖建华[4]引入理论力学给出的大变形非线性运动方程从而得到用截面宏观流速场确定边界层位置的方程;YANG等[5]研究了变厚度拉伸薄板上的分数阶边界层流动与传热问题;彭阳生等[6]利用多物理场的方法模拟粒子在二维圆管湍流中的运动分布规律;吕馥言[7]以煤泥为测试物料,对边界层性质以及基于边界层变化的管输特性对阻力损失的影响进行单因素研究和多因素分析,系统研究了管道特征及边界层性质改变对管道输送减阻率的影响;KALYON等[8]对浓度60 vol%的硫酸铵颗粒悬浮液进行壁面滑移的试验研究,认为主要与颗粒粒径有关,且值约为颗粒平均粒径的0.06倍;JANA等[9]对浓度为46 vol%~52 vol%内的聚乙烯颗粒悬浮液进行试验,发现边界层厚度值约为平均粒径的0.063倍;YARAS等[10]在研究中发现了类似现象,即边界层厚度值的大小实质上取决于浆体中固体颗粒的填充程度以及颗粒的平均粒径,并且提出边界层厚度与平均粒径的比值之间存在一定的数学关系;宁宇等[11]对比了移动壁面的边界层发展规律与固定壁面的情况,认为两个边界层内Vy的方向相反,对边界层发展的作用方向相反。常青林[12]利用黏性流体相关理论并结合施利希廷平行管道边界层研究成果,推导出了水平放置的平板间边界层流体速度计算公式;王小云等[13]基于滑移长度模型,理论推导出滑移长度随流体黏度及薄膜厚度的变化关系;徐世杰等[14]由边界层相似理论,考虑壁面倾斜角度和黏性的影响,设计了边界层水流速度可视化方案,建立了可视化模型,通过投影法显示了层流边界层流动状态;刘晓辉[15]根据表观滑移的定义,推导出滑移层厚度估算公式。
综上所述,膏体料浆在管道输送过程中在管壁处存在边界层效应,且边界层的成因为膏体料浆在管道内的压力泌水效应,现有成果没有将边界层效应与压力泌水效应结合起来考虑,本文从充填膏体管输边界层的成因着手,通过对废石尾砂胶结膏体料浆进行压力泌水试验及侧限压缩试验,进而建立膏体压力泌水率的计算模型,并提出边界层厚度的估算方法,本文的研究成果可对高浓度粗细颗粒混合胶结充填料浆的管输阻力研究提供借鉴意义。
1 充填膏体的侧限压缩试验与压力泌水试验
1.1 试验材料
本次试验材料选用某矿山废石尾砂,尾砂松散堆积密度1.328 t/m3,表观密度2.841 t/m3,堆积密实度为0.468,空隙率为0.532,加权平均粒径dp为57.78 μm,尾砂化学成分见表1。本次试验所用废石采用该矿山露天采场矿体下盘剥离废石,废石以白云岩为主,平均密度为2.754 t/m3,松散堆积密度1.75 t/m3,堆积密实度为0.635 5,空隙率0.364 5;水泥采用普通硅酸盐425#水泥。

表1 尾砂化学成分表Table 1 Chemical compositions of tailings
将废石尾砂按照一定比例混合,两种骨料混合后的堆积密实度及混合料密度见表2。
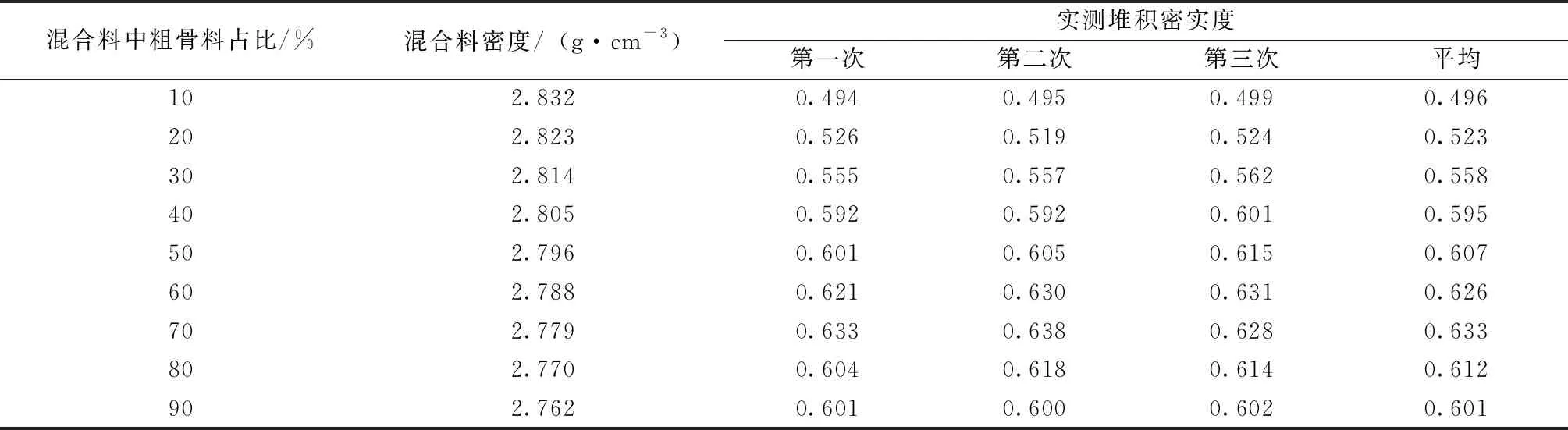
表2 废石-尾砂的堆积密实度实验结果Table 2 Experimental results of packing density of waste rock tailings
根据管道输送的要求,选择废尾比5∶5,6∶4,7∶3的三种混合骨料配制而成的充填料浆进行侧限压缩试验与压力泌水试验。
1.2 试验方案
1)侧限压缩试验
将装有充填料试样的环刀置于刚性护环中,在试样上下放置透水石是骨料受压后排出空隙水的两个界面,由于金属环刀及刚性护环的限制,使得充填骨料在竖向压力作用下只能发生竖向变形,而无侧向变形,又称侧限压缩试验,这与压力泌水仪以及管道的环境是一致的,试样产生的压缩量可通过百分表测量。一般规定每小时变形量不超过0.05 mm即认为变形已经稳定。本次试验采用的分级加荷载量p为:50、100、200、300、400、500、750、1 000、1 500,2 000 kPa。
2)压力泌水试验
对废尾充填膏体料浆进行不同压力下的压力泌水试验,选取试验压力为0.5、1、1.5、2 MPa;加压时间从0~200 s,选取10 s为时间间隔,实时记录试验数据,具体试验方案见表3。

表3 充填膏体料浆压力泌水试验方案Table 3 Pressure bleeding test scheme of filling paste slurry
1.3 试验结果与分析
1)侧限压缩试验
根据废石尾砂侧限压缩试验结果,绘制出废石尾砂e-p关系曲线,如图1所示。
从图1可以看出,在侧限压缩条件下,空隙比随压力的增大而减小,而且初始压缩阶段比后压缩阶段曲线较陡,逐渐平缓,说明开始压缩比较容易,随着空隙比的减小,充填骨料密实到一定程度后,骨料颗粒移动愈来愈困难,压缩量也随之减小。不同骨料比的充填骨料压缩曲线大致趋势基本相同,但初始空隙比越大的充填骨料加压初期空隙比减小得越快。所以压缩曲线上任意一点斜率a反映了在相应压力作用下充填骨料压缩性的高低,称为压缩系数。

图1 废石尾砂e-p关系曲线Fig.1 e-p curves of waste rock tailings
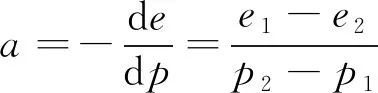
(1)
式中:a为压缩系数。
压缩系数能反映空隙比随着压应力的变化规律,从微观上来看,膏体拌合物压力泌水的本质是空隙比随着压应力的存在而减小,进而挤出膏体拌合物空隙中的水分,形成泌水效应。
2)压力泌水试验
泌水率是指泌水量与膏体拌合物含水量之比[16]。
(2)
式中:Vb为泌水量;Vw为充填膏体含水量。
通过压力泌水试验,在骨料比水泥添加量相同的情况下,得到充填膏体料浆压力泌水率与受压时间的关系曲线如图2(由于篇幅关系,以水泥添加量280 kg/m3,骨料比5∶5,质量浓度79%、80%为例)。
从图2各个图中可以看出,废石尾砂充填膏体料浆的泌水率随着加压时间的增长呈现出由急剧增长到缓慢增长最后趋于稳定的态势,泌水率的增长速率越来越缓慢,最终几乎保持水平,通过大量试验可以看出,充填膏体料浆在受压170 s以后,几乎不泌水,曲线几近水平。充填膏体料浆的压力泌水率随着压应力的增大而增大,压力泌水量与压应力呈正相关,随着压应力的增大,泌水率的增量越来越小,反映到图中就是泌水率-压应力关系曲线越来越平缓,这是因为,当开始受压应力作用时,充填膏体料浆内部粗细颗粒快速填充,空隙极具缩小,但继续加压时,由于之前内部颗粒之间的空隙已经缩小,即使再增大压力,空隙缩小幅度也会越来越低,当压力趋近无穷大时,泌水率-压应力关系曲线就会趋于水平,当充填料浆内部空隙趋近于完全闭合时,达到最大密实状态,即使再增大压力,泌水率也不会增加。
2 膏体压力泌水率计算模型的建立
泌水效应形成的本质即为充填膏体内部空隙在受压后缩小,从而排挤出空隙中的水分,从泌水形成的本质着手,建立充填膏体压力泌水效应的计算模型是可行的,由图1可知,充填膏体骨料e-p曲线随着压力p的逐步增大,空隙比e呈非线性不断减少,e-p割线斜率不断减少,当压力p为0或压力作用时间t为0时,空隙比为初始空隙比e0,当压力p或压力作用时间t趋向无穷大时,空隙比趋向于0。故充填膏体料浆压缩曲线应该满足如下四个条件:
(3)
式中:e0为充填骨料初始空隙比;e(p)为充填骨料在压应力p作用时间t的空隙比。
因此,根据式(3),可以建立充填骨料空隙比与压应力的关系表达式为:
e=e0·exp(-npt)
(4)
式中:n为应力参数。
因为充填料浆在压应力作用下泌水的本质是空隙比在压应力作用下而变小,从而挤出原来保存在空隙中的水,所以空隙在压力作用下缩小的体积,即为压力泌水体积,由此,式(4)可以变换成:
e0-e=e0-e0·exp(-npt)
(5)
即:e0-e=e0[1-exp(-npt)]
(6)
根据空隙比的定义,式(6)可变换为:
(7)
即:
Vb=Vse0[1-exp(-npt)]
(8)
再根据泌水率的定义,可以建立泌水率B与压力p的关系表达式为:
(9)
式中:B为压力泌水率;Vb为泌水量;Vw为膏体拌合物的含水量;A为材料参数,与初始空隙比e0与料浆配比参数相关,影响着最终压力泌水率。
利用Origin拟合软件,将新建泌水率计算模型与压力泌水试验结果进行拟合,拟合结果见图3。
对拟合结果进行F检验,检验结果见表4。
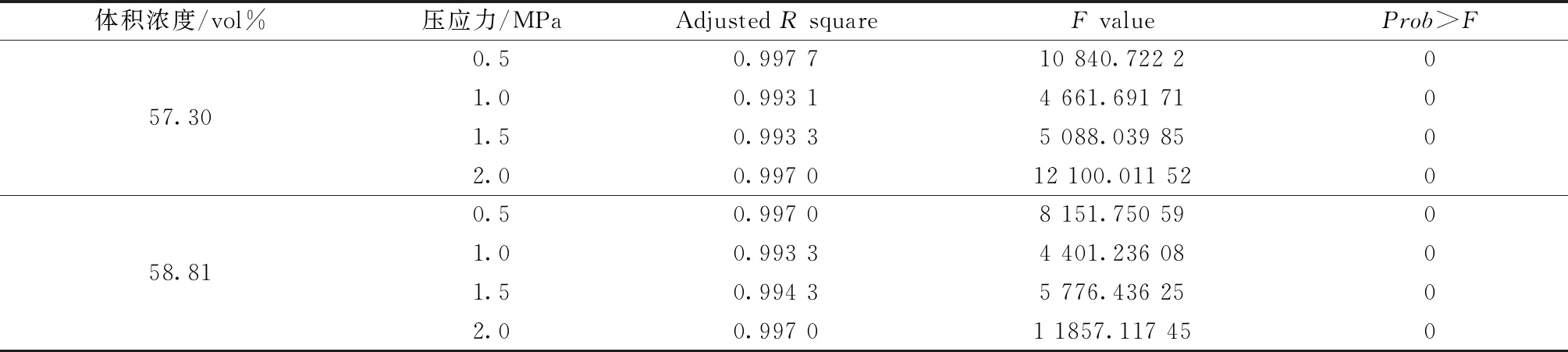
表4 拟合结果F检验表Table 4 Fitting result F inspection table
从图3及表4可以看出,该压力泌水率计算模型与压力泌水试验结果拟合程度较高,F检验方差分析显示:F>F0.995=5.36>F0.99=4.6,且Prob>F的值均小于0.05,属于高度显著,能够较好地反映出充填膏体料浆压力泌水率与压应力大小以及压力作用时间的变化关系,有一定的适用性。
3 材料参数A与应力参数n的确定
3.1 材料参数A的确定
从压力泌水试验曲线可以看出,材料参数A的意义是在某一压应力下的最大泌水率,即当压力泌水率趋近于A时,则泌水趋于稳定。由试验分析结果可以看出,当压应力一定时,材料参数A的值取决于充填膏体料浆的配合比参数,即初始空隙率ω0与充填膏体料浆的体积浓度Cv,对于材料参数A来说,由于其物理意义是某一压应力下的最大泌水率,所以应满足以下极限条件:
(10)
因此可以定义膏体最大泌水率参量Cv/ω0来表征材料参数A,最大泌水率参量Cv/ω0与材料参数A的关系散点图如图4所示。
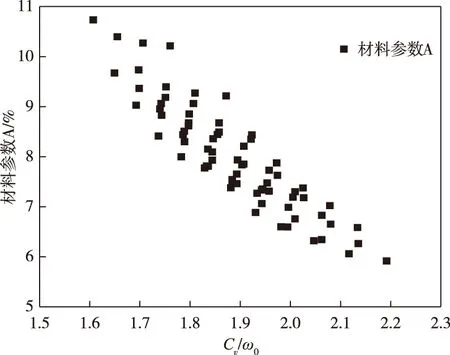
图4 材料参数A与Cv/ω0的关系散点图Fig.4 Scatter diagram of relationship between material parameter A and Cv/ω0
根据式(10)与图4所示,可定义材料参数A与体积浓度Cv、初始空隙率ω0的关系表达式为:
(11)
利用式(11)对材料参数A值进行拟合,以验证模型的可靠性,拟合结果见图5。
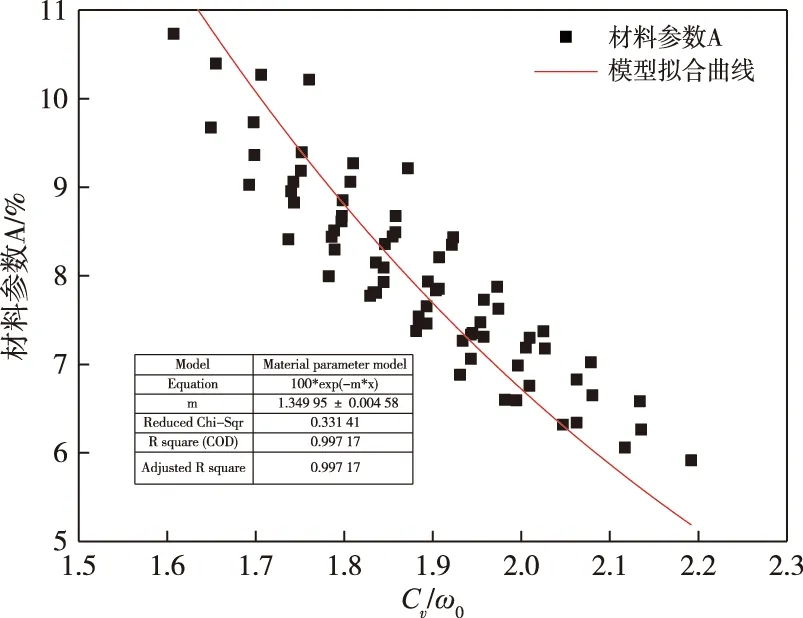
图5 材料参数A与Cv/ω0拟合曲线Fig.5 Fitting curve of material parameter A and Cv/ω0
从图5可以看出,该材料参数模型可以很好地反映材料参数A与体积浓度Cv和充填料初始空隙率ω0之间的关系。
3.2 应力参数n的确定
从压力泌水率计算模型及其拟合曲线可以看出,压应力参数n是关于压应力p及充填料初始空隙比的函数,影响着压力泌水曲线的弧度,当配比参数一定时,压力越大泌水速率越快,n值越小,泌水曲线就越陡。
根据充填料的侧限压缩试验结果,可以得知n是关于压应力p及充填料初始空隙比的函数,即:
n=f(p,e0)=ampm+am-1pm-1+am-2pm-2+…+a2p2+a1p+be0
(12)
式中:a为充填料压缩系数。可以求得充填料压缩系数的表达式为:
(13)
式中:c=a1/e0+b
1)当假设应力系数n与压力p满足线性关系时,即:
n=f(p,e0)=a1p+be0
(14)
此时,充填料压缩系数的表达式为:
(15)
2)当假设压应力系数n是压力p二次函数时,即:
n=f(p,ω0)=a2p2+a1p+be0
(16)
此时,充填料压缩系数的表达式为:
(17)
由式(14)~(17)可知,随着f(p,e0)函数方程次数的提高,充填料浆压缩系数a的精度越高,但增加了试验次数,以及充填料浆压缩系数非线性表达式的复杂程度,为此应该依据实际工程需求进行取值分析,以废石尾砂5∶5,水泥添加量为280 kg/m3的充填膏体料浆为例,其初始空隙率ω0为0.303,初始空隙比e0为0.435,其应力参数n与压应力p的关系散点图与不同方程次数的拟合结果见图6。
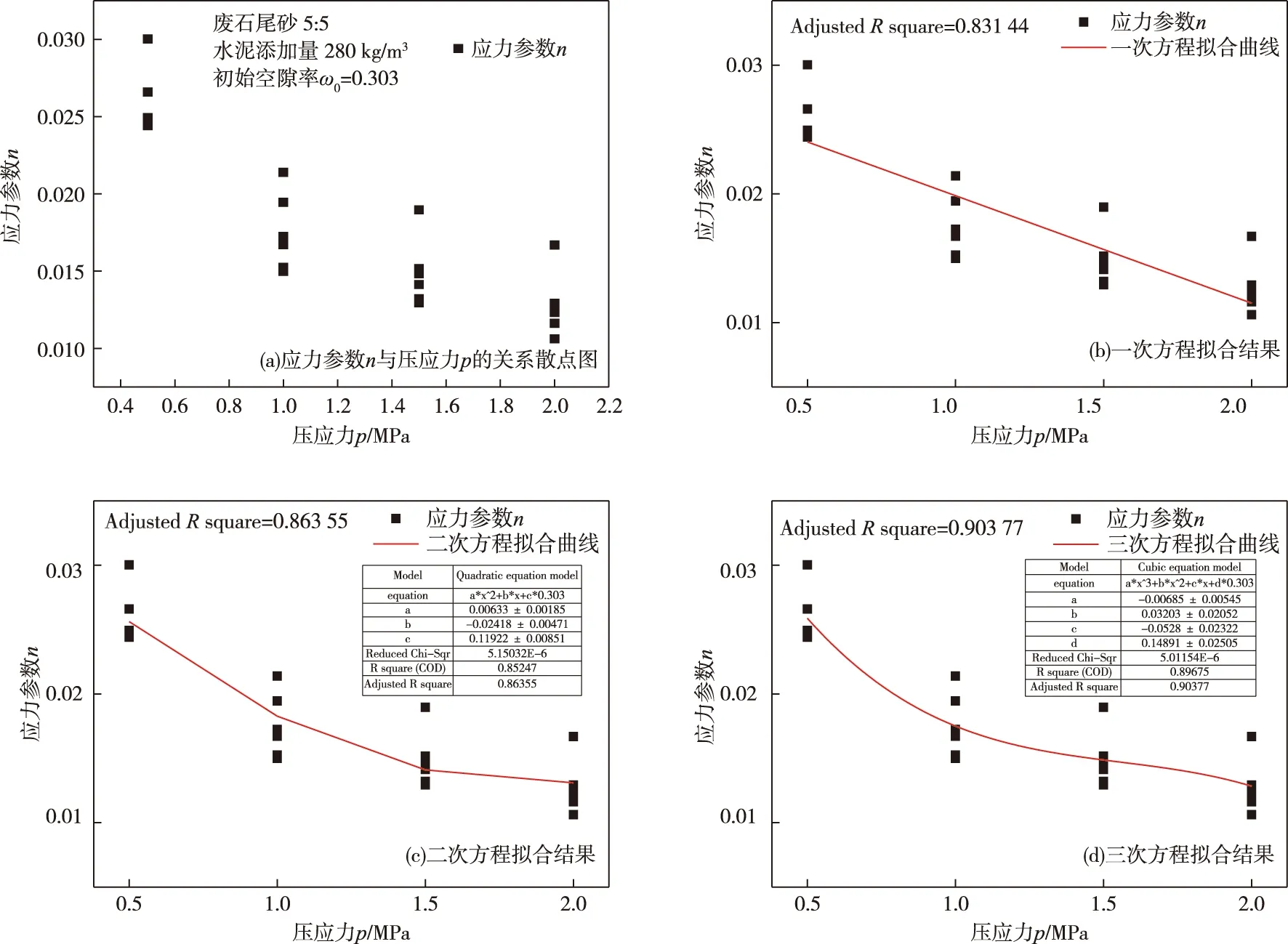
图6 应力参数n与压应力p多项式拟合结果Fig.6 Fitting results of stress parameter n and compressive stress p polynomials
从图6可以看出,拟合方程次数越高,拟合程度越好,精度越高,从拟合结果可以看出,该多项式可以较好地反映应力参数n与压应力p之间的关系,有一定的适用性。
综上所述,将式(11)与式(12)代入式(9)中,得到充填膏体料浆的压力泌水率计算模型为:
(18)
式中:B为充填膏体压力泌水率;Cv为充填膏体料浆的体积浓度;e0为充填膏体料浆的初始空隙比;p为充填膏体料浆所受压应力;t为压力作用时间;m为拟合参数。
4 膏体管输边界层厚度估算新模型
充填膏体在管道输送过程中,由于管压泌水效应的存在,泌出的水分会在管道边壁处形成一层润滑膜,该润滑膜即为管道输送的边界层,CHOI等[17]对水泥浆进行了环管实验,发现了明显的边界层效应,并利用UVP技术对浆体边界层的厚度以及速度分布进行了检测,结果表明:边界层厚度与流速无关;KALYON等[18]在此基础上,采用了不同的试验手段,进行了大量颗粒悬浮液滑移特性的研究,涉及浆体的固体填充率Cv/Cvm,覆盖范围为0.17~0.94,并得到基于浆体固体填充率的边界层厚度经验关系式。
根据膏体压力泌水效应,发现膏体管输过程中的边界层厚度不是一成不变的,因此,可以基于膏体拌合物的泌水效应,来估算膏体管道输送的边界层厚度。膏体在管道内泌水形成的边界层厚度示意图如图7所示。
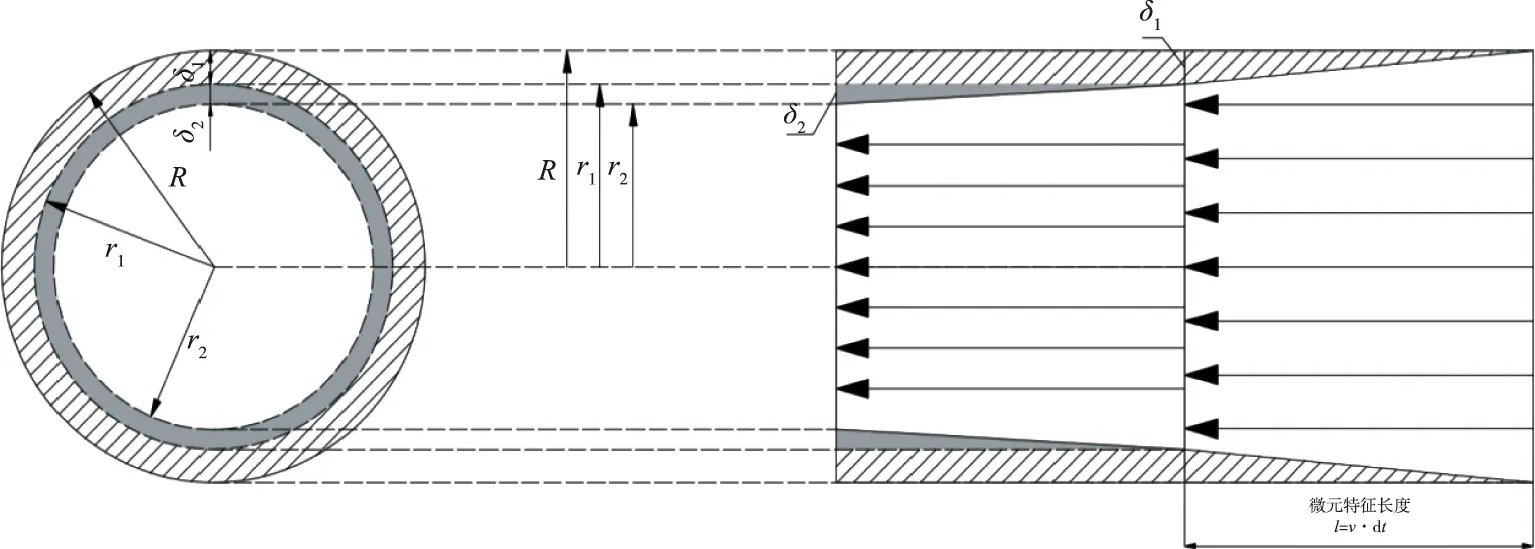
图7 膏体拌合物管压泌水边界层厚度示意图Fig.7 Schematic diagram of thickness of pipeline pressure bleeding boundary layer of paste mixture
从图7可以看出,膏体料浆在管道内形成边界层厚度不是一成不变的,随着泌水率变化而变化,由于泌水率会逐渐趋于稳定,即泌水率的增量越来越小,所以边界层厚度的增加趋势也会越来越缓慢,最后趋于稳定。取一长度为l的微元,微元长度为:
l=v·dt
(19)
式中:v为膏体拌合物管输速度。
微元内充填膏体料浆总体积为:
dV=πR2l=πR2vdt
(20)
微元内膏体拌合物泌水总量为:
dVw=dVCwB=CwπR2lB
(21)
式中:B为压力泌水率;Cw为水的体积比率。
从图7可以看出,管道微元内边界层液体体积为膏体总体积与流核区体积之差,流核区的体积为一圆台体积,因此,管道微元内边界层液体体积为:
(22)
化简得:
(23)
联立式(21)与式(23)得:
(24)
化简得:
(25)
由于边界层厚度极薄,远远小于管道半径,因此其与管道半径的比值趋近于0,所以Δδ2/3R趋近于0,可忽略不计,因此,边界层厚度随压力泌水率的变化率的关系为:
Δδ=CwBR
(26)
对式(26)求积分得:
(27)
式中:C为常数项,其意义为最终稳定时的边界层厚度,是与平均粒径和固体填充率相关的参数。可用下式计算:
(28)
式中:B为压力泌水率;Cw为水的体积比率;R为管道半径;dp为充填膏体的平均粒径;Cv为膏体拌合物的体积浓度;Φ为充填骨料堆积密实度;dp(1-Cv/Φ)为最终稳定时的边界层厚度。
部分配比的充填膏体拌合物管输边界层厚度函数曲线如图8所示。
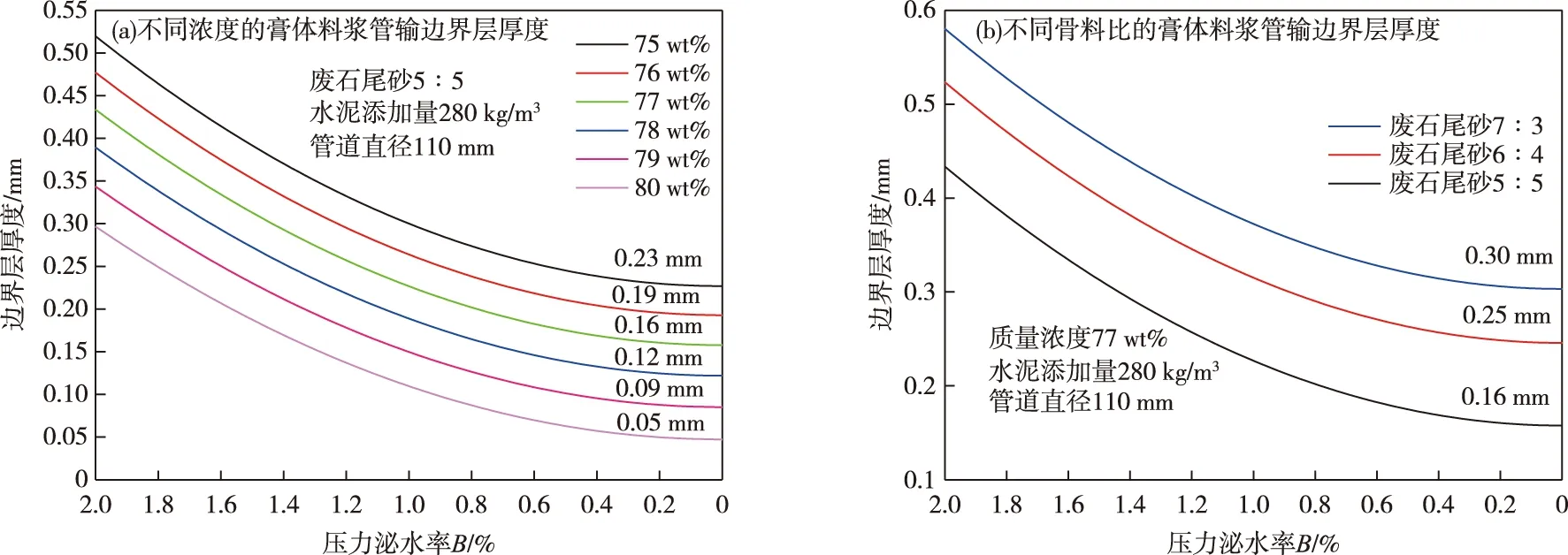
图8 边界层厚度估算公式函数图Fig.8 Function chart of boundary layer thickness estimation formula
从图8可以看出,边界层厚度随着压力泌水率的减小而逐渐趋于稳定,稳定时的边界层厚度则取决于膏体拌合物的体积浓度、密实度以及加权平均粒径;由于在管输过程中,沿程阻力损失的存在,管压是随着管输的进行而减小的,所以压力泌水率也是逐渐降低的,直至压力减小到不能泌出新的水分的程度,及压力泌水率减小到0时,边界层厚度也趋于稳定,所以,用式(27)来估算膏体拌合物管道输送过程中边界层厚度是合理可行的。
5 结论
1)膏体料浆的泌水率随着压应力和加压时间的增长呈现出由急剧增长到缓慢增长最后趋于稳定的态势,泌水率的增长速率越来越缓慢,最终几乎保持水平;并进行了充填料的侧限压缩试验,充填料浆压力泌水的本质是充填料内部空隙体积在受压后变小,从而将空隙水排挤出来。
2)分析了压应力、初始空隙率及水灰比对充填膏体料浆压力泌水效应的影响规律,并根据充填料浆的e-p曲线的变形规律,提出了充填膏体料浆压力泌水率的计算模型。
3)分析了材料参数的变化规律,材料参数的物理意义即为充填膏体料浆在某压应力下的最大泌水率,构建了充填膏体料浆最大泌水率影响因数Cv/ω0来表征充填膏体料浆在某压力下的最大泌水率,从而将级配参数引入到压泌水率计算模型中。
4)分析了应力参数随着应力和初始空隙率的演化规律,认为应力参数是一个关于压应力和初始空隙率的多项式函数,函数的次数越高,精度越高。
5)提出了基于压力泌水效应的膏体管输边界层厚度估算方法,认为膏体料浆在管道内形成边界层厚度不是一成不变的,随着管输的进行,边界层的厚度会逐渐趋于稳定,稳定后的边界层厚度由膏体体积浓度、密实度以及加权平均粒径共同决定。
