基于遗传算法与Dubins理论的高速无人系统在多障碍环境中的路径规划
2021-12-31郭继峰罗汝斌
李 艳,郭继峰,罗汝斌
(1.北京宇航系统工程研究所,北京 100074;2.哈尔滨工业大学航天学院,哈尔滨 150001)
1 引 言
美国国防部2018年8月发布了《2017—2042财年无人系统综合路线图》[1],对无人系统的发展提供了总体战略指南。在此路线图中,无人系统自主性作为4 个关键主题内容之一,是美军近年来对无人系统重点布局的发展方向。而无人系统自主导航是实现无人系统高度自主性的关键技术。无人系统自主导航包括4 个基本要求,即感知、定位、路径规划、运动控制,其中路径规划是最重要的部分之一。目前,无人系统的路径规划算法可以分为经典方法和启发式方法[2-3],如图1 所示。

图1 路径规划算法的基本分类Fig.1 Basic classification of path planning algorithms
目前,主要的经典方法包括单元分解法(Cell Decomposition Method,CD)、势场法(Potential Field Method,PFM)、基于采样的方法(Sampling- Based Method,SBP)和Dubins 算法。在CD 中,机器人配置的自由空间被划分为称为单元的小区域,目标是提供一条无碰撞路径,以到达目标。基于该方法的机器人路径规划应用见文献[4-5]。在PFM 中,障碍物和目标分别被赋予排斥力和吸引力,这样机器人就能够在远离障碍物的同时朝着目标移动[6]。为了解决动力学环境中的路径规划问题,文献[7]中引入了对经典PFM 的修改。SBP 算法的规划方案由于其在复杂的现实世界规划问题中的能力而受到相当大的关注。目前,应用最多的SBP 算法包括概率路线图(Probabilistic Route Map , PRM )和快速探索随机树(Rapid-exploration Random Tree,RRT)[8]。尽管连接随机采样点的概念在这两种方法中都是基本的,但这两种方法在构建连接点的方式上是不同的。文献[9]对SBP 的工作进行了全面调查。而RRT 因其计算效率和有效性以及相对快速地找到可行运动计划的能力而受到了相当多的关注,即使在高维空间中也有一定的应用[10]。上述方法把机器人当作质点,未考虑其自身的运动约束以及由于其最小转弯半径对于避障带来的影响,而Dubins 曲线是给定始末方向以及在转弯半径有约束的情况下两点之间的最短曲线,被广泛应用于自主机器人的路径规划中。文献[11]将Dubins算法应用到无人机的避障规划中,实现了无人机的实时避障规划。
然而,经典方法应用于实时运动规划时会有一定的缺陷,这些算法容易倾向于锁定在某些局部最优值中而忽略了全局最优路径。而且,它们中的一些可能无法在存在多个障碍物的环境中提供合适的解决方案。启发式方法解决了这一问题。
常用的启发式方法包括神经网络、模糊逻辑和自然启发法。神经网络由于具有非线性映射、学习能力和并行处理等优点,已成功地应用于机器人路径规划中[12-13]。在模糊逻辑算法中,机器人导航是基于一组if-then 规则。在文献[14-15]中,引入了基于模糊逻辑的不同方法来解决机器人路径规划问题。一些受生物学行为启发而广为人知的算法已成功地应用于机器人路径规划[16],如遗传算法[11-15,17]、粒子群优化[18]和蚁群优化[19]。其中,遗传算法是一种基于自然遗传学的优化工具,它利用了自然选择、交叉和变异等过程的优势,在解决组合优化问题上具有很大的潜力。
本文结合遗传算法与Dubins 理论,提出了求解高速无人系统在多障碍环境下的路径规划算法。本文首先分别介绍了传统遗传算法和Dubins理论,然后提出了基于遗传算法与Dubins 理论的路径规划算法,在算法设计中,对路径的编码方式做了深入的研究,使得其适合在多障碍场景中采用遗传算法求解满足高速无人系统运动约束的最优路径。
2 基本问题模型
2.1 遗传算法
遗传算法使用了群体搜索技术,将种群代表一组问题的解,通过对当前种群施加选择、交叉和变异等一系列遗传操作,产生新一代的种群,并逐步使种群进化到包含近似最优解的状态。遗传算法提供了一种求解复杂系统优化问题的通用框架,它不依赖于问题的具体领域,对问题的种类有很强的鲁棒性。该算法主要流程如图2 所示。

图2 遗传算法基本流程Fig.2 Basic process of genetic algorithm
2.2 Dubins 理论
Dubins 于1957年提出了Dubins 曲线理论,主要内容是在满足一定曲率条件下,连接同一平面内具有特定方向向量的任意两点的最短轨迹是曲线[20]。在没有其他约束因素的情况下,同一平面上的任意两点的最短路径是直线,但是在有一定的曲率约束的情况下,最短的路径则是圆弧。Dubins 曲线理论主要用来求解有曲率约束的最短路径。
通过选择两条与两个圆相切的切线中的一条,可以得到Dubins 路径,其中起始和终止位置都在圆弧上。圆弧的半径是曲率半径,它由无人系统的转弯半径决定,圆弧中心就是曲率中心,于是该问题就简化为寻找两个圆弧的公切线。两圆之间有两种公切线:内切线、外切线。
在给定位姿点下,无人系统可以向左转和向右转,路径可以以顺时针方向和逆时针方向结束。一个给定的位姿点上有两种转弯方式,因此有两个相切圆,如图3 所示。一个向右转弯,在弧段 1C上标记R,另一个是向左转弯,在弧段 2C上标记L,一个位姿点可以产生4 条Dubins 路径。即LSL,LSR,RSL,RSR, 如图4 所示。

图3 相切圆Fig.3 Tangent circles
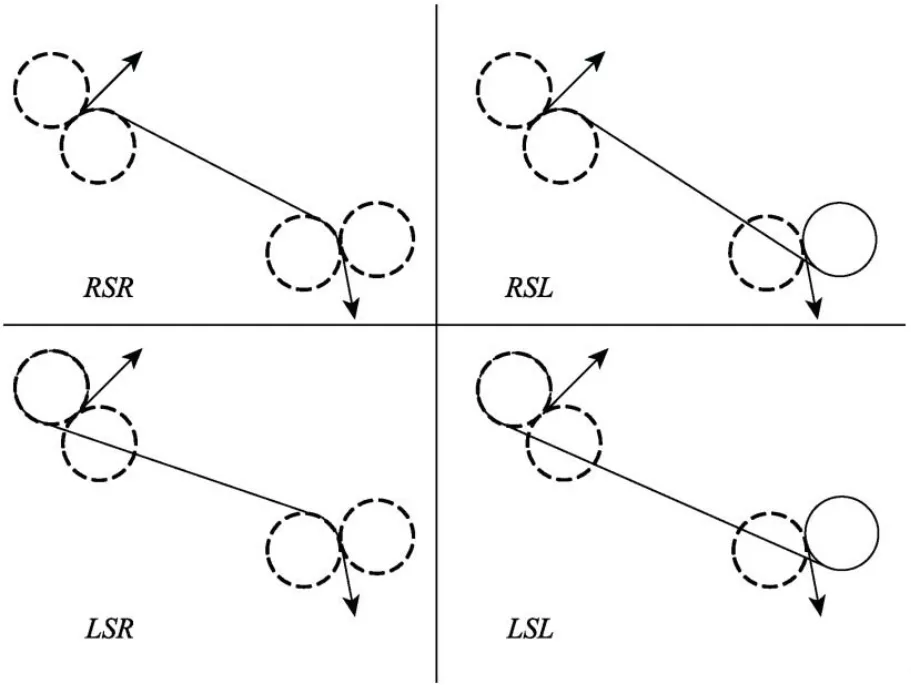
图4 4 种Dubins 路径Fig.4 Four Dubins paths
无人系统路径规划问题是指在已知环境下,给定起点和终点,使无人系统在一定的优化目标下无碰撞地由起点飞到终点。在这种情况下,障碍的位置和大小是已知的,无人系统的性能是已知的。在本文中,最优目标是使无人系统的飞行路径最短。本文主要考虑的约束条件是无人系统的最小转弯半径。
3 基于遗传算法与Dubins 理论的路径规划算法
本文提出基于遗传算法和Dubins 原理的高速无人系统路径规划方法。其中,遗传算法用于求解最优路径,Dubins 原理用于满足无人系统的约束条件。遗传算法可以解决多障碍环境下的路径规划问题,但其规划出的路径没有考虑无人系统最小转弯半径这一约束条件,大多数都是不可飞路径;基于Dubins 理论的路径规划算法考虑了无人系统最小转弯半径的约束,求解得到的路径为可飞路径,并且还使得到达终点的速度方向可控,具有很高的实用性,但不能解决多障碍环境下的路径规划问题。将两者结合可得到一种有效解决多障碍环境下路径规划问题的方法,此方法使得规划出的路径平滑可飞,终点速度方向可控,其难点在于对路径的编码上,本文提出了一种针对障碍物的编码方式,有效地解决了上述问题。
3.1 针对障碍物的路径编码方式
在已知无人系统出发点Ps(xs,ys)、初始速度方向vs,终点Pf(xf,yf)、终点速度向量vf,最小转弯半径R和障碍圆模型Dk(k=1,2,…,n)的位置和大小的情况下,所求的路径是一条至少与l(l∈ [ 0,n])个障碍圆相切的曲线。则问题转化为求最短路径(Cs,Cf)=(Cs,W,Cf)的问题,其中W是该路径遍历的各个障碍圆序列组成的集合,其中有l个障碍圆与路径相切。编码方式要包含W中的所有可能,一种可行的编码方式是采用冗余二进制编码的方式[11]。假设有4 个障碍物,若要表示所有的情况则至少需要3 位二进制编码。编码方式如表1 所示。

表1 遗传算法编码表1Table 1 Genetic algorithm coding table1
利用上述编码方式,可表示的一种路径的编码方式是(001, 100, 011, 111),其表示的路径序列为(D2, Blank,D4, Blank),则这种序列得出的路 径为(Cs,D2,D4,Cf),表示由起始点出发,先与第2 个障碍圆相切,再与第4 个障碍圆相切最后到达终点。这种编码方式只是给出了路径遍历障碍圆的顺序,并没有给出与障碍圆相切的方式,即这种编码方式给出的路径不唯一。为了使得到的路径唯一,本文将有向曲线与圆的相切方式也加入到编码方式中。
所有操作都在超净实验室内完成,室温25 °C。采用Baseline抛光液,其成分为:20%(质量分数)硅溶胶,5%(体积分数)FAOI螯合剂(河北工业大学自主研发,含有多羧基多胺基,具备13个以上螯合环),0.05%(体积分数)双氧水。所用表面活性剂分别为弱碱性的FAOA和AEO(其分子结构见图1,R表示12个碳的链状烷基,n为常数)。
考虑到有向曲线与圆的相切方式时,路径的编码方式将发生变化。每一个圆都有两种情况,圆在切线左边或者圆在切线右边,在编码时每个圆就有两种编码方式分别代表以上两种情况。根据以上方法对上述4 个障碍圆编码,总共有12 种情况,需要4 位二进制编码。编码方式如表2 所示。
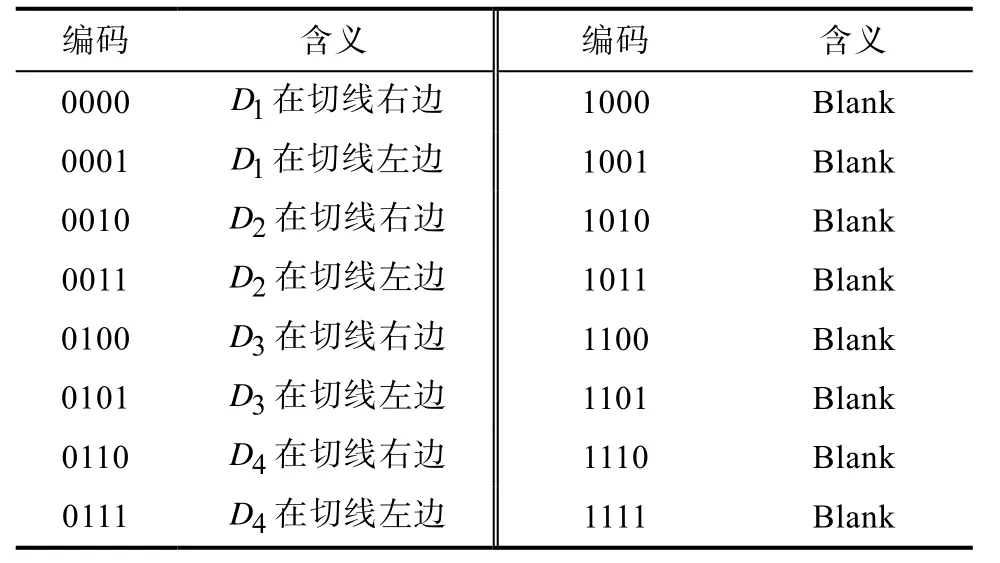
表2 遗传算法编码表2Table 2 Genetic algorithm coding table2
根据上述编码,可表示的一条路径是(0000, 0100,1111,0111),即路径序列为(D1,D3,Blank,D4),其表示的路径如图5 所示。以上编码的路径只能保证路径不与障碍物D1,D3与D4发生碰撞,并不能保证不与其他障碍物发生碰撞。在适应度函数的设计中,通过增加碰撞检测解决这一问题。
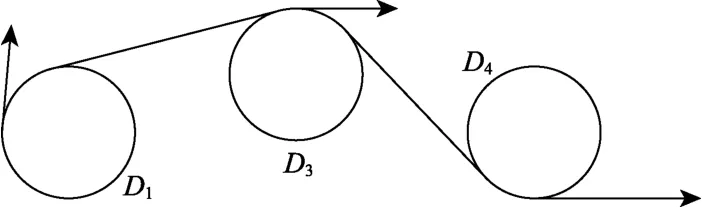
图5 障碍圆之间的Dubins 路径Fig.5 Dubins paths between obstacle circles
3.2 适应度函数
本文所规划的路径是由起点到终点的无碰撞最短路径。所以,适应度函数应该能满足无碰撞和最短这两个条件。本文采用路径长度的倒数作为目标函数,在计算路径长度时,若当前路径与障碍物相交,则将当前路径的长度给一个较大值,以保证所求路径与障碍物不相交。所设计的遗传算法适应度函数为

式中,L为路径的长度;K为调节系数,其主要是因为L的值远大于1,所以求得的适应度函数值非常小,不利于种群的进化,所以乘以一个与L同量级的数调节适应度函数的值,保证种群的正常进化。
4 仿真验证
4.1 飞行环境建模
在高速无人系统执行任务的过程中,将会面临敌方的探测雷达、拦截导弹、电子干扰等威胁,这些威胁的作用范围一般为不规则的几何形状。在本文研究中,为了统一威胁障碍建模,方便计算,将高速无人系统可能遇到的威胁障碍抽象为圆形模型,即威胁障碍是以其中心点为圆心的圆形区域,此圆形区域是包络威胁障碍的最小圆形区域。同时,考虑到无人系统自身的体积大小以及导航制导控制系统带来的误差,直接在上述圆形障碍物基础上进行避障将有一定的风险。基于安全性考虑,我们在障碍物的大小上增加距离为ΔRs的安全距离,在增加安全距离之后,障碍物的作用半径将增加至Rs(i)=R(i) +ΔRs。安全距离ΔRs的取值可根据无人系统的体积大小,飞行速度,导航制导控制系统误差等因素综合考虑。综上所述,经过飞行环境建模之后的威胁区域半径RD为:
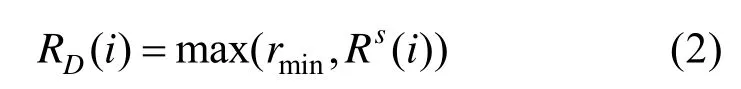
式中,RD(i)为考虑高速无人系统最小转弯半径之后的第i个威胁障碍区域的半径;rmin为无人系统的最小转弯半径;R(i)为包络第i个威胁障碍区域的最小圆的半径。表3 所示为一个考虑了多种威胁的飞行环境,最小转弯半径取值为rmin=173 km,安全距离取值为ΔRs=20 km。

表3 考虑多种威胁的飞行环境建模Table 3 Modeling the flight environment under multiple threats
假设飞行器的起点为(0, 500) km,终点为(3000, 1000) km,根据上述步骤构建的飞行环境如图6 所示。其中,红色多边形填充区域为各威胁的实际形状,红色实线圆表示包围实际威胁区域的最小包络圆,粉色点线表示考虑无人系统最小转弯半径之后的威胁圆,绿色虚线圆为增加安全距离之后的威胁圆。

图6 包含多种威胁的飞行环境Fig.6 A flight environment with multiple threats
4.2 无人系统最小转弯半径

根据上述方程,可以得到无人系统的最小转弯半径rmin为:

式中,g为重力加速度。
4.3 仿真结果
我们使用第3 节提出的算法,在4.1 节描述的飞行环境中规划无人系统从起始状态到终止状态的路径。所求飞行环境中,共有11 个障碍物,每个障碍物需要6 个二进制编码表示,所以共需66 位二进制编码才能表示一条路径。初始种群大小设置为500,最大进化代数为50,交配概率为0.95,变异概率为0.1,选择步骤选用轮盘赌选择方式,交叉步骤选用单点交叉方式,变异步骤选用基本位变异方式。适应度函数中参数K的值设为1000 km。假设无人系统的飞行速度为1 km/s,最大滚转角为30°,根据式(4)可求得无人系统的最小转弯半径为173 km。我们将本文提出的算法与两个传统算法进行对比,即A*算法[21]与基于Dubins 曲线修正的A*算法[22]。A*算法是一种常用的路径搜索算法,用于在离散环境中搜索从起点到终点的最优路径,但其搜索出的路径由折线段构成,路径连接处不满足无人系统的运动约束条件,故不能单独用于具有运动约束的无人系统路径规划中。基于Dubins 曲线修正的A*算法对A*算法搜索出的路径进行了平滑处理,使路径连接处满足无人系统的运动约束,使其可用于实际应用。
4.3.1 静态环境仿真
在上述静态环境中,进行了算法性能的对比实验。对于每一种算法,在上述飞行环境中进行了100 次随机实验,在每次实验中,固定障碍物不变,随机选取无人系统的初始状态以及终点状态,计算规划路径的长度。各算法性能对比结果如表4 所示。

表4 路径规划算法性能对比结果Table 4 Path planning algorithm performance comparison results
由表4 可知,A*算法规划的路径最短,使用Dubins 曲线修正的A*算法规划的路径最长,基于遗传算法与Dubins 曲线规划方法规划出的路径长度在两者之间。A*算法能够规划出最短的路径是因为其不考虑无人系统的运动约束,规划出的路径是由直线段连接而成的,无法满足无人系统的最小转弯半径,不可实际应用于高速无人系统的路径规划中。使用Dubins 曲线修正的A*算法规划的路径最长,是由于其直接在A*规划的路径上进行了修正,无法充分利用飞行环境的特征,只能求得次优解。而基于遗传算法与Dubins 曲线的规划方法从全局考虑,结合无人系统的约束条件与飞行环境,将可行路径进行编码,使用遗传算法进行搜索求解,理论上在足够大的种群规模与迭代次数下,可以搜索得到最优解。一般规模的问题无须设置大规模种群与高迭代次数即可求解到最优解。通过以上性能对比实验结果分析可知,本文提出的算法可得到满足无人系统运动约束以及初始状态与终止状态约束的最短路径。
以下仿真实例直观地展示了各种规划算法的特点。仿真实验设置为:无人系统初始位置为(0, 500) km,初始速度为(1, 0) km/s,目标位置为(3000, 1000) km,目标速度为(0, -1) km/s,飞行环境中各威胁障碍均为静止状态。仿真结果如图7 所示。
图7(a)所示为在上述飞行环境中各算法所规划出的路径。蓝色实线为本文提出的基于遗传算法与Dubins 曲线规划方法规划出的路径,路径总长为3460.5 km,路径与3 个障碍圆相切,同时在初始点与目标点处生成最小转弯半径圆,路径与起始圆以及终止圆相切,满足速度矢量约束。深绿色实线为A*算法规划出的路径,路径长度为3369.4 km。可以看出,虽然A*算法可以规划出更短的路径,但路径由多条折线段构成,在路径连接处不够平滑,无法满足无人系统的运动约束,且在终点处没有满足速度矢量约束,故不能实际应用。黄色实线为在A*算法规划的路径基础上经过Dubins 曲线修正后的路径。经过Dubins 曲线的修正,路径连接处由满足无人系统运动约束的圆弧连接,且在终点处通过圆弧连接直线路径,使规划出的路径满足终点速度矢量约束。通过以上修正过程,路径长度增加到4208.1 km,长于基于遗传算法与Dubins 曲线规划方法规划出的路径长度。
图7(b)所示为基于遗传算法与Dubins 曲线规划方法的迭代求解过程。曲线所示为种群的适应度函数值变化情况。由图中结果可知,种群的最大适应度与平均适应度在不断增大,表明种群朝着有利的方向进化,所求得的路径逐步变短,最 后收敛到最短路径。

图7 静态环境仿真结果Fig.7 Static environment simulation results
4.3.2 动态环境仿真
我们使用一次典型的仿真实验说明本文所提算法的动态避障过程。仿真场景设置为:无人系 统初始位置为(0, 500) km,初始速度为(1, 0) km/s,目标位置为(3000, 1000) km,目标速度为(0, -1) km/s,飞行环境中探测雷达-2 向y轴正向按照0.2 km/s 的速度运动。仿真结果如图8 所示。
图8 展示了基于遗传算法与Dubins 曲线规划方法在动态环境中的避障过程。在t=0 s 时,首先规划出一条从起始点到终点的路径,与图8 所示结果一致。随着无人系统以及移动探测雷达-2 的持续运动,无人系统持续更新路径,在t=700 s 时规划的路径如图8(b)所示,可见由于探测雷达-2 的移动,无人系统在之前的路径上重新规划了新的路径。图8(c)所示为在t=1010 s 时规划的路径,此时无人系统仍然具有被探测雷达-2 发现的风险,因此规划的路径与其威胁圆相切。随着无人系统的运动以及探 测雷达-2 的运动,无人系统躲避开探测雷达-2 的探测威胁,在t=1560 s 时规划的路径如图8(d)所示。根据以上仿真实例结果,说明基于遗传算法与Dubins 曲线的规划方法可应用于动态环境中。

图8 动态环境仿真结果Fig.8 Dynamic environment simulation results
在实际应用中,一个关键问题是算法的实时性问题。而本文所提方法的复杂度与环境中的障碍物个数直接相关,其直接影响表示路径所需的二进制位数,障碍物越多,路径编码越长,运算时间也越长。为此,以下测试障碍物个数对算法实时性的影响。使用的测试平台为笔记本电脑,其CPU 具有4 个核心,基频为2.1 GHz。种群大小设置为500,最大进化代数为50。仿真结果如图9 所示。从结果中可以看到,当障碍物个数小于20 时,程序运行时间小于1 s,当障碍物个数等于30 时,程序运行时间为1.8992 s。考虑到高速无人系统的运动速度为km/s 级。因此,若能提前在数十公里外发现威胁障碍,则无人系统具有充足的时间进行规划,满足规划实时性需求。

图9 算法运行时间测试结果Fig.9 Algorithm running time test results
5 结 论
本文结合遗传算法与Dubins 理论,提出了求解高速无人系统在多障碍环境下的路径规划算法。所提算法使用遗传算法搜索最短路径,Dubins 曲线满足无人系统的约束条件。在算法设计中,对路径的编码方式做了深入的研究,使得其适合采用遗传算法求解。由仿真结果可见,所提算法可在多障碍环境中求得最短且平滑可飞的路径。 本文在求解最优路径时,假定无人系统在二维平面内运动,没有考虑在三维空间运动的情景,后续将进一步研究求解三维空间中满足无人系统约束的最优路径的方法。
