混沌算法在电力控制系统中的应用
2021-12-31国能长源电力股份有限公司
国能长源电力股份有限公司 翁 晓
随着时代的进步,互联网技术飞速发展,各个领域内应用到了自动化控制。尤其是电气自动化技术的发展突飞猛进,技术的发展催生了很多电气自动化设备,设备的应用非常广泛。针对电气自动化设备的应用设计的电力控制系统也逐渐完善,在电力控制系统内部出现差异或造成系统的不稳定性,因此,在进行电力控制系统设计的时候需要对设计的每个步骤都进行严格的把关,以保证电力设备可以被电力控制系统进行有效的控制,系统的整体性可以得到充分发挥。对系统进行优化可以增加系统控制的精确性。保证电能在输送的过程中不出现意外,实现电能的输送安全,并减少电能输送的消耗量。
PID 控制器是在电力控制系统中经常使用到的控制器,PID 控制器需要在使用之前进行参数的设定,参数设定的科学性决定了系统运行的效果。因此在控制系统的优化当中,PID 控制器的参数优化控制效果,能够决定整个控制系统的能力,对PID控制器进行合理有效的设定,能够对电力控制系统安全性能进行保障。所以对PID 控制器参数进行制约成为了电力控制系统保障输电安全的一种手段。PID 控制器自动化控制是建立在系统完善运转的基础上,参数的优化可以依赖于求解并优化工程中的参数设置函数。将控制参数的设置转变为函数的计算。通过相关的计算公式构建数学模型,用模型求解出参数的优化,以此实现电力控制系统的优化。
传统优化方式相比较建立数学模型的方式更繁琐,且无法保障控制的基本偏差。考虑对象对于参数的要求且选择的算法需要通过长时间的训练和学习才能符合控制的精度。优化使用的算法就是优化设计技术,混沌算法可以节省过渡性计算,设计控制系统和设置设备参数中也可以使用混沌算法。传统的电气控制往往需要工作经验丰富的技术人员进行专业的测算,保证不同的电力控制系统可以与不同型号的PID 控制器匹配。经验不足的人员会因为参数设定的难度加大而变得不知所措,通过混沌算法优化PID 控制器参数调整可降低系统操作难度。
1 基于混沌算法进行控制系统参数的优化
基于混沌自身规律,对控制系统参数进行优化,可以提升最优解的获得效率。将系统的参数进行划分,依赖混沌变量的变化对搜索变量进行调整,混沌算法可以提升电子系统参数选择的效率。尤其对于数据规模较小的系统来说,算法的加入效率提升很明显。但对于数据规模较大的系统来说,需要优化电力控制系统的参数。但可以通过缩短最优解的搜索时间的方法降低提升效率的难度。但无论哪种方法,都与遍历性有很大关系。
遍历性是指在一定的范围内经历该范围时算法的变换状态。这种状态的变化是有规律可循的,基于该算法的遍历性,在对电器系统进行优化设计中,通过完全搜索和混沌搜索法的运算,可以排除系统中的最小值,以此来优化传统搜索方式中适应性差的问题。通过对混沌映射函数的计算,利用数学建模的方式成功的解决控制系统参数的优化问题,将函数普通变量变为混沌变量,在算法中基于混沌算法的直接搜索,增加了系统参数选择的科学性。
2 基于混沌算法进行控制系统最优解的选择
在参数优化之后,通过混沌算法算出最优解,以便实现电力控制系统的有效控制。搜索混沌变量已经通过遍历性实现了优化,比起传统的电气系统中的随机参数搜索历时更短。混沌算法最优解的选择共分为两个阶段,首先将p(a)函数进行迭代映射,混沌变量会在轨道上进行最优解搜索,针对电气系统的最优解目标进行特征分析,此时属于最优解的初级搜索,搜索得到的状态仅仅处于满足终止搜索条件的地步。电力控制系统中的控制器的结构相对来说并不复杂,混沌算法对环境的适应力也很强,在第一步调整的参数较少。
如图1所示,设置足够的搜索时间就一定可以找到控制的解答最优化方案。求解最优解以第一部分的最优参数作为起点,利用混沌算法进行局部细节的搜索。算法按照准则完成计算并显示已经按照完成条件完成搜索,混沌变量本身也完成了附加扰动。调节控制器的自适应系数,将转入输入的控制信号设置为rk,则系统的控制过程为rk=b(k)-b1(k),式中k 代表混沌参数的系数,取值范围为k>0,控制信号是由混沌算法的关联搜索结果转换而来的,由于该算法的自适应能力很强,因此在k 的调整过程中加上图1中的HBBE 学习规则,增加控制系统的控制精度。
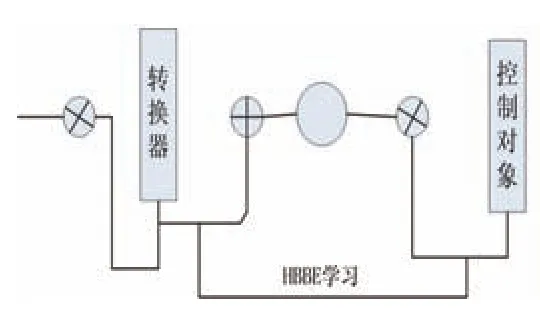
图1 基于混沌算法的电力控制系统结构
3 仿真实验
为了验证混沌算法在电力控制系统中的应用效果,设计仿真对比实验,采用本文设计的电力控制方法与向传统的故障预测电力控制方法、动态属性智能权重电力控制方法进行比较,比较三种方法的控制精度。
3.1 实验准备
采用混沌算法对电力系统进行故障恢复分析,首先对系统进行负载编码,将备用供电路径进行编码,采用三值化编码的方式,1代表该线路为正常状态,可以进行正常的供电,0代表该电路没有进行供电,处于无电状态。2代表该电路此时没有进行供电,但是正常的供电电路,通常情况下为备用电路。对供电电路进行编码,先对0和1两种非备用线路进行编码,分为非正常负载编码和正常负载编码。将混沌数值编码进行初始化处理。使用Tent 混沌映射方法,其初始化的公式为:
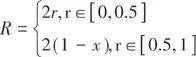
其中初始值的R 的取值为0~1且是随机进行抽取,x 为系数,r 为混沌量。实验中混沌算法的推理规则如表1。采用混沌算法进行预测在单位时间内某支路出现短路故障的可能性,停用某个支路并进行线路的更新和维护,以便重新进行供电方案的制定。供电恢复的示意图如图2。对故障点进行维修之后,电路恢复方案按照混沌算法的应用流程进行。
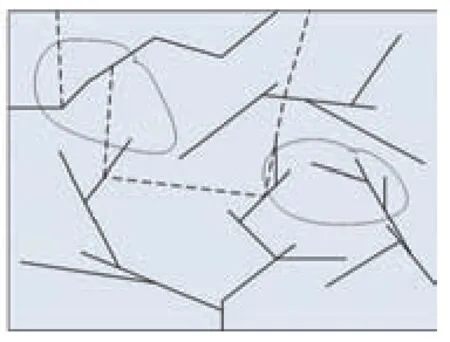
图2 电路恢复方案示意图
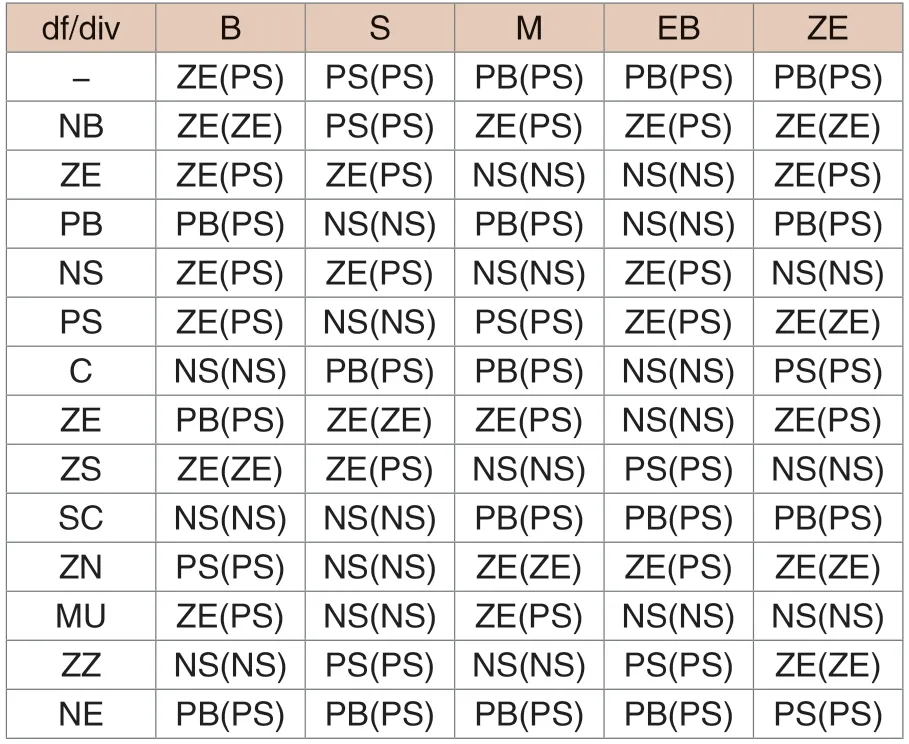
表1 混沌变量的推理规则
3.2 仿真结果与分析
经过四次迭代结果,发现只需四次就能实现最优解的选择,同时可以保证系统的稳定性。结果采用向量表示,为(1,1,0,2,1,1,2,1,2,2,0,0,1,0,1,2,1,2,1,2,0,0,0)。将本文方法与另两种现有控制方法进行对比,对比结果如表2所示。由此可知,使用本文设计的方法进行供电恢复,线路在恢复的时候采用的开关次数只有5次,开关的次数越少供电恢复的速度越快,开关次数越多同时需要改变供电路径的负载也更多。
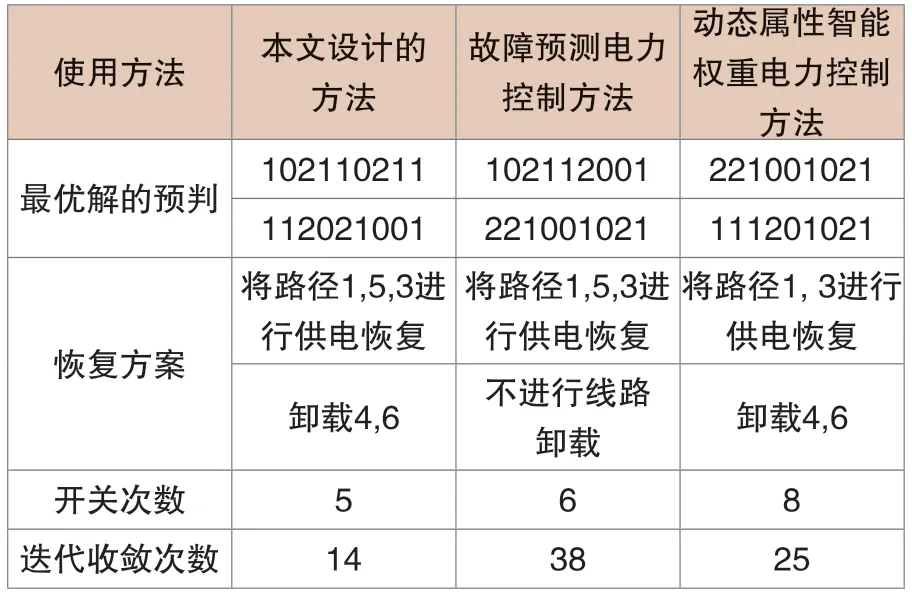
表2 实验结果
综上,本文将混沌算法与电力控制系统相结合,与传统的电力控制系统相比控制的效率提升了。但由于本文缺乏相关的时间数据,因此提出的方法过于理想化,希望在日后的研究中可以进行实践性的分析,增加电力控制系统优化的数据支撑。
