加载龄期对混凝土徐变的影响机理

2021-12-30孟华敏李辉周健徐名凤王少江

新型建筑材料 2021年12期

孟华敏，李辉，周健，徐名凤，王少江

（1.河北工业大学土木与交通学院，天津 300401；2.中国水利水电科学研究院，北京 100038）

0 引言

在荷载长期作用下，混凝土除发生弹性变形外，还会随着时间发生缓慢变形，即徐变[1]。徐变特性会对混凝土结构的应力分布产生很大的影响，例如徐变会引起预应力混凝土的预应力损失，增加大跨度梁的挠度等[2]。

自1907年美国材料学会首次报道了钢筋混凝土梁的徐变现象，人们逐渐开始对徐变进行研究。一般认为，影响混凝土徐变的因素有混凝土原材料及其配合比、加载龄期、应力水平、相对湿度、环境温度等[3-5]。目前提出的徐变机理主要有粘性剪切理论、塑性理论、渗出理论、微裂缝理论以及微预应力固结理论等[6-7]。粘性剪切理论认为混凝土徐变是由水化硅酸钙之间的剪切滑移引起的，这个过程是不可逆的，无法解释混凝土的可恢复徐变。塑性理论将混凝土徐变归因于晶体沿晶格的二维平面滑动的结果，这类比于金属的塑性变形，金属的塑性变形是不会发生体积变形的，而混凝土的徐变会导致其体积减小。微裂缝理论认为徐变是由裂缝的不断产生和发展而引起的，但该过程是不可逆的，无法解释混凝土的可恢复徐变。渗出理论认为徐变是由混凝土中含水量的变化引起的，凝胶水在荷载作用下逐渐被挤出而产生变形，Young[8]的研究表明，密封试件尽管没有水分损失也会产生徐变，这与渗出理论不相符。微预应力-固结理论是基于热动力学提出的，其中，微预应力理论主要研究了温度和湿度对徐变的影响，固结理论则侧重于水泥水化对混凝土徐变的影响，微预应力仅是一个假想的概念，还未得到试验验证[9]。但以上这些理论都只能说明徐变的部分机理，由于混凝土的徐变非常复杂，目前没有一种徐变理论可以解释所有的徐变现象[9]。

水泥的水化产物包括氢氧化钙（CH）和钙矾石（AFt）等晶体以及水化硅酸钙凝胶（C-S-H）等胶体。其中，水化产物的形成是水化过程中自由水溶液内的离子结晶的结果，而当有压力作用在水化产物上时，水化产物会发生溶解-扩散-重结晶[10]，从而使得水化产物发生不可逆的形貌变化。在混凝土的加载过程中，外力会作用在水化产物上，使其产生不可逆的溶解和重结晶，导致混凝土变形量的增加从而产生徐变。基于水化产物的溶解-扩散-重结晶的现象，可以充分解释压力、温度、湿度以及加载龄期等因素随混凝土徐变的影响。

加载龄期是影响水泥石水化最主要的因素之一，且加载龄期是影响混凝土徐变最主要的外部因素之一。为进一步研究加载龄期对混凝土徐变特性的影响，本文基于水化产物的热动力学，提出水化产物迁移理论，建立相对应的数值计算方法，再通过不同加载龄期的徐变试验来进行验证。

1 水化产物迁移理论

在宏观和细观尺度下，混凝土由粗细骨料以及水泥石基体组成。在微观尺度下，水泥石则是由C-S-H、CH、AFt和未水化的水泥颗粒等组成。在荷载作用下，水化产物会发生溶解，由于晶体的溶解速率远大于胶体的溶解速率[11]，故仅考虑晶体的溶解对混凝土徐变的影响。为便于分析，将水泥石中除孔和晶体之外的其他组分看作均质基体，构成如图1所示的基本单元，即基体-孔-晶体单元，以研究晶体溶解-扩散-重结晶过程对基体徐变的影响，基于此提出水化产物迁移理论。

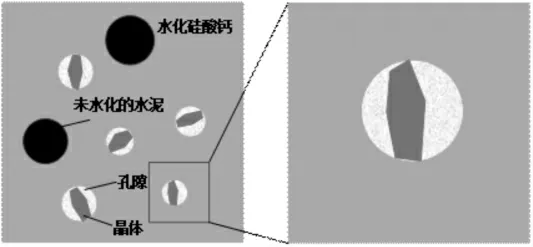
图1 水泥石的微观结构

基体受到外应力作用的同时，孔也会随基体变形而发生变形，此时晶体由于抑制孔变形也会受到压力的作用，如图2所示。压应力会提高晶体的化学势，此时晶体的化学势为：

式中：μc——受压晶体的化学势，J；

μ0——最初晶体与溶液的化学势，J；

σ0——作用在晶体上的应力，Pa；

vm——晶体的摩尔体积，m3/mol。

此时，晶体与其周围的溶液存在化学势差△μ1：

晶体和溶液之间的化学势差驱使晶体溶解至溶液中，随着晶体的不断溶解，与受压晶体相接触的溶液和其他区域的溶液之间存在浓度差。在浓度差的驱使下，与受压晶体相接触溶液中的离子会向其他区域扩散。当晶体扩散至其他区域时，晶体的溶解度恢复到最初值，此时溶液处于过饱和状态，在过饱和度的驱使下，晶体发生重结晶。晶体的溶解-扩散-重结晶过程造成了基体的变形。水化产物迁移理论示意见图2。

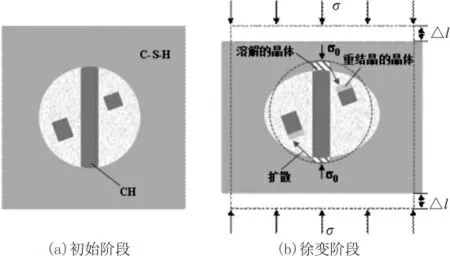
图2 水化产物迁移理论示意

有研究指出[10]，基体的变形与晶体的溶解相关。假设水化产物迁移理论中的溶解过程速率小于扩散和重结晶速率，则溶解速率控制整个变形速率。晶体的溶解量与溶解的驱动力成正比[12]，则晶体的溶解量为：

式中：R——气体常数，通常Rg=8.314 J/K；

T——温度，K；

jdis——晶体的溶解量，mol/（m2·s）；

kdis——在驱使力为1 RT下的溶解速率，mol/（m2·s），其中，CH的溶解速率为（2.2±1.3）×10-5mol/（m2·s）[13]。

晶体溶解速率为：

因此，晶体的溶解时间，即徐变时间为：

由式（5）可知，只要得到一定长度下晶体所受的应力即可求得溶解一定量晶体所需的时间，若再求得一定溶解长度下基体的应变，则可得到基体徐变随时间的变化规律。由于徐变是一个应力-应变关系动态变化的过程，不同时间段内的晶体所受应力和基体的应变很难通过理论分析得到，因此通过数值分析方法辅助计算混凝土徐变。数值模型包括微观结构的建立及加载过程中晶体应力和基体变形的计算两部分。

水泥加水拌合后，熟料迅速水化，生成大量的C-S-H凝胶以及CH和AFt等晶体。由于硅酸盐水泥水化产物除CH外的其他晶体含量较少，故本研究只考虑CH这一种晶体。熟料水化的化学式为[14]：

根据以上化学计量反应式，C3S水化生成61%的C-S-H和39%的CH，C2S水化生成82%的C-S-H和18%的CH[14]，因此，C-S-H和CH的含量分别为：

式中：fC3S、fC2S——分别为C3S、C2S的含量；

αC3S、αC2S——分别为C3S、C2S的水化程度。

假设C3S和C2S的水化程度与水泥的水化程度相同，不同龄期的水化程度如图3所示[15]。根据Power's模型[16]，水泥水化后的孔隙率φ与水灰比W/C和水化程度α相关：

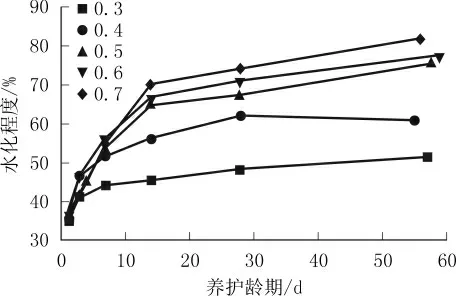
图3 水泥不同养护龄期的水化程度

因此，C-S-H和CH的相对含量分别为：

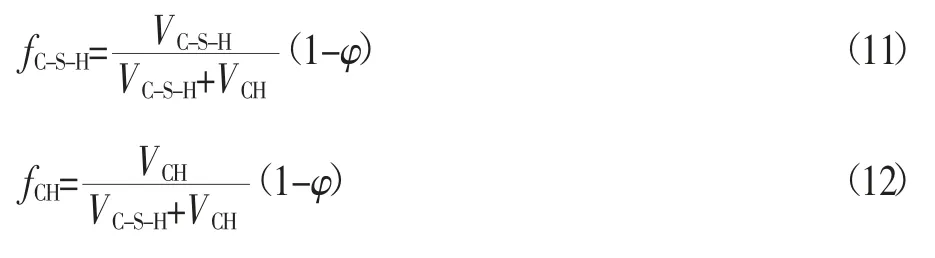
在硅酸盐水泥的水化产物中，CH晶体尺寸为7~19 μm[17]。因此，在考虑晶体受压溶解对徐变的影响时，只需考虑7~19 μm之间的孔隙中的晶体即可。C-S-H的弹性模量和泊松比分别为29.4 GPa和0.24，CH的弹性模量和泊松比分别为38 GPa和0.31[18]。本文利用有限元软件ANSYS建立模型，假设只有50%的晶体承受应力作用，且晶体分布方向与外荷载方向平行。采用蒙特卡洛法在基体二维平面内生成随机分布坐标来确定孔隙位置，C-S-H和CH采用二维平面单元建模，采用线线接触模型来模拟C-S-H和CH之间的界面，随后划分网格，使用八节点四边形的平面应变单元。将模型的横向位移和竖向位移固定，将应力施加在模型的顶部与底部。胶体和晶体微观结构的有限元模型生成示例如图4所示。利用该有限元模型计算在一定的晶体溶解长度下，作用在晶体上的应力和基体的徐变。再将该应力代入式（5），得到徐变时间。将一定的晶体溶解长度下基体的徐变和徐变时间相对应，计算过程如图5所示，从而得到徐变-时间曲线。

图4 有限元模型示例

图5 徐变-时间图的计算流程

2 混凝土徐变试验研究

水泥：42.5级低热硅酸盐水泥，水泥熟料的矿物组成见表1；粗骨料：灰岩碎石，粗骨料级配为m（80~120 mm特大石）∶m（40~80 mm大石）∶m（20~40 mm中石）∶m（5~20 mm小石）=30∶30∶20∶20，其硫化物及硫酸盐含量为0.04%，振实密度为1944 kg/m3，孔隙率为28.1%；细骨料：灰岩机制砂，细度模数2.69；拌和用水：自来水；减水剂：江苏博特JM-Ⅱ高效减水剂，固含量93.3%，减水率22.3%；引气剂：江苏博特GYQ（Ⅰ）高效引气剂；粉煤灰：曲靖Ⅰ级，主要性能见表2。

表1 低热硅酸盐水泥熟料的矿物组成 %

表2 曲靖Ⅰ级粉煤灰的主要技术性能

试验混凝土设计强度等级为C40，配合比见表3。每个徐变加载龄期需要成型的混凝土试件包括：（1）150 mm×150 mm×150 mm混凝土立方体试件3个，用于测试混凝土的抗压强度；（2）φ150 mm×450 mm的圆柱体试件不少于2个，用于测试总应变；（3）同一批徐变试验还需成型φ150 mm×450 mm的圆柱体试件2个，作为补偿试件，用于测试混凝土自生体积变形和温度变形。测试变形的试件成型时在试件中心预埋电阻式应变计，拆模后对试件用铝箔密封，保证拆模后的试件与外界没有水分交换。试件养护到加载龄期后，将试件移至徐变室[温度为（20±2）℃]进行试验。混凝土试件的加载龄期分别为28、90、180 d，加荷应力为该龄期徐变抗压强度（由立方体抗压强度折算）的30%。在进行徐变试验之前，测试每个龄期混凝土试件相应的抗压强度和弹性模量，从而确定徐变试验所需的应力及用于后续的徐变结果处理。另外，补偿试件与徐变试件采取同样的处理方法，在试验过程将其置于徐变试件旁。

表3 混凝土的配合比

徐变试验的相关参数与混凝土的力学性能如表4所示。

表4 徐变试验相关参数与混凝土的力学性能

本文将加荷试件的总应变减去收缩应变和弹性应变得到混凝土的基本徐变，其计算公式如下：

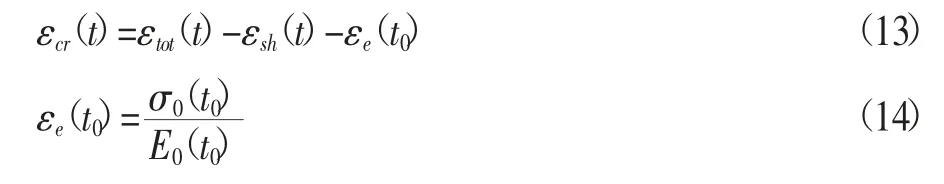
式中：εcr（t）——t时刻产生的徐变；

εtot（t）——加荷试件在t时刻测得的总应变；

εsh（t）——补偿试件在t时刻测得的应变值（自生体积变形和温度变形）；

εe（t0）——t0时刻产生的瞬时弹性应变；

σ0（t0）——t0时刻施加的恒定应力，MPa；

E0（t0）——t0时刻的弹性模量，MPa。

由于不同加载龄期下作用在混凝土上的应力不同，为消除应力对混凝土徐变的影响，可以通过徐变度来进行比较，徐变度为单位应力下的压缩徐变[1]，即：

式中：Ccr——试件在某时刻的徐变度，10-6/MPa。

3 结果与分析

采用水化产物迁移理论，对加载龄期为28、90、180 d的混凝土进行徐变试验，由式（6）~式（12）计算得到的数值模型所需的相关参数如表5所示。不同加载龄期混凝土的徐变度试验结果与数值分析结果如图6所示。

表5 模型分析所需的相关参数

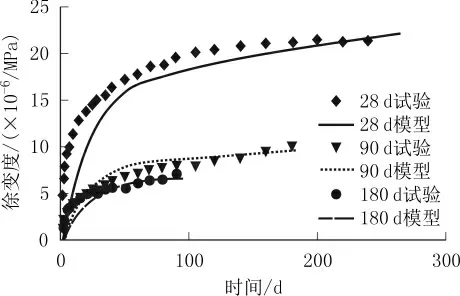
图6 不同加载龄期混凝土徐变试验与数值分析结果对比

由图6可见，加载龄期对徐变特性的影响较大，徐变度随着加载龄期的延长而减小；不同加载龄期的徐变度试验值与数值分析曲线基本一致，基于水化产物迁移理论能够较好地分析不同加载龄期的混凝土徐变特征。造成数值分析与试验值之间差异的原因可能是，模型分析中水泥净浆微观结构模型简化了C-S-H和CH的结构及其相互作用，另外该模型忽略了除C-S-H和CH之外的其他水化产物的影响。

采用水化产物迁移理论模型，可分析水化产物晶体上的应力与徐变的内在关系。将作用在晶体上的应力与作用在基体上的应力相除，得到单位应力下作用在晶体上的应力随着时间的变化，称之为作用在晶体上的应力比，如图7所示。单位应力下的溶解量如表6所示。

图7 作用在晶体上的应力演变

表6 不同加载龄期的晶体溶解量

由图7可见，随着加载龄期的延长以及晶体的不断溶解，作用在晶体上的应力逐渐减小，而徐变随时间延长逐渐增大，故作用在晶体上的应力与徐变成负相关，说明水化产物晶体应力是徐变的决定性因素。

由表6可见，随着加载龄期的延长，单位应力下晶体的溶解量逐渐减小，且基体的徐变度也逐渐减小，则徐变度与单位应力下的晶体溶解量成正比，这也说明基体徐变与晶体受压溶解之间的相关性。由表6可以得出，随着水泥加载龄期的延长，水化产物不断增加且孔隙不断减小，混凝土内部逐渐密实，等效弹性模量增大，因此徐变度随之减小。