M-矩阵线性方程组的一类非定常迭代法*

关晋瑞，温瑞萍

（太原师范学院数学系，山西晋中 030619）

0 引 言

在科学计算和工程应用中，许多问题最终都归结为线性方程组的求解，因此研究线性方程组解的理论以及求解方法具有重要的理论意义和应用价值［1-4］.如何快速有效地求得线性方程组的解是计算数学的一个基本问题，也是目前仍在继续研究的重要课题之一［5-16］.

本文考虑M-矩阵线性方程组的求解

式中A∈ Rn×n是非奇异的M-矩阵，b∈ Rn是给定的向量.这种类型的线性方程组在微分方程数值解、线性互补问题、Markov链以及物理学、生物学和经济学中都有着广泛的应用［2，4，17］.例如，对于 Poisson方程第一边值问题，利用差分法离散化之后即得到一个系数矩阵为M-矩阵的线性方程组.在线性互补问题中，很多情况下的系数矩阵都是M-矩阵.在经济学中，投入产出分析对应的矩阵也是M-矩阵［17］.

对于一般的线性方程组已有很多经典的解法，如Gauss消去法、平方根法、Jacobi迭代法、Gauss-Seidel迭代法、SOR、共轭梯度法、Krylov子空间方法［1-4］和 HSS 迭代法［18］等.而对于一些具有特殊性质和结构的方程组，也有很多学者进行了深入研究.本文利用M-矩阵的特点，针对M-矩阵线性方程组提出了一类迭代法.理论分析和数值实验表明，新方法是可行的，而且在一定情况下也是较为有效的.

1 预备知识

首先简要介绍本文的符号记法及将要用到的一些预备知识.

Rm×n表示实数域上全体m×n的矩阵，Rn表示实数域上全体n维列向量，ρ(A)表示矩阵A的谱半径.n阶单位矩阵记为In，在没有混淆的情况下写为I.用||·||来表示一个给定的矩阵范数.

设A=(aij)∈ Rn×n，若A的每个元素都是非负的，则称A为非负矩阵，记为A≥ 0.设A=(aij)∈ Rn×n，若对于任意的i≠j都有aij≤0成立，则称A为Z-矩阵.一个Z-矩阵A若可以表示为A=sI-B，其中B为非负矩阵且s≥ρ(B)，则称该Z-矩阵为M-矩阵.特别地，当s＞ρ(B)时，称A为非奇异的M-矩阵，当s=ρ(B)时，称A为奇异的M-矩阵.关于M-矩阵的详细内容可参考文献［17］.

分裂迭代法是求解线性方程组（1）的最简单的一类迭代法.分裂迭代法的基本思路是，给定系数矩阵A的一个分裂

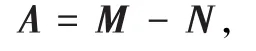
式中M是可逆的，代入式（1）得到原方程组的等价形式Mx=Nx+b，进而可以得到迭代法

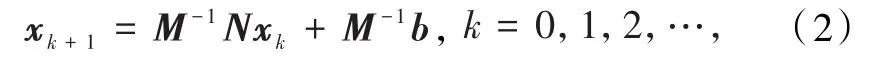
式中M-1N称为分裂迭代法（2）的迭代矩阵.

如果对于任意给定的初始向量x0∈Rn，由式（2）生成的序列{xk}都收敛于方程组（1）的解x*，则称迭代法（2）是收敛的.

引理1.1［19］分裂迭代法（2）收敛当且仅当迭代矩阵M-1N的谱半径ρ(M-1N)＜1.

引理 1.2［20］设 ||·||是任意一个矩阵范数，则对任意的A∈Rn×n有

2 一类非定常迭代法

本节提出一类非定常迭代法，以求解M-矩阵线性方程组，并给出该方法的收敛性分析.

设A=(aij)∈ Rn×n为非奇异的 M-矩阵，则A存在自然的分裂

式中s＞0，而B≥0是非负矩阵.事实上，不难验证只要选取，令B=sI-A即可.于是基于上述分裂便可以得到如下的一类迭代法

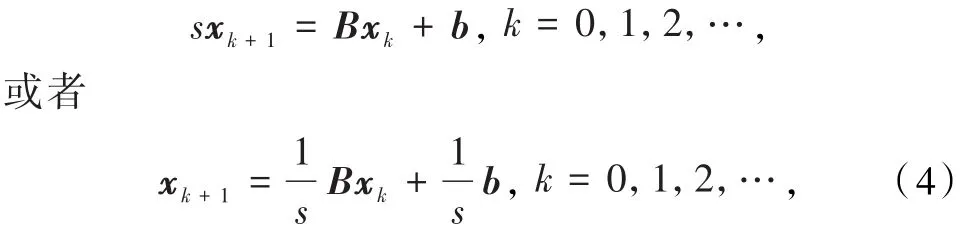
式中x0∈Rn是任意给定的初始向量.

由于A是非奇异的M-矩阵，可知s＞ρ(B).于是利用引理1.1，可得到如下的收敛性.

定理2.1设线性方程组（1）的系数矩阵是非奇异的M-矩阵，则对于任意给定的初始向量，迭代法（4）都是收敛的.

在迭代法（4）中存在一个参数s.下面讨论参数s对迭代的影响，并给出最优参数的值.

定理2.2迭代法（4）中的最优参数为

证明设A=s1I-B1=s2I-B2为矩阵A的2个分裂，其中s1，都是正数，且s1＞s2，而B1，B2是非负矩阵.相应的迭代矩阵谱半径分别为

由B1=(s1-s2)I+B2，且ρ(B1)=s1-s2+ρ(B2)，可得

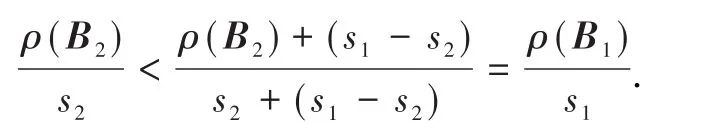
因此，参数s越小，收敛越快.从而当时，迭代法（4）收敛最快.证毕.

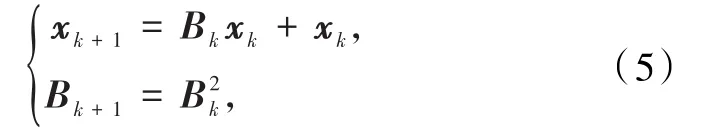
定理2.3设线性方程组（1）的系数矩阵为非奇异的M-矩阵，则迭代法（5）是收敛的，且具有二次收敛率.

证明由迭代法（4）可得方程组的精确解为

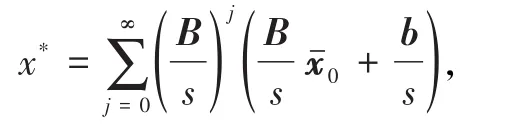
式中0为（4）的初始向量.直接验证可知非定常迭代法（5）得到的序列{xk} 满足

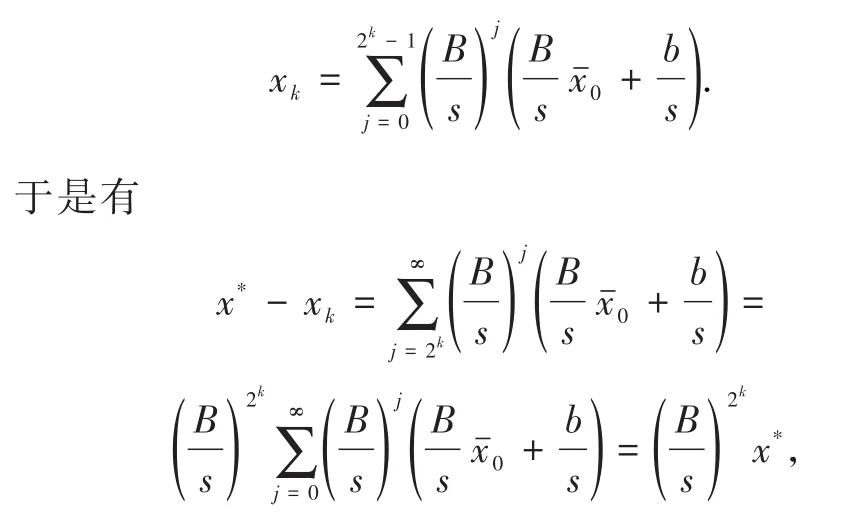
两边取范数，并利用引理1.2，可得

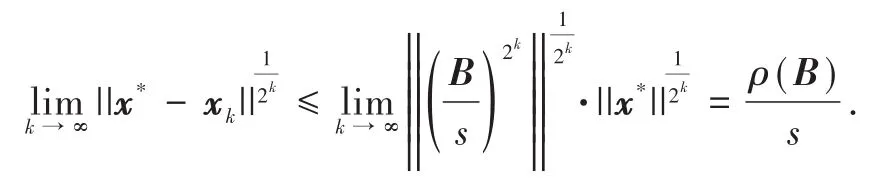
因此，序列{xk}是收敛的且具有二次收敛率.证毕.

尽管非定常迭代（5）相对于（4）运算量较大，但是上面的定理表明迭代收敛很快.因此是可行的.

3 数值实验

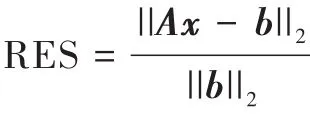
例 3.1［19］考虑M-矩阵线性方程组（1），其中

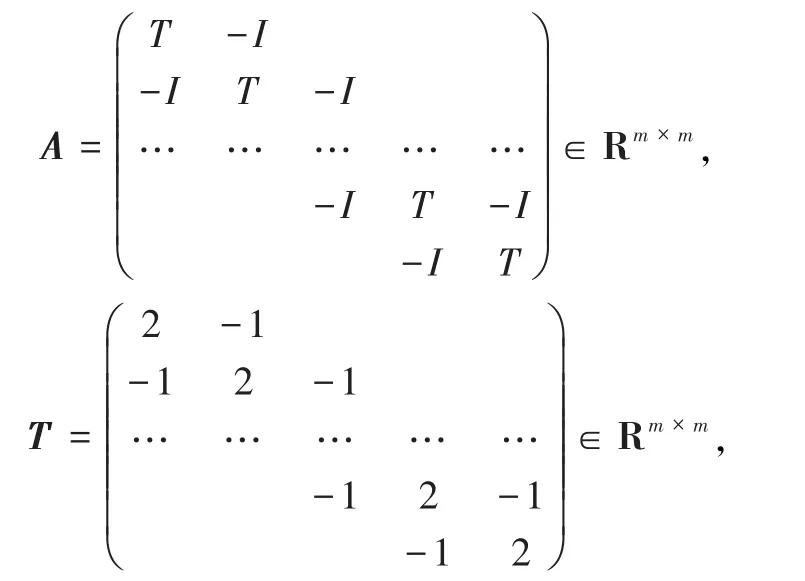
而n=m2，b=(1，1，…，1)T∈ Rn.当m取不同值，2个迭代法得出的结果如表1所示.与迭代法（4）相比，迭代法（5）不仅迭代次数和运行时间都明显要少，而且求得解的精度也高.特别地，当系数矩阵的阶数增加时，迭代法（4）的迭代次数急剧增加，但迭代法（5）的迭代次数增加不明显.

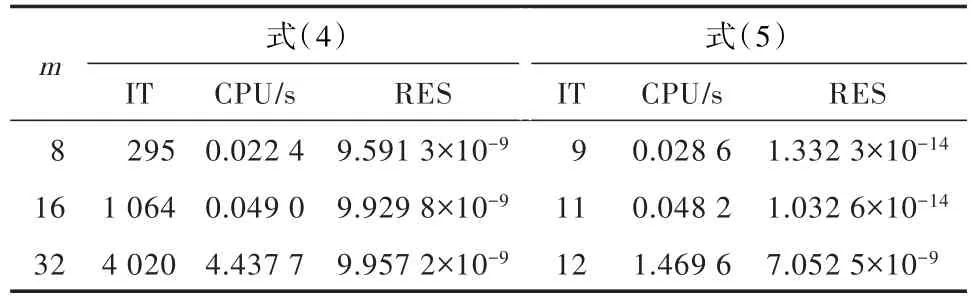
表1 m取不同值时不同迭代公式对应的结果

例3.2考虑M-矩阵线性方程组（1），其中A由下列命令生成

a=rand（n，n）；A=diag（a*ones（n，1））-a+eye（n）；而b=(1，1，…，1)T∈ Rn.对于阶数n的不同取值，表2中给出了实验结果.从表2中可见，随着系数矩阵阶数的增加，迭代法（4）的迭代次数与运行时间都急剧增加，但迭代法（5）的迭代次数和运行时间并没有明显的增加.

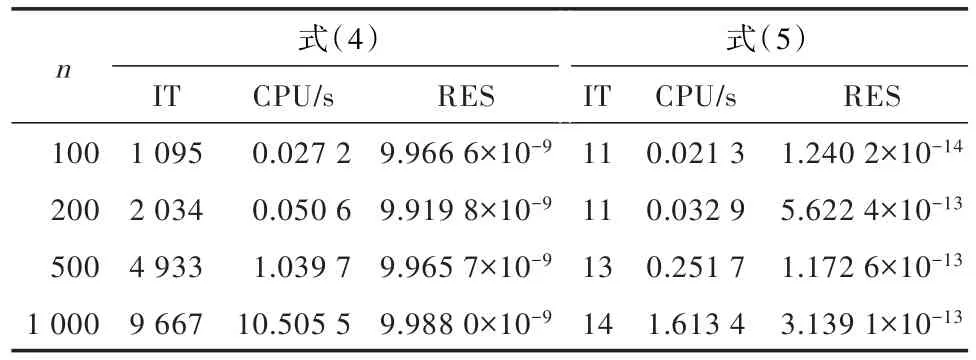
表2 n取不同值时不同迭代公式对应的结果

例3.3考虑M-矩阵线性方程组（1），其中

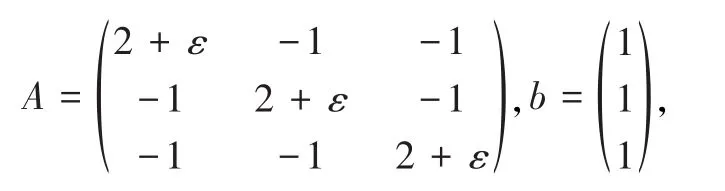
ε＞0是正数.当ε→ 0时，矩阵A接近奇异.对于参数ε的不同取值，实验结果见表3.当参数越来越小时，迭代法（4）的迭代次数急剧增加，但迭代法（5）的迭代次数并没有明显的增加.

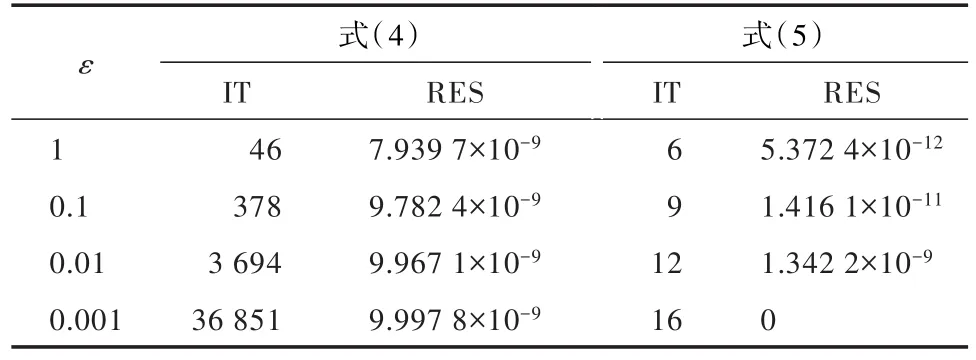
表3 参数取不同值时不同迭代公式对应的结果

由以上3个数值例子可见，迭代法（4）收敛较慢，特别当系数矩阵接近奇异时，收敛非常缓慢，而迭代法（5）始终收敛很快，且求得解的精度也比较高，因此迭代法（5）是较为有效的.

4 结束语

本文提出了一类非定常迭代法以求解M-矩阵线性方程组.理论分析表明该方法具有二次收敛率.数值实验表明，该方法是可行的，而且在一定情况下也是较为有效的.但是该方法在每步迭代中运算量较大，如何减少运算量并保持较快的收敛速度，还有待进一步的研究.另外，由于H-矩阵和M-矩阵具有很多相近的性质，本文的方法还可以推广到H-矩阵线性方程组.