旋成体凹坑数控加工方法研究

刘力源，舒启林

(沈阳理工大学 机械工程学院，沈阳 110159)

在表面功能减阻的研究中，旋成体非光滑表面减阻效果已经得到了科学实验的验证。在一定的来流速度下，旋成体表面会存在剪切应力；当有凹坑存在时，凹坑单元体内会产生一个低压区，使得凹坑下游的区域压力减小，因此非光滑表面能起到良好的减阻效果[1]。目前凹坑的加工方法主要为电化学微加工法[2]，该方法通过不断的腐蚀，在光滑表面加工通孔或有排列的不同深度的凹坑，缺点是无法加工特定排列顺序的凹坑。Jiwang Yan[3]通过金刚石铣刀加工凹坑，加工的最小直径可达282μm，但无法在曲面上加工凹坑。樊晶明等[4]用微磨料空气射流，在平板玻璃上研究冲蚀凹坑的形貌，该方法加工的凹坑精度较高但效率较低，无法快速获得指定深度的凹坑且无法应用于曲面。曾繁铿等[5]通过纳秒激光逐层铣削工件表面的方法加工凹坑，该加工方法受光斑能量的影响，会导致材料去除不均且效率低。刘峰等[6]对纳秒激光刻蚀技术进行了改进，将纳秒激光刻蚀后的工件放入离子束刻蚀设备中，能够很好地改善凹坑的表面质量，但该方法成本高且效率低。薛腾等[7]运用干膜的掩模电解加工技术在基片表面加工出不同深径比的微凹坑，且其表面形貌良好，但加工过程中稳定性难以保证，且电解产物回收和处理比较困难。赵昌龙等[8]利用电火花技术，利用工件与电极间脉冲放电产生瞬时高温使金属表面被蚀除；该加工方法对温度控制和蚀除时间要求比较严格，凹坑尺寸控制难度较大。综上所述，目前对于凹坑的加工大多在平面上且效率较低。本文提出一种曲面凹坑的数控加工及刀具轨迹优化方法，通过计算刀轴矢量、走刀步长和加工刀位一系列参数，保证曲面铣削凹坑的精度；通过刀具轨迹规划，选择出优化后的刀路，提高加工效率。

1 旋成体凹坑的排布及三维建模

旋成体是由一条母线沿旋转轴旋转而形成的实体，在装备行业较为常见，本文选取的旋成体母线图如图1所示。

图1 旋成体母线图

图1旋成体表面凹坑的排布方式为植物叶序排布，相邻叶序点之间夹角为137.508°，如图2所示。

图2中a1和b1是新生长出来的叶片，a1和a2、b1和b2的夹角是137.508°，同理a2和a3、b2和b3的夹角也是137.508°；叶片的大小按一定比例生长变化，当叶片生长到一定程度后，大小不再变化，即为成熟。将叶序排布应用于旋成体上，用凹坑的排布方式和比例变化模拟植物叶片的生长规律。旋成体圆弧部分是生长区，凹坑尺寸不断变化；圆柱部分是成熟区，凹坑尺寸不变。旋成体圆弧部分叶序点排布方式按一定比例逐渐收缩，凹坑的深度和直径也按照一定比例减小。遵循公式为[9]

图2 植物叶序排布规律图

an[t]=a0ek(n-N)，n=1，2，3，4，…，N

(1)

式中：a0是圆柱部分凹坑的面积；an为圆弧部分凹坑的面积；n为叶序点成长次序；k为生长系数，限制相邻两个凹坑面积的变化比例(按照指数比例变化)。

通过计算得出在此旋成体尺寸下符合减阻要求的圆柱部分凹坑直径为3mm，深度为0.6mm，圆弧部分的凹坑按照式(1)进行一定比例的收缩。通过三维建模，得出在此旋成体尺寸下的旋成体模型及凹坑排布方式，如图3所示。

图3 旋成体三维模型

图3中，旋成体头部为仿生植物生长区域，头部的凹坑直径和深度按照指数规律逐渐变化，轴向距离决定于尺寸变化比例；体部为仿生植物成熟区，凹坑尺寸不再变化，尺寸直径3mm，深度0.6mm。

2 旋成体凹坑的数控加工方法

由于加工的形状是凹坑，所以采用铣削加工方法，刀具选择球头立铣刀加工比较合理。选用球头铣刀直径为4mm，当凹坑深度为0.6mm时，加工出来的凹坑直径为2.9mm。

2.1 数控加工待解决的问题

在数控铣削凹坑的加工过程中，需要解决两个主要问题：(1)球头铣刀刀具轴线必须和叶序点所在平面的法向量重合，如果刀具轴线不与法向量重合，则加工出来的凹坑表面不是圆形而是椭圆形且凹坑深度无法保证，影响减阻效果；(2)由于旋成体圆弧部分曲率不断变化，如按照固定的抬刀距离加工，会使加工质量不符合要求，甚至会导致刀具移动过程中与工件发生碰撞干涉，造成加工事故。所以在数控加工前，要设计好刀具轨迹，使得加工过程中既不发生干涉又能达到较好的加工效果。

2.2 旋成体圆弧部分叶序点所在平面法向量的确定

在旋成体圆弧部分排布的凹坑，相邻凹坑间轴向距离和径向距离不断变化，且加工的表面是曲面，所以首先要计算在任意选定的一个叶序点上平面的法向量，以保证加工时刀具轴线与叶序点所在平面法向量共线。由于旋成体圆弧部分的母线取自半径为100mm的圆的一部分，根据相关数学知识可知，在圆弧部分的任一叶序点的法向量所在直线必然经过半径为100mm的圆的圆心。任取旋成体圆弧处一叶序点p，p与圆心O连线，则此叶序点所在平面的法向量np如图4所示。

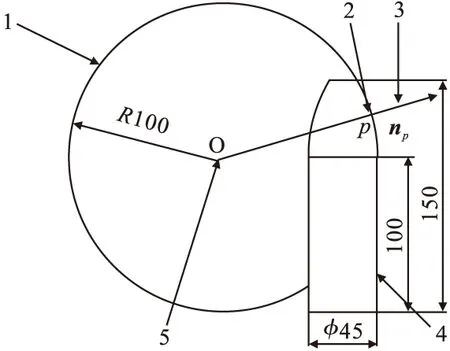
图4 任一叶序点所在平面法向量

图4中1是旋成体圆弧部分所在圆；2是旋成体圆弧部分任意一点p；3是旋成体任一点p的法向量；4是旋成体母线图；5是旋成体圆弧部分所在圆的圆心。加工点p处刀轴矢量与np共线。以此类推，即可求解出旋成体圆弧部分任意叶序点所在平面的法向量。圆柱部分的旋成体叶序点所在平面的法向量求解比较简单，因为相邻凹坑所在曲面曲率变化是固定的，任取一个旋成体叶序点，其所在平面法向量与此叶序点到其所在圆圆心的连线共线。在计算好叶序点所在平面法向量后，可确定球头铣刀的刀具轴线，保证刀具轴线和法向量所在直线重合，即可保证球头铣刀在加工时，刀具轴线始终保持和圆弧面或圆柱面垂直，从而保证加工出来的外形是凹坑外形。

2.3 旋成体圆弧部分叶序点加工刀位的确定

在球头铣刀进行铣削加工时，刀位一般指球头铣刀的球头中心，在圆弧面上加工任一叶序点p处的刀位计算方法为[10]

rc=ra+Rn1

(2)

式中：rc为铣刀球头中心点的点矢量；ra为叶序点p的点矢量；R为刀具半径；n1为p所在平面的单位法向量(即刀轴矢量)。图5为球头铣刀铣削曲面任一点p的刀位图。

图5 任意一叶序点刀位

2.4 凹坑加工步长的确定

步长是刀位轨迹规划的一项重要参数，由于加工的表面为曲面，所以刀位轨迹也是曲线；在数控加工过程中，通过一系列刀位点逼近刀位轨迹来达到加工曲面的目的。步长的计算方法有等弦长步长法、等参数步长法和等弦高步长法。

等弦长步长计算方法计算的前提是保证相邻刀位点间的弦长是一个固定值，在确定好第一个刀位点后，以确定好的半径(即确定好的固定弦长)做球，球面与曲面的交点就是下一个刀位点。等参数步长计算方法是把刀轨曲线放在坐标系中，通过确定好恒定的增量d，使d对应于刀轨曲线上的刀位点；这种计算方法比较简单，但是增量d的选取比较困难，如果选择的增量d较大，则增量d不易反映出刀位轨迹曲率的变化规律，使得误差变大；如果选择较小的增量d，虽然能保证反映出刀位轨迹曲率的变化，但会产生过多的冗余刀位点，极大地影响加工的效率。等弦高步长的计算方法是保证相邻刀位点之间的弦高差(用△h表示)，通过计算曲线上相邻数据点曲率和△h之间的关系，求得弦高的大小，再通过固定的弦高确定步长，这种计算方法比较简单且可保证加工精度的要求。

综上所述，本文选择等弦高步长法计算走刀步长，如图6所示。

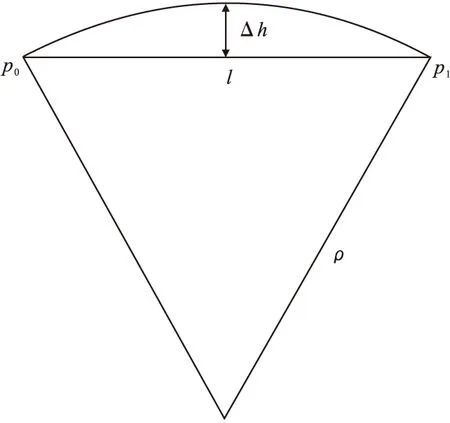
图6 等弦高步长

把两个相邻刀位点的刀具轨迹用圆弧近似，此时将刀位点p0处的曲率ρ作为圆弧的半径，弦高差用△h表示，步长用l表示，下一个刀位点用p1表示，则有

(3)

由于旋成体圆弧部分和圆柱部分表面曲率变化不大，且加工旋成体表面时，刀位轨迹接近于圆弧，所以△h非常小，计算过程中△h2可忽略不计，故有

(4)

在已知加工过程中存在的最大弦高基础上，可计算出最小走刀步长为

(5)

2.5 加工刀具摆动的计算

旋成体表面相邻叶序点排布按照137.508°角度进行布置；进行刀具摆动角度计算时，只需要计算刀具轴线的摆动角度即可反映出刀具的摆动角度。前文中提到，刀具轴线要始终和旋成体表面叶序点所在平面的法向量共线，所以刀具的摆动角度要根据实际加工过程中选取的叶序点加工顺序进行确定。现选取以下两种叶序点加工顺序进行刀具摆动角度的计算。

(1)图7为按照相邻叶序点排布角度137.508°计算。

图7 第一种加工顺序的刀具摆动

图7加工顺序的刀具摆动是加工第一个叶序点t1后，刀具摆动137.508°加工第二个叶序点t2，然后再旋转137.508°加工第三个叶序点t3。从而完成相邻叶序点的加工。

(2)图8为按照旋成体表面叶序点距离最近计算。

图8 第二种加工顺序的刀具摆动

图8加工顺序的刀具摆动是加工第一个叶序点t1后，加工t4；t4是相对于t3的下一个叶序点，即与t3的夹角是137.508°，而t4相对于t1的角度是52.524°，这样保证了刀具摆动的角度不至于过大。

3 加工中曲面刀位轨迹的生成方法

在确定好刀具轴线、走刀步长和刀具摆动后，即可进行叶序排布凹坑的数控加工刀具轨迹规划。球头铣刀的刀位即铣刀的球头中心，所以加工旋成体表面时的刀位轨迹就是球头中心点的运动轨迹。本文利用Unigraphics NX加工模块进行叶序点的数控加工仿真，并规划几种类型的刀具轨迹，对每种刀具轨迹的优缺点进行分析。

3.1 加工仿真参数设置

选用的加工刀具是直径为4mm的球头铣刀。由于旋成体表面凹坑的直径和深度都较小，所以选择孔铣的加工命令，通过调整进刀深度来控制表面凹坑的深度和直径，以达到旋成体圆弧部分叶序点凹坑渐缩的要求。在加工凹坑时，应设定一定的刀具停留时间，才能获得较好的加工质量，所以一个凹坑的停留时间设置为5s。球头铣刀径向进给量的设置也至关重要，表面凹坑的尺寸形状较小，如果进给量过大，则无法加工出指定深度和直径的凹坑，达不到减阻效果，使得加工没有意义；如果进给量过小，会使凹坑深度和直径较小，影响减阻效果，所以选取进给量300mm/min，转速设置为3000r/min。

3.2 走刀轨迹的设计与分析

第一种走刀轨迹按照旋成体叶序排布夹角137.508°加工时，加工仿真刀具轨迹如图9所示。

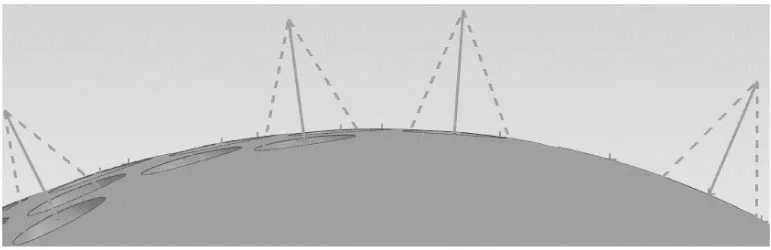
图9 第一种走刀轨迹

图9加工轨迹要求刀具在加工完第一个凹坑后，刀具轴线旋转137.508°进行下一个位置凹坑的加工。从图9中可以看出，按照设置生成刀具轨迹后，刀具轨迹明显与工件发生了干涉，需要设置一定的抬刀高度，才能保证刀具与工件不发生干涉；然而由于旋成体上凹坑数量较多，每两个凹坑间就要设置一个抬刀高度，抬刀高度不能过低，否则刀具与工件就会干涉。此种加工方法大大增加了走刀路径，使得加工效率降低。

第二种走刀轨迹如图10所示。

图10 第二种走刀轨迹

图10走刀轨迹根据凹坑叶序排布后形成的螺旋线进行刀具轨迹设计，此轨迹相对于第一种轨迹而言，刀具与工件不会发生干涉，且刀具摆动角度较小，优于第一种走刀轨迹；但这种走刀轨迹加工完一列凹坑后，刀具又要返回到旋成体顶部，进行第二排凹坑的加工，明显增大了走刀步长，加工效率低。

第三种走刀轨迹如图11所示。

图11 第三种走刀轨迹

图11走刀轨迹是根据走刀的最短刀轨设置的，这种加工方式是加工好一个叶序点后，计算好最短的走刀刀轨，然后去加工下一个凹坑；此加工方式不会造成刀具和工件的干涉，刀具摆动角度不大，且不需要如第二种走刀轨迹那样，回到旋成体顶部，不会造成走刀步长过长，因此提高了加工效率。

综合以上几种刀具的走刀轨迹，选取较为优化的第三种走刀轨迹作为凹坑加工的走刀轨迹。仿真加工的凹坑形貌如图12所示。

图12 仿真加工形貌

对图12所得表面形貌进行测量，如图13～14所示。圆柱部分任一凹坑直径为2.9803mm，深度为0.5945mm，符合尺寸要求。

图13 圆柱部分凹坑深度

图14 圆柱部分凹坑直径

测量圆弧部分任一凹坑尺寸，如图15～16所示。凹坑直径为2.597mm，深度为0.5677mm，符合圆弧部分减缩的形貌要求。

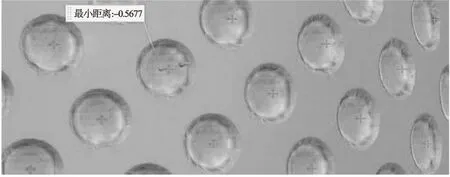
图15 圆弧部分凹坑深度

图16 圆弧部分凹坑直径

4 结论

通过计算在曲面上加工叶序排布的凹坑的刀位、刀具摆动角度、走刀路径等，使球头铣刀刀轴始终和凹坑所在平面的法向量共线，保证了圆形凹坑的加工质量；通过几种刀具轨迹的分析，选择了走刀路径最短的刀具轨迹，使得加工效率提高；通过调整进刀深度，保证了旋成体圆弧部分叶序凹坑尺寸的渐缩，为以后加工渐缩形凹坑排布提供了依据。