时滞对耦合神经元网络振动共振的影响

2021-12-30袁春华麻建新李翔宇

沈阳理工大学学报 2021年6期

袁春华，麻建新，李翔宇

(沈阳理工大学自动化与电气工程学院，沈阳110159)

将随机共振[1]中的噪声信号用高频周期信号代替，会产生一系列与随机共振相似的现象[2]。用高频信号取代噪声，增强对低频信号的放大作用，这种现象被称为振动共振。在两个频率信号的作用下，通过选择合适的高频信号可以扩大低频信号，增强低频信号的传导，使低频信号的传递更有效[3]。两个频率段的信号广泛应用于通讯技术中，在其它包括激光物理学、天体物理学、声学、神经系统科学[4-5]等领域的应用也很常见。

每个神经元都与周围神经元有上千个突触连接，构成神经网络，完成信息的传递。了解神经元突触之间的连接方式和表现形式对于研究神经网络中的信息处理特性至关重要。突触连接方式有电突触连接和化学突触连接两种形式[6]，化学突触可以分为快突触和慢突触[7]。Ullner E等[3]发现高频驱动的最优幅值增强了可激发系统对低频信号的响应，并印证了FitzHugh-Nagumo(FHN)神经元模型中可发生振动共振现象。Deng B等[8]研究了耦合神经元在高频驱动下对亚阈值低频信号的响应，并发现化学突触耦合比电突触耦合连接更有效。Agaoglu S N等[5]研究了电突触连接和单一化学突触连接的神经元集群中的振动共振现象。Li S等[9]研究了电耦合神经元网络的同步问题。上述研究通常只探究电突触或是单一类型的化学突触耦合的振动共振效应，但是电突触在哺乳类动物大脑的主要细胞内很少见，而不同类型的化学突触耦合在人的大脑内普遍存在，并扮演着不同的重要角色[10]。

网络模态是在网络里反复出现的比预期随机出现频率高很多的一些图案模式[11]。生物学、生态学以及其他一些领域里研究的绝大多数网络都显示出小组网络模态。在信息处理的网络中，模态作为基本的计算结构体有其特定的功能。模态可以定义普遍的网络种类，为揭开大多数网络最基本的构建模块的奥秘提供基础。检测和理解网络模态有助于更深入地探究神经元网络的动力学行为和定义网络的类别。研究表明，三个神经元的耦合一共有十三种不同的模态[12]。

本文研究化学突触耦合连接，分析不同类型的化学突触耦合(快或慢)对系统振动共振的影响。基于神经元传递信息存在时滞[13-14]，分析时滞对十三种模态的耦合神经元振动共振的影响，研究时滞对不同规模的耦合神经元网络振动共振的作用。

1 模型和方法

两种不同频率的信号共同驱动FHN模型，可表示为[15]

(1)

式中：x代表神经元的细胞膜电压；y代表神经元的慢变量，与细胞膜的慢变过程相关；ε为时标比率，取ε=0.01；Acos(ωt)和Bcos(Ωt)分别代表外部信号中的低频和高频成分，选择A=0.01时，单独的低频信号刺激并不能引发神经元放电；取Ω=5和ω=0.1；参数a决定了系统的动力学特性。

a>1.0时FHN模型是可兴奋型神经元，a<1.0时模型表现为振荡的行为，a=1.0是FHN模型的分岔点[8]，在分岔点附近，神经元会出现介于放电和振荡之间的状态。当参数a稍大于分岔点时，在不稳定的平衡点附近会出现低于放电行为的小幅振荡状态，称为canard振荡现象[16]。

为估计在输出信号中输入频率的幅值，由输入频率ω计算傅里叶系数Q，见公式(2)。本文重点研究频率ω中编码信息的传播，用Q参数代替能量谱。

(2)

式中n是积分时间所覆盖的周期2π/ω的数目。Q的最大值为Qmax，表示输入信号和输出放电之间最佳的相同步。Qmax对应的高频信号幅值称为最优高频扰动幅值，即BVR。

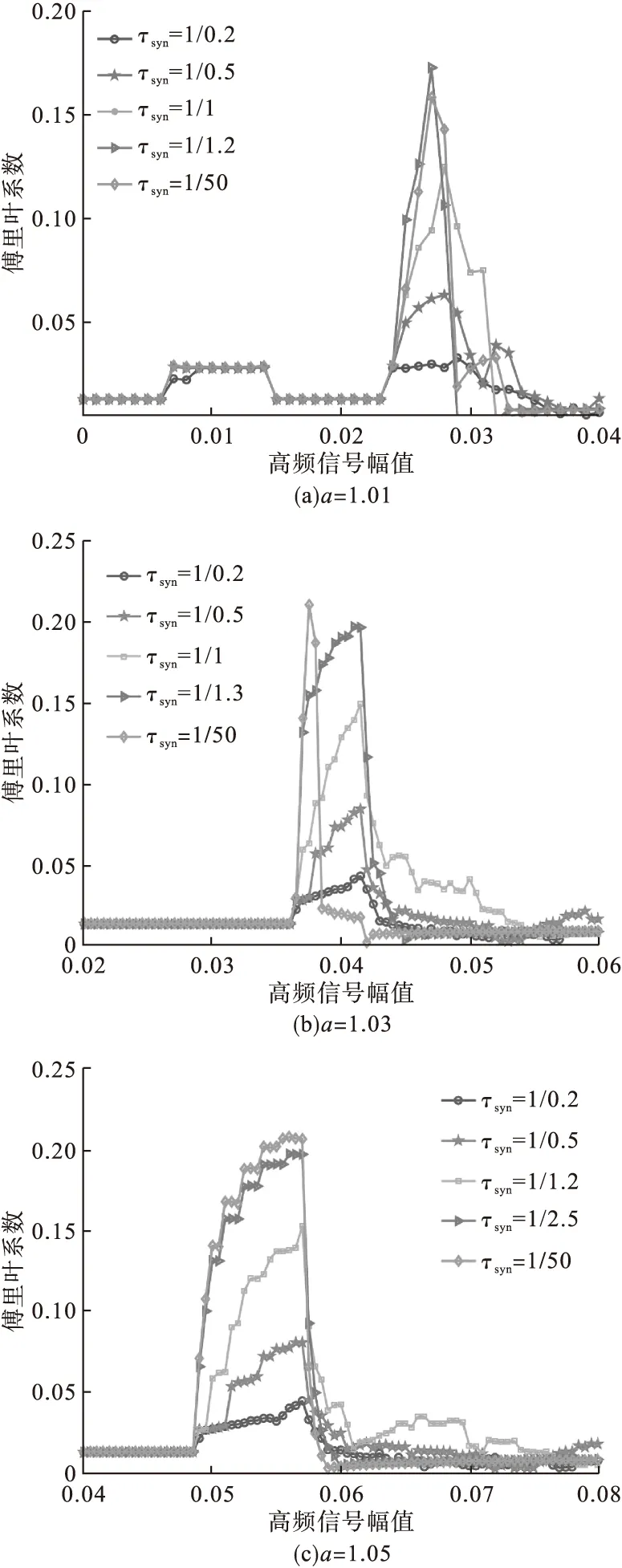
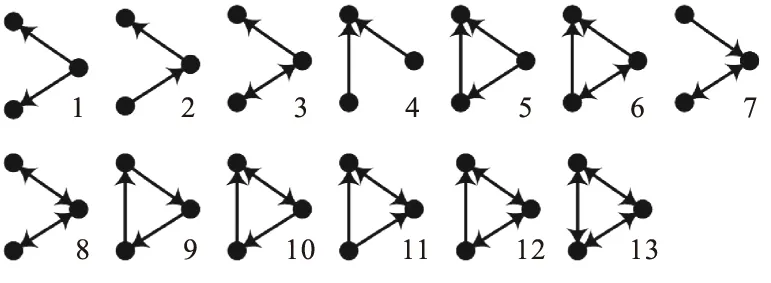
计算Q时，把阈值xS定为0。如果x

三个双向耦合的FHN神经元受到一个共同的高频驱动力，可描述为

(3)

(4)

式中：sj为突触变量；gsyn是突触耦合强度，取gsyn=0.1；xsyn是突触反电势，决定了突触的类型。对于兴奋型突触，取xsyn=0。

突触变量sj的动力学由xj控制。sj定义为

(5)

式中：τsyn为突触衰减时间常数；α(xj)为突触恢复函数，采用Heaviside函数。式中参数取值为α0=2、v0=0.05。

2 化学突触类型对耦合神经元振动共振的影响

为研究高频刺激下耦合神经元之间的信息传递，在局部刺激下研究耦合神经元的振动共振现象，即只有一个神经元受到外部低频信号刺激。用耦合神经元放电序列x2计算Q值，不采用三个神经元放电序列的平均值(由于耦合的对称性，用x3计算取得的结果相同)。输入周期信号的参数取值分别为A1=0.01、A2=0、A3=0、ω=0.1、Ω=5，以保证在没有高频扰动的情况下神经元不会放电。

为研究化学突触中重要参数τsyn对耦合神经元放电的影响，分别取a=1.01、a=1.03和a=1.05，得到耦合神经元放电响应的傅里叶系数Q随高频信号幅值B的变化，如图1所示。

由图1可见，当τsyn值较大时，耦合神经元没有共振放电，当τsyn减小到某一值时，耦合神经元开始放电。

图1 耦合神经元放电响应的傅里叶系数Q与高频信号幅值B的关系

当a=1.01时，最优高频扰动幅值BVR逐渐减小最后趋于不变，而Q的最大值Qmax逐渐增大最后趋于不变。说明随着τsyn的减小，系统达到共振需加入的高频信号幅值逐渐减小，即传递信息所需的能量逐渐减小，但共振强度逐渐增加，信息传递效率逐渐增强。当a=1.03时，最优高频扰动幅值BVR先基本不变最后减小，Qmax逐渐增大最后趋于不变。说明随着τsyn的减小，系统达到共振需加入的高频信号幅值先基本持平后逐渐减小，共振强度逐渐增加最后趋于不变。系统传递信息的效率在τsyn较大时基本一致，在τsyn较小时逐渐增强。而当a=1.05时，最优高频扰动幅值BVR基本保持恒定不变，Qmax逐渐增大最后趋于不变，即突触衰减时间常数τsyn对此时耦合神经元系统的信息传递效率几乎没有影响，只是随着τsyn的减小，共振强度逐渐增大，耦合神经元放电的同步性变好。

和图1相对应的突触变量s随时间t的变化情况如图2所示。