应用动态数学软件探究铅球投掷问题

一、问题的提出

物理是一门基于实验探究物体运动规律的学科，也是一门经常应用数学知识的学科。多数高中生数学基础不扎实且跨学科知识融合能力较弱，学习物理学科内容时，往往不能有效应用数学知识解决物理问题，更谈不上感受科学之美。例如，被投掷的铅球在空中的运动属于斜抛运动，也是高中生常见的一种抛体运动。探究不同条件下投掷铅球的最优方案，涉及铅球被投掷时的初速度大小、抛出点高度和抛出角等因素，如果应用高等数学知识求解极值来探究，显然超出高中生的数学能力范畴，也不利于学生理解。面对物理和数学两门学科，学生通常感到公式多、抽象化难理解。如何走出困境？高中生对动态的、图象化的情境更感兴趣。将问题解决过程可视化无疑是一种有益的尝试。

当前，信息技术为教育高度赋能，功能各异的软件凭借各自特色技术融入教学之中。例如，GeoGebra是一款跨平台动态数学软件，它不仅提供了针对几何、代数、表格、图形、统计和微积分等对象的强大分析功能，而且允许用户借助电脑端、网页在线使用，还支持平板电脑等移动终端应用。用户应用GeoGebra可创建各种复杂函数，并通过2D和3D的方式实时动态化展示函数的变化情况，通过交互操作实现互动功能。

抛体运动是高中物理课程中学生遇到的第一种曲线运动。学生在系统学习了匀速直线运动和匀变速直线运动后，首次综合运用所学知识解决复杂运动。各种版本的高中物理教材均详细探究了平抛运动这种特殊的抛体运动，但学生在日常生活中更多遇到的是初速度与水平方向有一定夹角的斜抛运动，如投掷出的铅球在空中的运动。如何根据不同个体特征精准设定最优投掷参数，对于学习了平抛运动知识后跃跃欲试的高中生而言，这是极具诱惑力的尝试，也是一个颇具挑战难度的研究性学习课题。

二、应用GeoGebra研究铅球的投掷问题

（一）铅球运动过程的理论分析

在忽略空气阻力的情况下，被投掷的铅球在空中的运动可以分解为水平方向上的匀速直线运动和竖直方向上的匀变速直线运动。

根据运动学公式，铅球在水平方向的位移和竖直方向上的位移分别如下（式1和式2）。

= cos （1）

=+ sin - ² （2）

将式1和式2联立消去时间，得到如下表达式（式3）。

=+ tan - ² （3）

当铅球落地时，其竖直方向上位移=0，即有

+ tan - ² = 0 （4）

通过求根公式

= （5）

可得铅球的投掷距离为

= （6）

分析式6后发现，决定铅球投掷距离的因素包括抛出时初速度、抛出角度和抛出点高度。

如何求解铅球投掷距离最远的参数条件？如果继续从数学理论角度推导是不可信的，因为要用到高等数学知识会超出中学生的理解范畴，还不够直观、生动。

（二）铅球投掷参数的可视化分析

笔者打开GeoGebra的图形计算器后，新建两个滑动条，分别用来控制铅球抛出时的初速度和高度，综合考虑高中生所处年龄段特点和参考运动员投掷铅球的数据^[1]，输入命令定义变量：

=slider（0，13，1）

=slider（1.5，2.5，0.1）

上面命令中用到了GeoGebra内置的slider命令，三个参数分别是最小值、最大值和步长。

接着定义函数（式7）：

（）= （7）

式（7）中取重力加速度=9.8 m/s²，其中为抛出角，在右上角符号为度（在函数定义过程中通过快捷键“Alt+O”实现）。这里，GeoGebra用度为单位运算，否则软件默认采用弧度制单位。为使GeoGebra绘制的函数图象与实际相符，需要将的取值范围规定为小于等于90°。命令如下：

L1（）=if（0≤≤90，L（））

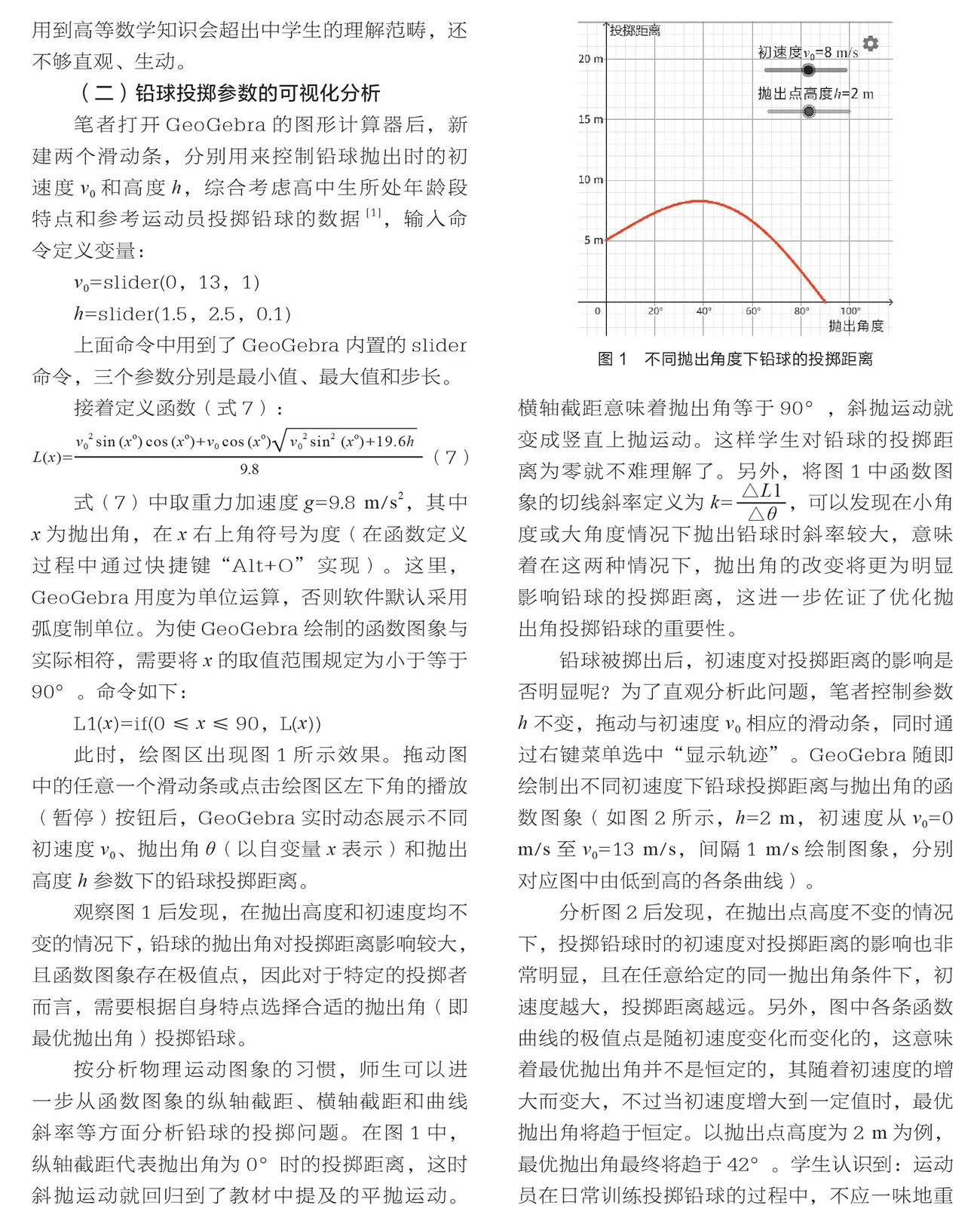
此时，绘图区出现图1所示效果。拖动图中的任意一个滑动条或点击绘图区左下角的播放（暂停）按钮后，GeoGebra实时动态展示不同初速度、抛出角（以自变量表示）和抛出高度参数下的铅球投掷距离。

观察图1后发现，在抛出高度和初速度均不变的情况下，铅球的抛出角对投掷距离影响较大，且函数图象存在极值点，因此对于特定的投掷者而言，需要根据自身特点选择合适的抛出角（即最优抛出角）投掷铅球。

按分析物理运动图象的习惯，师生可以进一步从函数图象的纵轴截距、横轴截距和曲线斜率等方面分析铅球的投掷问题。在图1中，纵轴截距代表抛出角为0°时的投掷距离，这时斜抛运动就回归到了教材中提及的平抛运动。横轴截距意味着抛出角等于90°，斜抛运动就变成竖直上抛运动。这样学生对铅球的投掷距离为零就不难理解了。另外，将图1中函数图象的切线斜率定义为= ，可以发现在小角度或大角度情况下抛出铅球时斜率较大，意味着在这两种情况下，抛出角的改变将更为明显影响铅球的投掷距离，这进一步佐证了优化抛出角投掷铅球的重要性。

铅球被掷出后，初速度对投掷距离的影响是否明显呢？为了直观分析此问题，笔者控制参数不变，拖动与初速度相应的滑动条，同时通过右键菜单选中“显示轨迹”。GeoGebra随即绘制出不同初速度下铅球投掷距离与抛出角的函数图象（如图2所示，=2 m，初速度从=0 m/s至=13 m/s，间隔1 m/s绘制图象，分别对应图中由低到高的各条曲线）。

分析图2后发现，在抛出点高度不变的情况下，投掷铅球时的初速度对投掷距离的影响也非常明显，且在任意给定的同一抛出角条件下，初速度越大，投掷距离越远。另外，图中各条函数曲线的极值点是随初速度变化而变化的，这意味着最优抛出角并不是恒定的，其随着初速度的增大而变大，不过当初速度增大到一定值时，最优抛出角将趋于恒定。以抛出点高度为2 m为例，最优抛出角最终将趋于42°。学生认识到：运动员在日常训练投掷铅球的过程中，不应一味地重视对铅球抛出角度的控制，还应该通过体能训练和肢体动作协调等方法给予铅球足够的初速度。

对图2进一步分析后发现，图中各条函数曲线与纵轴的交点是等间距的。已知函数图象与纵轴相交时代表铅球的斜抛运动回归到平抛运动，根据平抛运动知识，可计算投掷距离（式8）。

= （8）

显然，在铅球抛出高度相同、初速度等间隔变化的情况下，函数图象与纵轴交点必然等间距分布。通过讨论，学生不仅进一步熟悉平抛运动知识，而且切身感受到学以致用的乐趣。另外，对于其他抛出角（0°<<90°）条件，函数图象之间的间距均是先增大后减小，且函数切线的斜率除极值点外均整体变大，这也进一步论证了铅球抛出初速度对投掷距离有极大影响。

抛出角度和初速度两个因素对铅球的投掷距离影响显著。为了进一步提升投掷成绩，是否有必要选拔高个子且手臂长的运动员投掷铅球呢？拖动与抛出点高度相应的滑动条，GeoGebra自动绘制出如图3所示的不同抛出高度下的投掷距离函数图象（初速度设定为=13 m/s，=1.5 m至=2.5 m，间隔0.2 m绘制图象，分别对应图中由低到高的各条曲线）。

分析图3后发现，随着抛出点高度的增加，各个抛出角度下铅球的投掷距离均有所增加，但差异并不明显。此外，图3中各条函数曲线的极值点会随着抛出点高度的增加向左侧偏移，这代表最优抛出角会随抛出点高度的增加而变小。

按物理中常用的“整体法”，图3中各条函数曲线可整合命名为“函数曲线带”。似乎这条“函数曲线带”的宽度随着抛出角的增大而变窄。为了验证此结论，在GeoGebra中命名新函数△ （）并计算图3中这条“函数曲线带”的宽度（因公式较长，在此略），并通过GeoGebra绘制出函数图象，效果如图4所示。

学生分析图4后确认：随着抛出角的增大，“函数曲线带”的宽度确实在变窄。“函数曲线带”的宽窄代表在初速度和抛出角均相同的情况下，在两种极端抛出高度下分别投掷铅球的投掷距离之差，由于图4中函数的最大值在2 m左右，实际投掷铅球时具有一定抛出角，且对于特定的投掷群体而言，实际投掷铅球时其抛出点高度的差异基本不大，因此有理由相信铅球投掷人员的身高和臂长对铅球投掷距离的影响小于1 m。

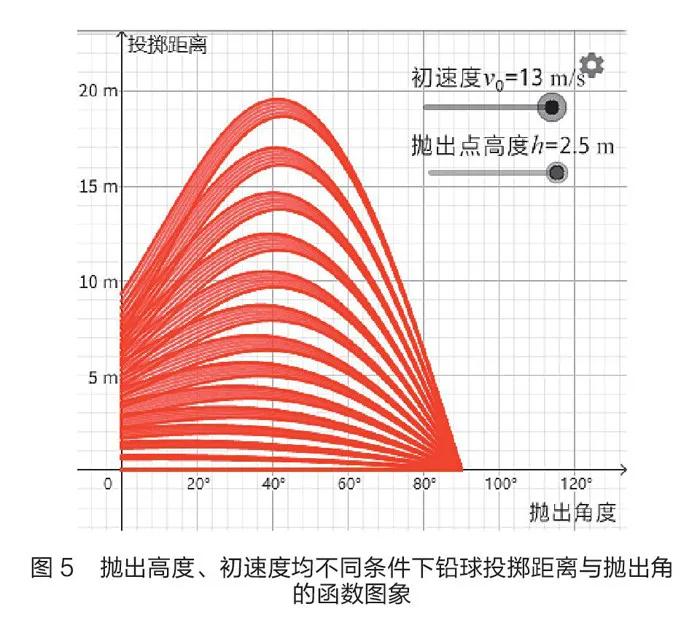
为了让以上结论更具说服力，笔者同时拖动与抛出点高度和初速度相应的滑动条，通过GeoGebra绘制一系列不同初速度且不同抛出高度下的投掷距离函数图象（如图5）。

在图5中，同一初速度、不同抛出高度的函数曲线集中在一起成带状分布，随着初速度增加，相应的“函数曲线带”依次向上排布，且在同一条“函数曲线带”中的各条函数曲线均随着抛出点高度的增加而依次从低到高分布。分别辨析图5中各条“函数曲线带”，发现在图4中分析得到的结论同样成立。

综合以上分析，学生得到以下启示：其一，为确保铅球的投掷距离最远，让铅球获得足够大的初速度是关键，这不仅需要运动员的自身强大机体力量作为根基，而且需要通过合理的加速方式提高铅球脱手时的初速度;其二，运动员在保证铅球获得最大初速度的基础上，应结合自身身高、臂长和投球姿势等因素确定铅球的抛出点高度，然后基于前面的初速度和抛出点高度决定自身专属的最优抛出角。

高中生投掷铅球初速度为5.6～8.2 m/s、铅球抛出点高度处于1.7～2.0 m^[2]。笔者借助GeoGebra通过函数图象读取得到相应的最优抛出角分布在33.7°（=5.6 m/s，=2.0 m）至39.3°（=8.2 m/s，=1.7 m）之间，铅球的最远投掷距离分布在4.8～8.39 m。对于不同个体条件下的具体最优抛出角，将相应数据输入GeoGebra中即可计算得到。

三、总结与展望

本案例中，笔者借助GeoGebra软件，以可视化分析的方式研究了铅球投掷距离的函数图象。师生通过研究发现：铅球的投掷距离受抛出角度和初速度影响较大，受抛出点高度影响较小。

为取得更好的投掷铅球成绩，运动员应意识到最佳抛出角的存在及其重要意义，还应该注意到最佳抛出角是随着铅球的初速度和抛出点高度的变化而动态变化的。运动员只有动态把握这些变化规律，才能在体育竞技中不断挑战自我。

运动员在投掷铅球时，可能还需要考虑空气阻力的影响。这有待今后进一步研究、完善。

需要强调的是，GeoGebra作为一款功能强大的动态分析软件，各种功能的应用无法穷举，未被文献记载的方法，唯有使用者在日常学习和生活中不断发掘，探索建立数学模型，并做可视化分析，才能在荆棘之路上一往无前。

参考文献

[1] 王倩，周华锋，刘茂辉，鲍伟.对两名不同水平男子铅球选手投掷技术的生物力学分析[J].北京体育大学学报，2007（3）：404-406.

[2] 卢飚，朱行建.推铅球出手角：高中生的视角[J].物理教师，2013（4）：55-56.

（作者系贵州省六盘水市民族中学高级教师）

责任编辑：祝元志