多轴伺服系统的非线性PID交叉耦合轮廓控制

盛贤君，路赛利，刘 宁

(大连理工大学电气工程学院，辽宁 大连 116024)

0 引言

在数控机床(CNC)加工中，多轴伺服系统高精度轮廓控制始终是研究热点[1-2]。数控机床实际运动过程中，由于控制系统不完全建模、动态特性不匹配及受到外部随机扰动等影响，导致加工过程中单轴伺服响应存在延时产生跟踪误差，实际曲线偏离理想参考曲线产生轮廓误差[3]。就多轴运动系统而言，轮廓轨迹由各轴协调运动完成，为了减小系统轮廓误差，提高单轴系统跟踪性能是重要前提，然而非线性加工曲线的轮廓误差并非各轴跟踪误差简单线性叠加，仅提高单轴跟踪精度并不能完全改善系统性能，需要引入交叉耦合轮廓控制器来提高系统运动精度[4]。

对于单轴系统位置控制，PID控制器简单且易于实现而被广泛应用于伺服系统，但该控制器参数确定后固定不变，将不能很好地反映出被控量与偏差之间的非线性关系[5-6]。罗和平等[7]提出用于伺服进给系统模糊PID控制算法，提高了系统的动静态性能，但模糊规则更多依赖于经验，不适合复杂工况场合；Wu J H等[8]将延时补偿器和滑模控制器应用于单轴伺服系统，改善了系统伺服性能，但控制器参数调整相对复杂。交叉耦合控制器(CCC,cross coupling controller)最早由Koren提出[9]，由单轴跟踪误差计算出轮廓误差，再进行解耦分配，有效解决了伺服轴动态性能不匹配的问题，但对非线性曲线而言，轮廓误差实时变化，传统交叉耦合控制往往达不到预期效果。Barton K L等[10]将迭代学习技术应用于CCC学习轮廓误差，从而修正控制信号和轮廓耦合增益，体现了自学习的特点，控制效果优良；金鸿雁等[11]采用互补滑模控制器与变增益交叉耦合控制器相结合的轮廓控制策略，互补滑模控制器提高了单轴跟踪精度，增强了系统的鲁棒性，但轮廓控制器采用传统动态补偿系数，可能会出现过补偿和欠补偿；吴飞等[12]从交叉耦合结构入手，设计了双轴变增益交叉耦合控制器，实现了轴间解耦，取得较好的控制效果，但对于曲率变化较大的曲线无法保证轮廓加工精度。

基于以上研究成果，本文提出一种基于交叉耦合结构的非线性PID(NLPID)轮廓控制器。单轴采用NLPID控制以提高系统的跟踪性能，避免了复杂的调参过程。此外，将NLPID应用于交叉耦合控制器并设计一种动态增益的轮廓误差补偿方法，实时估计系统轮廓误差后得到合适的补偿值，最后结合分配系数补偿到各轴，从而有效提高了系统的轮廓精度。

1 非线性PID控制器设计

传统PID控制器的参数为常数，而系统的动态过程是实时变化的，对于高精度运动系统，传统PID在控制能力和鲁棒性方面还有欠缺，往往不能得到优良的控制效果。NLPID控制器的参数随偏差变化，对于数控系统参数不匹配和扰动带来的非线性误差，能够很好地反映出系统的控制量和偏差之间的对应关系，从而达到更优的控制效果，其表达式如下：

(1)

式中，Kp(e(t))、Ki(e(t))及Kd(e(t))分别是比例、积分及微分参数，均为当前误差e的非线性函数。

通过分析传统PID参数随系统误差的理想变化关系，可以得出NLPID各参数随误差变化调整曲线如图1所示。

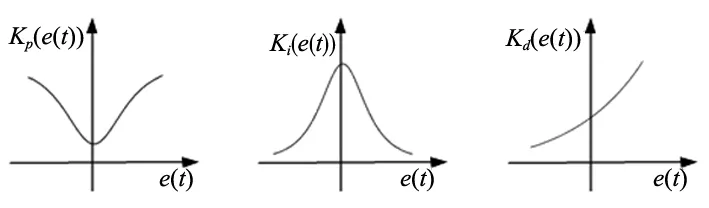
(a)Kp(e(t)) (b)Ki(e(t)) (c)Kd(e(t))图1 NLPID参数随误差变化曲线

(1)比例函数Kp(e(t))：比例控制主要用于加快系统的响应速度，属于有差调节，利用系统偏差进行相应的补偿。当系统偏差较大时，需要的补偿量越多，Kp的绝对值应该较大；反之，为防止补偿过度产生超调，Kp的绝对值应当较小，Kp(e(t))表达式如下：

(2)

(2)积分函数Ki(e(t))：积分控制属于无差调节，通过对偏差进行累积最后消除偏差。当系统误差较大时，为避免积分饱和，Ki应当较小；反之，为保证控制系统无静差，需要进行积分补偿，Ki应取较大的数值，表达式如下：

(3)

(3)微分函数Kd(e(t))：微分控制对偏差起到超前校正的作用，改善系统的响应速度和稳定性，Kd反应系统偏差的变化趋势，表达式为：

Kd(e(t))=ad+bdecde(t)

(4)

2 交叉耦合轮廓控制器设计

2.1 轮廓误差数学模型

轮廓误差ε(t)定义为由当前实际位置x(t)到理想轮廓曲线S的最短距离。

(5)

轮廓误差示意图如图2所示。

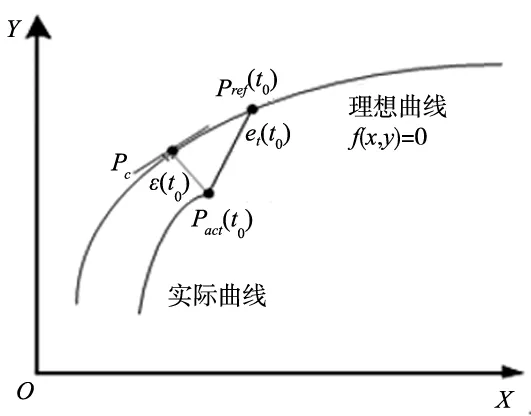
图2 轮廓误差示意图

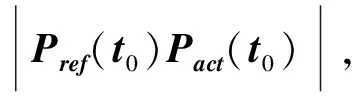
在数控系统中，插补方式多为直线插补和圆弧插补。直线或圆弧曲线的轮廓误差计算并不难，由平面几何关系可以快速得到，但对于任意阶数的非线性曲线，要实时得到轮廓误差精确值ε比较困难。因此，可采用参考运动轨迹局部近似的方法快速获得较为准确的轮廓误差估计值，在参考点Pref(t)处做内切圆，实际位置点Pact(t)到内切圆圆弧的最近距离εc作为系统轮廓误差估计值，如图3所示。

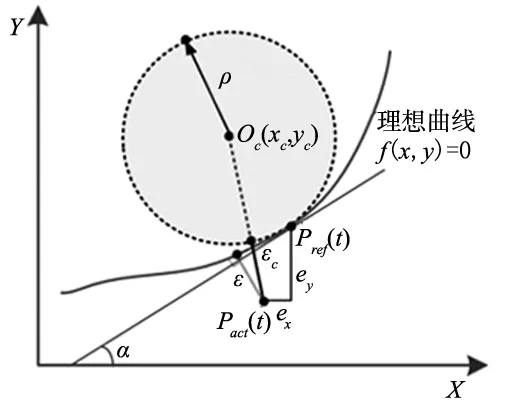
图3 平面非线性曲线轮廓误差

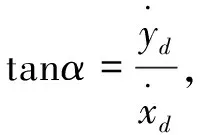
(6)

平台实际位置至内切圆圆弧的最近距离近似为轮廓误差估计值，即实际点Pact(t)到圆心Oc的距离减去内切圆半径，如图中εc所示，表达式为：

(7)

由平面几何关系，可以得出两点之间坐标关系与两轴跟踪误差和参考点切线倾角之间的数量关系如下：

xa-xc=ρsinα-ex

(8)

ya-yc=-ρcosα-ey

(9)

将式(8)和式(9)代入式(7)，得轮廓误差与两轴跟踪误差之间的关系如下：

(10)

对其进行二阶麦克劳林展开，得：

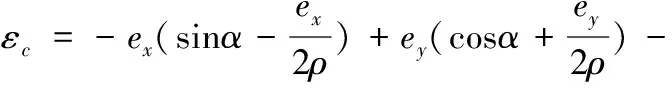
(11)

2.2 NLPID交叉耦合轮廓控制器

为了提高系统运动精度，仅减少单轴跟踪误差并不能满足要求，因此，双轴之间需要建立相应轴间联系。图4为双轴交叉耦合控制结构，由轮廓误差估计模型、协调控制器和误差分配模型组成，其原理为根据两轴参考位置和实际位置作为误差估计模型的输入值，建立两轴的耦合关系，将轮廓误差估计值作为协调控制器的输入得到轮廓误差补偿值，最后结合各轴的分配系数补偿至两轴以减小两轴跟踪误差和轴间轮廓误差。

根据两轴的跟踪误差结合式(11)，得到轮廓误差估计值εc，当内切圆半径远远大于两轴跟踪误差时，可忽略二次项，如式(12)所示：

(12)

得到分配系数Cx、Cy如式(13)所示：

(13)

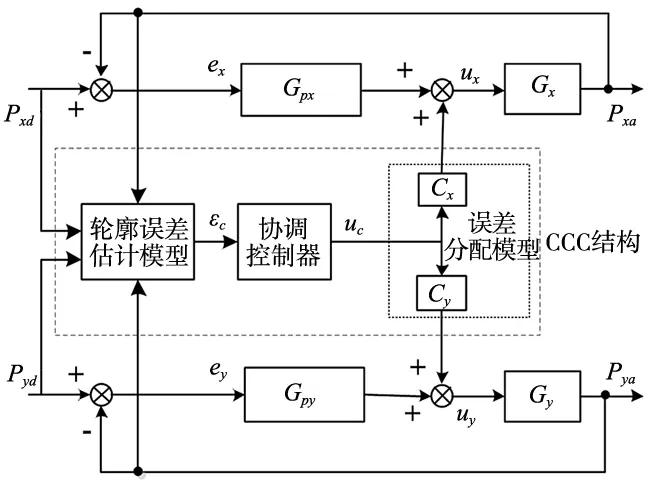
图4 交叉耦合控制结构框图

CCC的重点工作在于协调控制器设计，传统CCC的协调控制器为P控制器，结合分配系数按照一定比例补偿至两轴。对于非线性曲线而言，轮廓误差值实时变化，选择P控制器可能会出现过补偿或欠补偿，文献[12]所设计的变增益CCC选择PID控制器，对于曲率变化较大的曲线，补偿会出现波动。

为了更加准确地对轮廓误差进行补偿，得到较好的轮廓性能，Gpx、Gpy和协调控制器选择NLPID，对于轮廓误差的变化，协调控制器可得到合适的补偿值uc，结合分配系数补偿到各单轴。Pxd和Pyd是上位机输入的参考命令经由运动控器的插补算法得出，Gpx和Gpy是X、Y轴包括伺服驱动器、滚珠丝杠在内的数学模型，Pxd和Pyd为两轴位置检测装置输出的实际位置。

3 实验验证

3.1 实验平台

为了验证控制方法的有效性，进行双轴伺服系统轮廓控制实验。实验平台主要由X-Y运动机构、伺服系统和运动控制器组成，如图5所示。X、Y轴的有效行程分别为150 mm和100 mm，重复定位精度为0.001 mm；伺服系统为日本松下公司生产的MINAS A5 II系列；运动控制器采用美国GALIL公司生产的DMC-1846，通过PCI接口与上位机PC进行实时通信，最多可控制四轴联动，本平台仅使用两轴，图5中运动控制器在PC机内部，通过互联模块与伺服系统连接。

图5 实验平台

实验程序通过LabVIEW编写，给两轴发送参考位置命令后，通过读取两轴实时位置得到其跟踪误差，进而计算出实时轮廓误差补偿值，最后结合分配系数在下一时刻补偿至各轴。

3.2 实验结果对比及分析

实验中将无CCC和变增益CCC以及NLPID-CCC控制方法分别应用于控制器，对系统进行半径为3.75 mm圆轮廓轨迹规划，两轴分别输入频率为2π的余弦信号和正弦信号，表达式为：

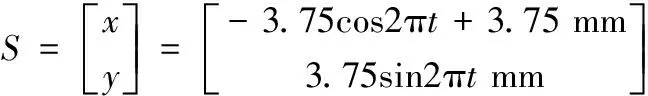
(14)

不同控制方法下的两轴跟踪误差经局部加权平均算法平滑处理后，如图6所示。

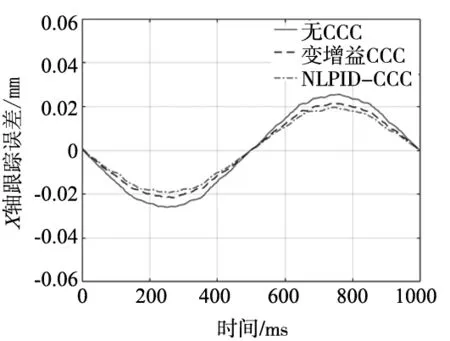
(a) X轴跟踪误差

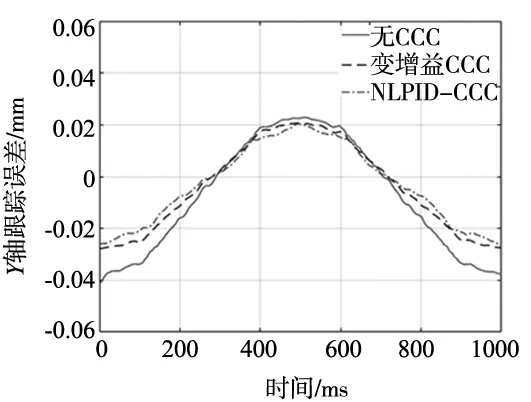
(b) Y轴跟踪误差图6 两轴的跟踪误差

可以看出，当系统开始运行时(t=0 ms)，两轴互相垂直，Y轴的跟踪误差较大。根据圆轮廓插补原理可知，此时Y轴的插补脉冲较多，故跟踪误差较大；经过四分之一周期后(t=250 ms)，X轴的插补脉冲增多，跟踪误差增大。相比于无CCC方法和变增益CCC方法，NLPID-CCC可有效提高单轴的控制性能，减小单轴系统的跟踪误差。

不同控制方法下的轮廓控制结果如图7所示，表1为轮廓误差典型值。

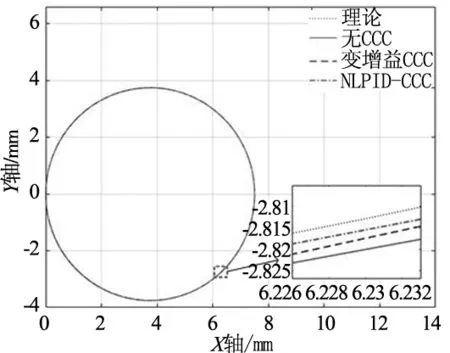
(a) 轮廓轨迹

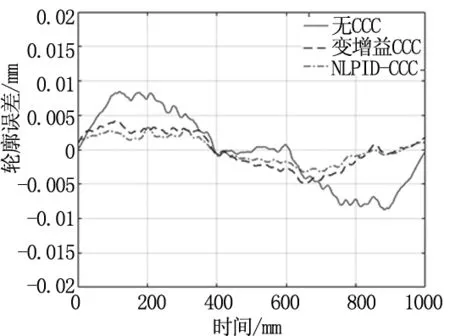
(b) 轮廓误差值图7 不同控制方法的轮廓控制结果

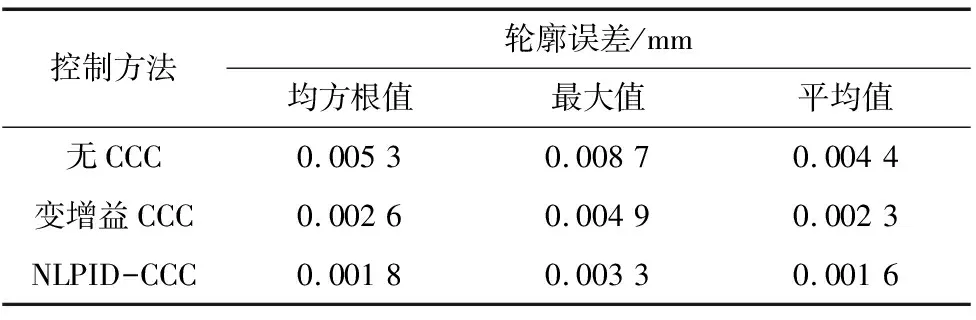
表1 轮廓误差实验结果

实验结果表明，相同实验条件下，采用CCC方法的轮廓效果明显优于无CCC方法，NLPID-CCC方法的轮廓控制效果最佳。由表1可知，相比于无CCC方法，NLPID-CCC方法在均方根值、最大值和平均值分别减少了66.04%、62.07%和63.64%；相比于变增益CCC方法，NLPID-CCC方法在均方根值、最大值和平均值分别减少了30.77%、32.65%和30.43%。因此，NLPID-CCC方法能够改善单轴跟踪精度，减小系统的轮廓误差，提高双轴系统的运动精度。

4 结论

本文在分析了NLPID控制器和多轴系统轮廓误差数学模型及交叉耦合的基础上，设计了基于NLPID的交叉耦合控制器。单轴NLPID位置控制可加快系统动态响应，提高跟踪能力，多轴间引入NLPID交叉耦合控制，实时估计轮廓误差后进行动态增益补偿。利用X-Y平台以典型的圆轮廓进行实验，通过结果对比，相比于变增益交叉耦合控制方法，在均方根值、最大值和平均值上有明显减小，NLPID-CCC能够有效地加快伺服轴动态响应，减小伺服系统的轮廓误差。本文所提出的交叉耦合轮廓控制器同样适用于高精度多轴运动系统，可提高其加工精度。