基于切削微元的盘铣刀铣削力预测研究*

孙兴伟，戚 朋，杨赫然，董祉序

(沈阳工业大学机械工程学院，沈阳 110870)

0 引言

螺杆钻具主要用与石油钻井中，其核心部件为螺杆马达，螺杆马达主要由定子和转子组成。针对转子的成形加工，现在普遍采用无瞬心包络铣削加工方法实现[1]。当铣削加工过程中铣削力波动较大时，容易造成过切或欠切现象，甚至还会导致刀片崩刃[2-3]。对螺杆曲面加工过程中的铣削力进行分析预测可以指导加工，以提高加工效率和工件表面质量。

铣削力预测模型有经验模型、解析模型、有限元模型和半解析模型等[4-5]。本文采用半解析模型对螺杆转子铣削力进行预测。该模型将机械加工物理模型中的刀具几何参数、工件材料性能和多物理场耦合效应等用切削力系数进行表征[6-7]。与理论解析模型相比，经验模型建模着重于计算加工过程中几何参数和切削参数的变化，通过切削力系数辨识标定试验，将切削力表示成上述一种或某几种参数的函数，然后运用回归分析方法进行系数求解。

魏俊立[8]基于刀具运动轨迹和铣削加工动力学特点计算了螺旋立铣刀的瞬时切厚与瞬时铣削力。Sa L等[9]基于刀齿真齿切削轨迹和加工表面几何形状，提出了多轴球头铣刀铣削时刀具工件啮合区域和瞬时未变形切屑厚度的解析模型，并据此建立了球头铣刀的铣削力模型。

本文基于加工过程中刀具轨迹的瞬时切削厚度模型建立盘铣刀的切削微元铣削力模型，并采用瞬时切削力辨识方法求解铣削力系数。二者结合可以更准确地反映出铣削力的在某一瞬时的特性。相对于简化切削轨迹和平均力系数辨识建模方法更能体现刀具切削刃局部铣削力的瞬时特征。

1 螺杆转子

螺杆转子成形加工所用设备为自主研制的专用螺杆数控铣床。为后文分析清晰，建立螺杆转子盘铣刀铣削的工件坐标系及刀具坐标系。其中工件坐标系为O-XYZ，刀具坐标系为o-xyz，如图1所示。图1中，盘铣刀的旋转运动为主切削运动，盘铣刀可沿Z轴及X轴分别完成轴向及径向进给运动，盘铣刀回转中心距螺杆中心的距离为h[10]。工件绕自身轴线的回转为C轴，为形成转子螺旋角，盘铣刀相对工件偏摆安装角β。加工时，X轴和C轴完成插补联动，盘铣刀一次加工过程包络铣削出螺杆转子的一个端向截面廓形。盘铣刀沿Z轴方向进给移动并重复上述包络铣削过程可加工出完整的螺杆转子廓形。螺杆工件坐标系O-XYZ和刀具坐标系o-xyz的转换关系式为：

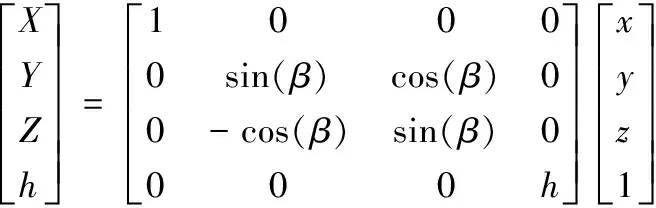
(1)

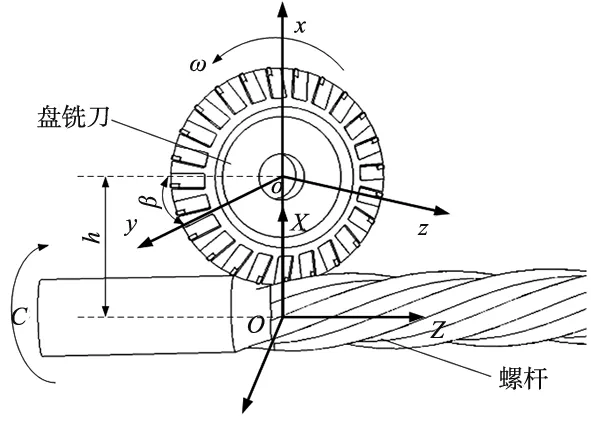
图1 包络铣削加工示意图

2 螺旋曲面铣削力模型

2.1 微元铣削力模型

在螺杆铣削加工过程中，由于盘铣刀的径向进给及工件的旋转运动，盘铣刀每齿的切削厚度在不断变化，从而使得切削力也在时刻变化。盘铣刀由多个相同刀片组成，因此切削过程为周期性断续切削，故只需研究一个刀齿在一次切削过程中的瞬时铣削力的变化即可确定切削过程中铣削力的变化。盘铣刀的铣削力建模采用半解析方法中的微元铣削力模型[9]，即将盘铣刀菱形刀片刀刃按几何型线离散成小的切削微元并建立微元力学模型，模型如式(2)，其中dFr,dFt,dFa分别为切削微元的径向力，切向力和轴向力。

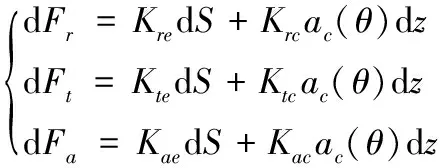
(2)

其中，Kte,Kre,Kae分别是切向、径向和轴向犁耕力系数，一般是只与刀具及工件材料有关的常数，单位为：N/mm；Ktc,Krc,Kac分别是切向、径向和轴向剪切力系数，一般与铣削加工切削参数有关，单位为：N/mm2，θ为切削刃瞬时位置角，ac(θ)为位置角θ的瞬时切削厚度，dS为切削刃微元弧长，dz为切削刃微元的切削宽度。微元铣削力建模方法为半经验模型法，铣削力系数需要辨识实验进行标定。具体流程如下：首先，根据刀具和工件的几何关系并结合加工参数确定铣削力模型；其次，对切削加工过程进行分析并建立瞬时切削厚度模型，并确定切入切出角和微元积分的上下限；最后，结合铣削力测量实验并采用瞬时铣削力系数辨识方法对系数进行辨识求解。

2.2 瞬时切削厚度模型

在加工过程中，瞬时切削厚度ac(θ)随切削刃的位置角θ的变化而变化，瞬时切削厚度可用在同一切削角度下的前一刀齿轨迹和当前刀齿轨迹的距离来表示。由于存在进给运动，切削刃所扫掠过的轨迹为摆线。切削刃瞬时切削厚度示意图如图2所示。根据实际加工过程并结合示意图分析可知线段EG的长度即为实际加工中的瞬时切削厚度[12]。根据瞬时切削厚度示意图的几何关系可得出线段EG的长度为：

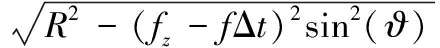
(3)

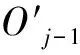
(4)

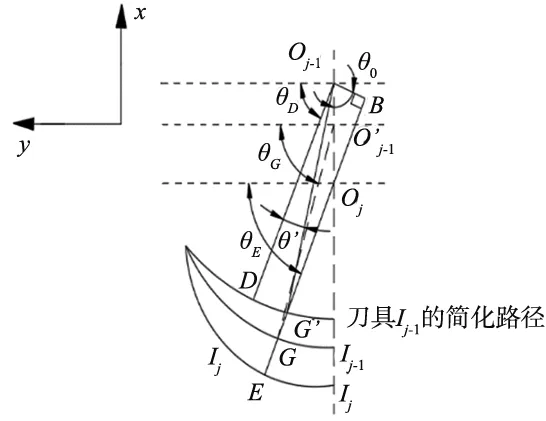
图2 瞬时切削厚度示意图

2.3 切削刃微元受力分析

对盘铣刀上的菱形刀片的形状进行分析可知，切削刀刃由直线刃和圆弧刃组成，由于稳定切削状态下主要是圆弧刃参与切削，因此选择沿刀刃型线进行微分进而得到微元切削刃，对切削微元沿着圆弧刃进行积分即可求出相应圆弧刃弧长上的瞬时铣削力。对微元切削刃进行受力分析，如图3所示，λ为刀片安装偏角，φ为某一切削微元的位置角。

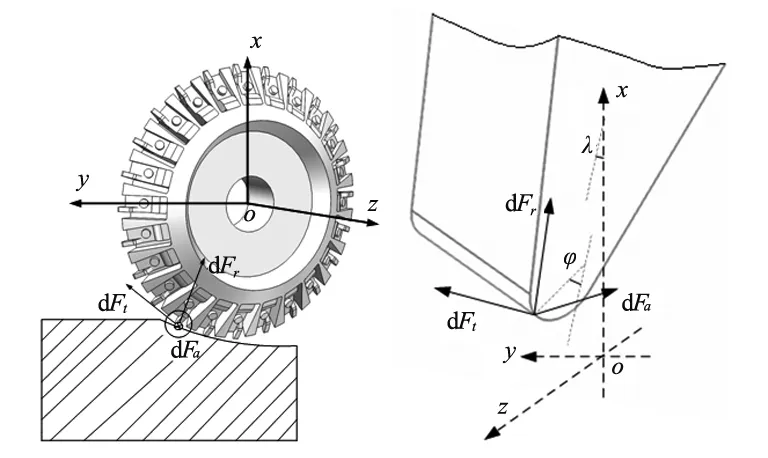
(a) 切削示意图 (b) 切削微元受力分析图3 切削刃微元受力分析示意图

由于微元位置角φ的存在，所以需要将切向力、轴向力和径向力投影到刀具坐标系o-xyz上并表述。如式(5)所示，其中T为变换矩阵，矩阵如式(6)所示。

(5)

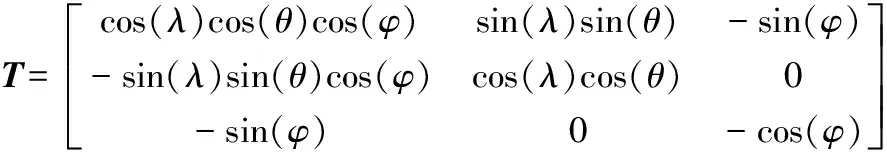
(6)

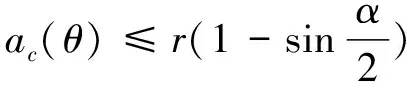
dS=r·dφ

(7)

dz=r·sinφdφ

(8)

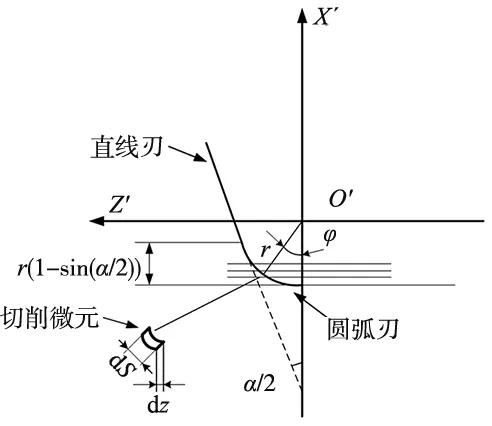
图4 切削刃微元示意图

2.4 瞬时切削力模型

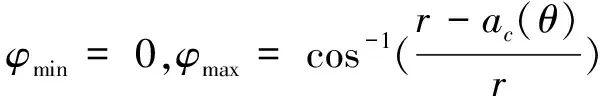
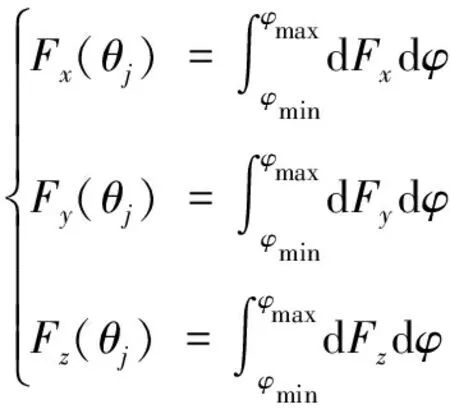
(9)

综合式(1)、式(3)～式(9)，可得出在刀具坐标系o-xyz上x,y,z三个方向的瞬时铣削力如式(10)：

(10)

其中，式(10)中A1,A2,A3,A4和φ分别为：

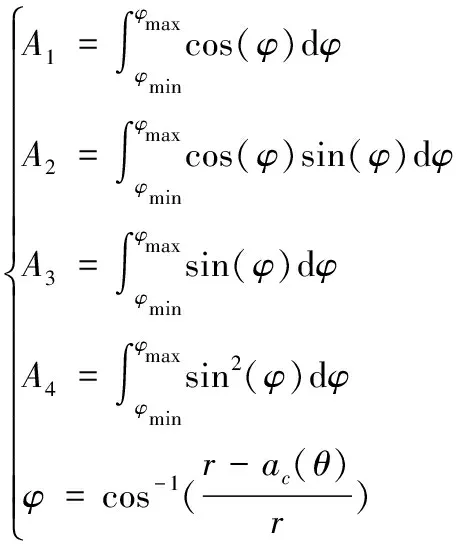
(11)

工件坐标系上O-XYZ的三个方向上的瞬时切削力方程如式(12)：

(12)

3 铣削力系数辨识及实验验证

3.1 铣削力系数辨识方法

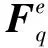
(13)

K=[KreKteKaeKrcKtcKac]T

由式(10)可知，一个切削时刻对应一个瞬时切削厚度，可构成3个方程，但是有6个系数，所以上述方程组属于不定方程组。因此为了求解6个铣削力系数，需对一次切削过程按时间进行离散，取两个或多个时间点进行联立求解，为简化计算，遂在此取一个切削过程的两个时刻来进行计算，如式(14)。

(14)

3.2 铣削力系数辨识实验

为验证铣削力系数辨识方法的正确性和铣削力模型的准确性，可根据辨识方法设计相应实验方案，并进行盘铣刀加工五头螺杆的铣削实验。五头螺杆材料为45钢，菱形刀片材料为40Cr，型号为VBMT160412，刀片参数如表1所示，实验所加工五头螺杆转子的参数如表2所示。

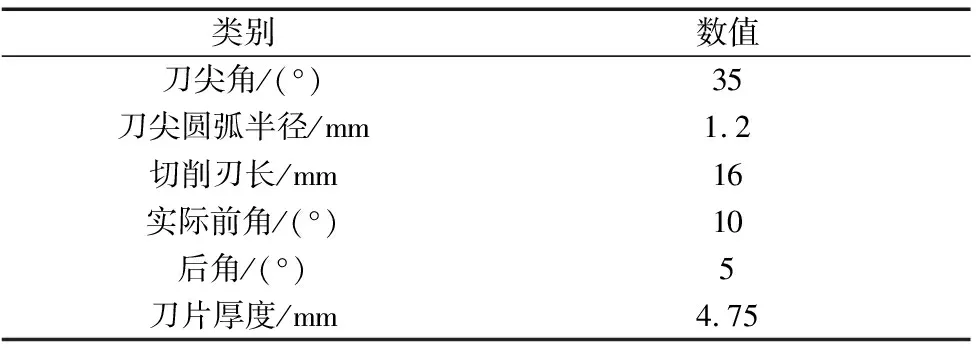
表1 菱形刀片参数

表2 五头螺杆转子参数

图5 铣削力测量实验装置

在专用螺杆铣床LXK-300G上进行实验，通过MUCHEN-MC3D160三分力传感器测量铣削力，数据采集卡为三通道的MCD-3USB，铣削力的采样频率范围为500～5000 Hz。传感器量程为50 kN，可测XYZ三个方向上的铣削力，测力实验装置如图5所示。根据实验目的设计正交实验方案，相应测力实验所得数据进行求解得到对应的Kte,Kre,Kae,Ktc,Krc,Kac，数值如表3所示。铣削力系数所对应的A组加工参数为：转速180 r/min，间歇进给量2 mm,加工倍率20%；B组加工参数为：转速162 r/min，间歇进给量2 mm,加工倍率为10%。

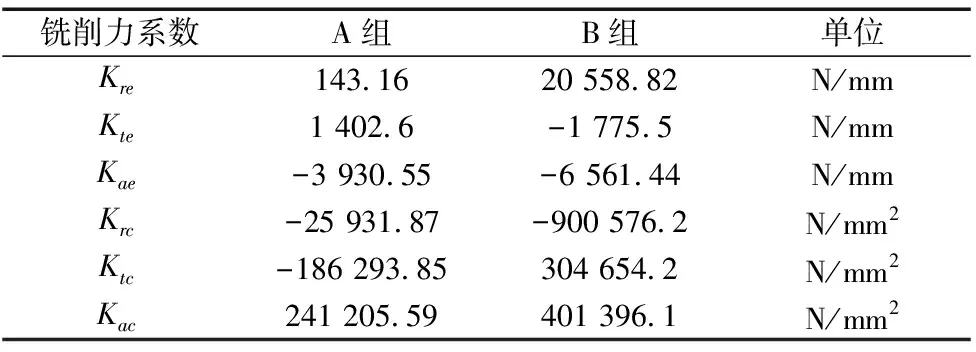
表3 铣削力系数

将通过实验辨识得到的铣削力系数代入铣削力模型式(12)中，针对单次切削过程绘制铣削力仿真图形和实测力对比如图6所示。图6a为A组加工参数下的铣削力对比图。图6b为B组加工参数下铣削力对比图。Fx1、Fy1、Fz1为测得结果，Fx、Fy、Fz为预测值。

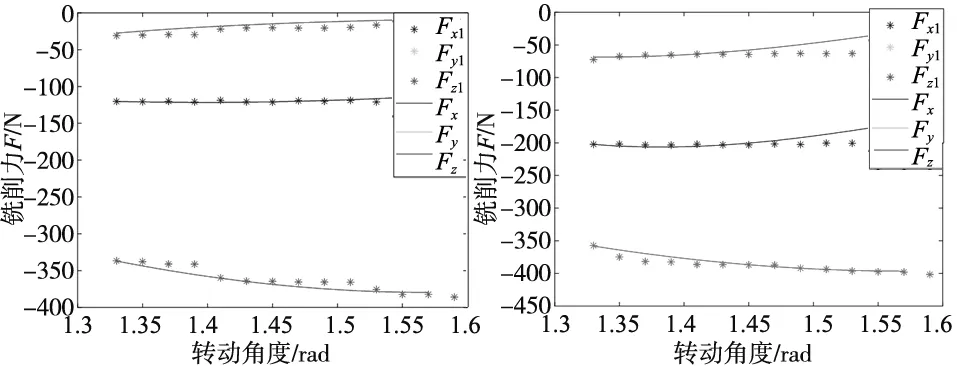
(a) A组参数铣削力对比图 (b) B组参数铣削力对比图图6 实测力与预测力

由图6可知，测量过程中由于受到铣削力测量系统精度及刀盘、工件的加工与装配等因素影响，铣削力仿真数值与实测值存在一定偏差，但偏差数值尚在允许范围内，且仿真结果与实测结果的趋势相同。

4 结论

本文基于切削微元建立了螺杆转子铣削力半解析预测模型。并结合瞬时铣削力系数和平均铣削力系数辨识方法提出了基于瞬时切削微元和加工参数的铣削力系数辨识方法。

通过辨识实验求解出铣削力系数，并对铣削力的预测值与实测值进行了比较分析。分析结果表明：本文建立的预测模型能够准确预测盘铣刀加工过程中的铣削力，从而验证本文提出方法的正确性与实用性。