基于跳距修正的WSNs的无线传感网络节点定位算法*
2021-12-29陈卡
陈 卡
(驻马店职业技术学院公共教学部,河南 驻马店 463000)
0 引言
随着电子信息技术的发展以及电子元器件成本的下降,由价格低廉的传感节点构成的无线传感网络(Wireless Sensor Networks,WSNs)[1-2]已在军事勘察、康复医疗、智能农业方面得到广泛应用[3]。准确地获取节点位置信息有助于提高应用效率。因此,估计节点位置成为WSNs领域的研究热点。
现存的关于WSNs的定位算法可分为基于测距和非测距两类定位算法。测距定位算法需要测量未知节点与锚节点间的距离,并且测距精度与定位精度密切相关。而非测距定位算法是通过网络拓扑的连通信息估计未知节点位置,定位精度受网络拓扑影响[4]。相比于测距定位算法,非测距定位算法成本较低。从成本角度,非测距定位算法更适用于WSNs。
DV-Hop算法属经典的非测距定位算法[5],一直受到较大的关注。尽管DV-Hop算法的复杂性低,但是其存在一些不足,如最小跳数估计不准,跳距估计误差大。为此,研究人员提出不同的改进策略。
任克强等[6]利用节点偏差系数对跳数估计值进行修正,并利用最小均方误差优化平均跳距。尽管该算法对跳数和跳距进行了修正,但是这只是提升了测距精度,并没有对定位算法进行优化。测距只是定位算法的基础。黄文永等[7]利用锚节点密度对每跳距离进行修正,并利用锚节点坐标以及密度对节点位置进行校正,但是该算法要求高密度的锚节点。Cui L Z等[8]为了降低跳数估计的误差,将离散的跳数转化为连续值,再搜索节点位置的最优解。尽管该算法能够获取高的定位精度,但是算法的复杂度很高,并不适合于低成本的WSNs网络环境。
为此,综合现有的文献,本文先分析了导致DV-Hop算法定位精度不高的原因,再基于跳距修正的节点定位算法(Hop Distance-Corrected Localization,HDCL)。主要的工作归纳如下:①对估计节点位置的锚节点进行筛选,避免因锚节点共线而出现定位盲区。现存的多数定位算法并没有锚节点的选择问题;②采用无偏估计对跳距进行优化处理,降低跳距估计误差;③获取测距数据后,再利用Jaya算法搜索节点位置,并对搜索的区域进行约束,提高搜索精度。
1 DV-Hop定位算法
DV-Hop定位算法主要由以下三个阶段构成[9]:
1.1 最小跳数的估算阶段
网络内所有锚节点在网络内广播分组包Packet,其包含锚节点的位置以及Packet被传递的跳数Num_Hop。节点接收了分组包Packet后,先判断是否首次接收该分组包。若是首次,就保存相关信息,再将Num_Hop+1,并向邻居节点传递此分组包。若不是首次,就将当前获取的跳数值与存储的跳数值进行比较,保存最小的跳数值。通过分组包Packet的传递,使网络内节点获取到锚节点的最小跳数值。
1.2 跳距的估算阶段
依据第一阶段所获取的最小跳数值,锚节点先估计与其他锚节点间的平均每一跳的距离(简称平均跳距):
(1)
式中,Hopsizei表示锚节点i所估计的平均跳距;dij表示锚节点i与锚节点j间的真实距离;Num_Hopij表示锚节点i与锚节点j间的最小跳数。
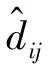
(2)
1.3 节点位置估计
未知节点获取了到锚节点的估计距离后,便通过最大似然法估计未知节点的位置。
由于WSNs网络拓扑结构的不规则性,锚节点和未知节点的分布并不均匀,只利用跳数与跳距的乘积作为估计距离存在较大误差。为此,HDCL算法从跳数、跳距和锚节点的分布角度对DV-Hop算法进行改进,进而提高定位精度。
2 HDCL定位算法
考虑二维(2D)网络区域为l1×l2。n个未知节点,其位置坐标为θi=[xi,yi]T,且θ∈R2。通过锚节点估计未知节点的位置。令αk=[xk,yk]T表示第k个锚节点的位置,且k=1,2,…,m。
2.1 基于无偏估计的平均跳距的修正
直接利用式(1)计算平均跳距存在较大误差。为此,HDCL算法引用无偏估计对其进行修正[10]。先建立跳距误差函数。考虑式(1)的差值,再对两者间的差值进行平方运算:
(3)
采用无偏估计。为了获取最小误差,对式(3)进行求导,并令求导后的等式为0:
(4)
再依据式(4)重新计算锚节点i的平均跳距:
(5)
2.2 基于共线度的锚节点的筛选
在估计节点位置时,需选择3个锚节点,并建立相应的距离方程。然而,如果所选择的3个锚节点位于同一条直线,即共线,就无法估计节点位置,出现定位盲区[11]。
令Ni={a1,a2,a3}表示未知节点i所选择的3个锚节点。先计算由这3个锚节点所形成的三角形的内角的余弦值:
(6)
式中,d12、d13和d23分别表示锚节点a1与a2的距离、a1与a3距离和a2与a3距离。若αi=π,cosαi=-1时,其表明未知节点i所选择的3个锚节点{a1,a2,a3}共线。若αi=π/3,cosαi=1/2时,则未知节点i离3个锚节点{a1,a2,a3}距离相等。利用这3个锚节点估计未知节点位置误差最小。
因此,将cosαi作为共线度。未知节点利用共线度筛选锚节点。将共线度在0~0.5范围内的锚节点集作为自己用于定位的锚节点。筛选锚节点的步骤如下:
(1)先从邻居锚节点选择三个锚节点,再依据式(6)计算所选择的三个锚节点的共线度;
(2) 判断共线度是否在0~0.5范围。若不在此范围内,就重新选择。返回到式(1)。
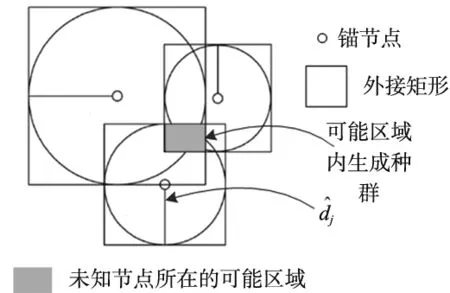
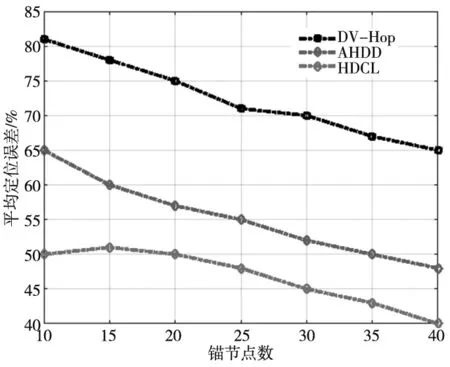
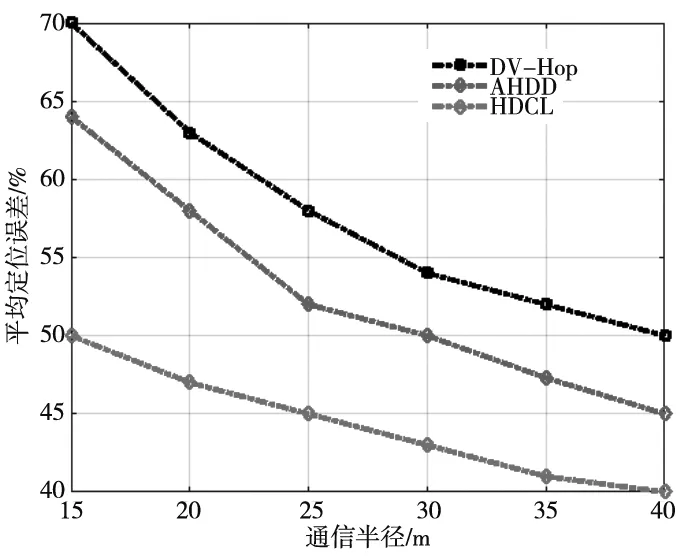
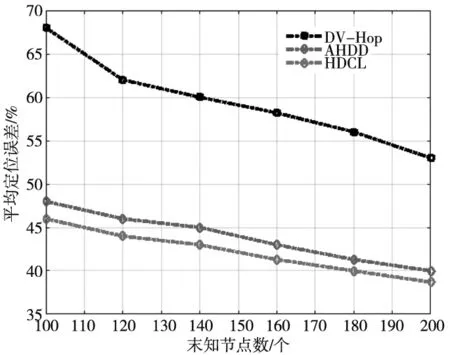
以图1为例,分析基于共线度的锚节点筛选过程。图中A1、A2、A3和A4为锚节点,B1为未知节点。B1先选择离自己较近的3个锚节点{A1,A2,A3},再依式(6)计算共线度cosα1。接下来,判断是否满足0 图1 基于共线度的锚节点筛选 HDCL算法将Jaya算法[12]引入定位阶段。Jaya算法具有较快的收敛性能。将估计节点位置转换成目标优化问题,即以定位误差构建目标函数。 (7) 未知节点先通过修正后的最小跳数以及优化后的跳距后,计算离锚节点的距离。然后,以锚节点位置为圆心以估计的距离为半径形成圆的外接正方形。最后,以三个外接正方形所重叠的区域表示未知节点的可能区域,如图2所示。 图2 种群的可行区域 再在图2所示的可能区域内随机生成种群。为了提高定位精度,种群依据式(8)的上、下界搜索未知节点位置: (8) 算法1给出定位的具体步骤,如表1所示。 表1 HDLC算法的定位步骤 利用MATLAB建立仿真平台,分析HDCL算法的定位性能。在100 m×100 m区域内随机部署n个未知节点和m个锚节点。所有节点的通信半径相同,且为R。具体的仿真参数如表2所示。 表2 仿真参数 选择经典的DV-Hop算法,胡玉兰等[13]提出基于平均跳距优化的DV-Hop改进算法(Average Hop Distance Optimal DV-Hop,AHDD)作为参照,对比分析它们归一化平均定位误差: (9) 首先分析锚节点数对平均定位误差的影响,如图3所示,其中锚节点数从10~40变化,通信半径为30 m,未知节点数为100。 图3 锚节点数对平均定位误差的影响 从图3可知,锚节点数的增加减少了平均定位误差,提高定位精度。原因在于:锚节点数越多,未知节点能够获取的测距信息越多,越能够筛选有利的锚节点集。但是,DV-Hop算法,AHDD和HDCL算法的平均定位误差随锚节点的变化情况并非相同。当锚节点数小于15时,HDCL算法的平均定位误差比AHDD算法的平均定位误差下降了约12.5%~13%;当锚节点数大于35时,HDCL算法的平均定位误差比AHDD算法的平均定位误差下降了约2.2%~3.6%。这说明,在锚节点较少时,HDCL算法在平均定位误差性能优势更明显。原因在于:在锚节点较少时,AHDD和DV-Hop算法的平均跳数和跳距误差更大。 最后,分析通信半径R对定位精度的影响。本次实验参数:未知节点数n=100;锚节点数为20个;通信半径从15 m~40 m变化。 图4给出DV-Hop算法、AHDD算法和HDCL算法的平均定位误差随通信半径R的变化情况。 图4 节点数对平均定位误差的影响 可以看出,通信半径的增加有利于降低平均定位误差。原因在于:通信半径越大,节点通信的范围越大,能够获取的定位信息越多,这有利于提高定位精度。此外,相比于DV-Hop算法和AHDD算法,HDCL算法降低了平均定位误差。在通信半径较低时,HDCL算法在平均定位误差性能方面的优势更明显。 最后,分析未知节点数对平均定位误差的影响,如图5所示。未知节点数从100~200变化,通信半径为40 m,锚节点数占未知节点数的比例为30%。例如,当节点数200时,锚节点数为60个。 图5 未知节点数对平均定位误差的影响 可以看出,平均定位误差随未知节点数的增加呈缓慢下降,变化较稳定。相比于AHDD和DV-Hop算法,提出的HDCL算法有效地降低了平均定位误差。这归功于:HDCL算法通过跳距和跳数的优化,并利用共线度筛选锚节点,避免共线问题,提高了定位精度。 针对传统的DV-Hop算法的定位误差,本文分析产生误差的原因,并提出基于跳距修正的节点定位算法HDCL。HDCL算法通过无偏估计修正跳距,并考虑到参与估计未知节点位置的锚节点的共线问题,通过共线度概念选择适宜的锚节点。最后,利用Jaya算法估计节点位置。仿真结果表明,相比于DV-Hop算法和AHDD算法,HDCL算法降低了定位误差。后期研究如何进一步减少在估计跳数和跳距阶段所累积的误差,提升定位精度,这将是后续研究的重点方向。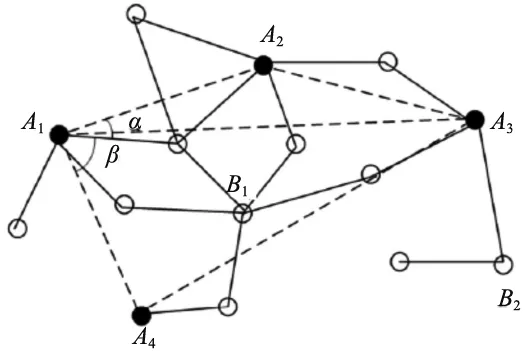
2.3 基于Jaya算法的节点位置估计
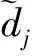
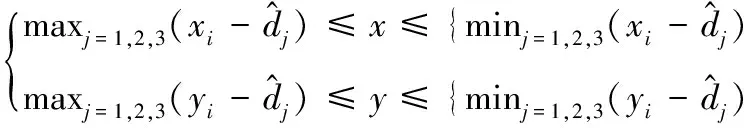
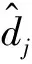
2.4 定位步骤

3 仿真与分析
3.1 仿真环境

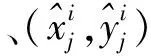
3.2 锚节点数对平均定位误差的影响
3.3 通信半径对平均定位误差的影响
3.4 未知节点数对平均定位误差的影响
4 总结
